利用弯曲晶体实现空间带电粒子屏蔽方法及应用初探
2019-04-25李衍存贾晓宇郝志华向宏文秦珊珊盛丽艳
李衍存,贾晓宇,郝志华,向宏文,秦珊珊,张 弘,王 颖,盛丽艳
(北京空间飞行器总体设计部,北京 100094)
0 引言
传统的空间辐射粒子屏蔽技术利用的是带电粒子在物质中的能量损失原理,屏蔽体厚度越大,能量损失越大,因此需要质量较大的屏蔽体,会额外增加航天器质量。
1976年,Tsyganov[1-2]首先提出了利用弯曲晶体进行粒子偏转的方法:当粒子入射到晶体中时,由于沟道效应,在合适的条件下,粒子被束缚到晶体沟道中;当晶体发生弯曲时,束缚在晶体中的粒子随着晶体弯曲实现偏转。Tsyganov于1976年在10 GeV加速器上对该偏转方法进行了试验验证[3],将8.4 GeV质子入射到不同弯曲角度的硅晶体中,最终得到出射粒子数在与晶体弯曲角度相同的方向上出现峰值,证实了弯曲晶体对粒子具有偏转效果。目前,弯曲晶体对粒子偏转效应主要应用于加速器领域中实现对加速器粒子的引出,已形成了比较成熟的理论[4],并在俄罗斯IHEP的 70 GeV质子加速器(U-70)上得到了实际应用[5]。随着碳纳米管材料的发现,碳纳米管的规则结构与内部规则势场也可起到与硅晶体类似的对带电粒子的束缚与偏转作用[6-9],且碳纳米管内部势垒大于硅晶体势垒[10],对带电粒子束缚与偏转效果比硅晶体好,是目前的研究热点。与硅晶体成熟理论方法不同,碳纳米管的研究还处于仿真模拟阶段。
本文基于国际前沿的理论成果,将弯曲晶体偏转带电粒子的方法应用到空间带电粒子屏蔽中,尝试一种新的空间带电粒子屏蔽方法。
1 弯曲晶体对带电粒子偏转机理与关键参数
1.1 偏转机理
晶体内部规则的点阵结构会形成规则的势场,带电粒子沿着晶体特定的晶面入射时,两侧的晶面会形成连续的势垒[11],如图1所示。带电粒子以较小的角度沿轴线入射晶面时,粒子动能的横向分量小于晶面势垒,则可被束缚在势垒中,沿着晶面轴向运动,形成沟道效应,如图2所示。晶体发生弯曲时,束缚在其中的带电粒子会随之发生偏转,如图3所示。图1给出的是晶体对于正带电粒子形成的势垒,对于负带电粒子形成的势垒是相反的,对正带电粒子产生排斥的区域,是对负带电粒子产生束缚的区域,因此弯曲晶体可实现对正负带电粒子的偏转。地球辐射带中同时存在电子和质子,弯曲晶体可实现对地球辐射带粒子的偏转。
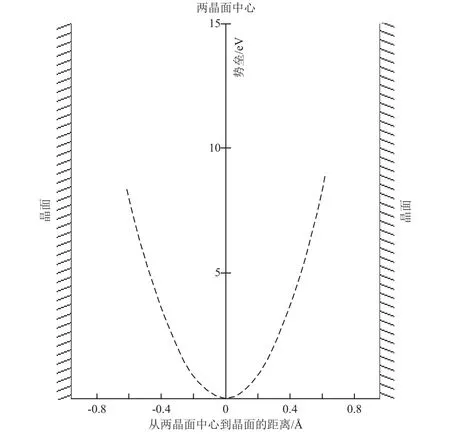
图1 硅(110)晶面对质子形成的沟道势垒Fig. 1 Continuum potential energy for protons channeled in the (110) planes of Si

图2 带电粒子在晶体中的运动示意Fig. 2 Diagram of a charged particle passing through a crystal
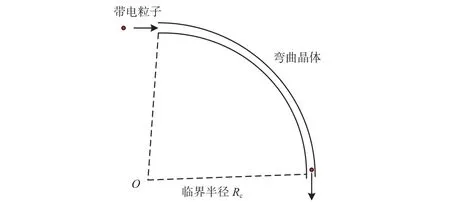
图3 带电粒子在弯曲晶体中发生偏转示意Fig. 3 Diagram of a charged particle deflected by bent crystal
1.2 偏转关键参数
对于直晶体,带电粒子入射到晶体中,入射角度必须符合一定的条件才可被捕获到沟道中,该角度称为临界角。由于临界角的存在,当晶体发生弯曲时,弯曲半径必须符合一定的条件,带电粒子才可被捕获在沟道中,该半径称为临界半径。带电粒子被捕获到沟道中、运动一段距离后,存在一定的概率退出沟道效应,该距离称为退沟道长度。由于退沟道效应,粒子只有一定的比例会发生预期的偏转,该比例称为偏转效率。从空间带电粒子防护的角度,希望实现较大的偏转效率以达到较好的防护效果。偏转效率受到临界角、临界半径、退沟道长度等因素影响,下面将针对这些参数进行分析。
1)临界角
参考图2所示的带电粒子在晶体中的运动,带电粒子入射到晶体中时,入射方向与晶体轴方向存在一定夹角,当入射夹角小于临界角ψc时,带电粒子动能的横向分量小于晶面势垒,则可以被束缚在晶体沟道中;当入射夹角大于临界角ψc时,带电粒子则无法被捕获到晶体沟道中。ψc的计算公式[6, 9]为
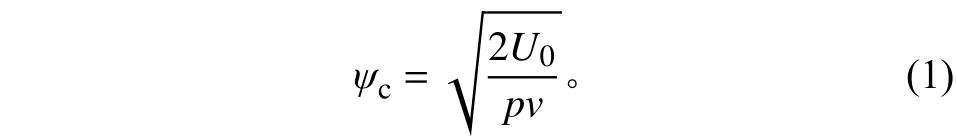
其中:对于硅晶体,U0代表两个晶面之间的势垒,常用的(110)晶面,U0=22.7 eV[6];对于碳纳米管,U0代表粒子在碳纳米管中的势垒,约取为60 eV[7];p是带电粒子动量;v是带电粒子速度。
2)临界半径
与临界角相对应,当带电粒子沿晶面轴向入射到弯曲晶体中时,晶体弯曲半径大于临界半径Rc时,带电粒子可被捕获在晶体沟道中;晶体弯曲半径小于临界半径Rc时,带电粒子无法被捕获到晶体沟道中。Rc的计算公式[8]为

其中:d是晶体势垒宽度,对于硅晶体为两个晶面间距,0.23 nm;对于碳纳米管,d可近似取C–C键长,0.142 nm。
3)退沟道长度
带电粒子在晶体沟道中运动时,不会无限持续下去,经过一定距离后,由于与晶格原子碰撞等原因,带电粒子能量的横向分量会发生变化,若横向分量超出势垒高度,则粒子会退出沟道。带电粒子运动一定距离后,存在1/e的可能会退出沟道,该长度称为退沟道长度LD。
硅晶体的退沟道长度为[9]

式中:Z1是入射粒子电荷;LC是库仑对数,LC=,其中me为电子质量,I为靶原子电子平均激发能,硅原子I=173 eV,碳原子I=81 eV;aS是屏蔽距离,,其中Z2为靶原子电荷,aB为玻耳半径,aB=5.29×1011m,电子和质子入射到硅晶体中时,Z1=1,Z2=14,aS=1.66×1011m;dp是弯曲晶体晶面间距,硅晶体dp=0.23 nm;re是经典电子半径,re=2.82×10-15m;c为真空中的光速。
碳纳米管的退沟道长度[9]为
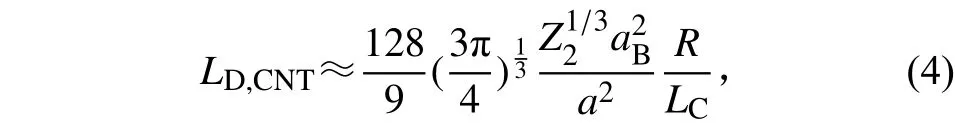
其中:Z2、aB、LC含义同式 (3);a是 C–C键长,0.142 nm;R是碳纳米管弯曲半径。
4)偏转效率
带电粒子在弯曲半径为R的晶体中运动,由于退沟道效应影响,只有一部分粒子最终成功实现偏转,当入射粒子在临界角范围内时,被偏转的粒子数量与入射粒子数量的比值为偏转效率Pd。其计算公式[6]为

式中:Pc代表捕获概率,Pc=1−Rc/R;α是晶体弯曲角度;Ld是弯曲晶体中的退沟道长度,Ld=LD·(1−Rc/R)2,其中LD为直晶体中的退沟道长度。
2 硅晶体和碳纳米管对地球辐射带电子和质子偏转效果分析
2.1 偏转参数的计算
地球辐射带中的带电粒子主要是电子和质子,这2种粒子是造成空间电离总剂量损伤、位移损伤等辐射效应的根源,针对这2种粒子进行屏蔽,可有效降低航天器受到的辐射损伤。目前航天器空间环境设计中,常用的地球辐射带模型是AE8(电子模型)和AP8(质子模型),模型中电子能量范围为0.04 ~7 MeV,质子能量范围为0.1~400 MeV[12]。下面针对辐射带中的电子和质子,进行临界角、临界半径、退沟道长度和偏转效率4个参数分析。
1)临界角
根据式(1)可以计算得到地球辐射带中不同能量的电子和质子入射硅晶体和碳纳米管的临界角,如图4所示。
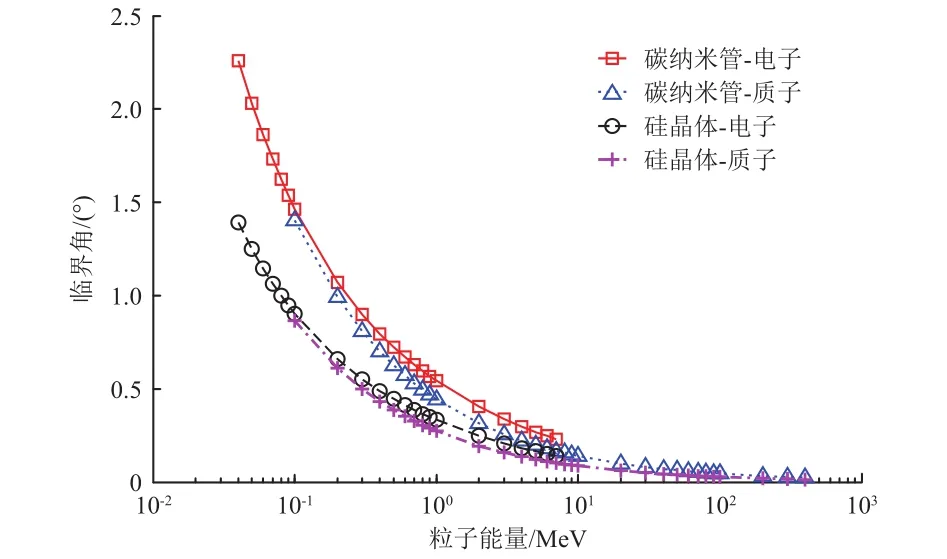
图4 空间带电粒子入射硅晶体和碳纳米管的临界角Fig. 4 Critical angles of space electrons and protons of different energies
在晶体势垒一定的条件下,粒子的入射角度必须足够小,才能保证粒子动能的横向分量小于晶体势垒,从而被捕获到沟道中。图4中的地球辐射带电子的临界角为2.3°~0.3°,质子的临界角为1.4°~0.02°。这2个临界角都非常小,意味着空间带电粒子必须以接近平行于晶体轴向入射,才可被晶体捕获。
由图4可见,电子与质子的临界角接近,电子临界角略大于质子临界角。一方面,临界角与入射粒子动量和速度乘积的平方根成反比,在电子和质子动能相同的情况下,粒子动量和速度乘积接近,因此两者临界角接近。另一方面,根据粒子在相对论条件下的动能、动量和速度的关系,可以得到粒子动量和速度的乘积的计算公式为
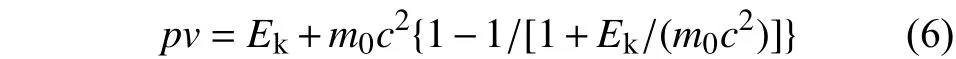
其中:Ek为粒子动能;m0为粒子静止质量。在动能Ek相同的条件下,电子动量和速度的乘积略小于质子,因此电子的临界角略大于质子临界角,这意味着晶体对电子的捕获能力要强,相应对电子的偏转效率要高于对质子的。对高轨航天器,电离总剂量来源于空间电子,晶体对电子的高捕获能力有利于降低总剂量效应。
2)临界半径
根据式(2)可以计算得到地球辐射带中不同能量的电子和质子入射硅晶体和碳纳米管的临界半径,如图5所示。
当晶体发生弯曲时,在晶体势垒一定的条件下,入射粒子能量必须达到一定值,临界半径也必须足够大,才能保证粒子能量的横向分量小于晶体势垒,从而被捕获到沟道中。从图5可以看到,对于0.04~7 MeV的电子,其临界半径范围为91 nm~9 μm,对于0.1~400 MeV的质子,临界半径范围为24 μm~0.8 mm,能量低于100 MeV时,临界半径在μm量级,能量超过100 MeV后,临界半径达到mm量级。

图5 空间带电粒子入射硅晶体和碳纳米管的临界半径Fig. 5 Critical radius of space electrons and protons of different energies
由图5可见,在能量相同的情况下,质子临界半径略大于电子临界半径。这意味着捕获相同能量的粒子,质子需要更大弯曲半径的晶体。换言之,对于某弯曲半径确定的晶体,可捕获电子的情况下,可能无法捕获质子,即对质子的捕获效率低。
3)退沟道长度
根据式(3)和式(4),可以计算得到地球辐射带中不同能量的电子和质子入射硅晶体和碳纳米管的退沟道长度,如图6所示。
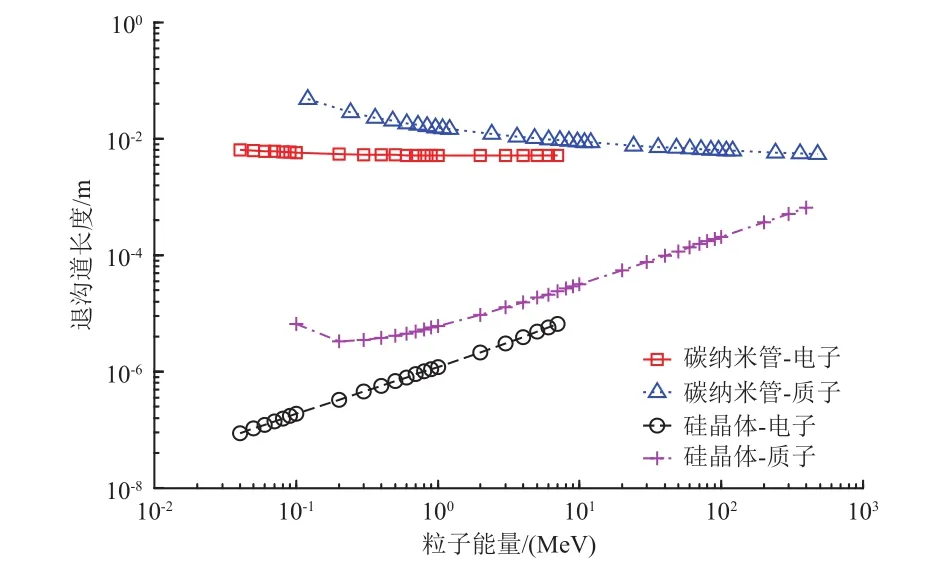
图6 空间带电粒子入射硅晶体和碳纳米管的退沟道长度Fig. 6 Dechanneling lengths of space particles with different energies
从图6可以看到,对于硅晶体,入射粒子能量越大,退沟道长度越大,说明粒子越难以退出晶体束缚;对于碳纳米管,入射粒子能量越大,退沟道长度越小,说明粒子越容易退出晶体束缚。在所研究的空间带电粒子能量范围内,碳纳米管的退沟道长度远大于硅晶体,说明碳纳米管对空间粒子的束缚能力更强。
由图6可见,在能量相同的情况下,质子的退沟道长度大于电子的退沟道长度,这是因为在硅晶体中,退沟道长度与粒子动量和速度的乘积成正比,根据式(6),动能相同的条件下,质子动量和速度的乘积大于电子动量和速度的乘积,导致质子退沟道长度略大于电子的。这意味着晶体捕获相同能量的粒子后,质子可以在晶体的束缚下运动更长的距离。
4)偏转效率
取弯曲半径R=1 cm,根据式(5),计算0.04~7 MeV能量范围电子和0.1~400 MeV能量范围质子入射硅晶体和碳纳米管的偏转效率,如表1和图7所示。

表1 电子入射硅晶体和碳纳米管的偏转效率(R=1 cm)Table 1 Deflection efficiency of different energy electrons at different bending angles (R=1 cm)

图7 质子入射硅晶体和碳纳米管的偏转效率(R=1 cm)Fig. 7 Deflecting efficiency of different energy protons at different bending angles (R=1 cm)
从表1和图7所示的数据可以看到,硅晶体的偏转效率远低于碳纳米管,即使偏转角度仅为0.1°的情况下,硅晶体对电子的偏转效率几乎为0,没有应用价值。这是因为硅晶体的退沟道长度远小于碳纳米管的退沟道长度,造成偏转效率非常低。
2.2 硅晶体与碳纳米管比较
晶体势垒对带电粒子起到束缚作用,硅晶体的势垒约为22.7 eV,碳纳米管的势垒约为60 eV,因此碳纳米管对带电粒子的束缚作用强。从关键参数的分析效果看,碳纳米管对应带电粒子的临界角和临界半径略大于硅晶体的,但退沟道长度远大于硅晶体,这就使得碳纳米管的偏转效率也远大于硅晶体的。
从实际效果看,即使偏转角度(晶体弯曲角度)仅为0.1°,硅晶体对空间电子已经基本不具备偏转效果,可见对于空间粒子偏转,硅晶体没有工程应用价值。与硅晶体正好相反,即使偏转角达到45°,碳纳米管对空间电子和质子的偏转效率仍超过20%。
为了实现对空间带电粒子的有效偏转,需要将带电粒子偏转较大角度,因此需要将晶体进行大角度弯曲。硅晶体质地硬,大角度弯曲操作很困难;碳纳米管质地柔软,大角度弯曲操作容易。
综上,尽管目前碳纳米管的试验结果还不丰富,但碳纳米管的偏转效率、弯曲性能均优于硅晶体,更具备工程应用前景。
3 空间带电粒子偏转屏蔽应用初探
3.1 弯曲晶体单元设计
利用弯曲晶体对带电粒子进行偏转,要求入射粒子的方向与弯曲晶体轴向的夹角小于临界角,由此对粒子入射方向存在限制。空间带电粒子的方向是各向同性的,4π空间均存在入射粒子,因此需建立合理的晶体结构,使其可偏转空间各向同性入射的带电粒子。
针对空间各向入射粒子,构建了如图8所示的弯曲晶体单元,该单元由不同弯曲半径的弯曲晶体组成,弯曲半径为粒子的临界半径,弯曲角度为90°。考虑到碳纳米管具备良好的弯折性能,因此该结构采用碳纳米管材料。该结构的最大弯曲半径和厚度均为粒子最大能量对应的临界半径。带电粒子能量越大,临界半径越大,因此该单元中弯曲半径越大的弯曲晶体,可屏蔽的带电粒子的能量越大。
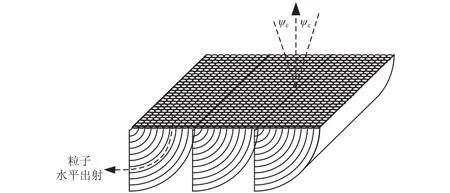
图8 弯曲晶体单元结构示意Fig. 8 Schematic diagram of bent crystal unit
入射带电粒子一旦被捕获到弯曲晶体沟道中,就可以沿着沟道运动,最终水平出射。当待屏蔽物体位于该结构下方时,因粒子水平出射,无法入射到下方物体,从而实现对下方物体的屏蔽。
图8所示的弯曲晶体单元除了可以捕获垂直入射的粒子外,对于处于弯曲晶体同一平面的斜入射粒子也具备捕获效果。从图9(a)可以看到,粒子倾斜入射到弯曲晶体中,当入射粒子的方向与弯曲半径的切线方向重合或者与切线方向的夹角小于临界角ψc,且弯曲半径大于粒子临界半径时,则满足捕获条件,粒子可以被捕获到弯曲晶体中,从而实现偏转。由此可以看到,图8构建的弯曲晶体单元可以捕获θ∈[0, π/2]空间范围、ψ∈[-ψc, +ψc]入射角范围内的带电粒子,如图9(b)所示。
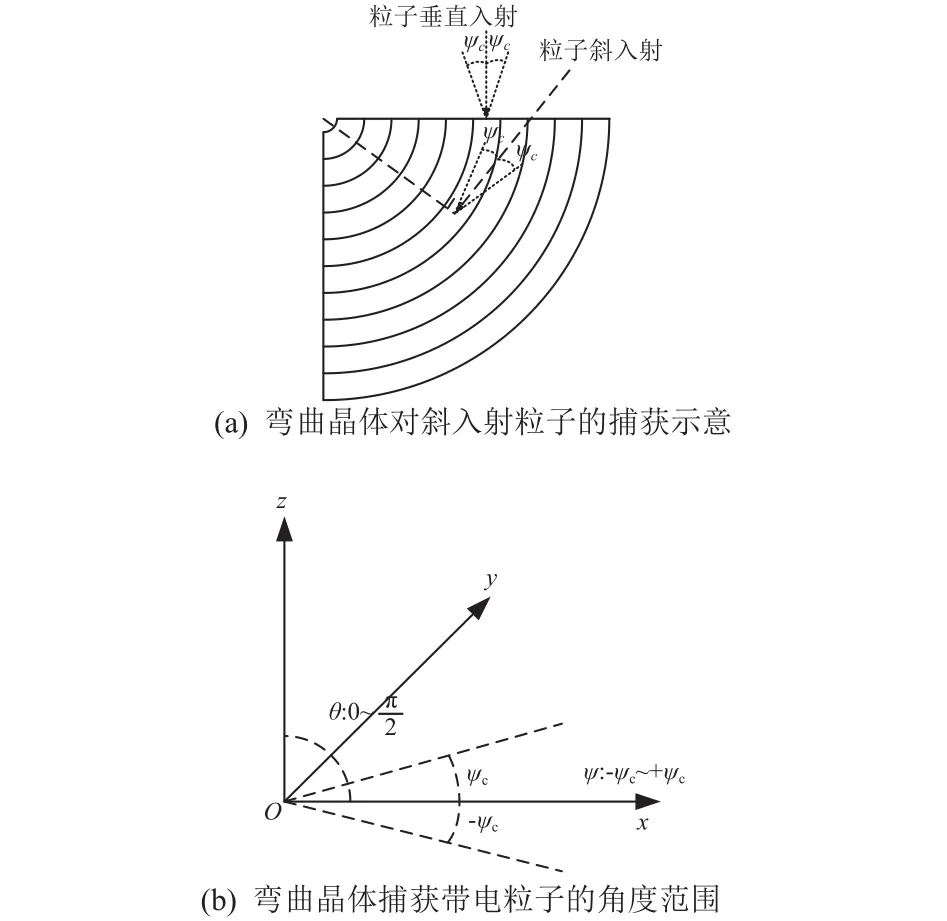
图9 弯曲晶体单元捕获同一平面不同方向入射粒子示意Fig. 9 Schematic diagram of different injecting direction particles on the same plane captured by bent crystal unit
将图8所示弯曲晶体单元从上至下组装,每一层相对于上一层旋转2ψc角度,从而构建单元阵列,如图10所示,则第n层可覆盖θ∈[0,π/2]空间范围、ψ∈[2(n−1)ψc−ψc,2(n−1)ψc+ψc]入射角范围内的带电粒子;共组装N=2π/(2ψc)层后,可覆盖θ∈[0, π/2]空间范围、ψ∈[0, 2π]入射角范围内的粒子,从而实现对2π空间入射带电粒子的捕获和偏转。为确保可针对最大能量入射粒子的捕获和偏转,ψc可选取入射粒子最大能量对应的临界角。在被屏蔽物体周围均采用同样的结构进行防护,即可实现对4π空间入射带电粒子的偏转。

图10 弯曲晶体单元捕获同一平面不同方向入射粒子示意图(碳纳米管)Fig. 10 Isotropous coplanar particles captured by bent crystal unit (carbon nanotube)
3.2 偏转屏蔽方法与传统屏蔽方法比较
采用上述屏蔽结构对空间带电粒子进行偏转屏蔽分析。2.1节中给出,空间0.04~7 MeV能量范围的电子在碳纳米管中的临界角范围为2.3°~0.3°,临界半径范围为91 nm~9 μm。按照最大能量电子对应的参数构建屏蔽结构,每层屏蔽结构的厚度为 9 μm,共需构建 360°/(2×0.3°)=600 层,则屏蔽总厚度为5.4 mm。该结构在5.4 mm的屏蔽厚度条件下,存在一定的概率将7 MeV的电子偏转到水平方向,从而实现对其下方物体的屏蔽。传统上采用能量损失原理进行带电粒子屏蔽时,7 MeV电子在碳中的射程约为17.9 mm[13],即需要17.9 mm厚度的碳层才可实现对7 MeV电子的屏蔽。仅从屏蔽厚度考虑,利用弯曲晶体的结构屏蔽空间电子时优于传统方法。
采用同样的方法可针对质子建立屏蔽结构,2.1节中同时给出,空间0.1~400 MeV能量范围的质子在碳纳米管中的临界角范围为1.4°~0.02°,临界半径范围为24 μm~0.8 mm。按照最大能量质子对应的参数构建屏蔽结构,每层屏蔽结构的厚度为0.8 mm,共需构建 360°/(2×0.02°)=9000 层,则屏蔽总厚度为7.2 m。传统上采用能量损失的原理进行带电粒子屏蔽防护时,400 MeV质子在碳中的射程约为40.7 cm[14]。可见利用弯曲晶体结构对质子进行偏转屏蔽,从屏蔽厚度角度考虑要比传统方法差得多。
3.3 小结
传统屏蔽方法是利用带电粒子与物质中电子碰撞损失能量的原理来降低带电粒子的能量,当屏蔽厚度超过带电粒子射程后,可以降低带电粒子的通量,从而达到降低辐射剂量的效果;目前航天器设计中的舱板屏蔽、机壳屏蔽、局部钽屏蔽等均基于此原理。这种方法的局限性是粒子能量越高,则粒子射程越长,所需屏蔽物质越厚,由此增加的屏蔽质量就越大。
偏转屏蔽方法利用的是物质内部的规则电势场,将带电粒子进行偏转,从而减少穿越至屏蔽层后方的带电粒子,达到降低辐射剂量的效果。该方法利用了晶体内部的微观势场,以钨晶体为例,该晶体内部的电场强度达到了0.7×1013V/m,对带电粒子的偏转能力是传统磁铁的104倍[1]。
偏转屏蔽方法除具备对带电粒子的偏转能力外,同时也具备传统屏蔽方法的作用。采用弯曲晶体对带电粒子进行偏转屏蔽时,粒子如果未被捕获到沟道中,则会在屏蔽物质内产生能量损失,这与传统屏蔽方法是一致的。因此,该结构同时具备传统方法中对带电粒子能量损失的作用,以及沟道效应的偏转效果,从此定性的角度考虑,弯曲晶体屏蔽结构对空间带电粒子的屏蔽效果要优于传统的能量损失方法。
采用图10所示的偏转晶体结构对空间带电粒子进行屏蔽时,可将一定比例的带电粒子偏转到水平方向,从而降低晶体结构下方防护对象接受到的带电粒子通量,减少防护对象的受辐射剂量。但该方式存在一定的缺陷,即由于将一定比例的带电粒子偏转到水平方向,会导致水平方向的粒子通量增强,当该方向存在其他对象时,该对象会接受到更多的辐射剂量。
4 仿真分析
Bagli在Geant4中实现了晶体对带电粒子偏转作用的仿真[15],并在Geant4中提供了相应的开源程序[16]。目前该程序只支持固体晶体的分析,不支持碳纳米管分析;且只支持晶体单一方向弯曲,不支持晶体旋转后的分析,无法开展图10所示的组装弯曲晶体分析,只能开展晶体单一方向弯曲、粒子垂直入射情况的仿真。
应用Bagli在Geant4-10.3版本中提供的开源程序开展晶体对带电粒子偏转仿真分析,弯曲晶体采用 Si(1, 1, 1),尺寸为 0.5 mm×10 mm×10 mm,其中厚度为0.5 mm,弯曲长度为10 mm。文献[3]中最大弯曲角度设置为30 mrad(即1.7°),弯曲半径设置为333 mm,弯曲方向为图11中红色箭头所示的反方向;防护对象设置为0.5 mm×0.5 mm×0.5 mm的硅晶体,距离弯曲晶体10 mm。防护对象位于弯曲晶体上方,粒子从弯曲晶体下方垂直入射,粒子源设定为400 MeV的质子。根据以上设置,偏转后的粒子与中心的距离为30 mrad×20 mm=0.6 mm,大于防护对象的尺寸(0.5 mm),因此可以确保偏转后的粒子不会击中防护对象。

图11 Si(1,1,1)晶体偏转400 MeV质子仿真示意Fig. 11 Simulation of 400 MeV proton bent by Si(1,1,1)crystal
图11给出了不加入晶体偏转效应(图11(a))和加入晶体偏转效应(图11(b))2种情况下,晶体对400 MeV质子的作用效果。在不加入晶体偏转效应的条件下,绝大多数质子击中了防护对象;在加入晶体偏转效应的条件下,质子发生了明显偏转,绝大多数粒子未击中防护对象。如图12所示,加入晶体偏转效应后,粒子角度主要分布在1.7°附近,与晶体弯曲角度一致,证实了弯曲晶体的偏转效果。
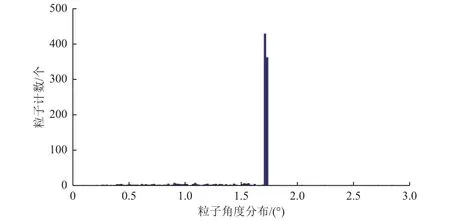
图12 400 MeV质子被Si(1,1,1)晶体偏转后的角度分布Fig. 12 Angle distribution of 400MeV proton bent by Si(1,1,1) crystal
Si(1, 1, 1)晶体偏转400 MeV质子的仿真结果见表2,可以看到,加入晶体偏转效应后,击中防护对象的粒子数降低了2个数量级,防护对象受到的辐射剂量也降低了1个数量级左右。
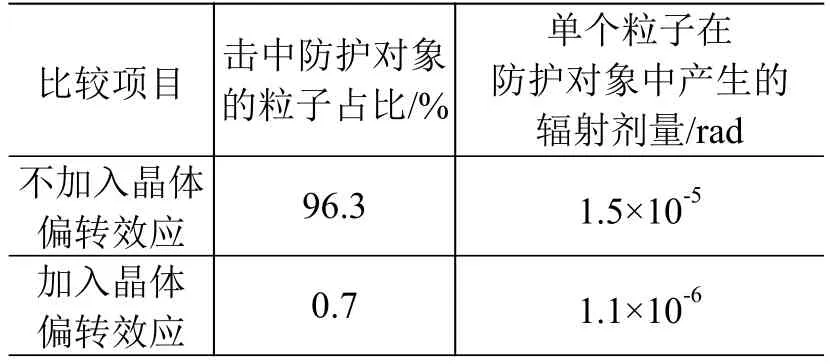
表2 Si(1,1,1)晶体偏转 400 MeV 质子仿真结果Table 2 Simulation result of 400 MeV proton bent by Si (1, 1, 1) crystal
本次仿真结果给出的偏转效率约为99.3%,高于图7给出的偏转效率约为50%的结果,这是因为本次仿真采用的晶体弯曲半径为333 mm,远大于图7计算采用的弯曲半径1 cm的数据,从式(5)可以看到,晶体弯曲半径越大,偏转效率越高。
5 结束语
本文介绍了带电粒子在晶体沟道中的偏转机理,以临界角、临界半径、退沟道长度和偏转效率4个关键参数为基础进行了偏转效果分析。并以硅晶体和碳纳米管作为载体,针对地球辐射带中0.04~7 MeV的电子和0.1~400 MeV的质子,分析了4个关键参数的影响。结果表明,对于同等能量的带电粒子,碳纳米管具有较大的临界角、较小的临界半径、较大的退沟道长度和较高的偏转效率。此外,碳纳米管更容易进行大角度弯曲操作;因此,相较于硅晶体,尽管目前碳纳米管的试验结果还不丰富,但更具备工程应用前景。
针对空间粒子各向同性入射的特点,建立了可偏转各向同性入射粒子的结构。对该结构所需屏蔽厚度的分析表明,偏转屏蔽的方式较传统屏蔽方法而言只适用于电子。从屏蔽效果看,该结构同时具备传统方法中对带电粒子能量损失的作用,以及沟道效应的偏转效果,因此屏蔽效果要优于传统的能量损失方法。但偏转屏蔽方式会增加粒子偏转方向的通量,造成该方向辐射剂量增大,故应用时应确保粒子增强方向的器件或单机可接受增强的剂量,或者粒子增强方向无电子元器件或单机,必要情况下,应针对整个航天器进行屏蔽。
采用基于Geant4的程序针对单一弯曲方向晶体、垂直入射粒子进行了初步仿真分析,结果显示在条件设置合理的情况下,弯曲晶体可降低粒子通量2个数量级和辐射剂量约1个数量级。后续将针对目前的仿真程序进行改进,使之适用于旋转晶体的分析,从而针对文中构建的适用于各向同性入射粒子的偏转晶体屏蔽结构开展分析,获取针对空间粒子的防护效果。
