基于空间分布的混凝土坝变形缺失信息估计方法
2019-04-24胡添翼
胡添翼
(上海市政工程设计研究总院水利水运设计研究院,上海 210098)
1 研究背景
为了解混凝土坝变形状态,工程人员常在坝体及其周围布设变形测点,定期获取外观变形数据,从而构建混凝土坝的变形场[1-2]。事实上,混凝土坝变形数据来自不同空间坐标的变形监测点,这些变形数据分布在一定的空间区域中,是典型的时空数据,具有时间性、空间性、复杂性、海量性、多维性、不确定性等多种特点,给相应的时空数据挖掘带来诸多挑战[3];同时,变形数据作为时空数据挖掘的数据基础,一般分布在一定尺度的时间和空间范围内,受到时空范围内各种因素的综合影响,因而实际获取的数据可能存在着各种各样的潜在问题,如数据异常、数据残缺等,数据挖掘领域称这样的数据为“受污染的数据”[4]。美国麻省理工学院的科研人员在1992年研究发现,大部分时空数据都存在不同程度的精度问题[5],时空数据污染是一种广泛存在的现象。
工程实际中,一般基于固定的时间间隔收集混凝土坝变形数据,例如每日一测或每周一测,从而建立每一个监测点的变形序列,了解其变形状态;但是由于人为失误、仪器损坏、数据丢失等不可控原因,往往会造成变形数据的缺失,从而影响变形数据的完整性。变形数据的缺失可能会造成非常严重的后果,如无法获知该测点在数据缺失期间的变形数据,所以无法获取该时段测点附近区域的变形大小,难以了解该区域的变形状况;如果变形数据长期缺失,此时一旦发生异常变形而无法被及时发现,可能造成的后果不堪设想;此外,由于数据缺失,对于变形分析模型的参数估计也会受到影响,导致分析模型的精度下降。如果能够采用一定方法对变形数据的缺失信息进行有效的估计或补偿,对了解该测点某阶段的变形情况无疑非常有帮助[6]。
本文针对上述问题,从空间的角度研究混凝土坝变形监测缺失信息的估计方法,从而尽可能还原时空数据挖掘的对象,并通过工程实例,验证本文提出的缺失信息估计方法的有效性。
2 变形缺失信息的传统处理方法
造成变形时空数据不完整的原因有很多,一方面可能是由于数据本身的问题,如数据本身存在缺失值,序列不完整;另一方面可能是在其他数据处理过程中造成的数据缺失,如剔除异常或含有粗差的监测值之后造成变形数据不完整。
针对不完整的时空数据,目前主要有以下2种处理方法:
(1)忽略法。一般情况下,因为无法完全还原真实的变形数据,针对缺失值的不合理估计可能反而会在分析模型中造成偏误,所以忽略掉缺失的数据,不作处理。
(2)似然值法。在一些特定的情况下,如需要研究某一时刻变形数据的空间分布情况,或者采用的变形分析模型对原始数据有等距性要求(如很多针对时间序列的分析方法都要求数据是等距的),仍然需要对缺失的数据进行估计,用当时最可能的似然值代替缺失值。
3 基于空间分布的缺失信息估计方法
混凝土坝作为一种典型的大型空间结构,其结构在不同尺度上都具有一定的整体性,如混凝土重力坝的单个坝段以及混凝土拱坝的整个坝体等;同时,因为其结构的整体性,其变形值的分布在空间上也具有一定的连续性。基于这种空间连续性假设,本文提出对某些缺失的变形值进行估计的方法。
3.1 空间邻近点回归插值法
假设某混凝土坝坝体结构完整,不存在明显的结构缺陷,有3个在空间上邻近且结构上相关的监测点A,B,C,如图1所示,虚线表示变形后的坝体。
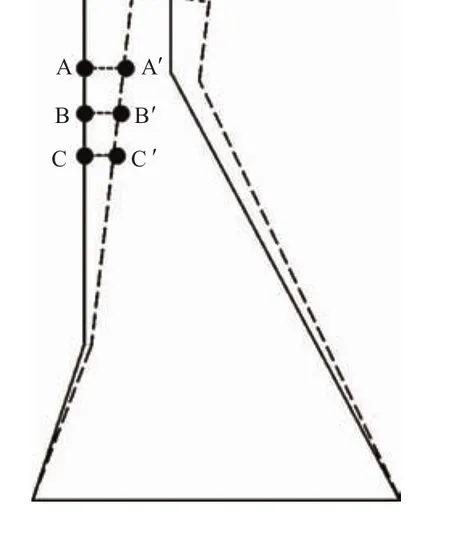
图1 混凝土坝测点变形示意图Fig.1 Demonstration of deformation at monitoring points of concrete dam
其中,测点A和C的数据是完整的,但是测点B有一段数据是缺失的,具体如图2所示。
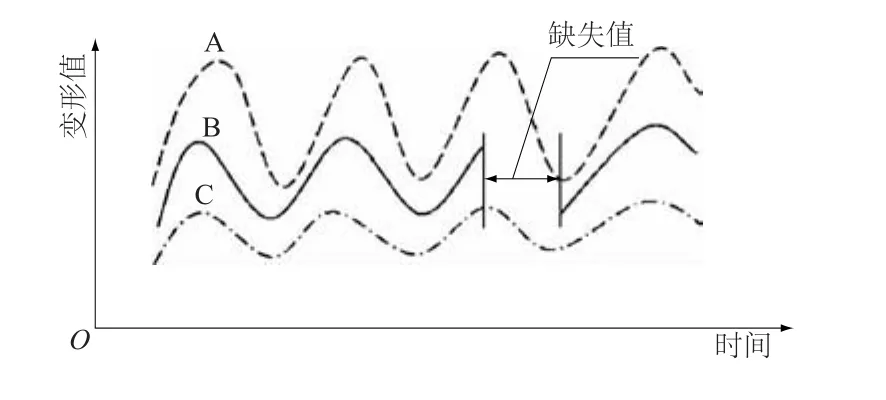
图2 部分数据缺失示意图Fig.2 Partial data missing
如果同时考虑测点A,B,C的空间邻近性,那么测点B的缺失值应该与测点A和测点C在缺失时段的变形值有关,因此可以以测点A和测点C所提供的变形信息作为依据,将测点B的变形序列δB表示为测点A和测点C变形值的函数,则有如下表达式。
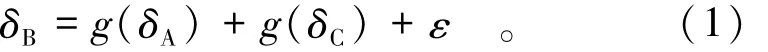
式中:g(δA)和g(δC)分别表示测点A和测点C的变形值关于δB的函数;ε表示残差。但因为大坝结构的复杂性,并不能直接判断变形值之间是线性相关还是非线性相关,这里采用多项式的形式对δA和δB、δB和δC之间的关系进行表达,借助散点图对模型的次数进行估计,则有
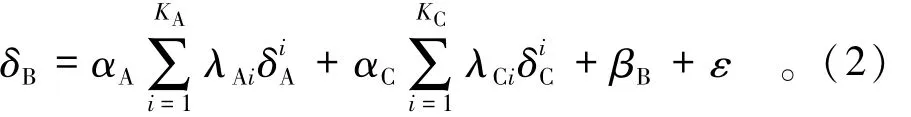
式中:αA和αC分别为含有δA和δC的多项式的系数;KA和KC为多项式的最高次数,该值可以通过绘制δB与δA,δB与δC的相关关系散点图进行确定;λ为回归系数;βB为平移项。
进一步,如果考虑更加普遍的情况,针对任一有缺失数据的监测点i的变形序列δit,则有
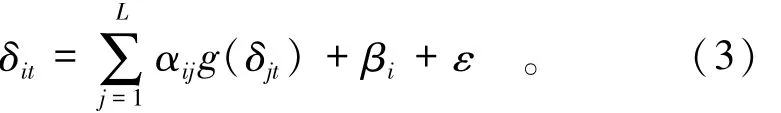
式中:δjt表示与δit相邻测点的变形序列;L表示和测点i相邻近的测点的数量(可以设置一定的临界距离,判断点与点之间的邻近关系);g(δjt)表示δit和δjt之间的关联函数(这里采用多项式进行表达);αij表示回归系数;βi表示测点i的平移项。
根据δit和邻近测点已有的变形数据用最小二乘法可对αij的数值进行估计,从而最终确定模型的表达式。为了衡量模型的有效性,可计算模型的决定系数;决定系数越大,自变量对因变量的解释程度越高。
3.2 空间反距离加权插值法
如果采用最小二乘法估计的效果不佳或者缺失的数据较多,可以采用反距离加权空间插值方法[7-9]对变形数值进行估计,即认为缺失测点的数据是邻近测点加权平均的结果,此时邻近测点变形值的权重之和为1,即有:
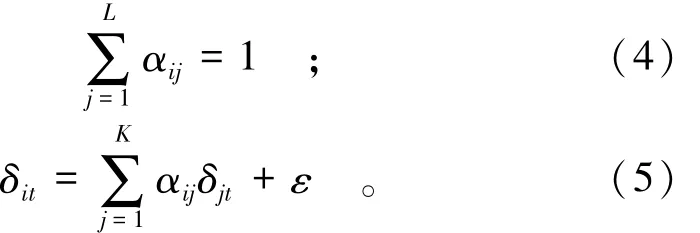
式中αij的取值和测点i和周围测点的空间距离有关。根据“地理学第一定律”[10-11],空间距离越近的两个点,其相关性越强,因此可以取:
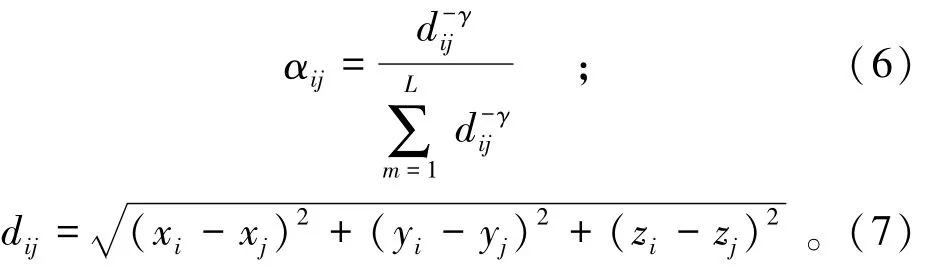
式中:dij表示测点i和测点j之间的空间距离;系数γ一般取1或2。
相较于式(3),式(5)虽然有一定的近似,但其优点在于变形的估计值仅仅和估计点的空间位置有关,因此可以估计一定空间范围内任意一个点的变形值大小;同时,因为对系数的估计不需要借助于最小二乘回归,其对缺失数据的数量没有要求。
4 工程实例
为验证本文提出的变形缺失信息估计方法的有效性,以某混凝土重力坝的变形数据为例进行实例分析。
4.1 工程概况
某混凝土重力坝最大坝高为185 m,坝体根据功能被分为左非、航运、左厂、泄水和右非等多个坝段。其中,泄水坝段为重点监测坝段,有4个重点监测断面,这里简记为1—4号断面。为监测坝体水平位移,4个断面均布置有正、倒垂线组。
以断面1为例,上面7个测点的变形过程线如图3所示。可以发现,这些测点的变形过程线具有比较强的相关性。

图3 断面1测点变形过程线Fig.3 Process lines of deformation at monitoring points in section 1
4.2 变形缺失信息估计
下面讨论变形缺失数据的估计问题,以图3中的测点PL5-4为例,人为构造长达2个月(2014年7—8月)的缺失段,为便于估算,也列出其他2个测点的数据过程线,具体如图4所示。

图4 测点PL5-4数据缺失过程线Fig.4 Process lines of missing data at monitoring point PL5-4
将PL5-4和另外2个测点的相关关系用相关图的形式表达出来,具体如图5所示。
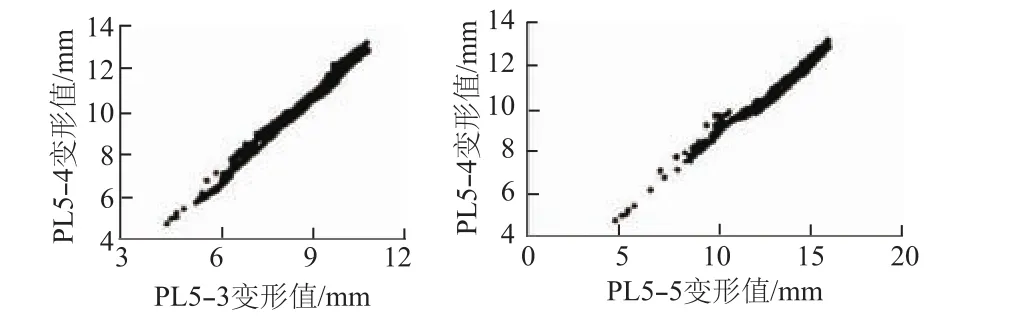
图5 3个测点的相关关系分布Fig.5 Correlation of deformation between monitoring points
根据图5的结果可以看出,测点PL5-4和邻近测点呈现很明显的线性相关。分别采用式(3)、式(5)以及传统的线性插值对缺失段进行估计。其中,根据式(3)得到的估计公式为

根据式(5)得到的估计公式为
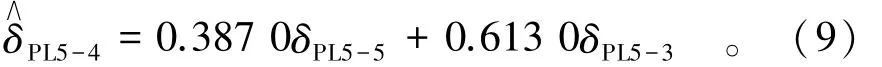
根据式(8)和式(9)可以得到缺失值的估计序列,将原序列以及传统的线性插值序列共同绘制于图6。这几种估计方法的估计精度如表1所示。
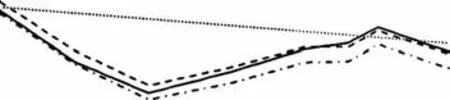
图6 测点PL5-4数据缺失值估计过程线Fig.6 Process lines of estimated missing values for monitoring point PL5-4

表1 测点PL5-4数据缺失值估计精度Table 1 Accuracy of estimated missing values for monitoring point PL5-4
根据图6和表1可以发现,本文提出的缺失值估计方法具有较高的估计精度,其中空间邻近点插值方法的估计效果最佳,决定系数和均方根误差都是最优的;空间反距离加权插值法的估计效果次之,但是它的优势在于可以估计一定空间内任意测点的变形值;线性插值的效果最差,尤其是本例这种长时间段数据缺失的情况下,其估计结果的误差远远大于前面2种方法。
5 结 语
为解决混凝土坝变形数据缺失的问题,本文基于空间分布提出了相应的缺失信息估计方法,具体为空间邻近点插值法和空间反距离加权插值法。工程实例表明,本文提出的这2种方法计算简单明了,且都具有一定的有效性和精确性,可以较好地估计变形序列中的缺失信息;其中空间邻近点插值方法的估计精度最高,而空间反距离加权插值法的优势在于可以估计一定空间内任意测点的变形值。
但是,该方法目前仍有以下几点值得改进:①该方法主要针对空间中某一个测点数据缺失,而周围测点数据完整的情况,如果大范围测点出现数据缺失,本文方法的适用性会受到影响;②由于假设条件多,空间反距离插值法对于边缘测点的估计精度不高,需要进一步改进;③在本文中,空间测点变形值之间的函数关系是通过散点图进行确定的,如果能够从力学角度对其进行进一步分析,模型的精度会进一步提高。
