应用GA-BP神经网络预估砾类土的最大干密度

饶云康，丁 瑜，2，3，许文年，2，3，张 亮，张 恒，潘 波

（1.三峡大学三峡库区地质灾害教育部重点实验室，湖北宜昌 443002；2.三峡大学防灾减灾湖北省重点实验室，湖北宜昌 443002；3.三峡地区地质灾害与生态环境湖北省协同创新中心，湖北宜昌 443002）

1 研究背景

根据规范［1］，粗粒土分类中，砾粒组（粒径在2～60 mm之间）含量大于砂粒组（粒径在0.075～2 mm之间）含量的土称为砾类土。砾类土广泛用于各类工程填筑，其变形、强度、渗透等特性与压实程度密切相关。实际工程中，砾类土的最大干密度是评价填料压实性能、控制填筑工程质量的重要参数［2］。

砾类土最大干密度与颗粒级配、土粒相对密度等有关。砾类土土粒的相对密度虽略有差异，但变化幅度很小。土粒相对密度不是影响最大干密度的主要因素。土体因颗粒级配不同，将形成不同的机械填充，因而颗粒级配决定了土体的最大压实程度。因此，颗粒级配通常被认为是控制砾类土最大干密度的关键因素［3-4］。

对于级配特征与最大干密度之间的关系，一些学者进行了有益探讨。冯瑞玲等［3］通过分析8组粗粒土试验数据，建立了最大干密度与5个特征粒径（d10，d30，d50，d60，d90）之间的回归方程（dm为累计质量含量为m%对应的颗粒直径）；朱俊高等［5］提出了由不均匀系数Cu、曲率系数Cc和最大粒径d100组成的级配参数λ，通过分析拟合19组砾类土试验数据，建立了最大干密度与级配参数λ之间的4次多项式关系；左永振等［6］在朱俊高等［5］研究的基础上提出了由Cu、Cc、＜5 mm粒组含量和d100组成的级配参数λ′，通过分析拟合15组砾类土试验数据，建立了最大干密度与级配参数λ′之间的3次多项式关系。分析不难发现，这类经验分析方法试图通过某些关键粒径或指标描述级配特征，建立最大干密度与指标之间的相关关系。由于选取的指标不同，加之指标数量有限，得到的经验关系式通常存在明显的适用局限性。

砾类土的颗粒级配分布范围广泛，粒组含量变化不定，差异大，人工神经网络为预估最大干密度的影响提供了有效途径［2，7］。文献［2］以 26组不同级配的非均质土石混合料试验数据作为学习样本，建立了最大干密度的预测模型，但对粒组相对含量仅划分为＜5，5～40，＞40 mm，显然难以充分表征颗粒级配。文献［7］采用24组不同级配的粗粒土试验数据作为学习样本，以Cu、Cc、分形指标和7个粒组（即＜0.075，0.075～2，2～5，5～10，10～20，20～40，40～60 mm）表征颗粒级配建立预测模型，表征颗粒级配的参数较多，但选取样本的最大粒径均为60 mm，未考虑不同d100的影响。

建立合理的神经网络预测模型，准确描述颗粒级配，选取足够的具有代表性的样本至关重要。神经网络对于输入层与隐含层、隐含层与输出层神经元之间初始的连接权值，隐含层和输出层初始的阈值非常敏感，若这些参数设置不合理，会导致模型收敛速度很慢和陷入局部最优［8］。为此，本文通过参考相关文献选取92组砾类土试验数据，考虑全级配（d10，d20，…，d100），利用遗传算法优化 BP神经网络的初始权值与阀值，构建基于BP神经网络和遗传算法的砾类土最大干密度预估模型。

2 样本选取与数据处理

2.1 样本选取

通过查阅，分别从文献［3］、文献［5］、文献［6］、文献［7］、文献［9］、文献［10］、文献［11］、文献［12］、文献［13］整理得到 5，19，15，26，6，8，4，5，4组砾类土最大干密度样本数据，共92组。所选样本均属于规范［1］的砾类土定义范围，且属于无黏性自由排水粗粒土［14］（＜0.075 mm粒径的质量百分含量≤15%）。此外，文献［3］中d10为19.8 mm的样本虽符合定义要求，但相比于其他样本d10太大，故本文并未选用。样本级配均为未经过剔除法、相似级配法等方法进行缩尺的原始级配，样本最大干密度均由规范［14］规定的表面振动压实仪法或振动台法测得，且均采用干土法，避免了不同含水率的影响。

选取的样本最大干密度为1.765～2.400 g／cm3，为典型的砾类土最大干密度范围。样本最大粒径为100～10 mm，既有大粒径也有小粒径的砾类土。样本的最大干密度、颗粒粒径涵盖范围广，具有代表性。

2.2 数据处理

对于92组砾类土数据，采取如下数据处理方式：首先，根据样本数据利用Excel绘制粒径累计曲线；然后，由粒径累计曲线获取全级配d10～d100粒径。为避免手工操作误差，利用图表数字化工具（GetData Graph Digitizer）从粒径累计曲线中准确获取粒径。

3 GA-BP神经网络预估模型

3.1 GA-BP神经网络构建

本文采用常用的3层网络结构，采用试凑法确定隐含层神经元个数。首先，由经验公式［15］J＝a（J为隐含层神经元个数，m为输入层神经元个数，n为输出层神经元个数，a为0～10之间的常数）确定隐含层神经元个数的范围。根据经验公式求得该神经网络隐含层神经元个数范围为4～14。然后分别在4～14个隐含层神经元条件下用相同的参数设置和训练样本重复建模20次，每次都用相同的检测样本进行测试，通过对比20次检测样本的平均相对误差，最终确定隐含层最优神经元个数为11个。

BP神经网络传统的梯度下降法具有收敛速度慢、易陷入局部最小值等不足，而L-M（Levenberg-Marquardt）算法可改善传统算法的不足，提高网络的收敛速度，以及增加网络训练的精度［16］。为此，本文网络训练函数采用trainlm函数，trainlm函数使用L-M算法，学习速率基值为0.001、学习速率减少率为0.1、学习速率增加率为10、最大学习速率为1×1010。

GA-BP神经网络模型通过MatLab软件编程实现，遗传算法采用gaot工具箱，基本步骤如下：

（1）数据归一化，划分样本。导入92组样本数据，将样本数据归一化到［-1，1］，选取非文献［9］的86组样本作为训练样本，文献［9］的6组样本作为检测样本。

（2）创建BP神经网络。网络采用3层结构，输入层有 10个神经元，分别代表 d10，d20，...，d100；输出层有1个神经元，代表最大干密度；隐含层有11个神经元；隐含层传递函数为tansig函数，输出层传递函数为purelin函数，网络性能函数采用均方误差mse函数；最大迭代次数为300次，目标误差值为3×10-3，最低性能梯度为 1×1010。

（3）产生初始种群。编码方式采用浮点数编码，个体由输入层与隐含层、隐含层与输出层神经元之间的连接权值、隐含层和输出层的阈值4部分组成，BP神经网络为10-11-1结构，因此个体编码长度为10×11+11×1+11+1＝133。个体中的变量范围为［-3，3］，种群规模为 100。

（4）解码，计算适应度。解码个体得到BP神经网络的初始权值和阈值，采用训练样本的网络计算值与试验值的均方误差作为目标函数值，将目标函数值的倒数作为适应度，适应度越高，均方误差越小，则该个体越优良。

（5）选择、交叉、变异，产生新种群。选择操作采用轮盘赌法选择算子；交叉操作采用算术交叉算子，即2个个体经过线性组合产生2个新的个体；变异操作采用非均匀变异算子。

（6）重复步骤（4）和步骤（5），直至达到最大遗传代数100。种群适应度进化曲线如图1所示，进化61代后种群的最大适应度保持不变，此时得到最优个体。进化82代后平均适应度与最大适应度基本重合。

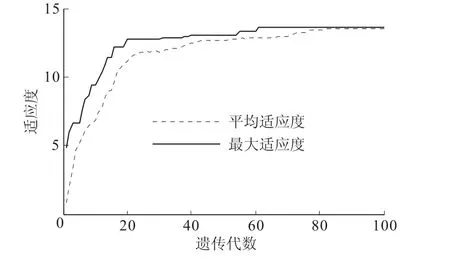
图1 适应度进化曲线Fig．1 Curves of fitness evolution

（7）解码最优个体得到优化后的初始权值和阈值。

（8）采用优化后的初始权值和阈值，利用训练样本训练神经网络。

（9）用检测样本来检验网络模型的泛化性能。

3.2 模型评价指标

采用平均相对误差MRE和决定系数R2对神经网络模型进行拟合精度评价，即：

4 结果分析与讨论

4.1 模型收敛速度

为了对比，分别采用BP神经网络和GA-BP神经网络2种方法建立砾类土最大干密度预估模型。图2为2种方法的训练窗口。BP神经网络经过59次迭代之后达到目标误差值3×10-3的要求，而采用相同的参数设置，GA-BP神经网络只需19次迭代就能达到目标误差值。表明遗传算法能优化得到合理的BP神经网络初始权值和阈值，能明显提高BP神经网络的收敛速度。

图2 网络训练窗口Fig．2 Windows of neural network training

4.2 训练样本验证

用建立的GA-BP神经网络模型预估训练样本，结果如图3所示，平均相对误差MRE为0.54%，决定系数R2为0.983，最大干密度预估值与试验值较接近，相对误差在可接受范围，精度较高。BP神经网络模型对训练样本的预估误差与GA-BP神经网络相差不大。

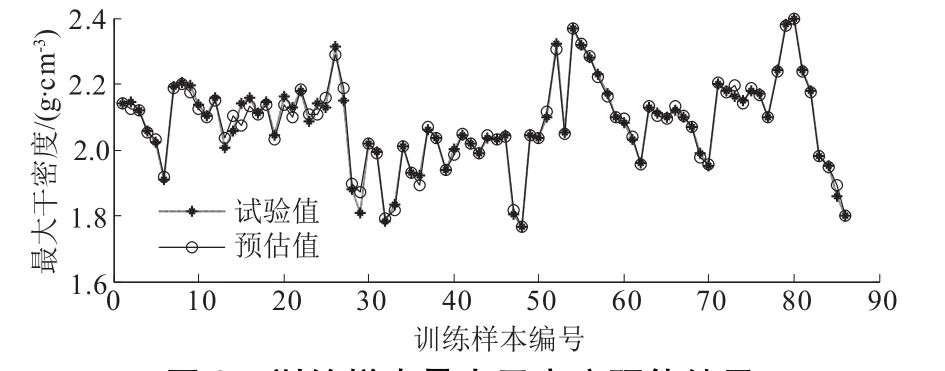
图3 训练样本最大干密度预估结果Fig．3 Estimated results of maximum dry density of training samples

4.3 预估精度及泛化性能

分别用建立的GA-BP神经网络模型、BP神经网络模型对6组检测样本进行预估，预估结果如表1所示。选取文献［9］的6组样本作为检测样本，而选取除文献［9］外的86组样本作为训练样本，保证了检测样本和训练样本来源于不同文献。

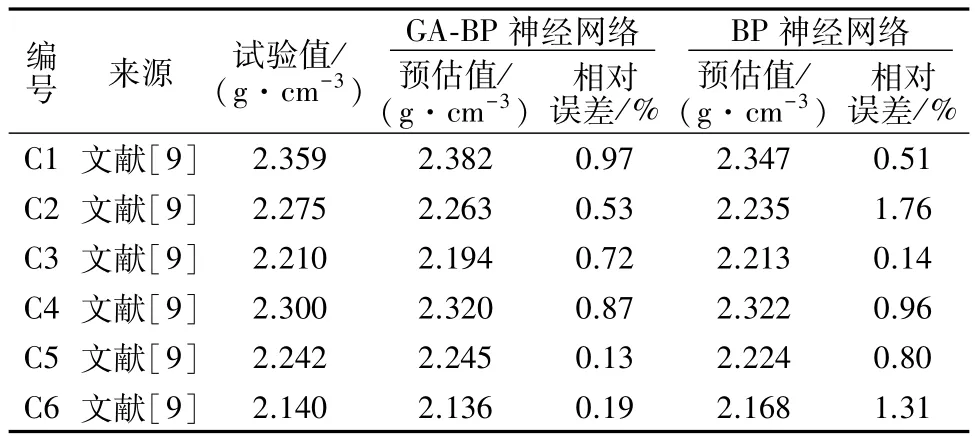
表1 检测样本的预估结果Table 1 Estimated results of test samples

对比GA-BP神经网络与BP神经网络可知，采用GA-BP神经网络的最大相对误差为0.97%，平均相对误差MRE为0.57%，最大干密度预估值与试验值较接近，相对误差在可接受范围，表明该神经网络的泛化性能良好。而采用BP神经网络，最大相对误差为1.76%，平均相对误差MRE为0.91%，预估误差明显高于GA-BP神经网络，表明GA-BP神经网络模型的泛化性能优于BP神经网络。

综上所述，考虑全级配建立GA-BP神经网络模型，最大干密度预估值与试验值较吻合，具有较好的泛化性能，且预估误差离散程度较低。颗粒级配是砾类土最大干密度的主要影响因素，该神经网络能充分反映颗粒级配对砾类土最大干密度的影响。本文研究表明，采用GA-BP神经网络，由全级配能较好地预估砾类土最大干密度，可为实际工程中砾类土选配与改善提供参考依据。

5 结 论

考虑全级配（d10～d100），采用 GA-BP神经网络构建砾类土最大干密度预估模型，并将其与BP神经网络进行对比，主要结论如下：

（1）与标准的BP神经网络相比，遗传算法能优化得到合理的BP神经网络初始权值和阈值，能明显提高BP神经网络的收敛速度，所建模型预估精度较高且泛化性能较好。

（2）86组训练样本预估结果的平均相对误差为0.54%，决定系数为0.983，6组检测样本预估结果的平均相对误差为0.57%，表明GA-BP神经网络模型能充分反映颗粒级配对砾类土最大干密度的影响，采用GA-BP神经网络，由全级配能较好地预估砾类土的最大干密度。

（3）收集各工程最大干密度数据，建立神经网络大数据平台，可为控制砾类土工程填筑压实质量、选取满足工程压实性能要求的砾类土提供最大干密度预估参考。