SPECK算法的不可能差分分析*

李明明，何 骏，郭建胜

(1.信息工程大学，河南 郑州 450001；2.郑州信大捷安移动信息安全关键技术国家地方联合工程实验室，河南 郑州 450004)

0 引言

2013年美国提出SPECK和SIMON两类超轻量分组密码算法[1]。其中SPECK算法整体采用变形Feistel结构，有着突出的软件实现性能。SPECK算法轮函数采用ARX模块，由循环移位、异或、模整数加法运算，其中模整数加法是主要非线性运算。SPECK算法自从提出以来，就受到密码学界的广泛关注，对于SPECK系列算法目前有多个安全性分析结果[2-10]。

不可能差分分析由KNUDSEN L[11]和BIHAM F[12]两人分别独立提出，是目前最常用的密码分析方法之一。对一个密码算法进行不可能差分的首要任务在于寻找概率为0的差分路径，即不可能差分区分器。其次，基于得到的不可能差分区分器，筛去错误密钥，进而确定正确密钥。

LEE H等人[13]利用MILP搜索技术，对输入差分和输出差分仅含一个非零比特的情况进行搜索，找到了SPECK64算法的一些6轮不可能差分区分器。徐洪[14]等人通过分析模加法运算的差分扩散性质，找到了SPECK32/64和SPECK48/96算法的一些6轮不可能差分区分器，并给出SPECK32/64和SPECK48/96算法的10轮不可能差分分析。李明明等人[15]利用徐洪等人给出的模整数加法差分扩散性质，分析SPECK系列算法的加密方向与解密方向的差分扩散规律，从而证明了在该性质下SPECK系列算法的不可能差分区分器至多6轮，并给出了所有6轮不可能差分区分器；此外，Li Mingming等[16]进一步给出模整数加法差分扩散的补充性质，构造了SPECK32/64和SPECK48/96算法7轮不可能差分区分器，并给出了它们的11轮不可能差分分析。但到目前为止，还没有SPECK2n(2n=64,96,128)算法的不可能差分分析结果。如果能够给出SPECK2n(2n=64,96,128)算法的不可能差分分析，则对于完善该算法的安全性分析理论具有重要的意义。

本文分析了SPECK2n(2n=64,96,128)算法在不可能差分分析下的安全性。首先通过分析模加法差分的扩散性质，找到了SPECK2n(2n=64,96,128)算法的7轮不可能差分区分器。其次，基于找到的7轮不可能差分区分器，给出了SPECK64/128算法和SPECK128/256算法的11轮不可能差分分析，以及SPECK 96/144算法的10轮不可能差分分析，恢复了全部主密钥。

1 SPECK算法介绍

本节主要对文章里出现的符号进行说明及介绍SPECK算法的基本知识。首先给出符号说明如下。

xi：第i轮输入的左半分组;

yi：第i轮输入的右半分组;

Δxi[j]：Δxi的第j比特;

>>>α：循环右移α比特;

<<<β：循环左移β比特;

Ki：第i轮子密钥;

+：模2n加;

*：不确定的比特差分。

SPECK算法是美国于2013年提出的轻量级分组密码算法，采用变形Feistel结构。该算法轮函数由循环移位、异或、模2n整数加法运算组成，即ARX模块。其轮函数如图1所示。

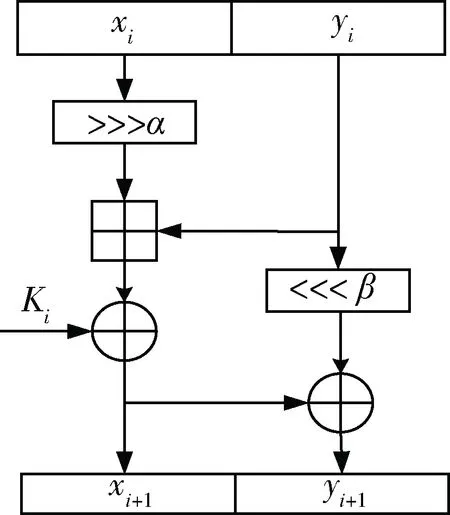
图1 SPECK系列算法轮函数

用SPECK 2n/mn来表示分组长度为2nbit，密钥长度为mnbit的SPECK算法，其中n∈{16,24,32,48,64}，m∈{2,3,4}。其密钥扩展算法如下。

密钥扩展算法记算法主密钥K=(Lm-2,Lm-3,…,L0,K0)，其中K0,Li∈{0,1}n，m为各算法密钥块的数量，m∈{2,3,4}，如SPECK128/128算法中m=2，SPECK128/192算法中m=3，SPECK128/256算法中m=4。扩展算法为：

输出N个子密钥K0,K1,…,Kn-1。若已知任意个相邻的轮密钥Ki,…,Ki-m+1，便可恢复主密钥。SPECK算法各版本及相关参数值如表1所示。

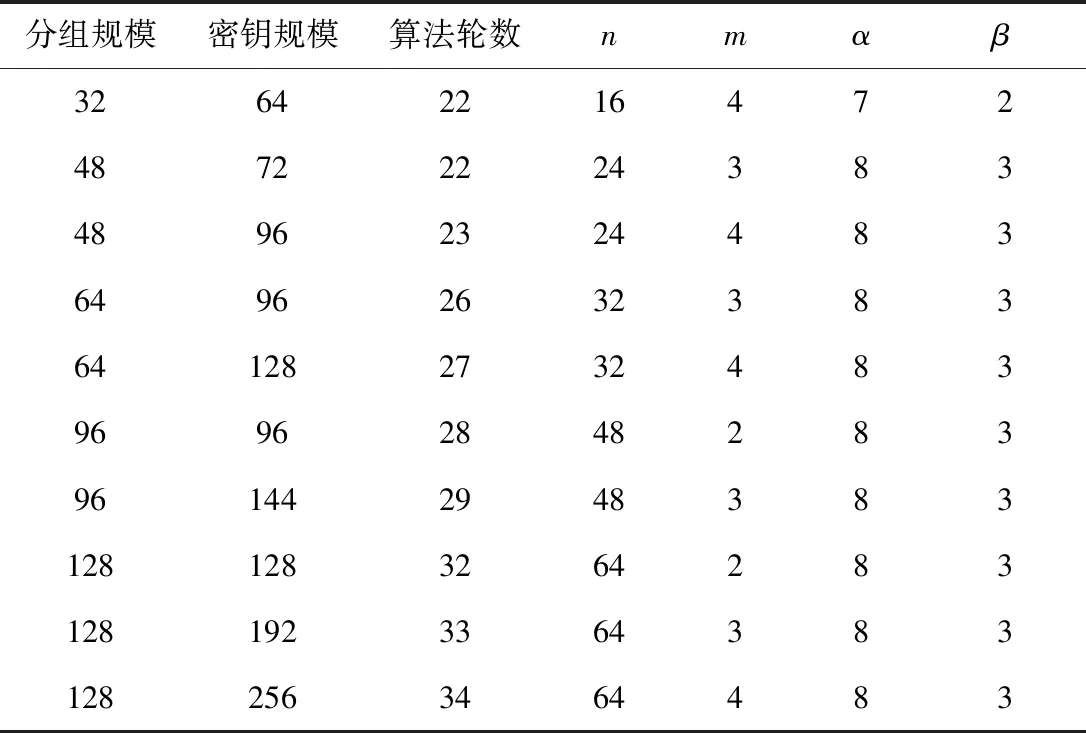
表1 SPECK系列算法版本

2 SPECK2n(2n=64,96,128)算法的7轮不可能差分区分器

首先，介绍徐洪等人给出的模整数加法的差分扩散性质，如性质1所示。

性质1[14]z=x+y(mod2n)为n比特数的模加法运算，令Δx=x⊕x′=(Δx[n-1],Δx[n-2],…,Δx[0])，Δy=y⊕y′=(Δy[n-1],Δy[n-2],…,Δy[0])分别为输入x,y的异或差分，Δz=z⊕z′=(x+y)mod2n⊕(x′+y′)mod2n=(Δz[n-1],Δz[n-2],…,Δz[0])为输出z的差分，设l1=min{k|Δx[k]=1}，l2=min{k|Δy[k]=1}，l=min{l1,l2}，则：

(1)若l1=l2=l，则Δz[l]=Δz[l-1]=…=Δz[0]=0，而当l+1≤i≤n-1时，Δz[i]=*。

(2)若l1≠l2，则Δz[l]=1,Δz[l-1]=…=Δz[0]=0，而当l+1≤i≤n-1时，Δz[i]=*。

李明明等利用徐洪等人给出的模整数加法的差分扩散性质，通过分析SPECK2n(2n=64,96,128)算法的加密方向与解密方向的差分扩散规律，证明了在该性质下SPECK系列算法的不可能差分区分器至多6轮，给出了许多SPECK2n(2n=64,96,128)的6轮不可能差分区分器，如式(1)～式(4)所示。

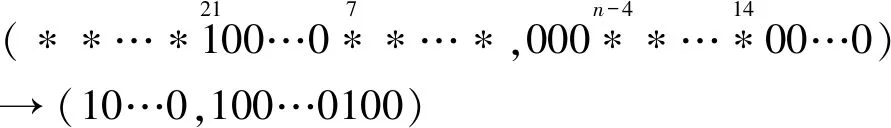
(1)

(2)

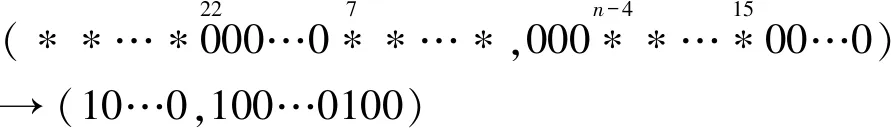
(3)

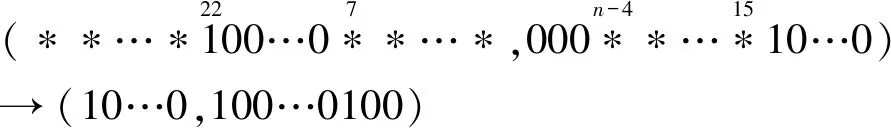
(4)

但徐洪等人给出的模整数加法差分扩散性质是一个必要不充分命题，Li Mingming等[16]进一步给出模整数加法差分扩散的补充性质，如性质2所示。

证明设x=(x[n-1],x[n-2],…,x[0])，y=(y[n-1],y[n-2],…,y[0])，输出z=(z[n-1],z[n-2],…,z[0])，进位c=(c[n-1],c[n-2],…,c[0])，则有

z[i]=x[i]⊕y[i]⊕c[i-1]，c[i]=x[i]y[i]⊕x[i]c[i-1]⊕y[i]c[i-1]，1≤i≤n-1

其中z[0]=x[0]⊕y[0],c[0]=x[0]y[0]。所以第i比特的输出差分值Δz[i]=Δx[i]⊕Δy[i]⊕Δc[i-1]。

证毕。

利用性质1和性质2，可构造SPECK2n(2n=64,96,128)算法的7轮不可能差分区分器。如定理1所示。

定理1当初始输入状态差分满足(Δx1,Δy1)=(0000000000000010,0000010000000000)且x1[1]≠y1[10]时，经7轮SPECK32算法加密后输出状态差分满足(Δx8,Δy8)=(10000000 00000000,1000000000000010)是不可能的。

证明因为x1[1]≠y1[10]，令r1=x1>>>7，则r1[10]≠y1[10]。又因为x2=((x1>>>7)+y1)⊕K1，则x2=(r1+y1)⊕K1，由性质2可知初始输入状态(x1,y1)经1轮SPECK32/64算法加密后输出差分Δx2=(0000000000000000)，故Δy2=Δx2⊕(Δy1<<<2)=(0001000000000000)；再由性质1可知，(x2,y2)再经过2轮SPECK32算法加密后输出状态差分满足Δz4[5]=1。

而差分满足(Δx8,Δy8)=(1000000000000000,1000000000000010)的状态(x8,y8)经4轮SPECK32算法解密后输出状态Δz4[5]=0。故矛盾。

证毕。

以SPECK64算法为例，选取其中一条7轮不可能差分区分器给出具体形式，如图2所示。

3 SPECK2n算法的11轮不可能差分分析

本节首先详细给出SPECK64/128算法的11轮不可能差分攻击过程；其次，利用相同的方法简要给出SPECK96/144算法的10轮不可能差分分析结果以及SPECK128/256算法的11轮不可能差分分析结果。

3.1 SPECK64/128算法的11轮不可能差分分析

利用图2给出的SPECK64算法7轮不可能差分区分器，向上扩展1轮，向下扩展3轮可得其11轮不可能差分路径，如图3所示。并结合密钥分割攻击及时空折中技术给出SPECK64/128算法的11轮不可能差分攻击如下。

(1)选择2n个明文结构，其中的明文满足x0[8,9],y0取定值，其余比特取任意值，故一个明文结构包含230个明文，可以构造259个明文对。因此攻击的选择明文量为2n+30，其中包含2n+59个明文对。

图2 SPECK64算法的7轮不可能差分区分器

(3)猜测第11轮子密钥K10。对于剩余的明文对，筛选出差分(Δx10,Δy10)满足Δt9[3,4,5]=(000)的数据对，其中Δt9=Δx10⊕Δy10，y10=(x11⊕y11)>>>3，x10=((x11⊕K10)+y10)<<<8，经这一步过滤大约

图3 SPECK64算法的11轮不可能差分路径

定理2若并行利用15条7轮不可能差分区分器对10轮SPECK64/128算法进行不可能差分分析，恢复128比特主密钥，其时间复杂度为2127.65次10轮SPECK64算法加密，数据复杂度为264个选择明文，存储复杂度为2116个SPECK64状态。

证明上述攻击过程中，时间复杂度主要由第6步决定。经第6步排除错误密钥后大约剩余ε=296×(1-2-29)2n-7个候选密钥，再对候选密钥和剩余32比特密钥进行穷举恢复密钥的时间复杂度为ε×232。当n=34时，11轮SPECK64算法不可能差分分析总时间复杂度为2n+90/11+ε×232=2n+90/11+296×(1-2-29)2n-7×232≈2127.65次11轮SPECK64算法加密，数据复杂度为250.89个选择明文。此外，存储复杂度主要由第4步决定，大约为232×227×2n+22×2≈2116个SPECK64状态。

若同时使用定理1给出的全部15条SPECK64算法的7轮不可能差分区分器，总时间复杂度可进一步降低。使用264个选择明文，此时错误率降为(1-2-29)227×15，总的时间复杂度约为15×2124/11+2128×(1-2-29)227×15≈2124.80次11轮SPECK 64算法加密，存储复杂度约为2116×15=2119.91个SPECK64状态。

证毕。

3.2 SPECK96/144算法的10轮不可能差分分析

利用定理1给出的SPECK2n(2n=64,96,128)算法的7轮不可能差分区分器，任选其中一条作为SPECK96的不可能差分区分器。在该区分器基础上向上扩展1轮，向下扩展2轮得到10轮不可能差分路径，并结合密钥分割攻击及时空折中技术可以给出SPECK96/192算法的10轮不可能差分攻击，攻击过程中需要猜测96比特密钥，选择明文数量为296，时间复杂度约为2143.66次10轮加密，存储复杂度约为2133个SPECK96状态。

若同时使用定理1中给出的其中15条SPECK96算法7轮不可能差分区分器，总时间复杂度可进一步降低。使用296个选择明文，此时错误率降为(1-2-45)243×15，总的时间复杂度约为15×2140/11+2144×(1-2-45)243×15≈2140.91次10轮SPECK96算法加密，存储复杂度约为2133×15=2136.91个SPECK96状态。

3.3 SPECK128/256算法的11轮不可能差分分析

利用定理1给出的SPECK2n(2n=64,96,128)算法的7轮区分器，任选其中一条作为SPECK128算法的不可能差分区分器。在该区分器基础上向上扩展1轮，向下扩展3轮得到11轮不可能差分路径，并结合密钥分割攻击及时空折中技术可以给出SPECK128/256算法的11轮不可能差分攻击，攻击过程中需要猜测192比特密钥，选择明文数量为2128，时间复杂度约为2192×259×2/11+2192×(1-2-61)259×264≈2192×259×2/11+2192×e-2-2×264≈2255.65次11轮加密，存储复杂度约为2244个SPECK128状态。

若同时使用16条SPECK128算法7轮不可能差分区分器，总时间复杂度可进一步降低。使用2128个选择明文，此时错误率降为(1-2-61)259×16，总的时间复杂度约为16×2252/11+2256×(1-2-61)259×16≈16×2252/11+2256×e-4≈2252.81次11轮SPECK128算法加密，存储复杂度约为2244×16=2248个SPECK128状态。

4 结论

本文通过分析模加法差分的扩散性质，找到了SPECK2n(2n=64,96,128)算法的7轮不可能差分区分器。并基于该区分器，给出了SPECK64/128算法和SPECK128/256算法的11轮不可能差分分析，以及SPECK 96/144算法的10轮不可能差分分析，恢复了全部主密钥。这些分析结果表明，SPECK算法具有较强抵抗不可能差分攻击的能力。下一步将对其他ARX结构分组密码算法的不可能差分分析进行研究。