空间相关信道下大规模MIMO两跳系统性能分析

王 毅,王雨晗,王玉红

(1.郑州航空工业管理学院 智能工程学院， 河南 郑州 450046；2.国家数字交换系统工程技术研究中心，河南 郑州 450002；3.河南大学 国际教育学院， 河南 开封 475001；4.陆军炮兵防空兵学院郑州校区 信息保障系，河南 郑州 450052)

0 引言

近年来，基于大规模MIMO技术的两跳中继系统吸引了无线通信业内越来越多的关注[1-9]。一方面，中继协作传输技术可有效地扩展通信覆盖区域、提升链路可靠性、改善小区边缘用户吞吐量，并且已有成熟的中继传输方案被国际标准化组织所采用[10-11]；另一方面，大规模MIMO技术以其独有的技术特性被学术界与工业界认为是5G无线通信系统中最核心的物理层关键技术之一[12-14]。通过大规模天线阵列的使用，系统的频谱效能可提升若干量级，并且只需采用低复杂度的线性信号处理方案就可近乎完美地消除用户间的干扰。基于此，业内研究人员很自然地将大规模MIMO技术与中继协作传输系统相结合，以期进一步挖掘系统性能提升潜力。

最初针对大规模MIMO中继系统研究，主要考虑利用大规模MIMO的多用户干扰消除特性，解决传统多对用户MIMO中继系统中用于消除用户间干扰时的正交视频资源开销过高或预编码/检测接收方案复杂度过高等问题[1]。文献[1]首次将大规模MIMO应用于多对用户中继系统，在中继配备大规模天线阵列条件下，采用低复杂度线性处理方案，即最大比接收/最大比发送(Maximum Ratio Combining/Maximum Ratio Transmission,MRC/MRT)和迫零接收/迫零发送(Zero-Forcing Receiving/Zero-Forcing Transmission,ZFR/ZFT)，分析得出了理想信道状态信息(Channel State Information,CSI)条件下的系统频谱效率极限性能。此后，针对大规模MIMO中继系统的性能分析、传输方案以及资源分配等内容得到了广泛的研究，并且从最初的两跳半双工单向中继系统，逐步扩展到双向中继系统以及全双工中继系统。文献[2-3]分别针对大规模MIMO半双工单向中继和双向中继系统中，基于理想CSI，推导得出了任意大但有限维天线数条件下的系统遍历速率解析表达式，并进行极限性能分析。文献[4]则在文献[2]的基础上扩展至大规模MIMO全双工双向中继系统；文献[5-6]针对大规模MIMO半双工单向中继系统，分别研究了ZFR/ZFT和MRC/MRT预编码方案下，非理想CSI估计时的系统频谱效率渐进性能和发射功率缩放率；文献[7]则针对大规模MIMO半双工和全双工中继系统，提出了2种导频叠加数据的传输方案，用于降低获取CSI时的系统开销；文献[8-9]针对大规模MIMO单向中继和双向中继系统，研究了能效准则下关于中继天线数、用户对个数以及中继发射功率和节点发射功率的资源分配问题。

值得注意的是，现有针对大规模MIMO中继系统的研究，多是基于理想的独立同分布信道条件。众所周知，在中继节点配备大规模天线阵列，由于中继节点尺寸问题，导致相邻天线间距可能无法满足独立性要求，从而以较大概率出现中继节点收发信机的天线相关性。因此在实际系统中，考虑中继节点大规模天线阵列所产生的信道空间相关性是十分必要的。

本文考虑更为普适的空间相关信道模型，对多对用户大规模MIMO两跳单向中继系统的遍历可达速率和功率缩放率进行分析。假设中继已知理想CSI，并采用ZFR/ZFT预编码方案。首先，借助确定性等价原理，推导出了遍历速率关于信道空间相关阵及典型系统参数的闭合表达式。分析了中继天线数趋于无穷大时，信源发射功率和中继发射功率缩放因子所对应的取值范围。最后，利用计算机仿真验证了所得到的结论的正确性和有效性。

文中符号说明：(·)H表示共轭转置运算，(·)T表示转置运算，tr{·}表示对矩阵求迹，{·}表示求数学期望，CN(n,R)为循环对称复高斯随机分布的随机向量且具有均值向量n和协方差阵矩阵R，|·|表示复数模或实数绝对值,‖·‖ 表示欧几里得范数,[A]i和[A]ij分别为矩阵A的第i行元素和第i行第j列元素。

1 系统模型

多对用户大规模MIMO两跳系统如图1所示，考虑一个包含K对单天线用户和一个大规模MIMO中继的通信系统，中继天线数为N，且N≫K>1。假设各用户对之间通信距离较远，路径传输损耗较大，因此，各通信用户对之间无可用直达链路，信源到信宿的通信过程需要借助中继在两跳内完成，此处假设所有用户对共享系统时频资源。

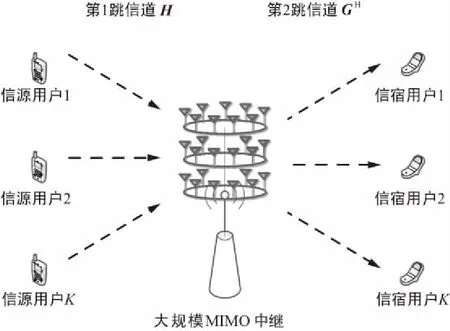
图1 多对用户大规模MIMO两跳系统

在第1跳时，K个信源用户将各自信号同时发送给中继，则中继节点的接收信号向量为：

(1)

式中，x=[x1,…,xk,…,xK]T，xk表示第k个信源用户的有效信号，且x满足发射功率归一化，即{xxH}=IK；ps表示各信源用户的平均发射功率[1-3]，H=[h1,…,hk,…,hK]∈N×K，hk表示第k个信源用户到中继之间的瑞利相关衰落信道，且表示对应的信道大尺度衰落系数，Rk表示第k个信源用户到中继接收机的信道空间相关阵，用于描述中继接收机天线间的空间相关性，则表示对应的信道快衰落系数，nr表示第1跳时叠加在中继的加性复高斯白噪声，服从分布。由于信源用户随机散落在服务区域内，此处假设不同信源用户到中继间的信道向量满足统计独立性，即hk独立于hi，i≠k。

在第2跳内，中继先对yr进行线性处理，生成转发信号yt，

yt=Vyr，

(2)

式中，V∈N×N表示中继转发处理矩阵，且满足中继总发射功率约束pr，即

tr(

(3)

随后，通过第2跳信道GH将信号yt传递至信宿用户，则K个信宿用户的接收信号向量为：

(4)

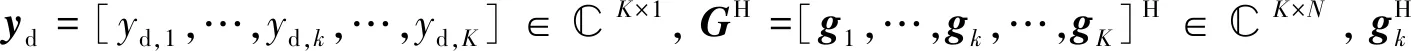
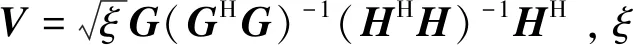
(5)

将V的具体表达式代入式(4)，可以得到第k个信宿用户的接收信号

(6)

由此得到第k个信宿用户的瞬时接收信噪比

(7)

可以得到第k个信宿用户的遍历可达速率

Rk=

(8)

式中，1/2表示两跳系统中的时隙资源开销。最终可以得到系统遍历可达和速率为：

(9)

2 可达速率渐进性能及功率缩放率

2.1 可达速率解析表达式

式(8)中的遍历速率表达式涉及期望运算，对其直接求解十分困难。与文献[5]中采用Jensen不等式求下界所不同的是本文借助随机矩阵理论中的确定性等价原理[13,17]，可以获得任意大但有限维度天线数条件下的便利速率解析表达式，有如下定理。

定理1：当中继在理想CSI条件下采用ZFR/ZFT转发方案时，第k个信宿用户的可达速率可近似表示为：

(10)

证明：根据文献[13]定理4和文献[17]定理1，有如下结论:

(11)

将式(11)中的确定性等价近似值代入式(8)，可以得到接收信噪比的确定性等价量:

(12)

进一步，根据主导理论和连续映射理论[13]，可以得到遍历速率的确定性等价量:

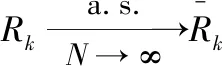
(13)

证毕。

从定理1中可知，在空间相关信道条件下，遍历可达速率仅与中继节点天线阵列的相关阵的迹有关，而信道相关阵的迹则表示信道的统计总功率值，通常进行归一化[18]，即trRk=trTk=N。由此可以看到，中继节点大规模天线阵列间的相关性并不影响遍历可达速率的绝对值。将trRk=trTk=N代入式(10)，可以进一步化简得到遍历可达速率的表达式

(14)

从式(14)可以看到，系统遍历速率与中继天线数、信源用户发射功率、中继发射功率、用户对个数以及信道的大尺度衰落因子具有直接关系。

2.2 渐进性能与功率缩放率分析

为了分析信源发射功率和中继发射功率关于中继天线数增长时可获得的缩放增益，采用如下缩放率模型[6,19]:

(15)

式中，Ps，Pr是与N无关的正常数，α，β为非负实数，分别表示信源发射功率和中继发射功率关于中继天线数的缩放增益因子。

将式(15)代入式(14)后，可以化简为：

(16)

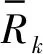
max{α-1,β-1,α+β-2}≤0，

(17)

或等价为:

0≤α≤1, 0≤β≤1。

(18)

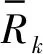
(19)

结合式(12)～式(19)，可以分析得出在空间相关信道下大规模MIMO两跳系统功率缩放时的重要结论：

① 根据式(15)并对比文献[1]中独立信道下的系统性能可知，在空间相关信道条件下，系统的可达遍历速率与可获得的功率缩放增益不受影响。换言之，在中继节点部署大规模天线阵列时，无需过分强调相邻天线的间距从而满足独立性要求，这对于大规模天线阵列用于中继节点非常有益。

② 式(19)中不同缩放因子组合值条件下的速率极限性能表明，随着中继天线数N的增加，信源用户发射功率和中继发射功率等系统参数可同时进行缩放且保持系统可达速率无损失，并且这些参数配置可适用于多种不同的系统场景需求。以典型参数设置为例，当α=1,β=1时，信源发射功率与中继发射功率进行缩放的物理意义在于，信源发射功率ps随天线数N的增加实际只需Ps/N，而中继发射功率pr实际只需Pr/N，二者实际消耗的发射功率都等比例缩小了N倍，即获得了N倍的发射功率缩放增益，此时可达速率保持在恒定值，该场景非常适用于信源和中继节点发射功率都受限的系统。当参数配置为α=0,β=1时，该场景适用于信源发射功率充足而中继发射功率受限的系统。当参数配置为α=1,β=0时，该场景则适用于中继发射功率充足，信源发射功率受限，同时需要支持大量服务用户对的场景，这对于未来5G物联网中的大规模机器类通信(massive Machine-Type Communications,mMTC)场景是非常适用的。

③ 当α<1,β<1时，系统的便利速率将呈现递增趋势，并逐渐趋向于无穷大，这主要是由于发射功率的缩放增益小于最大限度，中继天线数增长带来的遍历速率增加速度要高于发射功率缩小速度，从而保证遍历速率的持续无界增长。

④ 当α>1或者β>1时，由式(16)可知，遍历可达速率将随着中继天线数的增大而逐渐衰减为零，这主要是由于发射功率的缩放因子超出了最大限制，此时中继天线数的增加已经无法补偿发射功率的过快增长，最终将会使得可达速率衰减至零。

3 仿真结果与分析

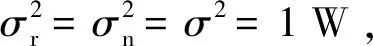
图2给出了不同用户数条件下，基于迫零传输方案的系统遍历可达和速率随中继天线数的变化趋势，仿真中设定(α,β)=(0,0)，即不考虑功率缩放增益。从仿真结果中可知，定理1中推导得出的遍历可达速率闭合表达式理论值与蒙特卡洛数值仿真结果几乎完全重合，表明理论推导值具有很好的逼近效果，这也表明所推导的解析表达式具有较好的精确性和可靠性。

图3给出了当用户对个数K=4时，在不同的功率缩放因子取值组合下，系统的遍历可达和速率随中继天线数的变化趋势。当(α,β)=(0,0)和(0.2,0.3)时，系统的遍历可达和速率随天线数增加呈近似对数线性增长，并且将逐渐趋于无穷大，主要是由于发射功率无缩放或缩放因子取值较小，中继天线数增长所带来的可达速率增益可有效地补偿发射功率降低带来的损失。当(α,β)=(1,0)，(0,1)，(1,1)时，可以看到遍历可达和速率将随着中继天线数的增加而趋近于式(19)中不同的速率极限值。同时可看到，当(α,β)在(0,0)和(1,1)之间取值时，系统遍历和速率和实际发射功率之间存在性能折中选择。一方面，当(a,b)=(0,0)时，表明系统的实际发射功率无缩减，从而大规模天线阵列所带来的阵列增益和复用增益最大，系统的和速率性能也最高；另一方面，当(a,b)取非零值时，信源和中继的实际发射功率相应缩减，大规模天线带来的阵列增益一部分用于补偿，从而对遍历速率的性能造成一定损失。特别当(α,β)=(1.5,1.6)时，显然系统遍历可达和速率出现衰减，并最终趋近于零。这主要是因为信源发射功率和/或中继发射功率的缩减倍数超过了最大限度，此时大规模天线阵列增益已不能对其等价补偿，导致系统和速率衰减为零。

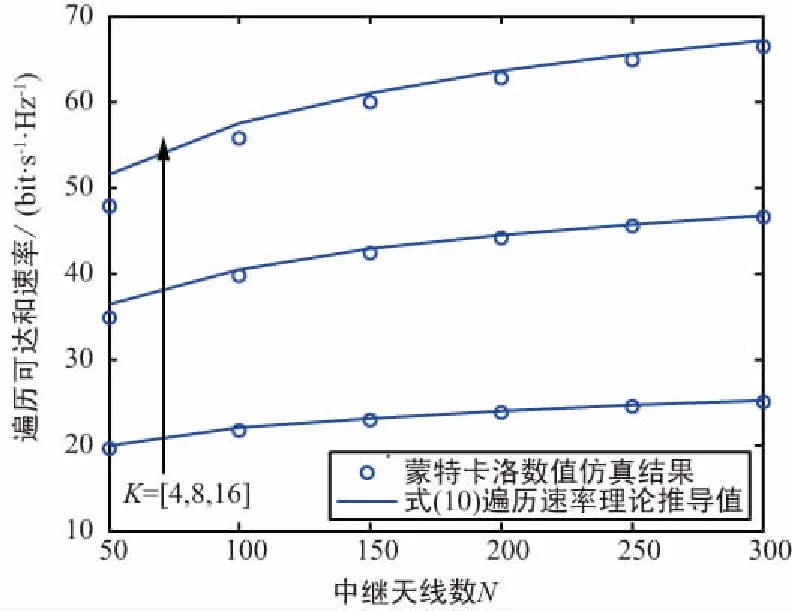
图2 不同用户对个数条件下，遍历可达和 速率随中继天线数的变化趋势

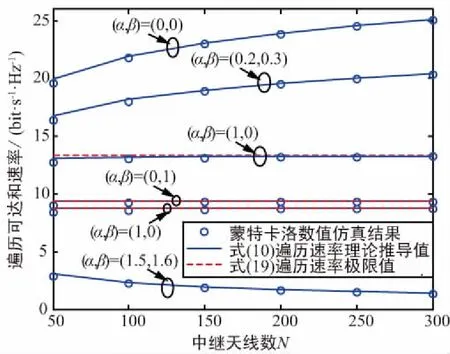
图3 不同发射功率缩放因子(α，β)组合下，遍历可达和 速率随中继天线数的变化趋势

4 结束语

本文基于空间相关信道模型，分析了迫零传输方案下多对用户大规模MIMO两跳中继系统的遍历可达速率渐进性能和功率缩放率。通过理论推导和分析，发现中继收发信机天线阵列所带来的信道空间相关性不会影响系统的遍历可达速率性能以及信源用户和中继所能获得的发射功率缩放率，这对于中继系统部署大规模天线阵列具有十分重要的指导意义。并且，针对不同的发射功率缩放因子组合值，提出了相应的适用场景，具有较好的系统设计指导意义。