基于人工智能的锂电池SOC预测建模与优化

刘聪聪，李珺凯，刘凯文，张持健

(安徽师范大学 物理与电子信息学院，安徽 芜湖 241002)

0 引言

能源紧缺与环境污染已经成为全球性的问题，自20世纪90年代以来，美国、韩国和日本等国家陆续进行了锂电池产品的研发工作，锂电池的研究和生产取得了重大发展，锂离子电池作为一种清洁能源，具备体积小、能量密度高、无记忆效应、循环寿命长及自放电率低等优势，在各个领域应用广泛[1]。

目前，锂电池作为动力能源，开始应用在越来越多的设备，例如：智能手机、数码相机、电动公交车、电动自行车及纯动力汽车等。SOC值作为衡量锂电池性能的重要参数之一，SOC值的应用为锂电池的应用奠定了基础。当大型设备应用的动力电池无法满足其性能要求时，这些动力锂电池将会被淘汰。而这种淘汰的动力电池，如果不回收处理，将会对环境造成严重污染。虽然退役锂电池不可避免存在性能衰减的现象，但是从其衰减后的剩余容量及容量衰减率看，退役锂电池的剩余容量能达到80%以上[2]，完全可以满足其他小型设备的使用需求。因此，退役后的锂电池具有较为理想的梯次利用价值。退役锂电池负载放电过程中，通过实时监测电池外部特性 (如电流、电压等)并估算锂电池剩余电量，一方面能最大限度发挥电池的性能，大大提高了退役电池能量利用率[3]，另一方法解决了退役锂电池带来的环境污染问题。

目前，常见的锂电池SOC预测方法有以下几种：① 放电实验法；② 开路电压法；③ 累积法；④ 内阻测量法；⑤ 神经网络法；⑥ 卡尔曼滤波算法[4-9]。文献[10]采用传统的神经网络法去预测电池的SOC值，但是该方法在数学模型和预测精度上存在不足；文献[11]采用扩展卡尔曼滤波法对锂电池SOC进行预测，其精度在5%；文献[12]采用LM算法改进BP神经网络对不同倍率下锂电池放电SOC预测精度有6%，误差较大；文献[13]提出在电池充放电过程对锂电池的SOC值进行修正，有效地消除了极化内阻对锂电池SOC估算的影响。以上方法虽然结果较好，但主要针对全新锂电池的非线性特性所做的研究，实际应用于退役锂电池无法获得好的结果，而退役锂电池非线性变化较强，经过长期充放电后，容量会有所下降，其内部特性发生了变化，无法表现出无全新电池一样的充放电特性，充放电效率会有所下降，用现有的模型去预测其SOC值的准确度也会降低。因此，研究一种新的满足退役锂电池特殊性的锂电池SOC动态模型具有很大的必要性。针对退役锂电池充放电过程中特殊的非线性关系，本文采用自适应法和LM算法相结合优化BP神经网络对退役锂电池SOC预测，以提高网络的收敛速度，减少系统资源占用，并在Matlab开发环境下进行仿真验证。

1 基于VLLM算法优化BP神经网络

针对退役锂电池的SOC预测较困难，与现有模型不匹配等问题，利用自适应与LM算法相结合的VLLM算法去优化BP神经网络，其预测过程收敛速度快，预测精度高。

1.1 BP神经网络

BP神经网络是一种误差反向传播神经网络，是人工神经网络的核心部分。现有的神经网络模型大部分为标准BP神经网络模型的变化或改进形式，在模式识别、故障检测和线性拟合等领域广泛应用。BP神经网络主要包含以下3个部分：输入层、隐含层和输出层。BP神经网络层与层的神经元之间一般采用全连接的方式，同一层次神经元不存在相互连接。在BP神经网络的隐含层中，神经元的激活函数选用Sigmoid函数，输出层所用的传递函数分为线性函数和非线性函数，大部分情况下会选用purlin作为线性传递函数。在改进的BP网络模型中，训练样本输入到网络模型中，逐层向后传播，计算输出结果均方误差后，如果误差未达到期望要求，则将误差值沿着各连接层逐层传递，对各层次的连接权值进行修正和调整，往误差减小的方法不断学习[14]。退役锂电池预测模型结构如图1所示。

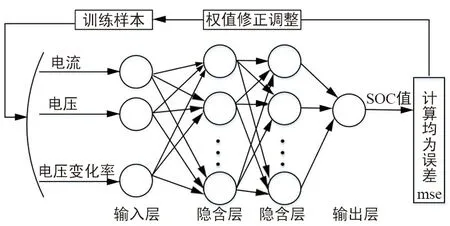
图1 预测模型结构

1.1.1 输入层模型

退役锂电池SOC值无法通过测试获得，可通过其他参数，如：电压、电流和内阻等推算获得，并且退役锂电池SOC是锂电池放电过程中剩余容量非常重要的特征参数。网络模型的输入为退役锂电池SOC预测样本集的集合，在控制实验室温度为恒温的情况下，考虑退役锂电池电压变化的特殊性，本文的输入层包括3个主要影响参数：① 退役锂电池放电电流；② 退役锂电池放电电压；③ 退役锂电池放电过程电压的变化率。由退役锂电池模型应用要求确定输入层的神经元个数为3。

1.1.2 隐层单元节点数

隐含层节点个数选取是一个特别复杂的问题，隐含层节点个数过多或过少都会对网络带来影响，导致网络训练时间增加或网络泛化能力不足。隐含层节点数的确定目前尚缺少专业的理论指导，根据经验可参照以下公式进行设计：

(1)

式中，M为隐含层节点数，m为输入节点数，n为输出节点数，a为0～10之间的调节常数。

通过上式确定的隐含层结点范围为2～11和实际训练效果确定，当隐含层节点个数为8个时，此时效果最佳。同时，由于退役锂电池具有特殊性，其随机工况SOC预测更为复杂，因此，隐含层确定为2层，隐含层神经元个数为8和17。

1.1.3 输出层模型

输出层的输出结果为退役锂电池SOC的预测值，因此，只需要1个输出层节点。

1.2 VLLM算法优化网络模型

由于退役锂电池的随机工况具有特殊性，有以下缺点：① 学习效率低； ② 网络收敛所需时间长；③ 参数选择较敏感；④ 网络结构选择不一致；⑤ 新样本加入，影响已学习样本。因此，本文提出一种VLBP算法和LM算法相结合的VLLM(Var-iable Learning Levenberg Marquardt)算法来弥补标准BP算法的不足,分别对网络的权值、阈值和收敛速度等进行优化，使电池SOC预测精度较高的情况下收敛速度也较快。

1.2.1 LM算法原理

LM算法[15-17]是针对中等规模的前馈神经网络提出的快速算法，可以提升网络的收敛速度。Hecht-Nielsen证明得出的Kolmogorov 定理：任意一个3 层前馈网络能够实现对任意连续函数的最佳逼近。LM算法具体对网络训练的过程分为:

① 误差计算公式如下：

(2)

式中，Xi为期望输出，Yi为实际输出。

② LM 算法的网络权值修正式如下：

ω(h+1)=ω(h)-[JTJ+μI]-1JTe，

(3)

式中，ω(h+1)为经过修正调整后的连接权值，ω(h)为现在的网络连接权值，J为雅克比矩阵，μ为一个非负数，通过调整μ值，可以有效地避免误差较大或较小。前馈神经网络计算Hessian矩阵非常复杂，LM算法避免了求Hessian矩阵，减少了网络计算成本，相比较标准BP算法，LM算法能获得最快的收敛速度，但网络权值数量增加时，LM算法的优势将逐渐变得不明显，且其存储空间需求较大。

1.2.2 可变学习因子优化BP网络模型

虽然LM算法能优化网络的精度，但其内存占用较大，所需训练时间增加。由于训练的不同阶段，所需要的学习率的值不同，自适应算法能调整学习率的值，提高算法的性能和稳定性。因此，提出自适应学习率算法和LM算法结合，使退役锂电池SOC预测精度较高的情况下收敛速度也较快。

为实现快速有效的学习收敛过程，TPVogl等人提出了一种可变学习因子的BP算法(V-ariable Learning Rate Back Propagation,VLBP)[18]。VLBP算法是通过观察误差的增减来判断。如果误差逐渐减小趋于目标值时，学习速率乘以一个增量因子；如果相反，则学习速率乘以一个减量因子。式(4)给出了可变学习因子修正学习速率的表达式：

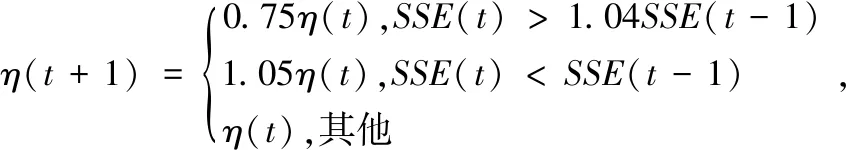
(4)

式中，η为学习速率，t为训练次数，SSE为误差函数。

1.2.3 VLLM优化BP网络算法流程

VLLM优化BP网络算法流程如图2所示。

图2 VLLM优化BP网络算法流程图

2 SOC预测及结果分析

2.1 参数归一化

为了避免出现训练样本中小数值的有用信息被大数值的信息吞噬现象，在将训练样本输入网络模型之前，要对其所有数据进行归一化处理，通过不同的归一化方法，将各输入样本归一到[0,1]区间。本文用以下方法对输入样本进行了归一化处理，公式如下：

(5)

式中，a，b为常量，xmax，xmin为训练样本每组变量的最大值和最小值，x，xi′为归一化前后的值，且xi′∈[xmin，xmax]。

2.2 电芯测试

以3.7 V/2 000 mAh的18650锂电池为研究对象，在恒温条件下采用新威尔型号为CT-4008的高精度电池性能测试系统进行充放电实验采集原始数据，实验中分别对18650电池以0.2C，0.5C，1C，2C的倍率放电，对应电流为0.4 A,1 A,2 A,4 A对电池进行放电测试。样本采集和选取完毕后，并将样本数据导入到优化后神经网络动态模型中去训练和验证，利用MATLAB现有的工具箱来建立退役锂电池SOC预测模型，将训练样本进行归一化处理后，输入到网络模型中，采用VLLM算法来对网络的连接权值不断进行调整修正，输出退役锂电池不同放电倍率下的SOC预测值，其中训练目标误差取10-4。

改进算法的SOC误差对比曲线如图3所示，VLLM算法放电t-SOC曲线如图4所示，VLLM算法OCV-SOC曲线如图5所示，不同倍率放电下SOC预测结果如图6所示。

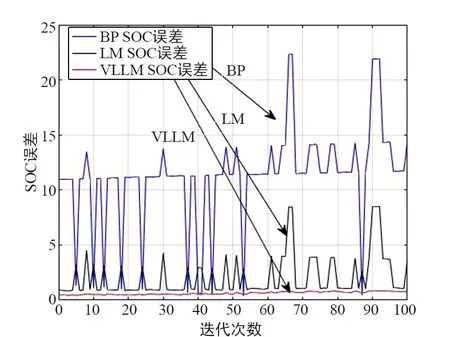
图3 改进算法的SOC误差对比曲线

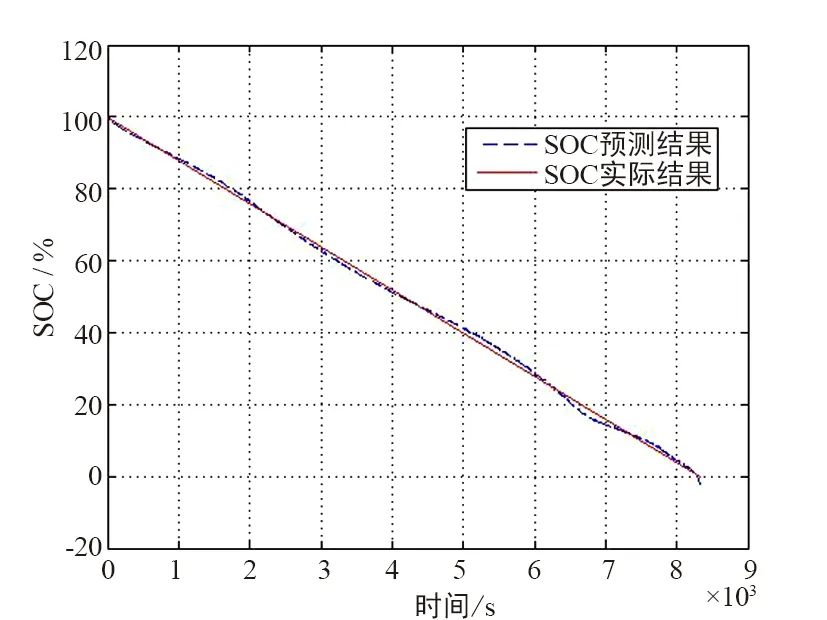
图4 VLLM算法放电t-SOC曲线

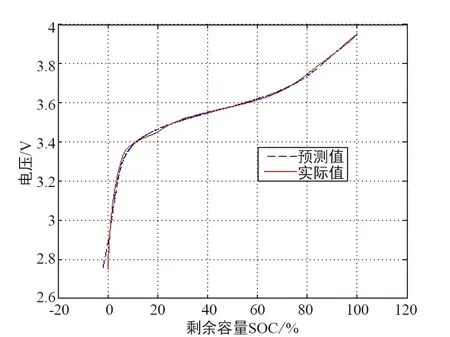
图5 VLLM算法OCV-SOC曲线

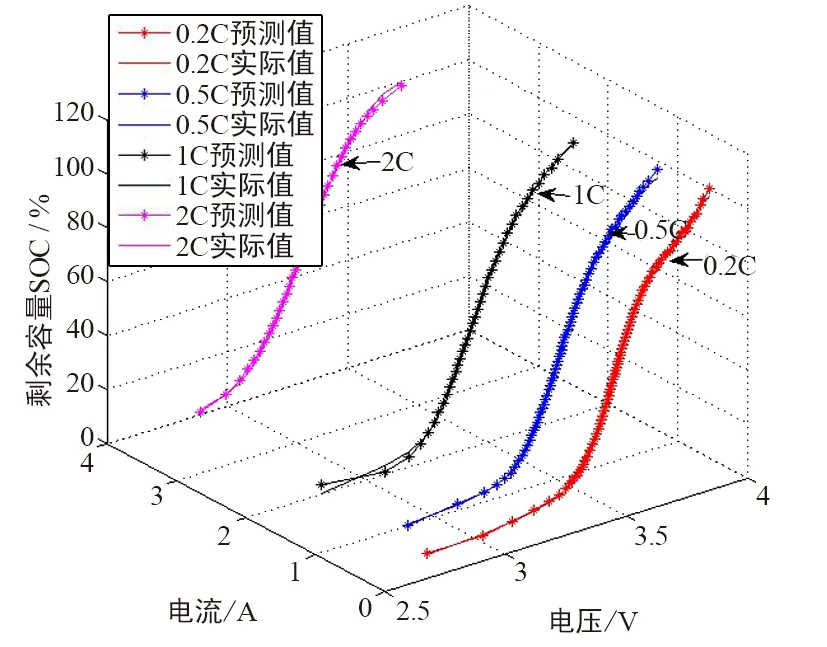
图6 不同倍率放电下SOC预测结果

2.3 随机工况测试

此外，利用随机工况模拟电池放电过程中，由于外部因素造成的电流变化情况，进行了随机工况退役锂电池SOC预测。针对退役电池的特殊非线性，在模拟实际工况的随机工况实验中，分别以0.2C，0.5C，1C，2C的倍率进行随机时间放电测试，其电流、电压结果如图7和图8所示。

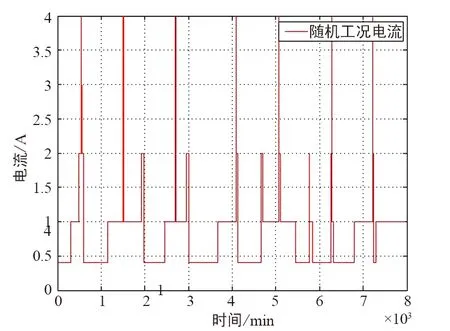
图7 随机工况电流

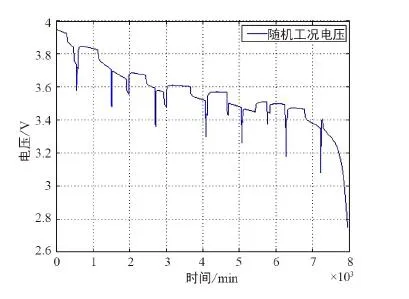
图8 随机工况电压

随机工况过程预测相对标准工况具有更大的复杂度，随机工况利用改进的VLLM模型与利用现有BP网络模型的测试结果相比较，误差可以由11%左右降到5%左右，预测精度有很大的提升，为退役锂电池的梯次利用奠定了基础。

未优化和优化的随机工况放电t-SOC曲线如图9和图10所示，未优化和优化的随机工况SOC预测误差如图11和图12所示，随机工况的SOC预测拟合结果如图13所示。

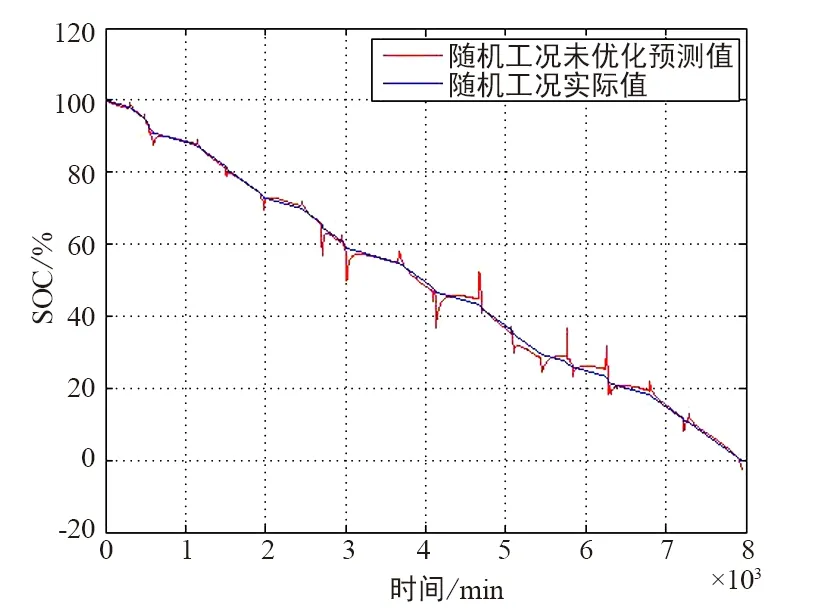
图9 随机工况放电t-SOC曲线(未优化)

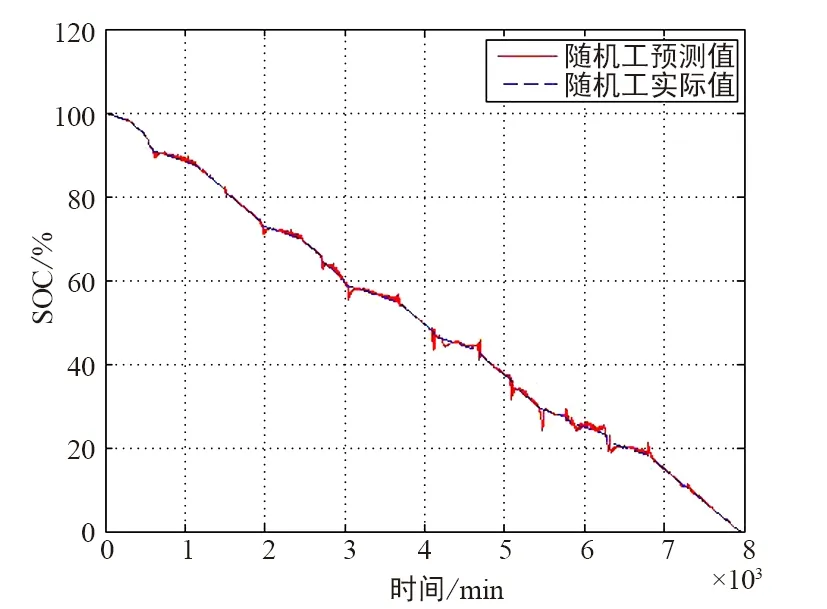
图10 随机工况放电t-SOC曲线(优化)

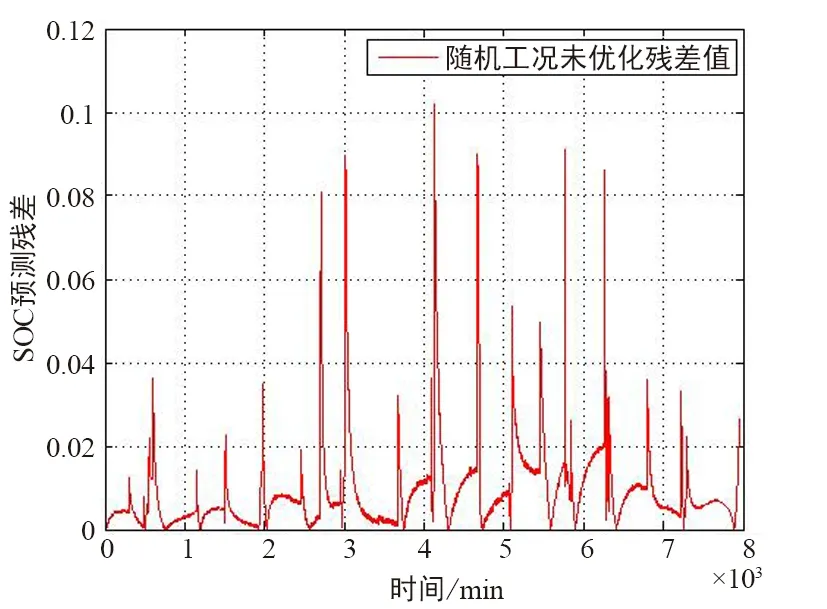
图11 随机工况SOC预测误差(未优化)

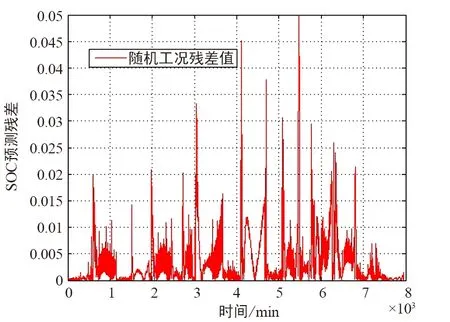
图12 随机工况SOC预测误差(优化)

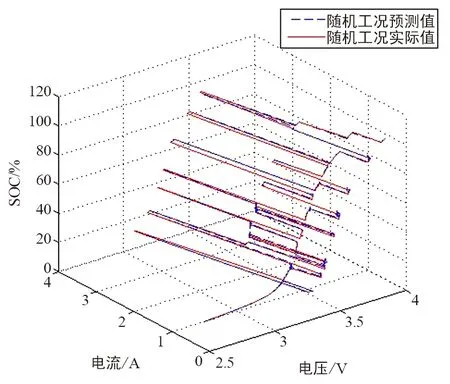
图13 随机工况的SOC预测拟合结果

3 结束语

本文在控制放电温度为恒温的情况下，分析以往的锂电池SOC预测方法以及退役锂电池SOC值的特殊非线性关系，在算法和结构上对BP网络模型进行了改进，提出自适应学习率与LM算法相结合的VLLM算法，训练改进BP神经网络在退役锂电池SOC预测上的应用。通过3种算法的对比，证明了VLLM算法训练结果更佳。结果显示，其预测误差不超过1%，并且在模拟实际工况的随机工况实验中，其误差在5%以内，满足国家动力电池检测标准，证明此方法具有很大的应用前景。