基于威布尔分布杂波模型的加权有序统计模糊CFAR检测算法
2019-04-23王陆林刘贵如
王陆林,刘贵如,邹 姗
(安徽工程大学 计算机与信息学院,安徽 芜湖 241000)
0 引 言
恒虚警率(constant false alarm rate,CFAR)检测通过将待检测单元与功率检测门限进行比较,判断目标有无。功率检测门限通常由背景噪声功率估计值乘以检测门限系数,该系数通常与目标恒虚警率有关。在不同的应用场景中,雷达散射回波信号可以通过由概率密度函数表征的统计模型表示,如瑞利分布杂波模型[1-2]。恒虚警率检测算法目前比较常见的是基于单元平均的恒虚警率(cell averaging constant false alarm rate, CA-CFAR)[3]检测算法和基于有序统计的恒虚警率(order statistic constant false alarm rate, OS-CFAR)检测算法[4]以及相关的组合,应用于不同杂波和多目标干扰环境下。背景噪声功率的准确估计,离不开杂波分布模型[5]。多年来,瑞利分布作为比较常见的杂波分布模型得到了广泛的应用。但是针对高分辨率雷达系统,在大部分实际应用场景中,雷达回波中的杂波信号分布偏离瑞利分布,呈现威布尔分布[6]。威布尔分布模型很好地描述了由地面和海水表面动态反射回波,尤其是高频雷达在水平夹角相对较小的情况下。威布尔分布模型包含2个参数:①比例参数,一般用λ表示,与背景噪声功率均值密切相关;②形状参数,一般用γ表示,与模型概率密度函数的偏度有关。
过去许多专家学者对基于威布尔分布杂波模型的CFAR检测算法进行了深入研究。通过极大似然估计(maximum likelihood, ML)或者有序统计估计(ordered statistics, OS)得到模型的比例参数和形状参数,从而得到自适应功率检测门限[7]。OS-CFAR检测器[8]与极大似然恒虚警率(maximum likelihood-constant false alarm rate, ML-CFAR)检测器相比,结构比较单一,在杂波干扰环境下,作为背景噪声功率估计值的参考单元选择不合理的情况下,会造成较大的检测损失或者过多的虚警。针对这种问题,Elias等[9]结合OS-CFAR和最大选择恒虚警率(greatest of-constant false alarm rate, GO-CFAR)检测算法和最小选择恒虚警率(smallest of-constant false alarm rate, SO-CFAR)检测算法的特点提出了有序统计最大选择恒虚警率(order statistic greatest of-constant false alarm rate, OSGO-CFAR)和有序统计最小选择恒虚警率(order statistic smallest of-constant false alarm rate, OSSO-CFAR)检测器。OSGO-CFAR检测器在杂波边缘干扰环境下具有较低的虚警率。而OSSO-CFAR检测器在多目标干扰环境下具有较高的检测率,检测损失较小。但是在均匀噪声环境下,OSGO-CFAR和OSSO-CFAR检测器检测损失较大,检测性能严重下降[9]。
为了使得OSGO-CFAR和OSSO-CFAR检测器能够在均匀和非均匀噪声环境下均具有较好和较稳定的检测性能,本文在充分研究威布尔分布杂波模型的基础上,引入了基于模糊逻辑的软规则,提出一种基于威布尔分布杂波模型的加权有序统计模糊恒虚警(weighted order statistic and fuzzy-constant false alarm rate,WOSF-CFAR)检测算法,通过计算 Leading和Lagging子窗口对应的模糊隶属函数值,并采用了代数积、代数和、最大选择和最小选择4种融合规则对2个子窗口的模糊输出量进行融合,并与比较门限进行比较,判别目标有无,有效提高了噪声功率估计的精度和自适应性。通过与OSGO-CFAR和OSSO-CFAR检测算法进行仿真比较,WOSF-CFAR检测算法在均匀和非均匀杂波噪声环境下均具有较好的检测性能。
1 相关问题描述
在检测系统中,系统接收由观测对象反射回的回波信号经过检波器后得到若干观测单元。每个观测单元通过预先设定的假设比较判断是否为有效目标的回波信号单元[10-11]。比如大部分的雷达检测系统中,假设H1表示有目标,H0表示无目标。则在假设无目标的情况下,观测单元中认为只包括有噪声单元、杂波干扰单元。如果假设为有目标,则观测单元中认为不仅包括噪声单元、杂波干扰单元外,还包括有效目标的回波信号单元。传统的CFAR检测系统,回波信号通常经过检波器后得到输出序列存储在缓冲池中作为算法的输入参考单元。其中,用于目标检测的参考单元称为待检测单元。每个参考单元相互独立。假设X0表示待检测参考单元,T表示检测门限。则有无目标的判决表示为
X0>T⟹H1;X0 (1) 在雷达检测系统中,通常需要保证恒定的虚警率记为Pfa。如果回波中杂波分布状态可知或者可预知,则检测门限T比较容易估计,而且容易保持恒定的虚警率。但是在实际的应用场景中,尤其是动态环境下,杂波分布及其参数不断变化,此时采用固定的检测门限无法保证恒定的虚警率[12]。CFAR检测系统通常的做法是通过取检测参考单元周围的参考单元组成参考窗,通过参考窗中的参考单元实时估计背景噪声功率并调整功率检测门限T,将Pfa保持在一定范围内[13]。威布尔杂波模型能够很好地描述海杂波和地面后向散射回波杂波信号的分布特性。其概率密度函数记为pdf,表示为 (2) (2)式中:λ为随机变量x的比例参数;γ为随机变量x的形状参数。λ参数与当前回波的实时功率有关,会随着回波功率的变化而变化;γ参数与回波反射面的形状即物理特性和几何尺寸有关。一般为了简化,假设γ为已知,与参考窗中参考单元数量有关。检测门限T可以表示为 (3) (4) 在设定Pfa的情况下,γ为已知,通过仿真可以确定。此时只需要通过参考窗中的参考单元记为Xi(i=1,2,3,…,N),估计参数λ即可进行目标的有无判别,基于威布尔分布模型的CFAR检测器原理框图如图1所示。图1中,待检测参考单元X0左边为子参考窗口Leading window记为A,右边子参考窗口Lagging window记为B。 图1 基于威布尔分布模型的CFAR检测器Fig.1 CFAR detector in the Weibull distribution model 在OS-CFAR检测器当中,首先需要对参考窗中所有参考单元按照功率值进行升序排列,然后选择第k个参考单元记为Xk,1≤k≤N,用于估计参数λ。其目标有无判别方法表示为 (5) 在OSGO-CFAR检测器中,分别从子参考窗中选择第k个参考单元,记为Xak和Xbk,其中,1≤ak≤N/2,1≤bk≤N/2。然后选择较大的用于估计参数λ,其目标有无判别方法表示为 (6) 还可以简化为 (7) 在OSSO-CFAR检测器中,分别从子参考窗中选择第k个参考单元,记为Xak和Xbk,其中,1≤ak≤N/2,1≤bk≤N/2。然后选择较小的用于估计参数λ,其目标有无判别方法表示为 (8) 还可以简化为 (9) 假设f(Pfa)1/γ=G,针对OS-CFAR检测器,虚警率Pfa可以表示为[14] (10) (10)式中,Γ(·) 为伽马函数。 针对OSGO-CFAR检测器,Pfa可以表示为[15] (11) 针对OSSO-CFAR检测器,Pfa可以表示为[15] (12) 假设信噪比记为S,将(10)式中的Gγ替换为G2/(1+S),即可得到OS-CFAR的检测率Pd可以表示为 (13) 将(11)式中的Gγ替换为G2/(1+S),即可得到OSGO-CFAR的检测率Pd可以表示为 (14) 将(12)式中的Gγ替换为G2/(1+S),即可得到OSSO-CFAR的检测率Pd可以表示为 (15) OSGO-CFAR和OSSO-CFAR检测器只所以在均匀噪声环境下检测损失较大,检测性能严重下降,主要原因是对子参考窗A和B之间选择时进行了二元判决,造成了大量信息的丢失。本文引入了基于模糊逻辑的软规则,取代了二元判决,避免了信息损失,可以有效提高检测器的检测性能。 假设X0/Xak=z1X0/Xbk=z2,则OSGO-CFAR和OSSO-CFAR检测器目标有无判决可以表示为 f(z1,z2)=α·z1+βz2>f(Pfa)1/γ⟹H1 f(z1,z2)=α·z1+βz2 (16) (16)式中:α,β为加权系数。针对OSGO-CFAR,如果z1≤z2,则α=1,β=0,否则α=0,β=1;针对OSSO-CFAR,如果z1≥z2,则α=1,β=0,否则α=0,β=1。通常情况下,加权系数为离散值,会导致信息的丢失。为此,引入了软权重函数w(zi),i=1,2。在假设无目标H0时,可以得到模糊隶属函数,并在[0,1]服从均匀分布。模糊隶属函数表示为 w(zi)=Pr(z>zi|H0)=1-FZ(zi),i=1,2 (17) (17)式中,z为随机变量,z=X0/XkXk∈{Xak,Xbk},FZ(zi),i=1,2为随机变量z的积累分布函数;w(zi),i=1,2表示在假设无目标的情况下,z=X0/Xk大于比较门限zi,i=1,2的概率,w(zi)将观测空间映射到与目标虚警率Pfa相关的虚警空间。 假设X0和Xak或者Xbk的概率密度函数分别表示为fX(·) 和fxk(·)。则z的概率密度函数可以表示为 (18) Xak或者Xbk的概率密度函数可以表示为 (19) (19)式中,Fx(x) 为威布尔累积分布函数。将(2)式和(19)式代入(18)式,得到z的概率密度函数fZ(zi)表示为 (20) z的累积分布函数FZ(zi)表示为 (21) (21)式代入(17)式可得模糊隶属函数w(zi)为 (22) (22)式中,如果将zi替换为G,(22)式就表示有N/2个参考单元的的OS-CFAR的Pfa。(22)式表示OS-CFAR中,子参考窗A和B的模糊隶属函数w(zi),i=1,2。为了根据2个子参考窗的模糊隶属函数值进行最终有无目标的判决,引入了几种融合方法,分别是“Algebraic product,AP” “Algebraic sum, AS”“Maximum”和“Minimum”。因为模糊隶属函数w(zi)为单调递减函数,假设f(w(z1),w(z2))表示模糊隶属函数经过融合后的最终输出值。基于威布尔分布模型的WOSF-CFAR检测器原理框图如图2。 图2 基于威布尔分布模型的WOSF-CFAR检测器Fig.2 WOSF-CFAR detector in the weibull distribution mode f(w(z1),w(z2)) f(w(z1),w(z2))>G⟹H0 (23) 因为f(Pfa)1/γ=G,所以G可以根据Pfa以及参数γ进行计算得到判决比较门限。当采用“Algebraic product”融合规则对子参考窗A和B中的模糊隶属函数值w(z1)和w(z2)进行融合时,融合后的输出值f(w(z1),w(z2))表示为 f(w(z1),w(z2))=w(z1)×w(z2) (24) 当采用“Algebraic sum”融合规则对子参考窗A和B中的模糊隶属函数值w(z1)和w(z2)进行融合时,融合后的输出值f(w(z1),w(z2))表示为 f(w(z1),w(z2))=w(z1)+w(z2)-w(z1)×w(z2) (25) 当采用“Maximum”融合规则对子参考窗A和B中的模糊隶属函数值w(z1)和w(z2)进行融合时,融合后的输出值f(w(z1),w(z2))表示为 f(w(z1),w(z2))=max{w(z1),w(z2)} (26) 对比(7)式可以看出,采用“Maximum”融合规则时,WOSF-CFAR检测算法的检测原理和OSGO-CFAR检测算法相似。 当采用“Minimum”融合规则对子参考窗A和B中的模糊隶属函数值w(z1)和w(z2)进行融合时,融合后的输出值f(w(z1),w(z2))表示为 f(w(z1),w(z2))=min{w(z1),w(z2)} (27) 对比(8)式可以看出,采用“Minimum”融合规则时,WOSF-CFAR检测算法的检测原理和OSSO-CFAR检测算法相似。 本文在Matlab环境下,采用蒙特卡洛仿真方法,通过SwerlingⅠ和SwerlingⅡ起伏目标模拟非均匀噪声环境。对所提出的WOSF-CFAR检测算法的检测性能进行仿真。在各信杂比(signal-to-clutter power ratio, SCR)条件下进行检测性能对比,假设目标虚警率Pf=10-4,参考窗长度N=24。在以下仿真对比分析图中,采用“Algebraic Product”融合规则的WOSF-CFAR检测结果曲线用AP表示;采用“Algebraic Sum”融合规则的WOSF-CFAR检测结果曲线用AS表示;采用“Minimu”融合规则的WOSF-CFAR检测结果曲线用Min表示;采用“Maximum”融合规则的WOSF-CFAR检测结果曲线用Max表示。 图3为形状参数γ分别为0.4,0.8时,WOSF-CFAR算法针对各融合规则,在均匀噪声环境下的检测性能对比结果。通过图3可知,相同信杂比条件下,形参γ越大,检测率Pd越高。相同形参γ条件下,采用AP融合规则时,WOSF-CFAR检测算法检测率最高,采用Min融合规则时,WOSF-CFAR检测算法检测率最低。采用AS和Max融合规则时检测性能相当。另外,在均匀噪声环境下,采用Max和Min融合规则时,WOSF-CFAR算法检测性能分别与OSGO-CFAR和OSSO-CFAR算法检测性能相当。但是采用AP和AS融合规则时,WOSF-CFAR算法检测性能优于OSGO-CFAR和OSSO-CFAR算法的检测性能。 图3 均匀噪声环境下,当γ=0.4,0.8时,WOSF-CFAR检测器的检测性能Fig.3 Pd of the WOSF-CFAR detector in homogenous environments for γ=0.4,0.8 图4为形状参数γ=0.4时WOSF-CFAR算法针对各融合规则,在多目标干扰环境下,干扰目标单元出现在Lagging或者Leading子窗口中时的检测性能对比结果。通过图4可知,采用AP融合规则时,WOSF-CFAR检测算法检测率最高;采用Max融合规则时,WOSF-CFAR检测算法检测率最低。采用Min融合规则时检测性能优于采用AS融合规则时的检测性能,因为当干扰目标单元出现在子参考窗B中时,通过最小选择选择了子参考窗A中的隶属函数值参与计算比较,相对于采用AS融合规则时,检测率相对较高。而采用Max融合规则时,取子参考窗B中的隶属函数值参与计算比较,检测率降低。采用AP融合规则时,得到的隶属函数值f(w(z1),w(z2))最小,所以WOSF-CFAR检测算法检测率最高。采用AP融合规则时,WOSF-CFAR算法检测性能优于OSGO-CFAR和OSSO-CFAR算法的检测性能。 图5为形状参数γ=0.4时WOSF-CFAR算法针对各融合规则,在多目标干扰环境下,干扰目标单元同时出现在Lagging和Leading子窗口中时的检测性能对比结果。 通过图5可知,采用AP融合规则时,计算得到的隶属函数值f(w(z1),w(z2))最小,所以此时WOSF-CFAR检测算法检测率最高;采用Min融合规则时,计算得到的隶属函数值f(w(z1),w(z2))最大,此时WOSF-CFAR检测算法检测率最低。采用AS融合规则时,通过取均值,计算得到的隶属函数值f(w(z1),w(z2))相对小于采用Max融合规则时的隶属函数值,故检测率相对较高。 图4 当干扰目标单元出现在子参考窗B中时,WOSF-CFAR检测器的检测性能Fig.4 Pd of the WOSF-CFAR detector in interfering targets within lagging window B for γ=0.4 图5 当干扰目标单元同时出现在子参考窗A和B中时,WOSF-CFAR检测器的检测性能Fig.5 Pd of the WOSF-CFAR detector in interfering targetswithin lagging A and leading window B for γ=0.4 从图4、图5中可以看出,在多目标干扰环境下,采用Max和Min融合规则时,WOSF-CFAR检测算法的检测性能分别与OSGO-CFAR和OSSO-CFAR检测算法的检测性能相当。但是采用AP和AS融合规则时,WOSF-CFAR算法的检测性能优于OSGO-CFAR和OSSO-CFAR算法的检测性能。 图6为采用AP融合规则时,WOSF-CFAR算法在多个干扰目标环境下的检测率。从图6中可以看出,采用AP融合规则时,WOSF-CFAR算法的检测性能随着干扰目标数的增加,检测性能逐渐下降,但当干扰目标数I≥3时,检测性能趋于稳定。 图6 当γ=0.4,多目标干扰环境下,采用AP融合规则时,WOSF-CFAR检测器的检测性能Fig.6 Pd of the WOSF-CFAR detector in multi-interfering targets environments with AP fusion rule for γ=0.4 图7为采用Max融合规则时,WOSF-CFAR检测算法在多个干扰目标环境下的检测率。 从图7中可以看出,采用Max融合规则时,WOSF-CFAR检测算法的检测性能随着干扰目标数的增加,检测性能逐渐下降,但当干扰目标数I≥3时,检测率趋于0。 图7 当γ=0.4,多目标干扰环境下,采用Max融合规则时,WOSF-CFAR检测器的检测性能Fig.7 Pd of the WOSF-CFAR detector in multi-interferingtargets environments with Max fusion rule for γ=0.4 图8为WOSF-CFAR检测算法针对各融合规则,在杂波干扰环境下的虚警率控制对比曲线。从图8中可以看出,当杂波干扰单元个数Nc≤5时,采用Min融合规则时,WOSF-CFAR检测算法的虚警率控制效果最优;采用Max融合规则时,虚警率控制效果最差;采用AP融合规则时,虚警率控制效果优于采用AS融合规则时的虚警率控制效果。当杂波干扰单元个数Nc>5时,采用Max融合规则时,WOSF-CFAR检测算法的虚警率控制效果最优;采用Min融合规则时,WOSF-CFAR检测算法的虚警率控制效果最差;采用AS融合规则时,虚警率控制效果优于采用AP融合规则时的虚警率控制效果。另外,在杂波干扰环境下,采用Max和Min融合规则时,WOSF-CFAR检测算法的虚警率控制效果分别与OSGO-CFAR和OSSO-CFAR检测算法的虚警率控制效果相当。 图8 杂波干扰环境下,采用各融合规则时WOSF-CFAR的虚警率Fig.8 Pfa of the WOSF-CFAR detector in clutter edgesinterference environments with each fusion rule 从图3—图7中可以看出,当目标虚警率Pfa设置较大时,WOSF-CFAR检测器的检测损失较小。在实际目标检测过程中,为了提高检测率,尽可能地使得Pfa采接近于目标虚警率,同时降低目标遮挡效应。另外采用AP融合规则时,WOSF-CFAR检测算法的检测性能最优。 本文首先对传统的OS-CFAR,OSGO-CFAR和OSSO-CFAR检测算法进行了理论分析,结合基于威布尔分布的CFAR检测器给出了目标有无的判别方法。为了克服以上算法采用二元判决导致大量信息丢失的问题,本文借鉴了分布式CFAR检测算法的优点,引入了模糊逻辑,提出了一种加权有序统计模糊恒虚警 (WOSF-CFAR) 检测算法,并采用了代数积(AP)、代数和(AS)、最大选择(Max)和最小选择(Min)融合规则对2个子窗口的模糊输出量进行融合后与比较门限进行目标有无的判决。仿真结果表明,与以上3种算法相比,WOSF-CFAR检测算法检测性能有很大的提升,尤其是采用代数积融合规则时,检测性能最优。而采用最大最小融合规则时,其检测性能与OSGO-CFAR和OSSO-CFAR检测性能相当。本文只针对形参γ取几种典型值时的检测性能进行了仿真分析,后续将深入研究各个实际应用场景下,形参γ对WOSF-CFAR算法检测性能的影响,使得算法在实际工程应用中得到最优的检测性能。
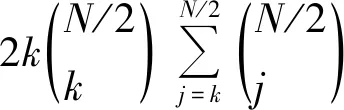
2 WOSF-CFAR检测器


3 仿真分析






4 结 论
