库水位涨落和降雨入渗对岸坡浸润线的影响分析
2019-04-23张泽东
张泽东
(新疆吉木萨尔城镇水管所,新疆 吉木萨尔 831700)
库水位涨落和降雨入渗是影响水库库岸边坡稳定并引起岸坡滑坡的重要原因,统计资料显示,日本大约有65%的水库滑坡出现在库水位骤降期间,其余35%则发生在库水位上升时期,而《中国典型滑坡》中所列举的水库滑坡案例至少有90%与库水位涨落和降雨密切相关,可见,研究库水位涨落、降雨以及库水位涨落和降雨联合作用对库岸浸润线的影响,进而研究水库岸坡浸润线位置对滑坡稳定性的影响对于岸坡稳定性意义重大。近年来,国内外大量学者运用数值方法进行了地下水浸润线的研究,如吴越,陆新等基于有限差分法进行了库水位涨落和降雨入渗联合作用的工况下滑坡过程中地下水位的计算[1];林志红,项伟等运用饱和渗流模型和非饱和渗流模型进行了库水位涨落对浸润线变化可能影响情况的模拟,并对降雨入渗机制进行深入探讨[2],然而数值方法原理复杂,仅适用于理论研究,在工程实际中运用较少。为此,笔者采用均质岸坡地质模型,充分考虑库水位涨落、降雨入渗以及库水位涨落和降雨入渗联合作用,进行库岸岸坡浸润线的非稳定渗流计算,并据此对岸坡浸润线变动规律进行分析。
1 岸坡浸润线计算模型
1.1 假设条件
含水层具有均质性和各向同性,无侧向延展性,底部主要是水平向非透水层,潜水流则表现为一维流态势,库水位涨落前库岸岸坡初始浸润线为H(x,0);库水位涨落范围内垂直库岸较小,则一维非稳定渗流方程为:
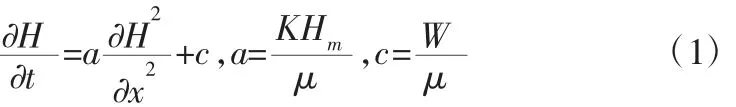
式中:α 为压力传导系数值,m2/d;Hm为含水层厚度均值,m;μ为重力给水度;K 为渗透系数,m/d;W 为降水入渗强度,m/d;c为降水有效强度,m/d;t 为降水持续时间,d。
1.2 岸坡浸润线计算模型
在初始时刻t=0 时,库岸岸坡初始浸润线为H(x,0),与库岸相距x 处的地下水位变幅为S(x,t),则t 时刻浸润线方程表示如下:
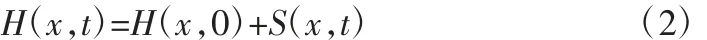
对于库水位涨落与降雨入渗的联合作用,地下水非稳定渗流模型表示如下:
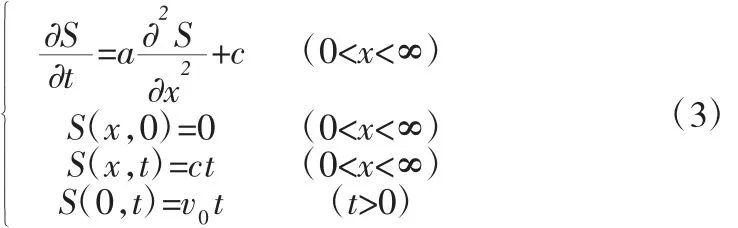
1.3 浸润线方程求解
将方程组(3)进行拉普拉斯正逆变换求解,得:
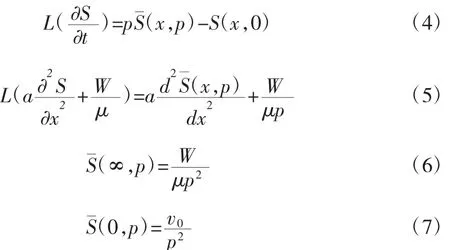
根据式(4)和(5)可知:
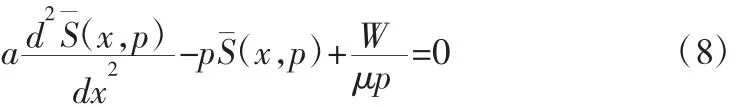
求得二阶线性齐次微分方程(8)的通解如下:

将式(6)和(7)代入式(9)可得:
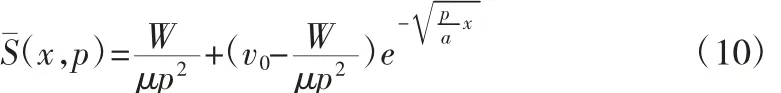
运用拉氏逆变换进行式(10)的化简,得:
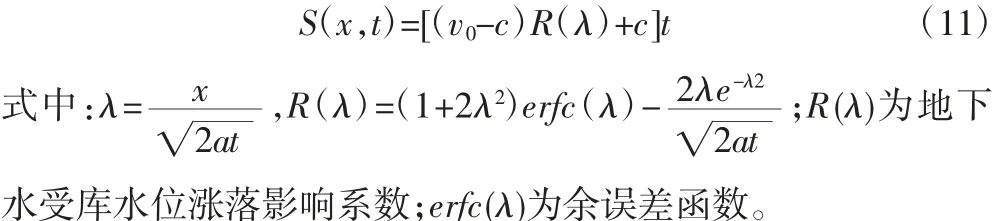
通过式(2)和(11)可以得到时刻t 库水位涨落和降雨联合作用下库岸岸坡浸润线方程[3],即:
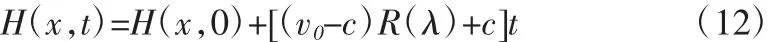
2 算例及分析
2.1 工程概况
东大龙口水库座落于吉木萨尔县吉木萨尔镇东大龙口河流的中下游,是一座以防洪、农业灌溉、城市居民供水为主的中型水库。东大龙口水库规模为中型,水库总库容1250 万m3。大坝坝型为粘土心墙土石坝,坝顶长度698 m,最大坝高35.5 m,坝顶宽5 m,坝顶高程(黄海)981.5 m。
为进行库水位涨落和降雨入渗对岸坡浸润线影响的分析,笔者结合东大龙口水库工程实际,设计库水位涨落范围为145 m~175 m,落差30 m,分析模型见图2。具体计算时采用MATLAB 分析工具绘制各种工况下岸坡浸润线的分布情况[4]。

图1 东大龙口水库工程浸润线计算模型
2.2 压力传导系数对岸坡浸润线的影响
在图1 计算模型中取L=100 m,求压力传导系数α 和下降时间不同且库水位均匀下降情况下岸坡浸润线的变动规律。由于东大龙口水库水位调度方案中水位降速最大值为2.5 m/d,故计算时假设降速v0=2.5 m/d,得到岸坡浸润线变动规律,见图2、图3。结合东大龙口水库工程实际,相同断面的岸坡水头、水力梯度与压力传导系数α 呈相反变动,考虑到库水位的作用,水力梯度呈动态变动趋势,由图2 可知,压力传导系数α随着库水位匀速下降而减小,浸润线随库水位匀速下降而变得更加陡峭。

图2 压力传导系数与浸润线关系示意图
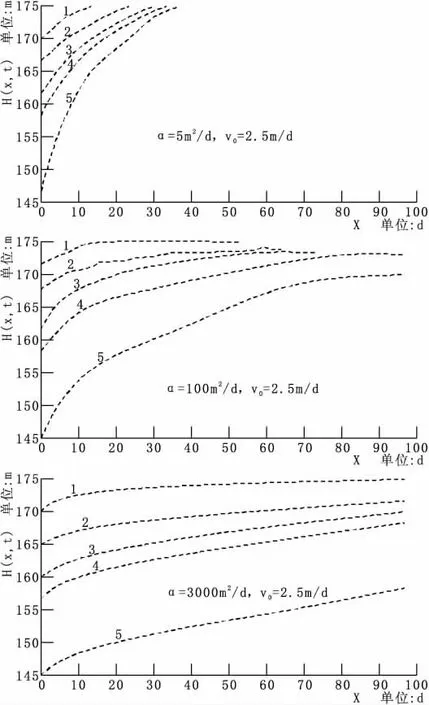
图3 压力传导系数α 不同且库水位均匀下降岸坡浸润线的变动规律
从图3 可以看出,在库水位匀降的过程中,岸坡浸润线的位置和形状变化与压力传导系数α 取值大小有关,当α<5 m2/d时,岸坡浸润线与原来位置相比并无明显变化,而且此种情况下,水力梯度与渗透力均较大,对岸坡稳定最为不利;当5 m2/d<α<3000 m2/d,岸坡浸润线呈上凸形状,水利梯度与渗透力逐渐减小;当3000 m2/d<α<4000 m2/d 时,岸坡水位与库水位同时下降,浸润线近似于倾斜的直线,变化缓和,断面水力梯度达到很小;当α>4000 m2/d 时,浸润线为水平直线,岸坡渗透力趋于零,此时已无渗流稳定性计算的必要。
2.3 库水位涨落速度对岸坡浸润线的影响
在图1 计算模型中取L=100 m,压力传导系数α=4000 m2/d,t=10 d,库水位涨落速度 v0分别为0.1 m/d、0.5 m/d、1.0 m/d、1.5 m/d、2.5 m/d 和3.5 m/d 时浸润线变化趋势见图4。岸坡断面浸润线呈非稳定变化趋势,即相同时刻t,断面水位变幅随v0的增大而增大,浸润线也更加陡峭;当v0<0.5 m/d 时,浸润线较为缓和,且与库水位保持平行;而当v0=2.5 m/d 时,浸润线滞后于库水位,且水位差将达到5 m 高度。总之,随着库水位涨落速度v0的增大,岸坡浸润线变幅与水力梯度均呈增大趋势。
2.4 降雨入渗对岸坡浸润线的影响
在图1 计算模型中取L=100 m,压力传导系数α=4000 m2/d,有效降雨强度c 分别取0.5 m/d 和0.06 m/d,则降雨量相同的情况下,降雨持续时间为10 d(降雨强度c=0.5 m/d)的连续降雨比50 d(c=0.06 m/d)的连续降雨对岸坡浸润线的影响更为明显,两种情况下的水位差分别为2.21 m 和1.32 m。所以在相同降雨量情况下,岸坡浸润线的变动随有效降雨强度的增大而增大,且越不利于岸坡稳定。

图4 库水位涨落时浸润线变化趋势
2.5 库水位涨落和降雨入渗联合作用对岸坡浸润线的影响
在图1 计算模型中取L=100 m,压力传导系数α=4000 m2/d,库水位涨落速度0.5 m/d,有效降雨强度c 分别取0.1 m/d、0.2 m/d、0.3 m/d、0.5 m/d 和 1 .0 m/d,t=30 d,则根据库水位匀速涨落和降雨入渗联合作用时岸坡浸润线的变动趋势,库水位由145 m 开始上涨,当有效降雨强度c 恰好等于库水位涨速,则浸润线平行于库水位,此时水力梯度趋于零;而当有效降雨强度c 大于库水位涨速,则随x 的增大,岸坡地下水位随之增大,并呈现上凸态势;当有效降雨强度c 小于库水位涨速,则随x的增大,岸坡地下水位反而下降,并呈现下凹态势。库水位由175 m 开始下降时,岸坡浸润线呈陡峭上凸态势。
3 结论
文章从渗流基本原理出发,以非稳定渗流方程及边界条件为依据,进行了库水位匀速涨落和降雨入渗联合作用下浸润线变动规律的计算与分析,并推导出库水位涨落与降雨入渗作用下浸润线的近似解,计算过程中主要以稳定渗流状态下的浸润线作为非稳定渗流情况的初始值,使所求得的浸润线结果更加合理。计算结果同时表明,岸坡浸润线的位置与形状与压力传导系数α 的大小有关,在相同的降雨量情况下,有效降雨强度越大则岸坡浸润线变幅越大,越不利于岸坡稳定。
