弹性轨枕轨道振动特性研究
2019-04-23徐涆文刘晓龙陈秉智肖新标
徐涆文,韩 健,刘晓龙,陈秉智,肖新标
(1.大连交通大学 交通运输工程学院,大连116028;2.西南交通大学 牵引动力国家重点实验室,成都610031)
随着国内列车运行速度的不断提高以及城市轨道交通的迅猛发展,人们对于轨道的减振降噪性能要求越来越高。轮轨滚动噪声一直以来是铁路振动噪声问题的主要来源[1–2],而轨道振动和噪声辐射是轮轨滚动噪声的重要组成部分,因此轨道结构的声振特性分析是铁路减振降噪研究的关键。国外学者对轨道振动研究时间较早,最初只通过简化的梁模型分析钢轨的振动特性。Grassie[3]研究了轨道高频的振动特性,采用Euler 梁和Timoshenko 梁建立单层,双层,三层的轨道离散支撑模型,轨枕,轨垫和道床通过弹簧阻尼单元进行模拟。最后得出的结论是Timoshenko 梁较Euler 梁在相对较高的频域内模拟精度较高。Thompson[4–5]分别建立连续和离散支撑的轨道模型,用Timoshenko 梁模拟钢轨,用两层弹性层模拟轨垫和道床,轨枕通过质量层来模拟,利用复刚度表征弹性层的阻尼特性,最终发现离散的轨下支撑条件能够模拟出钢轨的垂向pinned-pinned振动特性。Grassie[6]进一步分析了考虑弹性轨枕自身弯曲振动影响时轨道的高频振动特性,研究了轨下垫板刚度和轨枕厚度对于轮轨接触力和轨枕应力的影响。结果表明:轨枕的厚度对于轮轨力影响较小,而较薄的轨枕能够降低轨枕弯曲振动时产生的应力。轨垫板刚度对钢轨的动力学性能影响较大,弹性高的轨垫会加大轮轨作用力。为缓解线路的振动传递和噪声影响,减振型轨道结构已经得到广泛运用,弹性轨枕轨道由于其良好的减振降噪性能已经被大量铺设于地铁,隧道等。对于弹性轨枕轨道,国内学者进行了大量的研究。蔡成标等[7]建立车辆-弹性支承块式无砟轨道耦合动力学模型,得出弹性支承块轨道的轨下刚度和枕下刚度的最佳匹配值,以及满足动态轨距扩大限度的结构参数。并研究了不同半径曲线上列车运行安全性与舒适性,以及有砟、无砟轨道过渡段的动力学问题。焦雷[8]通过对车辆、弹性长轨枕轨道以及下部基础进行空间耦合动力学建模,分析弹性长轨枕轨道在直线段和曲线段的动力学优势。通过模态分析、荷载冲击数值模拟和行车过程仿真分析,从频域的角度对弹性长枕轨道结构的减振效果进行分析。最终经过综合考虑得出合理的扣件和枕下橡胶的合理刚度值参数。徐锡江[9]综合考虑弹性轨枕轨道抵抗轮轨横向变形和轨头横移影响的能力,通过仿真得出合理的轨枕埋深尺寸。李丹丹[10]分别对有砟轨道的横向、垂向和无砟轨道的垂向进行谐响应分析,得出各结构的传递函数并分析合理的结构参数。方锐[11–12]通过有限元-边界元的方法分别分析了有砟轨道相关结构参数对于轨道振动和声辐射的影响。姜浩等[13]对弹性长枕、SAT S312 双体轨枕、弹性支承块式轨枕道等3 种减振轨道进行对比分析最后得出弹性长轨枕轨道具有更好的动力学性能的结论。王根平[14]对减振型轨道进行了轨道垂向和纵向振动的传递情况分析,了解到轨下橡胶对于轨道的主要作用频率范围,并利用边界元法对轨道垂向各结构的声辐射进行了对比分析。
目前对于轨道的分析多集中于轨道的动力学性能研究,而对不同弹性轨枕轨道的轨下结构参数对于钢轨振动特性影响的分析较少。钢轨是轨道振动以及声辐射的主要结构,合理选取轨下结构参数能降低钢轨的磨损以及出现波磨的几率,从而优化轮轨之间相互作用[15]。因此详细分析轨枕结构参数的改变对于钢轨的振动特性影响就显得尤为重要。因此本文利用有限元法对两种弹性轨道建立有限元模型并进行谐响应分析,研究轨枕结构参数对钢轨垂向振动特性的影响。对普通短轨枕轨道、弹性短轨枕和弹性长轨枕轨道等3 种轨道建立频域模型,以单位简谐力激励钢轨跨中位置,以普通短轨枕轨道作为初始模型分析不同轨枕结构及其轨下橡胶垫板刚度对钢轨振动特性的影响,为钢轨振动和噪声辐射的研究提供数据基础。
1 非弹性轨枕支撑轨道结构
1.1 轨道计算模型的建立
根据普通轨道的实际尺寸模型和结构参数对其进行有限元建模,相关的结构参数如表1所示。

表1 轨道模型参数
图1为普通轨道的有限元模型。

图1 普通非弹性轨道有限元模型
模型中钢轨、轨枕和道床采用实体单元进行离散,扣件系统采用线性的弹簧阻尼单元进行模拟。由于接触面积较小,本文将作用力作用面积简化为作用点,研究单位垂向简谐力作用下的钢轨垂向振动特性,激励力作用位置为钢轨跨中的钢轨顶面。因为轨道为直线并且激励力为垂向的作用力,因此可按对称问题来处理,取轨道结构的一半进行模拟,这样能够大量减少计算时间[11]。实际中的轨道是一种无限长的结构,魏伟[16]通过对不同长度的轨道进行分析表明,在10 Hz~5 000 Hz 范围内,8 至12 跨的轨道模型已经能够满足各阶共振和反共振特性的计算要求。所以本文采用12 跨的轨道模型对轨道振动特性进行研究。
1.2 模型验证
为了验证计算模型的准确性,本文对某地铁非弹性轨枕轨道进行了力锤敲击试验,获取其频率响应函数,与仿真计算结果进行对比,进而修正有限元模型。试验中,钢轨类型为UIC60,轨枕以及轨道板均为混凝土结构,轨道扣件间距为0.625 m。
图2给出了模拟结果和实际测试结果的加速度导纳对比图。有限元轨道模型中加速度导纳值在频率为230 Hz处和1 020 Hz处出现了2个峰值,第1个峰值对应的是轨道的1阶整体振动模态[9]。第2个振动峰值为钢轨的pinned-pinned振动模态。这和实际的测试结果相吻合,并且频率在大于1 200 Hz 时加速度图像变化趋势和实际结果也是基本吻合的。因此本文建立的模型能够较为准确地反映轨道的振动特性。

图2 钢轨垂向加速度导纳对比
2 弹性支承块轨枕轨道
弹性短轨枕轨道是一种减振型轨道结构,同普通的非弹性轨枕轨道相比,弹性轨枕轨道为了缓解轨道垂向和横向的振动及冲击向下传递,在轨枕下方和轨枕四周加入了弹性橡胶垫和橡胶套结构,实际结构如图3所示。
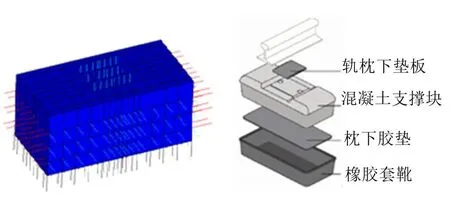
图3 弹性短轨枕结构[13]
为了分析轨枕下的弹性垫板对钢轨振动的影响,在经过上一小节验证的普通轨道模型的基础上,通过弹簧和阻尼单元来模拟实际轨道中的橡胶套和橡胶垫板结构,研究轨枕下加入弹性层后的钢轨振动特性。根据文献[1],轨枕的相关结构参数如下:轨枕弹性模量为3.5×104Mpa,密度为2 500 kg/m3,单块轨枕质量为140 kg,泊松比为0.2。轨枕长×宽×高为700 mm×320 mm×250 mm,扣件刚度同上述普通轨道相同。轨枕下垫板刚度为120×106N/m,轨枕橡胶套为5 000 kN/mm/m2。
图4为弹性短轨枕和普通轨道的加速度导纳对比图,由图可知,当轨枕下方加入橡胶垫板后在频率小于400 Hz的范围内,钢轨激励点垂向加速度导纳曲线出现两个峰值。通过对结构进行模态分析,第一个峰值位置对应钢轨的1 阶垂向弯曲振动模态,轨道结构振型由图5(a)所示。下一个峰值则是由于轨枕相对于钢轨的反相振动引起的,轨道结构振型如图5(b)所示。
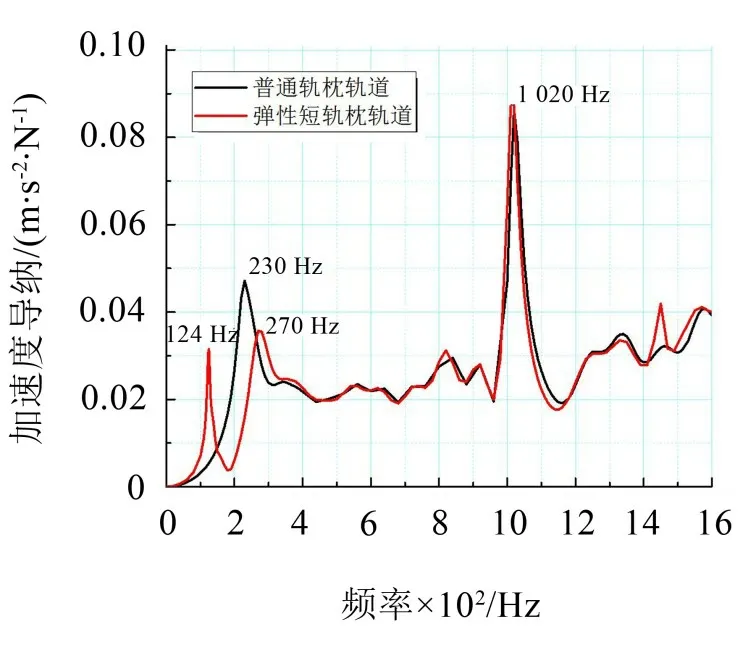
图4 弹性短轨枕钢轨原点处加速度导纳

图5 弹性支承块轨枕轨道钢轨振动模态
2.1 轨枕支撑刚度的影响
研究轨枕下加入弹性层对于钢轨振动的影响,对不同刚度的枕下弹性层进行分析。枕下刚度需要根据实际列车运行情况合理选取,选取轨枕刚度分别为40×106N/m、120×106N/m、200×106N/m 3个工况进行分析。
图6为改变轨枕支撑刚度对钢轨的垂向加速度导纳的影响。
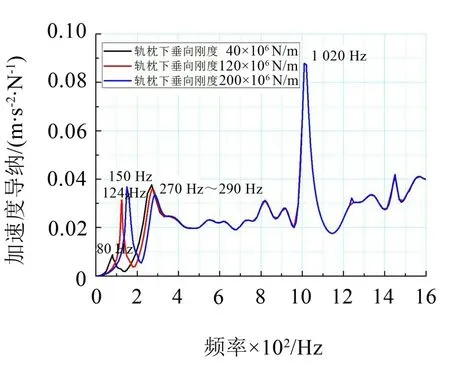
图6 钢轨的原点垂向加速度导纳
由图6 可得,轨枕支撑刚度主要影响400 Hz 以下的钢轨振动。钢轨的1阶弯曲模态和轨枕钢轨反相振动模态频率均随着轨枕垫板的刚度增加向高频移动。而对于低频的2 个振动加速度峰值而言,钢轨1 阶弯曲振动加速度峰值会随着刚度增加而增加。对于轨枕相对于钢轨的反相振动模态,增加轨枕支撑刚度会使轨枕和钢轨的反向振动模态加速度幅值降低。
2.2 弹性轨道轨枕结构参数的影响
目前对弹性轨枕轨道进行钢轨的振动特性分析时多将轨枕简化为质量块模型,忽略了轨枕单纯的尺寸变化对于钢轨垂向振动导纳的影响。因此,本文将分别研究轨枕的质量和尺寸对钢轨垂向振动加速度导纳的影响,明确钢轨振动影响因素,并验证简化建模的合理性。
2.2.1 轨枕质量的影响
对质量为90 kg、140 kg、190 kg 的轨枕进行分析。图8为质量改变对钢轨垂向响应的影响。

图7 轨枕质量改变对于轨道垂向加速度响应的影响
轨枕质量的改变主要影响频率低于400 Hz 的钢轨振动,钢轨的1 阶垂向弯曲模态和钢轨轨枕的反相振动模态所对应的频率均随着轨枕质量的增加而降低。对于钢轨的加速度导纳峰值,钢轨的1 阶弯曲振动加速度幅值随着轨枕质量的增加而降低,而轨枕相对于钢轨的反相振动模态的加速度幅值会随着轨枕质量的增加而增加。
2.2.2 轨枕尺寸的影响
轨枕的初始宽度为320 mm,长度为700 mm。分别调查轨枕长度和轨枕宽度的改变时钢轨垂向振动的情况,分析宽度为270 mm、320 mm、370 mm(长度保持初始尺寸不变)和长度为650 mm、700 mm、750 mm(宽度保持初始尺寸不变)的轨枕对钢轨垂向振动的影响,并且在改变尺寸的同时对轨枕的密度进行调节,从而保证不同尺寸的轨枕具有相同的质量,通过有限元分析得,轨枕尺寸对钢轨振动没有影响,只有质量的改变会对钢轨的低频垂向振动产生较大影响。因此,在研究弹性短轨枕轨道钢轨在1 200 Hz 以下的垂向振动时,可以将轨枕模型简化为质量块,由此验证了简化建模的合理性。
3 弹性长轨枕轨道
弹性长轨枕轨道是在弹性短轨枕的基础上发展起来的新型弹性轨枕轨道。弹性长枕轨道相对于弹性短轨枕主要存在以下技术优点:由于轨枕设计成了长枕,增强了轨枕结构的整体性和轨距保持能力,提高了轨枕稳定性和抗扭转能力。同时也能够较好满足结构的施工和后期维护[13]。根据实际结构建立弹性长轨枕轨道结构的有限元模型如图8所示。

图8 弹性长轨枕结构图[13]
为了保证可对比性,长轨枕的初始数据如下:扣件间距为0.625 m,弹性长轨枕长度为2.5 m,宽度为0.3 m,高度为0.2 m,埋深为140 mm,轨枕胶垫刚度为120×106N/m,轨枕密度为2 500 kg/m3,泊松比为0.2,弹性模量为3.5×1010Pa。对弹性长轨枕模型进行轨枕刚度、轨枕质量和尺寸的参数研究。
图9 为扣件刚度和枕下刚度相同的2 种弹性轨枕轨道的加速度导纳对比图。

图9 弹性长轨枕垂向加速度导纳
由图9可知,针对弹性长轨枕在0~400 Hz范围内出现的3 个峰值,对轨道进行模态分析可得,第1个峰值是由轨道的垂向弯曲振动引起的,结构振型如图10(a)所示。第3个峰值则是由轨枕钢轨的反相振动引起的,如图10(c)所示。而155 Hz的峰值对应的则是钢轨的2 阶垂向弯曲振动和长轨枕的垂向1阶弯曲振动振型,如图10(b)所示。

图10 弹性长轨枕轨道钢轨振动模态
由加速度导纳峰值对比可得,弹性长轨枕轨道在低频激励时产生的垂向加速度较弹性短轨枕轨道更小,因而能够更好地缓解轮轨作用时的振动、冲击。
3.1 轨枕支撑刚度的影响
图11 为弹性长轨枕轨道枕下刚度变化对于钢轨垂向加速度导纳的影响。
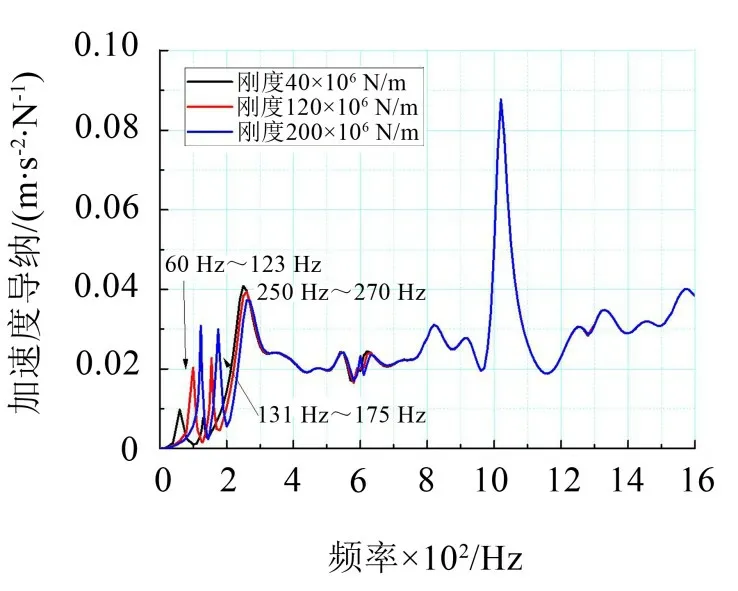
图11 钢轨垂向加速度导纳
由图11可知,改变长轨枕支撑刚度同样主要影响0~400 Hz 的钢轨振动。随着枕下刚度的增加,弹性长轨枕轨道的前3 个振动峰值均向高频移动,钢轨的1阶弯曲模态和长轨枕自身的弯曲振动加速度峰值也随之不断增加,但是轨枕和钢轨的反向振动模态峰值随着轨下刚度的增加而降低,并且相对于钢轨的前2阶振动峰值而言改变幅度较小。因此通过减小弹性长轨枕的轨下刚度能够优化钢轨垂向的振动性能。
3.2 轨枕质量的影响
研究轨枕尺寸相同、质量不同的弹性长轨枕钢轨垂向振动特性。
图12 反映的是随着轨枕质量改变钢轨振动的变化情况,可以看出,在低于钢轨轨枕反相振动频率时,钢轨的2个峰值随轨枕质量的增加而降低,轨枕相对于钢轨的反向振动峰值则随轨枕质量的增加而降低,且峰值的位置均向低频移动。
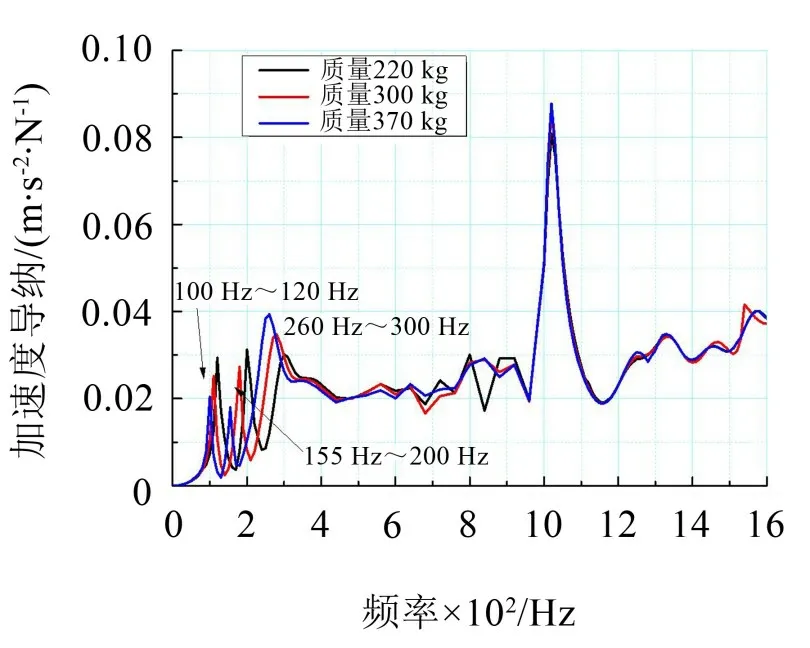
图12 弹性长轨枕轨道质量影响
3.3 轨枕尺寸的影响
同上一小节,在弹性长轨枕轨道轨枕质量相同的情况下改变轨枕尺寸,分析其对钢轨的垂向振动的影响。
图13(a)和图13(b)为长轨枕长度和宽度改变对钢轨垂向振动的影响,可以看出,改变长轨枕的长度和宽度都对155 Hz处的钢轨振动峰值产生影响,钢轨的垂向加速度导纳会随着轨枕长度的增加而降低,轨枕宽度的改变对钢轨垂向振动影响较小。
这是由于弹性长轨枕的第2阶弯曲振动和轨枕的垂向弯曲振动有关,因而长轨枕尺寸的改变主要影响钢轨155 Hz处振动。
对轨枕的质量和尺寸分析表明,弹性长轨枕轨道的钢轨垂向振动与轨枕尺寸、质量是有关的。和弹性短轨枕不同的是,弹性长轨枕钢轨在155 Hz位置的振动对应的是钢轨的2 阶弯曲振动和轨枕的1阶弯曲振动,如果将轨枕简化为刚性质量块模型就会丢失155 Hz 处的钢轨垂向2 阶弯曲振动模态,因此不能将长轨枕简化质量块模型进行模拟。
4 结 语
本文利用有限元法建立2两种弹性支承轨枕轨道模型,分析了在不同轨枕参数下钢轨的振动特性,得出以下结论
(1)在280 Hz(弹性长轨枕轨道)和250 Hz(弹性短轨枕轨道)处出现了由于钢轨和轨枕反相振动引起的钢轨垂向振动峰。弹性长轨枕轨道的一阶弯曲振动频率较弹性短轨枕轨道低,峰值小,由于长轨枕垂向弯曲模态的影响,弹性长轨枕轨道在155 Hz处出现新的振动峰。
(2) 枕下支撑刚度主要对两种弹性轨枕轨道0至400 Hz 的钢轨垂向振动峰产生影响。通过加速度导纳分析可得,降低轨枕下的刚度能够优化钢轨在低频激励下产生的冲击力。
(3) 通过对2 种弹性轨枕轨道的轨枕质量以及尺寸分析后可得,在分析1 200 Hz 以下的弹性短轨枕振动特性时,轨枕可以简化为质量块的形式。
