一种基于等效源法的表面阻抗现场测量方法

李曷冰，胡定玉，刘馨悦，方 宇

（上海工程技术大学 城市轨道交通学院，上海201620）

材料的表面阻抗能够反映材料的声学性质，是材料的重要声学参数之一。在室内噪声控制、户外环境噪声的治理、汽车车内噪声控制等领域具有广泛的应用。准确测量吸声材料的表面阻抗，具有重要的工程意义。

常用的表面阻抗测量方法有传递函数测量法[1]和驻波比法[2–3]，这些方法需要在阻抗管中进行测量，并不能测得材料在现场实际条件下的吸声性能，此外测量时需要将材料切割成特定的小块，通常会对材料造成损伤[4]。采用近场声全息技术进行阻抗测量可以弥补这些不足，Tamura[5–6]使用空间二维傅里叶变换法来测量材料的阻抗，通过采集平行于待测材料表面的两个平行面上的声压值，计算其反射系数，利用反射系数与材料表面阻抗之间的关系间接计算阻抗值，国内聂佳[7]等采用主动声源进行全息计算，对该方法进行了进一步研究；Zhang[8]采用等效源法进行表面阻抗测量，该方法通过采集平行于材料表面上方两条平行线上的声压值，利用基于等效源法的近场声全息技术计算声压和质点振速，直接得到阻抗值。这两种方法不需要将材料切割成特定的小块，但仍需要在消声室环境内进行测量。除此之外，Nava[9]采用边界元法来测量材料的表面阻抗，虽然不需要在消声室环境内进行测量，但要求测量面覆盖整个内空间表面，同时该方法在计算过程中使用了大量的插值运算，导致其计算效率较低。

一般在现场测量环境中，不仅有入射声和反射声，传感器阵列未能覆盖到的区域还会有背侧干扰声。针对这种现场环境，本文提出一种基于等效源法[10]的材料表面阻抗测量方法，通过构造虚拟腔体，来充分考虑测量面各个方向上的声信号，最终对材料表面阻抗进行全息计算。本文以数值仿真的形式，对该测量方法的有效性以及该方法对复杂测量环境的适应能力进行分析验证，最后对主动声源以及等效源的位置等参数进行分析并给出建议。

1 理论基础

1.1 基于等效源法的近场声全息原理

等效源法的原理是[11]布置一系列的简单源（即等效源）来拟合实际声场，通过确定所有等效源的源强实现声场的重建。如图1所示。

图1 等效源法基本原理图

要重建腔体内部的声场，可在腔体外部布置等效源，则腔体内部任一点r处的声压可表示为[12]

式中：i 为虚数单位，ρ0为空气密度，c 为声速，k 为波数，q(r′n)为r′n处的等效源源强，N 表示所布置的等效源个数，g(r,r′n)为自由声场格林函数

当测量面上有M 个测点时，测量面上的声压以矩阵形式表示为

式中：“+”代表求解矩阵的广义逆。

由于重建声场时涉及声波反向传播的问题，因此，在式(1)求解广义逆的过程中，需要采用正则化方法[13]来稳定求解。本文采用的是Tikhonov正则化法，并通过L 曲线法[14]选取正则化参数。利用式(4)进一步求出材料表面的声压和质点振速为

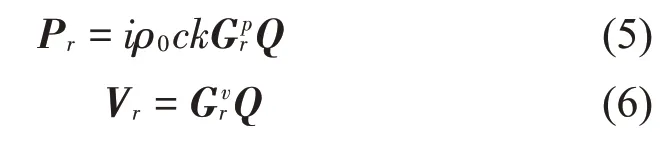
1.2 基于等效源法的表面阻抗测量方法基本原理

本文提出的材料表面阻抗的测量方法原理如图2所示。

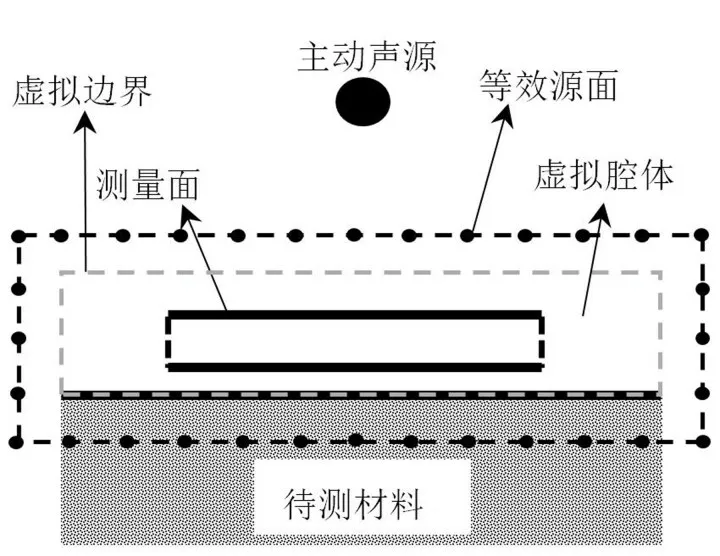
图2 基于等效源法的表面阻抗测量方法基本原理图

首先在材料表面上方布置一个主动声源，然后在主动声源和待测材料中间区域定义一个虚拟腔体，在腔体内部用封闭测量面采集声压。利用基于等效源法的近场声全息技术，计算出虚拟腔体边界处的声压和质点振速。通过式(1)至式(6)求得材料表面任意一点r 处的声压和振速，从而获得表面阻抗为

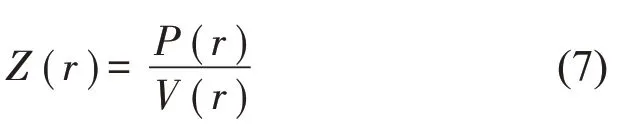
从本文方法原理可以看出，该方法可在现场测量环境下使用，且测量面不需要覆盖整个内空间表面，仅对自己感兴趣的区域进行测量即可。

2 数值仿真

如图3 所示，主动声源置于材料表面上方(0,0,0.3 m)处，干扰声源位于材料表面上方(-0.35 m，0.35 m，0.25 m)处。在等效源面内定义一个封闭的虚拟腔体并在其内部采集声压，测量面由两个距离很近的正方形平面构成，边长均为0.35 m，与待测材料之间的距离分别为0.03 m 和0.01 m，其上共有98个测点，间隔为0.05 m，由于2 个测量面距离很近，因此可以视作是一个封闭的测量面。210 个等效源分布在边长(0.39´0.39´0.16)m3的立方体面上，相邻间隔为0.05 m。仿真时加入信噪比为30 dB 的高斯白噪声。

图3 测量模型示意图

为了定量地评价本文方法，定义计算误差为

式中：Zcal为材料表面上49 个点处的表面阻抗平均值，Ztr为真实的表面阻抗值。

待测材料为纤维状吸声材料,假设材料的厚度为无限大，则其特征阻抗为[15]

式中：σ(流阻率)=50 cgs，Z0=ρ0c 表示空气的特征阻抗。

2.1 方法有效性验证

仿真中分别以单极子和偶极子为主动声源，验证本文方法的有效性。图4(a)和图4(b)分别给出了材料表面阻抗实部与虚部的测量值，可以看出在500 Hz～4 000 Hz 频率范围内，表面阻抗的测量值与理论值吻合较好。

图5给出了采用单极子和偶极子作为主动声源时的测量误差，可看出，在500 Hz～4 000 Hz频率范围内其误差都在10%以内。证明了本文方法对两种不同类型声源的有效性。

2.2 测量环境的适应能力分析

仿真中以偶极子作为主动声源，同时在待测材料上方布置一个偶极子作为干扰声源，其它参数与2.1小节一致。

图4 表面阻抗测量值与理论值的比较

图5 测量误差曲线图

图6给出了本文方法测量值与理论值的比较结果，从图中可看出，在500 Hz～4 000 Hz 频率范围内，本文方法得到的实部和虚部都与理论值吻合较好。图7给出了测量误差曲线，可看出，在500 Hz～4 000 Hz内，误差依然在10%以内，证明了本文方法对复杂测量环境有较好的适应能力。

2.3 主动声源位置分析

保持2.2小节中的仿真设置不变，改变主动声源位置(如图3 所示)z0，来分析其对测量误差的影响。图8给出了500 Hz、1 000 Hz和2 000 Hz频率下不同位置处的测量误差。可看出，在0.2 m～0.4 m 范围内误差最小。因此，建议将主动声源放置于材料表面上方0.2 m～0.4 m处。

2.4 等效源位置分析

保持2.2小节中的仿真设置不变，改变等效源面上下表面的位置(如图3所示)z1和z2，来分析其对阻抗测误差的影响。图9 给出了500 Hz、1 000 Hz 和2 000 Hz 3个频率的分析结果。

可看出，当等效源面上下表面距材料表面0.075 m～0.175 m 时测量误差最小。因此，建议等效源面上下表面到材料表面距离为0.075 m～0.175 m，且关于材料表面对称。

图6 存在干扰条件下表面阻抗测量值

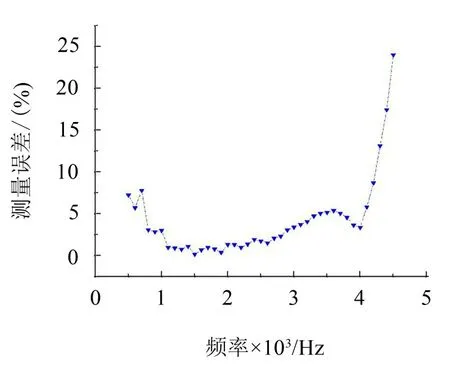
图7 存在干扰条件下表面阻抗测量误差曲线图

图8 声源位置对精度的影响

3 结语

本文提出了一种基于等效源法的材料表面阻抗测量方法，通过引入虚拟腔体，将问题转换成近场声全息的内部问题，实现了复杂环境下对材料表面阻抗的测量，且该方法只需要对感兴趣的部分单独测量。分别采用单极子和偶极子声源模型作为主动声源，并在测量环境中加入干扰声源进行数值仿真，结果表明，在500 Hz～4 000 Hz内，本文方法能准确获取表面阻抗，且对测量环境具有良好的适应能力。通过分析主动声源以及等效源位置对测量误差的影响，得出主动声源的最优位置为材料表面上方0.2 m～0.4 m处；等效源面上下表面最优位置为距材料表面0.075 m～0.175 m处，且关于材料表面对称。

图9 测量误差随等效源位置的变化图