基于字典训练的Bregman迭代地震数据重建
2019-04-23
(东北石油大学 计算机与信息技术学院, 大庆 163000)
0 引言
目前,随着国内外油气勘探技术的不断进步,地质勘探技术逐渐难以满足现在的地质勘探的需求。在石油工业日渐成熟的过程中,勘探的难度也不断增大,探测地区的客观环境变得日益复杂,在各种因素的影响情况下,将导致地震数据不规则、不完整,使得勘探得到的地震数据的道缺失现象相对增多,这些问题对地震数据的后续处理与解释造成不利影响,给油气藏位置的判断增加难度。传统的地震数据重建方法为奈奎斯特Nyqusit采样定理它要求采样频率一定要在信号带宽的2倍以上,而这种方法使勘探成本的增加。为了解决这个问题,需要寻找更加适合地震数据的重建算法,对地震数据进行规则重建,得到精度较高、更加完整的地震数据,以降低地震勘探过程的成本。然而随着信号重建技术的日益进步,Donoho、Emmanuel Candès与Terence Tao等人提出压缩感知理论,该理论为信号处理提供了全新的研究方向。压缩感知理论一般分为稀疏变换、构造采样矩阵与信号重建3个部分,研究领域对稀疏表示和重建算法颇为重视,在稀疏表示研究中Mallat、Zhang二人构造了一种新的稀疏分解,将压缩感知理论框架与冗余字典相结合,取得了进一步的发展。随后Aharon等人将K-means聚类算法改进为K-SVD算法,但这类方法要求相对较多的计算量与较大的存储空间。为了完善现有的重建算法和压缩感知理论框架,还需要对冗余字典类方法进行更多的研究。在重建算法研究方面,Tropp和Gilbert提出的正交匹配追踪算法[1]不仅提高迭代收敛的速度,且能得到较好的重建效果;BP算法为求得全局最优解会进行穷举运算,重建精度和稳定性好,能够解决夹带的假频问题,但本身算法的复杂度导致计算时间过长。对此在国内也开展了一些研究,如哈尔滨工业大学的张键,赵德斌提出了一种基于分离 Bregman 迭代方法求解协同稀疏模型正则化的图像压缩感知重建算法,能够在有效地刻画图像的局部平滑性和非局部自相似性的同时,获得更高质量的重建效果[2]。总体来说,国内在压缩感知的研究方面还需要继续进行,大多是基于各种理论的应用。目前仍需开发低复杂度、高压缩率、高重建度的实用算法。
为了解决由地震数据的道缺失所导致的问题,就需要对地震数据重建进行深入的研究。本文根据压缩感知理论,将K-SVD分解算法与Bregman迭代相结合,对地震数据进行仿真模拟试验,进行地震数据的重建,得到完整地震数据。
1 基于K-SVD字典训练的Bregman迭代地震数据重建
1.1 Bregman 迭代方法
在图像处理领域与压缩感知理论框架中,选用适合重建过程的Bregman迭代算法,能使用稀疏信号更好地匹配原地震数据奠定基础。起初是Osher等人将Bregman散度的概念引入到迭代正则化过程中,实现了满足平滑去噪需求的Bregman迭代。随后Cai等人在研究基追踪重建时,提出将不动点迭代法[3]与Bregman迭代算法[4]相结合,提出了线性Bregman迭代算法,虽然线性Bregman迭代算法可以对传统的BP问题进行求解,但是在信号分析、图像处理等领域中,一般是针对l1范数最小化求解为式(1)。
(1)
为了解决上述形式的l1范数最小化求解问题,Tom Glodstein等[3]结合Bregman迭代方法和算子分裂技术,于2008年提出了分裂Bregman迭代(Split-Bregman iteration, SBI)算法。分裂Bregman迭代算法的收敛速度更快,有着易于编程实现、易并行化等优点。式(1)根据凸优化理论可得而式(2)是无约束问题最优化,为式(2)。
(2)
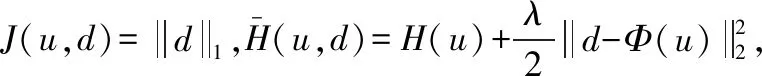
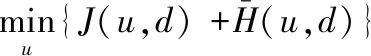
(3)
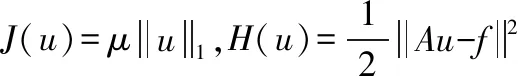
u0←0,p0←0;
Fork=0,1,… do
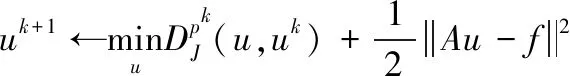
(4)
fk+1←f+(fk-Auk)
(5)
利用式(4)和(5)对该问题进行求解,可得到分裂Bregman迭代形式,即式(6)。
bk+1=bk+(Φ(uk)-dk)
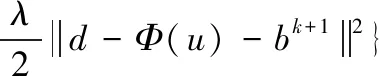
(6)
由文献[5]可知,分裂Bregman迭代算法的收敛速度更快,有着易于编程实现、易并行化等优点。因此本文选择分裂Bregman迭代算法来进行地震数据的重建。
2.2 K-SVD字典训练
在2006年Michal Aharon等人[6]基于K-means算法,提出了K-SVD字典训练算法,在国内唐刚、周亚同等已在地震数据重建上使用了K-SVD算法。本文提出的地震数据算法的插值循环中包含了K-SVD算法,它在整个稀疏变换中,不停的更新超完备字典中的列,在结束迭代时就得到了能更好的对图像进行描述的超完备字典。其另一个优点就是能够与所有的分解算法结合,通过对超完备字典的更新,提高变换后图像的稀疏性,加快了分解和收敛的速度。基于K-SVD的超完备字典训练算法具体流程描述如式(7)。
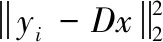
(7)
先利用式(2-7),通过超完备字典D的迭代训练,如果有D的第k列向量为dk,则此时可以将式(7)转化为式(8)。
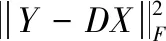
(8)
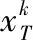

(9)
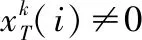
(10)
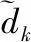
1.3 地震数据重建的实现
本文在Bregman迭代重建算法框架中,使用K-SVD对联合数据样本进行初步的数据处理,每次迭代最后进行插值处理,进行多次迭代后得出重建的地震数据,实验说明,使用本文算法能够更有效的进行地震数据的重建。具体实施步骤如下。
(1)字典初始化。本文使用处理过的地震数据作为联合数据样本,生成初始字典。
(2)稀疏变换。利用已知字典D,根据OMP算法和式(7),求解每一个样本yi的稀疏系数向量xi。
(3)字典更新。固定向量xi后更新字典D,对字典D的每一列向量(dk,k=1,2,3…)进行更新,此时的具体分解形式可以用式(8)与(10)来表达。即式(11)。
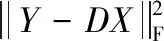
(11)
利用上述方法更新D的每一列和稀疏编码,当迭代次数达到上限或者残差足够小的时候,得出新的字典。否则继续迭代步骤(2)。
(5)对得到的结果进行插值处理,如果未满足迭代次数,则返回步骤(5)继续迭代,若满足迭代次数,则退出迭代过程并输出地震数据重建结果。
2 地震数据重建实验及分析
本文使用的地震数据如图1所示。

(a) 地震数据 A(b) 地震数据 B
图1 完整地震数据
为两幅地震数据单炮记录,总共128道数据,横向为地震道轴,纵向为时间轴,长度为512。
对地震数据A和地震数据B进行40%随机道缺失采样(即采样率为60%)后,地震数据如图2所示:

(a) 随机道缺失的地震数据A(PSNR=20.789 4)(b) 随机道缺失的地震数据B (PSNR=20.544 6)
图2 采样后的地震数据(采样率为60%)
根据上节所叙述的原理及步骤,对地震数据A和地震数据B进行重建的地震数据重建方法进结果分析,如图3所示。

(a) 重建后的地震数据A(PSNR=26.431 4)(b) 重建后的地震数据B(PSNR=25.311 6)

图3 本文算法重建后的地震数据
4 总结
经对Bregman迭代算法分析后,提出了改进型的基于K-SVD的分裂Bregman迭代算法,在分裂Bregman迭代框架中,采用K-SVD算法进行自适应字典训练,进一步提高了地震数据重建的准确性。结合K-SVD的分裂Bregman迭代重建算法在重建地震数据的结果中,相对于道缺失的采样地震数据,观察其重建结果,发现两张图像PSNR的提升都在5左右通过实验,通过实验说明本文算法能够更好的重建图像的纹理,更精确的还原地震数据的原貌。
