基于换电运营模式的电动车电池充电策略研究

， ， ，

(同济大学 电子与信息工程学院,上海 201804)

0 引言

随着能源短缺日益严重，环保呼声高涨，电动汽车(electric vehicle, EV)作为一种低碳、情节的交通工具，受到世界各国政府的高度关注[1]，成为我国新时期重点发展的7个战略性新兴产业之一[2]。电池是电动汽车运行的能量来源。规模化电动汽车运行以后，必将带来蓄电池的充电问题[3]。本文通过蒙特卡洛方法模拟出电动汽车的出行分布特征和换电需求分布特征，并由此使用线性规划算法求解运营成本最低的充电方案。

换电模式是一种基于换电站(Battery Swap Station, BSS)的充电模式，换电技术最初是由Renault和Better Place公司提出的，目前成为电动汽车产业发展的新模式。在这种模式下，用户只需要在一个距离最近的换电站或配送站，用他们需要充电的电池换取已充满的电池即可。由于换电式电动汽车在出行距离和能源交换方式方面的优势，基于换电模式的充电策略已经提出，并且在近几年受到了越来越多的关注[4]。

本文利用真实的私家车出行数据，通过蒙特卡洛方法模拟出大规模电动汽车在一天内的出行分布和换电需求分布，再基于这些模型建立了换电站的运营成本模型，包括了电池充电成本、储备电池成本和充换电设备成本。在此基础上，利用线性规划算法求出最优的电池充电调度策略。

1 基于蒙特卡洛方法的电动汽车换电需求分析

蒙特卡洛方法[5]的基本思想是当所求解的问题是某种随机时间出现的概率，或者是某个随机变量的期望值时，通过某种“随机试验”的方法，以这种事件出现的频率估计这一随机事件的概率，或者得到这个变量的某些数字特征，并将其作为问题的解。由于电动汽车的换电服务仍是一个正在规划的行业，目前没有确切的换电服务需求模型，因此，本文查阅了小汽车出行分布模型，通过蒙特卡洛方法模拟每辆电动汽车在一个统计周期内的出行分布和剩余电量分布，从而得到电动汽车换电服务需求模型。

文献[6]统计了北京市居民小汽车的出行时间分布，通过统计可以发现，小汽车的日均出行次数为3.16次/日。考虑到每天的差异性，对于N辆电动汽车，可以假设每天出行的总数量服从U[3N,3.32N]的均匀分布。本文依据北京市居民小汽车的出行时间分布和出行比例作为电动汽车的出行比例，在一小时内按照均匀分布,如图1所示。

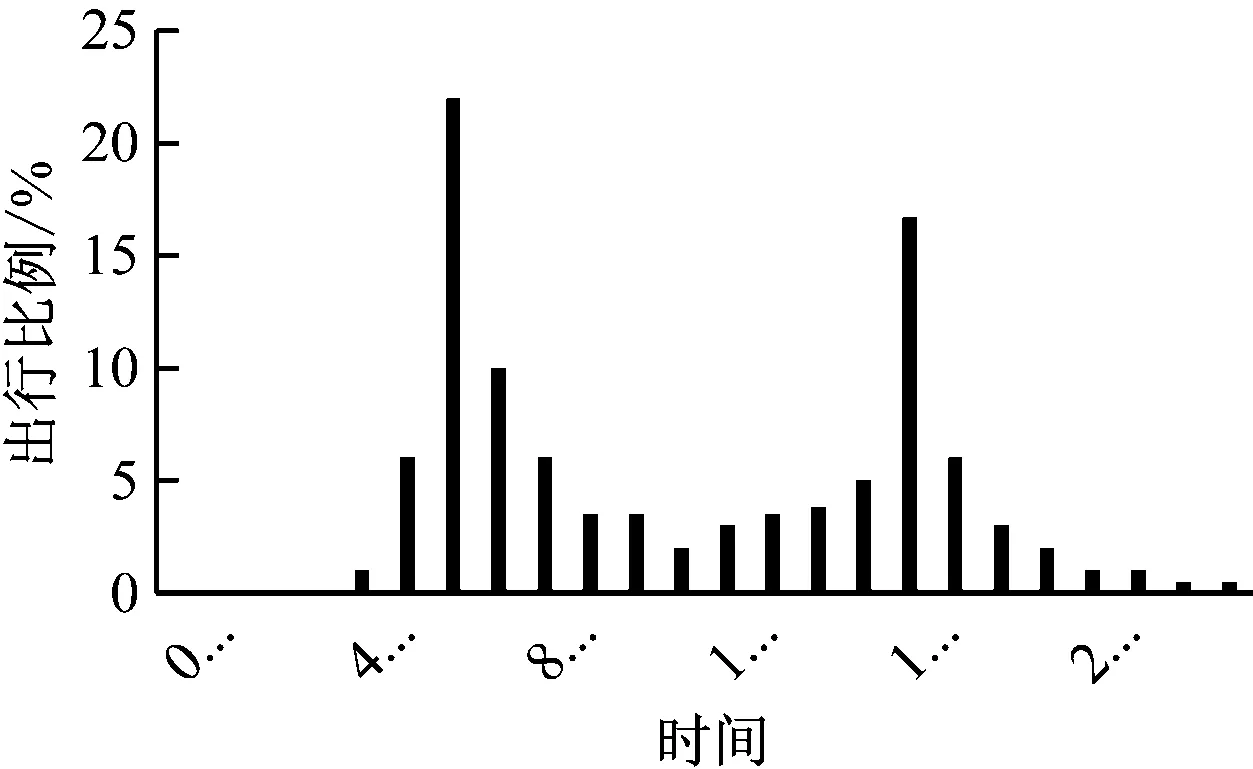
图1 私家车出行比例

文献[7]按照不同的城市规模和城市布局建立了私家车出行距离分布模型，发现城市私家车每次出行的距离服从瑞利(Rayleigh)分布，并且由于城市规模与布局的不同，瑞利分布的参数λ也不同，对于上海这种大型城市而言，可选λ=11.17。

假设电池容量为19.2 kWh，从满电到空电行驶100 km。电动汽车的行驶行为是其主要的耗电原因，因此若要建立电动汽车换电的日需求模型，必须描述车辆在一天内的行驶状况。考虑到车速不断变化会对行驶距离造成影响，进而影响到电池电量消耗的过程，可假设电动汽车在行驶过程中每个时刻的时速S满足正态分布，本章的每个时刻表示1分钟的时长，可认为车辆速度在1分钟内是恒定的。S服从N[21,32]的正态分布。

本文以换电阈值作为判断电动汽车是否前往换电站进行换电服务的依据，换电阈值分为两类：一类是车辆在剩余电量过低时，为了维持车辆良好的使用状态所产生的换电需求，以QL表示其换电阈值，称为低电量阈值，该类型需求为低电量换电需求；另一类时电动汽车在一天最后一次出行结束后，为次日进行电能储备而产生换电需求，以QS表示其换电阈值，称为储备阈值，该类型需求为储备换电需求。依据QS的定义，可以认为QL小于等于QS，并且认为电动汽车在计算初始时刻的电量与储备阈值有关。假设QS=[0.35,0.55],QL=[0.10,0.20]]，电动汽车在日常行驶中，会在电量位于QS范围内时随机前往换电站进行换电，当电动汽车在进行一天内的最后一次行驶活动时，若结束时的电量位于QL范围内，则电动汽车有可能在最后一次行驶的全过程内接受一次换电服务，进行换电服务的时间满足均匀分布。

上海市目前常住人口为2 415万，其中嘉定区常住人口为143万人，至2017年上海市私家车保有量为213万辆，取电动汽车渗透率为5%，可算出嘉定区电动汽车数量为6 330辆，本文将这6 330辆电动汽车作为换电服务的研究对象。

考虑到车辆的运行规律，部分车辆的运行可能会持续到24:00之后，且车辆每天第一次出行时的电池电量不一定满足均匀分布。为了减小对分析结果的影响，所有计算均以2:00作为开始的时刻，连续进行两天的计算，并将第二天的结果作为最终的模拟结果。通过蒙特卡洛方法得到的电动汽车换电的时间分布模型,如图2所示。

图2 电动汽车的日换电需求分布

经过一天的运行，6 330辆电动汽车会产生2 353次换电需求，如何对这些换电需求进行优化，从而减少换电站的运营成本是本文研究的核心。

2 电动汽车换电站的运营成本分析

电动汽车换电的成本模型可以分为3部分，电池充电成本，储备电池成本和充换电设备成本。

(1) 电池充电成本

在此使用两部制电价进行充电成本模型的建立，充电成本分为电量电价成本和基本电价成本，分别与实际充电电量与最大充电功率相关，电价使用上海市商业分时电价，具体参数如表1所示。

表1 分时电价与最大需求参数

充电成本的公式为式(1)。

(1)

式中:

Ccharge表示充电成本；

∑t∈T(C(t)×E(t)×P)表示电量电价；

C(t)表示在t时刻充电的电池数量；

E(t)表示t时刻的电价，P表示电池充电功率；

kmax_demand表示最大需量参数。

(2) 储备电池成本

采用换电模式进行能量更换，电动汽车更换下的电池由集中式充电站安排充电，待充满后电池会在下一个时刻运至电池配送站等待电动汽车取用，并在为电动汽车更换电池时获得其他待充电电池。电池循环示意图如图3所示。

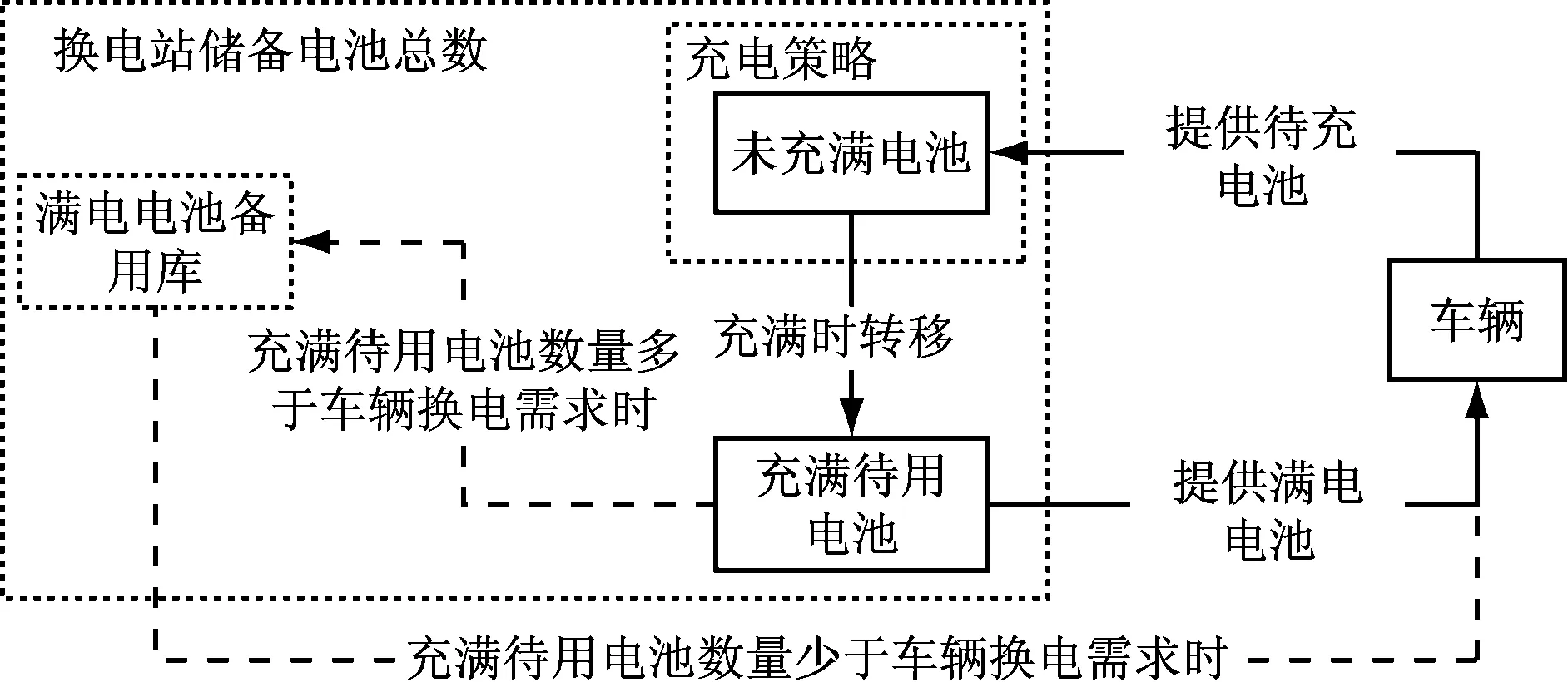
图3 电池循环示意图

将模型中充电站所保有的电池都视作站内储备库电池，根据电池循环流程图可知，储备库电池分为满电待用电池、正在充电电池和待充电电池，分别用两个集合BF,BC和BN分别表示，可知换电站的储备电池总数为|BT|=|BF|+|BC|+|BN|。

对于时刻t而言，对于BN,BC和BF而言分别存在约束条件，如式(2)。

(2)

式中:

BF(t),BC(t),BN(t)分别表示t时刻满电待用电池、正在充电电池和待充电电池的数量；

SW(t)表示t时刻更换下的待充电池数量；

CS(t)表示t时刻开始充电的电池数量，只要满足上述约束条件即为储备电池的可行解，储备电池成本正比于最少储备电池的数量；

CE(t)表示t时刻结束充电的电池数量。

储备电池成本的计算式为式(3)。

Cbattery=|BT|×kbattery

(3)

式中，kbattery为折算后每块电池每日的折旧成本。

(3) 充电设备成本

充电设备成本为换电站为充电准备的电池充电机的成本，该成本正比与充电策略中的最大同时充电电池数。其计算式为式(4)。

(4)

式中，kche为折算后的单台充电设备每日运营成本。

3 换电站内电池充电策略的优化方法分析

换电站对电池充电策略相关的运营成本主要包括了电池充电成本，储备电池成本和充电设备成本。

假设充电机的功率为5 kW，电池功率为19.2 kWh，充电策略将一天划分为每段4小时的6个时段，分别2:00-6:00, 6:00-10:00,10:00-14:00,14:00-18:00,18:00-22:00,22:00-次日2:00。在每个时段开始时将电池统一接入充电装置，在每个时段结束时将已充满的电池统一从充电装置中移除，故每个时段的充电电池数量即为该时段开始时进行充电的电池数量，每个时段获得的新充满待用电池数量为上一时段开始充电的电池数量，如式(5)。

(5)

6个时间段的电价向量e=[0.291 0,0.291 0,1.005 5,1.005 5,0.892 3,1.118 8]kWh。通过换电模型可知一天内更换的电池总量为2 353块，平均每块电池需要充电12.33 kWh。假设充电策略为c=[c1,c2,c3,c4,c5,c6]，则电量电价成本为e×c，基本电价为40.5/30×5×max(c)，充电设备运营成本为0.72×max(c)。

可以看出，构建的运营成本模型主要存在两个非线性因素：充电设备成本计算过程中的电池最大充电数量max(c)和储备电池成本的迭代计算过程。在使用算法对系统进行优化前，需要首先消除这两项非线性因素。

对于非线性变量max(c)，通过对充电成本的定性研究可以发现，充电最多的时刻一定位于电价最低的时刻，即max(c)=max(c1,c2)，由于c1和c2为换电服务的低谷时间段，在这段时间内充满电池的数量高于换电服务需求的电池数量，故c1和c2的选择只影响充电设备成本，而不会影响充电成本和储备电池成本。因此，最优的充电策略会让c1和c2的值相等，且为向量c=[c1,c2,c3,c4,c5,c6]的最大元素，故可令c1=c2,max(c)=c1。

对于储备电池成本而言，消除非线性因素的方法是假设[bf,bc,bn]为一天开始时换电供应商拥有的满电待用电池、正在充电电池和待充电电池数量。将[bf,bc,bn]作为待求变量放入充电规划模型中，即将规划的解由c=[c1,c2,c3,c4,c5,c6]扩充为c=[c1,c2,c3,c4,c5,c6,bf,bc,bn]。

此时还需对式(2)的约束做线性化操作。

对BC和BT的线性化操作类似于BF，在此不做过多描述。

因此，充电策略的规划模型为式(6)。

式中，

(6)

4 算例分析

配送站和换电站中的储备电池，充电设备和换电设备具有不同的使用成本和使用寿命。对各类资源的单价及维护费用按表2进行设置。

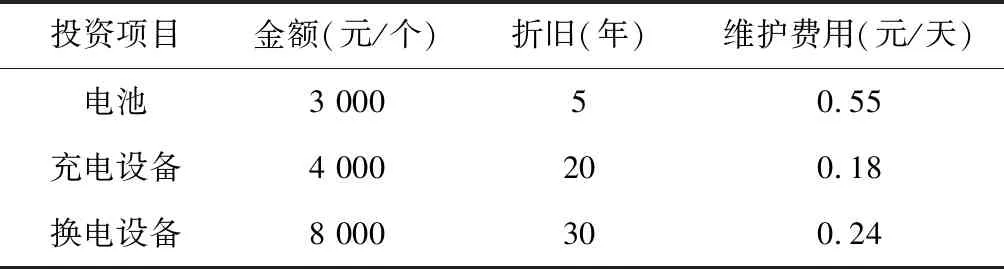
表2 设备单价及维护费参数

4.1 未进行充电策略优化的成本分析

通过蒙特卡洛方法模拟出的换电分布模型(图2)作为研究对象，在没有任何优化策略的条件下，可计算电动汽车换电服务商每天的运营成本。

a) 充电成本

由于电池总电量为19.2 kWh，假设充电功率为5 kW，则认为单块电池的充电周期为4小时，因此可将一天分成6个充电周期，每个周期内充电站将上个充电周期内更换下的待充电池充满，并将已充满的电池配送至配送站。充电站在6个充电周期内充的电池数量,如图4所示。

在这样的充电分布下，充电站每日的电量电价成本为27 682元/天，折算的基础电价为7 924元。

b) 储备电池成本

储备电池的数量与充电分布和换电分布均相关，在没有任何优化措施的条件下，每个充电周期会将上个周期更换的待充电池充满，并将这些电池在下个充电周期开始时配送至各配送站。通过24小时的迭代计算可求出储备电池数量为1 859块，各个充电周期内的已充满电池和未充满电池如图5所示。由表2得kbattery=2.19，可计算出储备电池成本为4 071元。

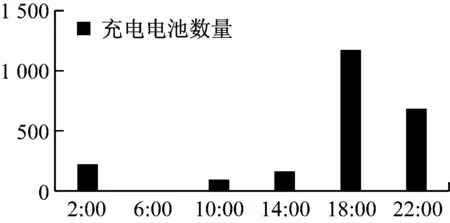
图4 即换即充策略下的充电电池分布

c) 充电设备成本

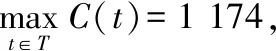
综上所述，在没有任何优化策略时，换电站每日运营总成本为40 522元。如图5所示。

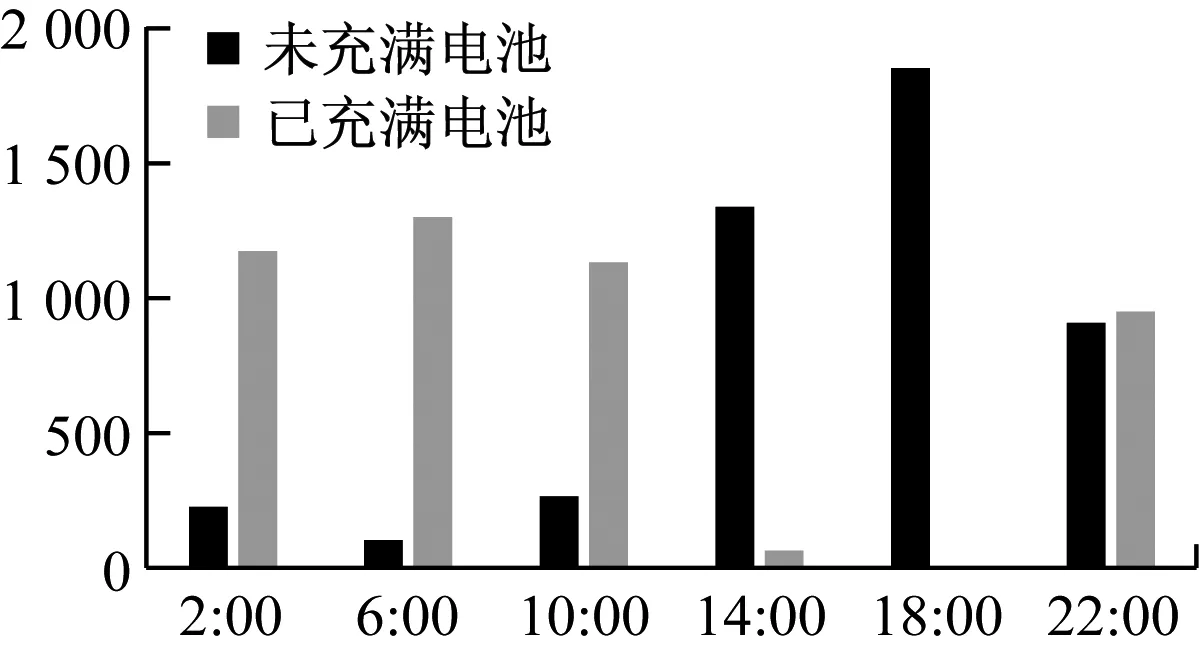
图5 充电站已充满电池与未充满电池分布

4.2 进行充电策略优化的成本分析

对以上模型进行线性规划，可求得最优解为c=[1 177,0,0,0,0,1 176]，可以看出此时充电策略(如图6)会偏向电价较低的时间段进行充电。此时的储备电池数量为2 348块，换电站内3种类型的电池分布如图6所示。

图6 优化充电策略后充电站充电策略

使用优化充电策略后，可得换电商各部分成本为：

电量电价成本：8 448元;

基本电价成本：7 938元;

充电设备成本：847元;

储备电池成本：5 142元。

综上，使用充电策略优化后，换电商和充电相关的运营总成本为24 175元。使用充电策略优化后的各项运营成本与未进行充电策略优化前的各项运营成本对比如表3所示。

由表3可得，在建立的换电服务商的运营成本模型中，相比即换即充的充电策略，使用优化后的充电策略能通过减少充电成本和储备电池的成本，减少约40%的运营成本。如图7所示。

表3 充电策略优化前后的换电站运营成本分析

图7 优化充电策略后充电站各类电池分布情况

5 总结

本文主要通过蒙特卡洛方法模拟出换电式电动汽车在一天内的出行分布特征和换电需求分布特征，并建立了换电运营商的运营成本模型。同时，本文建立了换电运营成本与电池充电策略之间的关系模型，并将其规约为一个线性规划求解最优值的问题。最后，本文使用了整数线性规划算法对充电策略进行求解，并与未进行优化前的成本进行比较和分析。可以看出，在使用的算例中，用充电策略优化后，换电运营商的成本相比未使用充电策略优化前减少了约40%。