基于模糊层次分析法的射击有利度分析模型

李彩峰，徐 锋，张玉梅，孟丽洁，王 伟

（北方自动控制技术研究所，太原 030006）

0 引言

射击有利度是评估武器火力打击效果的一种指标，它的计算是火力分配中重要的一环，防空火炮的射击有利度是指其对空袭兵器施行打击的有利水平，结合对来袭兵器的威胁度评估和射击有利度，可以有效地分配防空火力单元。对射击有利度有影响的内容具有多因素、多层次的特点，因此，适合构建多层次结构模型。再使用层次分析法的理论就可以分析出各个因素的权重，然后再结合火炮和空袭兵器的具体参数即可计算出射击有利度。

层次分析法中所有的计算都依赖于其比较判断矩阵的构建，而采用传统理论构建的比较判断矩阵存在如下缺陷：1）采用数值1～9表示相对重要的程度，同时采用其倒数表示相对不重要的程度，这种表示方法不具备线性性。2）比较判断矩阵的一致性需要计算矩阵的最大特征值，计算复杂度相对较高。3）判别矩阵的一致性验证CR＜0.1缺乏理论依据。4）一致性的验证与人类的思维差异性较大。5）判断矩阵在出现不一致的情况下时再调整较为复杂。针对这些问题，按照比较重要程度的线性关系，再结合人类思维的一致性，从而提出模糊一致矩阵，构建模糊层次分析法。本文利用文献[1]中构建的防空火炮的射击有利度模型比较了两种方法。

1 模糊层次分析法

1.1 层次分析法

层次分析法（Analytic Hierarchy Process，AHP）是一种将定性分析转化为定量分析的有效方法。层次分析法的实现一般需要以下4个步骤。

1.1.1 建立模型

建多层次模型是层次分析法的基础。如图1所示，多层次模型由最上层的目标层、制约目标层的准则层和对准则层直接相关的方案层[2]。

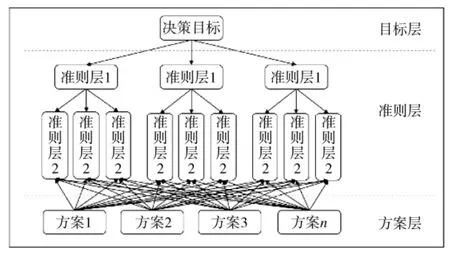
图1 多层次模型结构

构建准则层是为了细分影响决策目标的因素，这些影响因素具有独立性，根据需要可将准则层再分解，构建树状的多层次模型，如图1所示，模型中的每一个叶子节点都与备选方案直接相关。

1.1.2 生成比较判断矩阵

建立比较判断矩阵是建模过程中由定性转为定量的关键一步，一般情况下使用表1表示两个因素之间的相对重要程度。

相对应地，使用这些数字的倒数表示相对不重要的程度。通过一定的调查方法，比如专家咨询法，得出各个准则之间的重要关系数值，生成比较判断矩阵，该矩阵中第i行第j列的元素表示第i个元素相比于第j个元素的重要程度，一般而言，该矩阵对角线对称的元素互为倒数[3-4]。

1.1.3 一致性检验

在实际情况下，比较判断矩阵中元素的选取可能不符合实际情况，比如元素1相对于元素2重要程度为9，元素2相对于元素3重要程度为3，但是元素1相对于元素3的重要程度为2，就不符合一致性规则。因此，一个为经过一致性检验的比较判断矩阵是无法使用的。层次分析法采用如下步骤进行检验：1）计算一致性指标，其中n表示元素的个数，即比较判断矩阵的阶数，表示比较判断矩阵的最大特征值。2）查询一致性指标RI，如表2所示。

1.1.4 结果计算

根据比较判断矩阵可以得到各个因素的权重，计算方法有几何平均法、算数平均法、最小二乘法和特征向量法等。然后给出各个方案在不同的叶子节点上归一化后的值，将归一化后的值与权重相乘后相加直到求出决策目标的值，即根据决策目标值的大小比较各个方案的优劣[5-6]。

1.2 模糊一致矩阵

针对引言中提到的层次分析法中比较判断矩阵存在的问题，采用模糊一致矩阵代替传统层次分析法中的比较判断模型，可以较好地解决这些问题。

1.2.1 定义

设存在阶数为n的方阵Cn×n，其第i行第j列的元素为cij，满足以下3个条件：

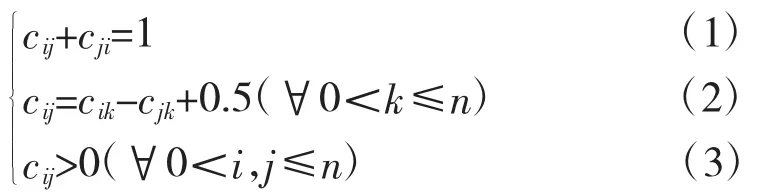
则称方阵C为模糊一致矩阵，如果方阵不满足条件2，则称其为模糊矩阵。

1.2.2 特性

模糊一致矩阵具备模糊性、对称性和一致性：

1）模糊性，鉴于需要得出各种因素之间的权重，故而将两种元素之间的关系定义为模糊关系“XX比XX重要”，所以可以使用0到1之间的数值衡量这种关系，如果使用其他数值，就可以使用归一化方法将其放缩到0到1之间。

2）对称性，关系“两者同样重要”可以选取0到1之间的中间值0.5来表示，大于0.5的值表示前者比后者重要，相应地，小于0.5的值表示后者比前者重要，假设元素1比元素2的重要关系的数值为m，那么根据上述取值的方式可知1-m则表示元素1不比元素2重要的程度，即元素2比元素1重要的程度。这即模糊一致矩阵的对称性。

3）一致性，使用数值A表示元素1比元素2重要的程度，B表示元素2比元素3重要的程度，C表示元素1比元素3重要的程度，根据人类思维的一致性，C-B表示元素1相对于元素2的相对重要程度，再加上元素2相对于本身的重要程度即元素1比元素2的重要程度，即A=C-B+0.5。

模糊性从模糊关系的角度给出了元素之间重要程度的关系，对称性从线性角度给出了衡量比较元素之间重要程度的数量值，一致性不仅是从逻辑上给出了其定义，而且其检验相对于计算最大特征值的方式计算复杂度低。

进一步对模型概率估计结果进行了研究,以对比UIF-IMM 2与UIF-IMM 1两种方法,找出提高位置和角度精度的原因.如图5所示,UIF-IMM 2考虑了基于各种传感器的累积似然函数,使滤波器能够更精确地估计模型概率,从而对状态和协方差进行更精确的融合和估计.

类似于比较判断矩阵，可以给出模糊一致矩阵的度量及其含义，如表3所示。

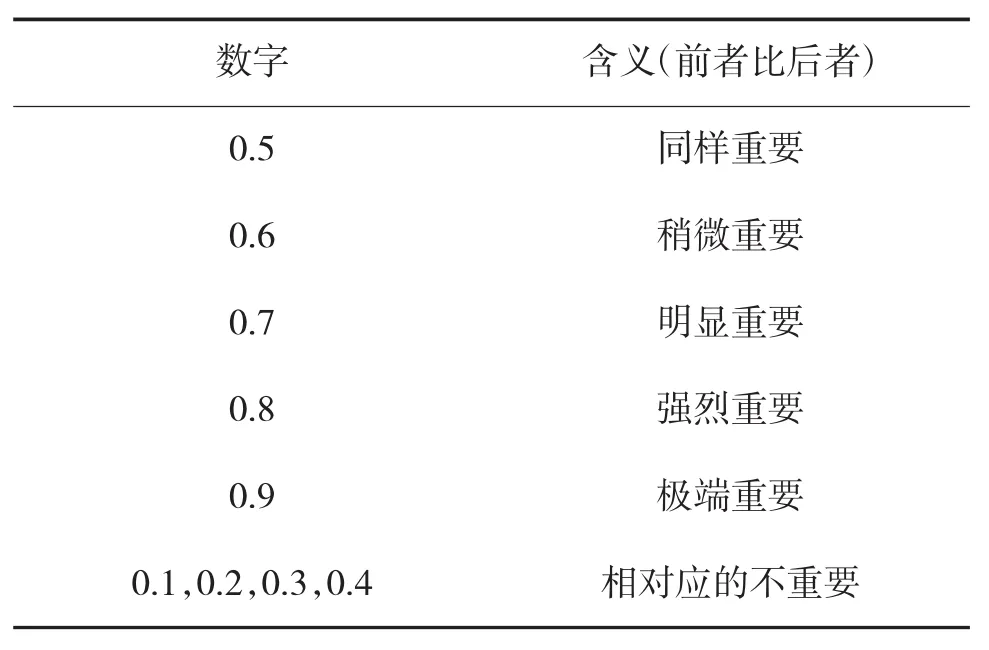
表3 模糊一致矩阵的度量及其含义

2 实例

文献[1]构建了一种基于层次分析法的防空火炮的射击有利度模型，本节将使用模糊层次分析法重新构建该模型，并比较两者之间的差异。

2.1 模型

利用层次分析法构建如图2所示的防空火炮对不同批次的空袭目标的射击有利度层次结构模型：

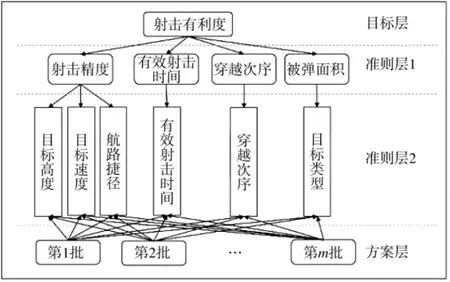
图2 射击有利度的多层次模型

射击精度越高、有效射击时间越长、穿越次序越早、目标被弹面积越大，对射击越有利。而针对射击精度而言，目标高度越低、目标速度越低，射击精度越高，目标航路捷径等于瞄准死界半径时，射击精度最大，大于瞄准死界时，航路捷径越大，精度越低，小于瞄准死界时，无法瞄准故而精度为0。针对目标被弹面积而言，可以根据不同类型的目标判断其被弹面积[7-8]。

空袭武器的飞行高度、飞行速度、航路捷径、飞行时间、机型大小、穿越次序一般无法直接用于模型，需要使用效用方法将这些数据归一化后带入模型，效用方法参见文献[1]。

2.2 数据计算

2.2.1 比较判断矩阵与模糊一致矩阵

使用归一化方法可以直接将比较判断矩阵转化为模糊矩阵，然后对模糊矩阵进行修正可以得到模糊一致矩阵。由文献[1]中层次分析法得到的比较判断矩阵如表4、表5所示。

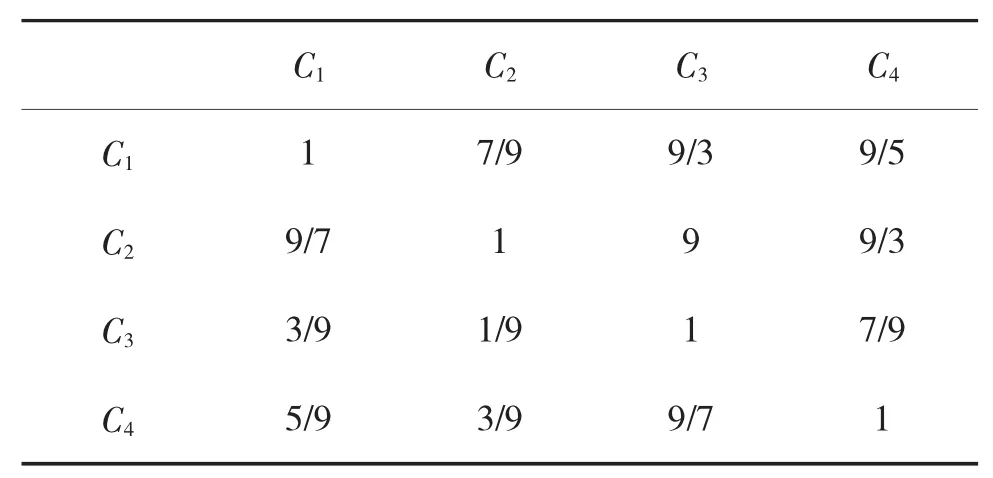
表4 准则层1对射击有利度的比较判断矩阵

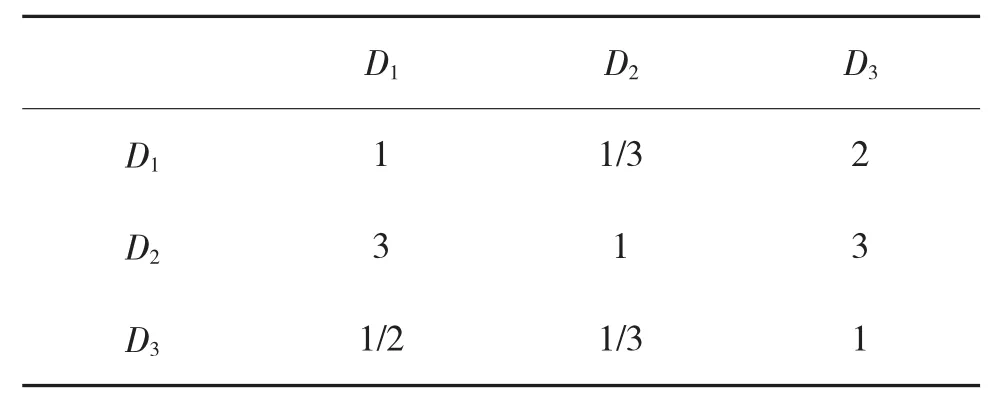
表5 准则层2对射击精度的比较判断矩阵

其中C1表示射击精度，C2表示有效射击时间，C3表示穿越次序，C4表示被弹面积，D1表示目标高度，D2表示目标速度，D3表示航路捷径，利用归一化方法将比较判断矩阵转化为如表6、下页表7所示的模糊矩阵。

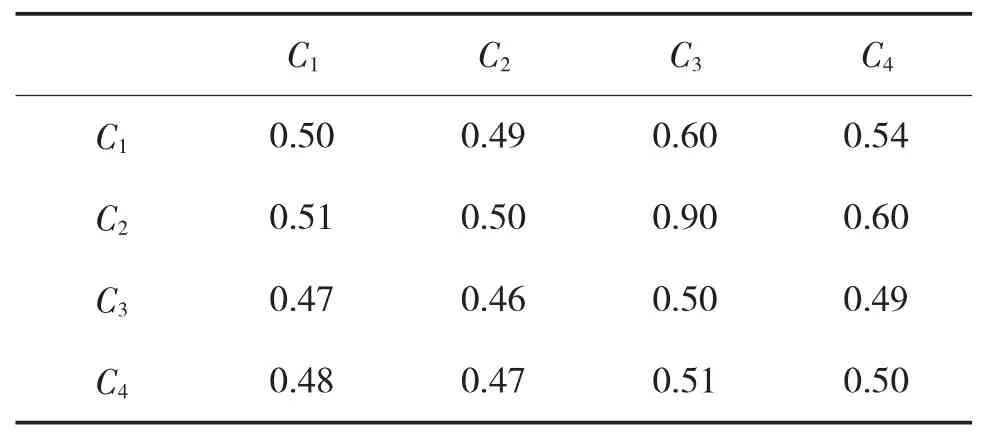
表6 准则层1对射击有利度的模糊矩阵

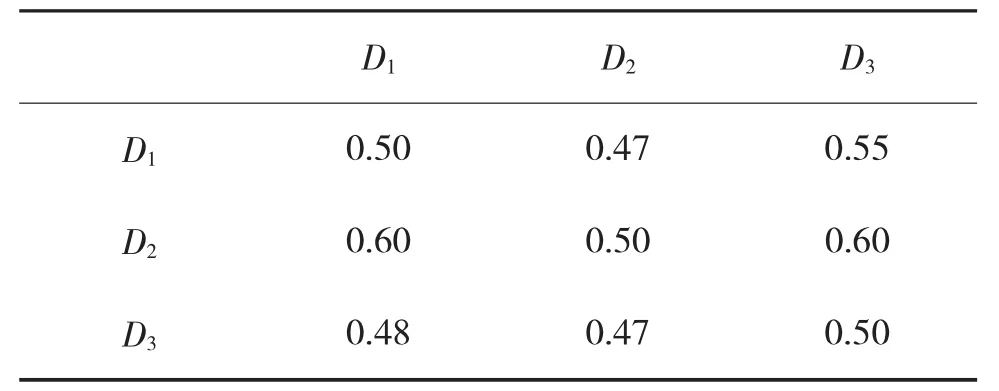
表7 准则层2对射击精度的模糊矩阵

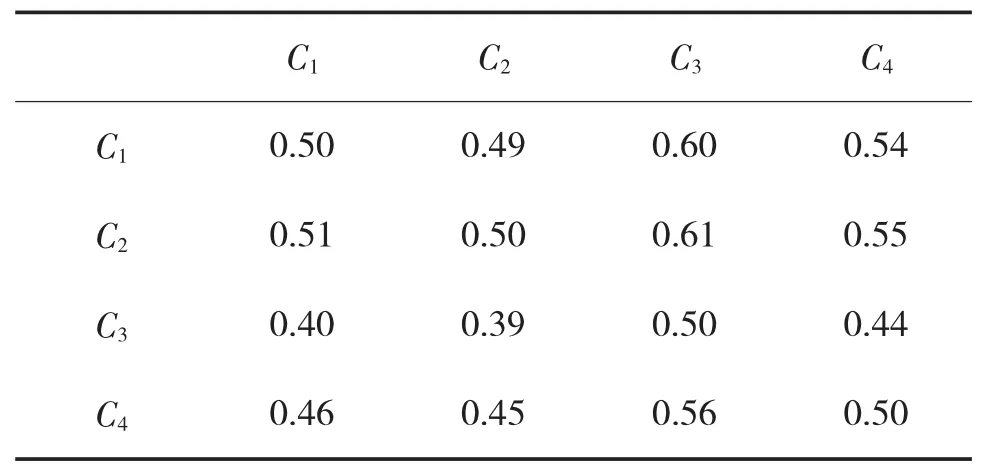
表8 准则层1对射击有利度的模糊一致矩阵

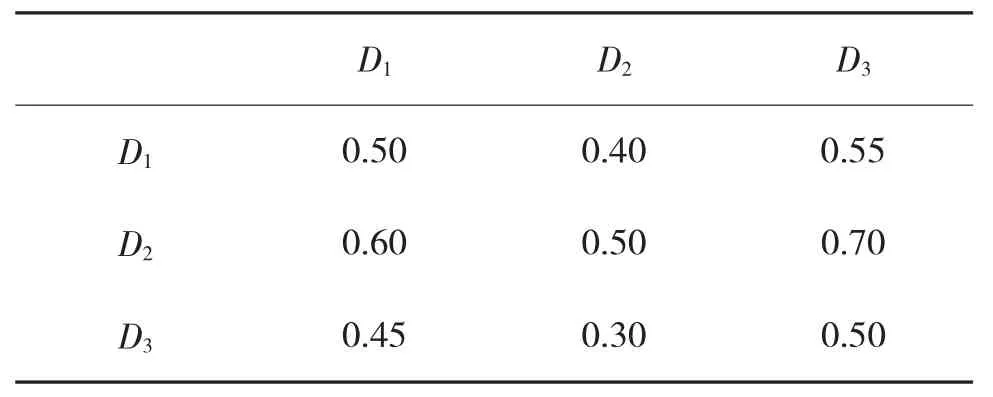
表9 准则层2对射击精度的模糊一致矩阵

2.2.2 计算射击有利度

计算射击有利度需要首先计算准则层相对于其目标的效用，即准则层对其目标的影响力度的大小，这里使用权重表示。使用ωi表示第i个因子的权重。比较判断矩阵一般使用特征值法求解权重。而对于模糊一致矩阵，可以推导出其权重数值满足：

其中rij表示模糊一致矩阵中的第i行第j列元素，a是一个调节因子，其范围是（0，0.5]，其大小表示人们对各个影响因素差异性重视度的大小，本文将a的取值为0.5。求解可得两种矩阵的权重如表10、表11所示。

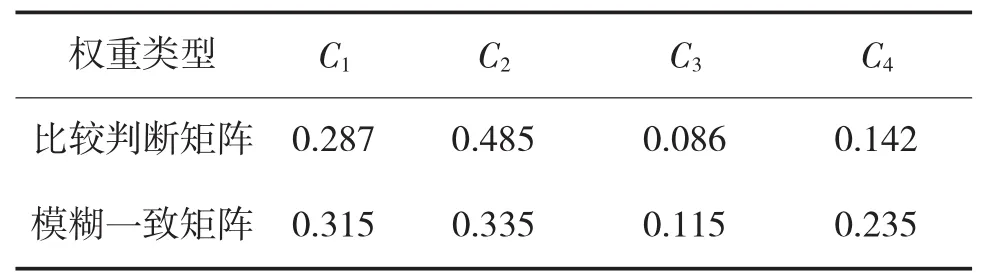
表10 准则层1对射击有利度的权重表

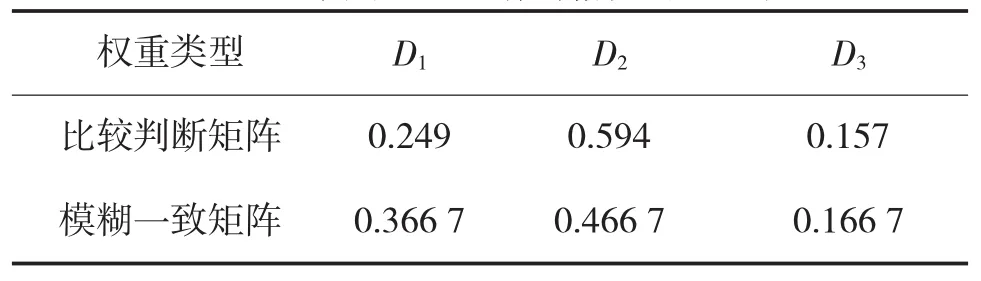
表11 准则层2对射击精度的权重表

可以看出，虽然在数值上，两种矩阵所得的权重数值不同，但是在整体的起伏上，其结果大致相似。

为了得到射击有利度，首先从文献[1]获得空袭兵器的参数，如表12所示。

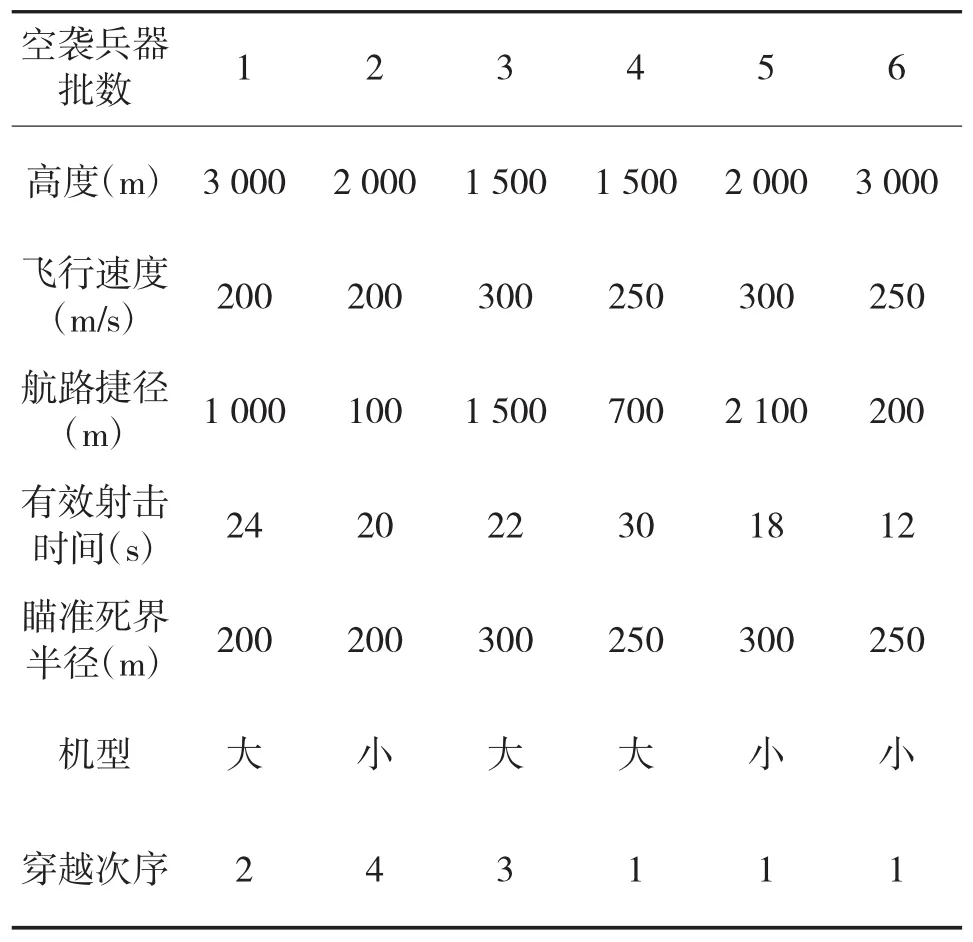
表12 6批不同空袭兵器的部分参数表

利用原文献中的效用方法将这些数据做归一化处理可得下页表13所示。

将目标高度、目标速度和航路捷径与其对应的权重相乘后求和可得到射击精度的效用值，如表14所示。

使用同样的方法对射击精度、有效射击时间、穿越次序和目标类型做处理可得出防空火炮对各个批次空袭兵器的射击有利度，如表15所示。

可以看出，这两种方法得出一致的排序，而且在具体的数值上差别不大。但是使用模糊一致矩阵在计算复杂度上减小了，同时在检验一致性和矩阵修正两方面有了很大的简化。

3 结论

模糊层次分析法针对传统的层次分析法存在的计算复杂度高，一致性判断概念相对模糊以及和人类的思维不符，比较判断矩阵数据的限定缺乏依据，一致性调整复杂的问题给出了改进，本文一方面从理论上给出了模糊层次分析法的优越性，另一方面使用实例，使用两种方法生成数据并进行了对比，证实了模糊层次分析法取得了和层次分析法一致的结果。综合这两方面可知模糊层次分析法具有更好的实用性。

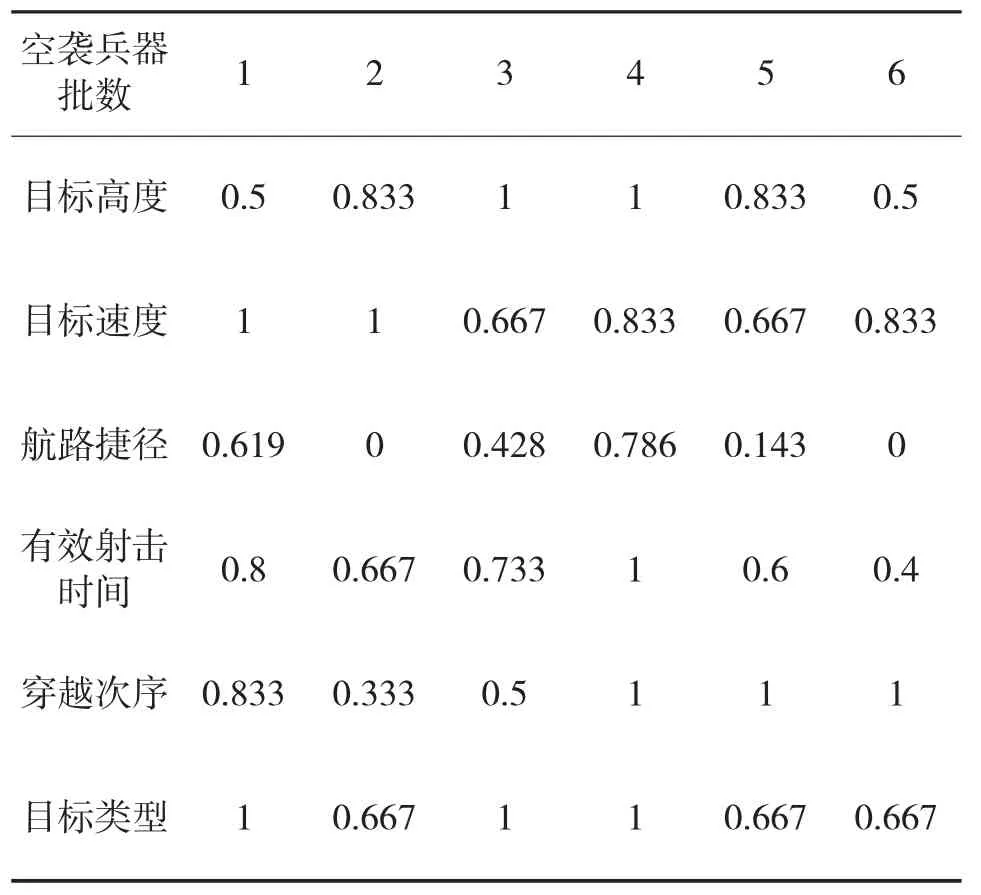
表13 6批不同空袭兵器的归一化数据

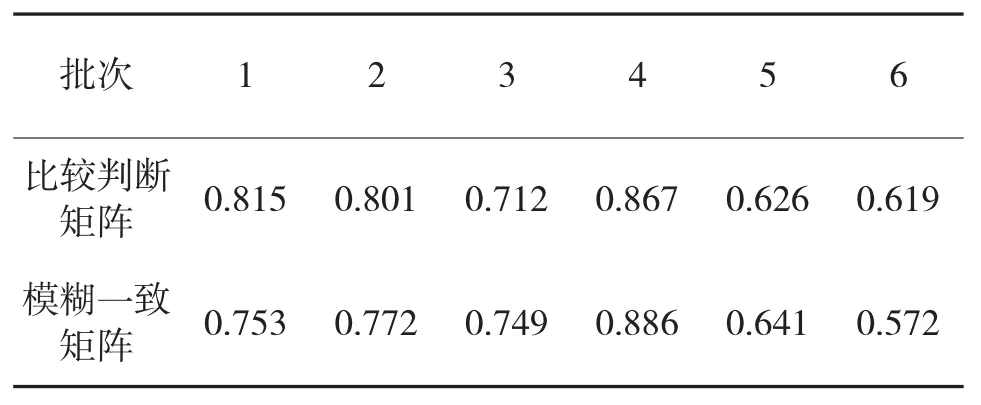
表14 两种不同方法得出的射击精度效用值

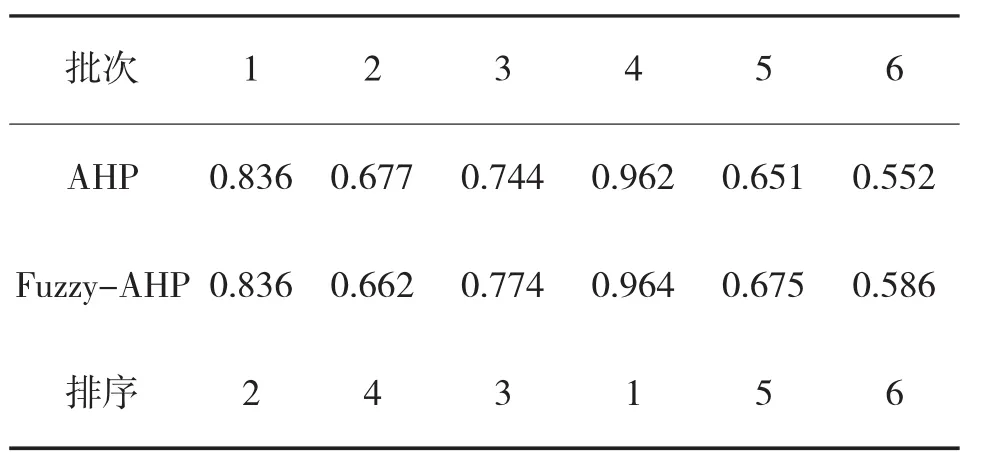
表15 两种不同方法得出的射击有利度