一种基于回旋曲线的局部路径规划方法*

苏治宝，赵熙俊，朱 森，张浩杰

（中国北方车辆研究所，北京 100072）

0 引言

对于地面机器人而言，路径规划是基于一定的优化准则，在有障碍的环境中生成从指定起始位置到达目标位置无碰撞运动轨迹的过程。根据规划范围不同，路径规划分为全局路径规划和局部路径规划。其中，全局路径规划是主要基于先验信息（例如地图），为地面机器人找到到达目标位置最佳路径的过程，而局部路径规划则根据基于平台即刻所采集的环境感知传感器数据建立的地图，规划当前的可执行路径。

目前常用的局部路径规划方法有最短路径法、向量场直方图（VFH）法[1]、曲率速度法（CVM）[2]、势场法[3]、基于回旋曲线的方法[4]等。其中，Dijkstra和A*算法是典型的最短路径方法，这类方法将地图转化成代价图进行搜索，获得最短路径，但获得的路径没有考虑平台的运动约束，无法保证其可执行性，且计算时间相对较长，只适用于低速平台。向量场直方图法以射线为基本路径模型，根据各个方向上存在障碍的概率确定行驶方向，这种方法不适用于阿克曼转向平台，且规划距离短，容易陷入局部极小。曲率速度法将障碍地图转化为3D（旋转速度、平移速度和到障碍的曲线距离）配置空间，并利用曲率将旋转速度和平移速度关联起来，按照一定的目标函数获得具有适当大小曲率的轨迹，这种基于曲率的方法只适合于低速导航。目前使用较多的还有基于特定数学模型（例如多项式函数）的路径规划方法[5]。这类方法中，路径用特定数学模型表示，以运动学或动力学约束为边界条件，确定模型参数。预先生成一簇备选轨迹，根据地图可通行状况和某种优化准则，选择可执行路径。

本文在参考相关文献基础上，针对某轮式阿克曼转向机器人平台，研究了基于回旋曲线路径模型的局部路径规划方法，介绍了该方法的基本实现过程，对关键步骤进行了说明，并利用仿真系统验证了这种方法，最后给出了研究结论。

1 基本方法介绍

基于回旋曲线路径模型的局部路径规划算法由两部分组成：离线部分和在线部分。

其中，离线部分在机器人运行之前完成，主要通过轨迹空间与栅格单元映射关系建立搜索图，基本过程如下：

1）根据机器人阿克曼转向约束，在控制量空间计算所有可能的回旋曲线轨迹，建立轨迹空间；

2）根据预瞄距离，在机器人前方区域离散生成一系列节点，利用通过节点的各轨迹之间的连接关系，确定节点之间的连通关系；

3）获得并保存局部地图各单元与各轨迹索引之间的映射关系，即通过地图某单元有哪些轨迹，某条轨迹上有哪些地图单元，建立搜索图。

在线部分是在机器人运行时完成，主要根据搜索图和环境模型按照某优化准则采用A*算法搜索获取最优路径，基本过程如下：

1）根据轨迹与地图单元的映射关系，结合当前地图的障碍分布情况，在轨迹空间里排除与障碍物发生碰撞的轨迹，获得可行轨迹空间；

2）在可行轨迹空间构建的搜索图中，采用A*算法寻找连通机器人当前位置与当前目标节点位置之间的最优路径。

2 离线算法

2.1 基于节点构建回旋曲线轨迹空间

2.1.1 节点位置的确定

如图1所示，以地面机器人当前位置为圆心，在距离机器人平台为10 m和20 m的弧线上各选择46个节点，节点位置与该节点相对于平台的方位角有关。选取节点位置的原则是“中间密，两边疏”，其原因是：中间对应平台希望行驶的路径方向，“中间密”可以保证规划的路径避让障碍物之后尽可能回到希望行驶的方向上；“两边疏”考虑到平台很少行驶到两边区域，只有当中间区域被障碍物全部占据没有可行路径的情况下平台才向两边行驶。

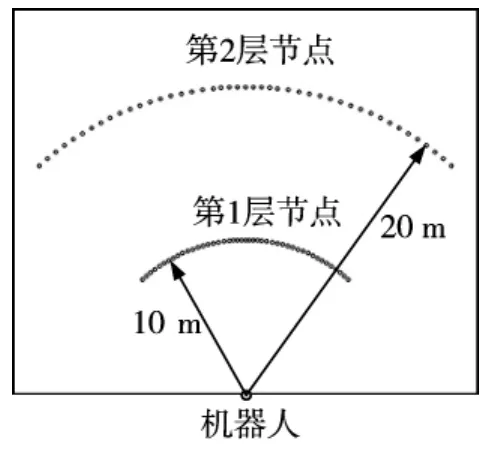
图1 节点分布示意图

2.1.2 生成各层轨迹

图2 车辆运动模型

对于阿克曼转向的轮式平台而言，假定Δt时间间隔内前轮偏角变化率和速度为定值，那么该段行驶轨迹为回旋曲线，平台运动模型为

其中，（x，y）为平台位置坐标，θ为航向，δ为前轮偏角，vf为行驶速度，Δt为时间步长。

在离线算法中，计算回旋曲线轨迹的参数包括平台行驶速度、当前前轮偏角、前轮偏角变化率、计算步长、回旋曲线段数（即轨迹有几段组成）、计算时间等。从理论上，只要对参数的离散化程度足够密，所产生的回旋曲线就是阿克曼转向平台实际可能行驶的所有轨迹。然而由于时间消耗约束，必须对各参数进行合理的离散化处理。

1）行驶速度

在0到12 m/s车速范围内，以步长2 m/s离散化车速，因此，速度数量为6。

2）前轮偏角

最大前轮偏角取30°。离散化时，前轮偏角间隔取1.5°，则共有41个前轮偏角。0～40的序号对应于-30°～30°。

3）前轮偏角变化率

前轮偏角变化率，取决于自动转向执行机构及其控制系统。前轮偏角变化率取7个值，即-30°/s～30°/s，步长为 10°/s。

4）计算步长

计算步长与速度有关，计算步长=0.2/速度。

5）回旋曲线段数

选择最多5段回旋曲线来描述平台前方20 m内的行驶轨迹。

6）计算时间

每段回旋曲线段的计算时间最多为40个周期，计算结束条件为是否满足轨迹长度及航向约束。整条回旋曲线轨迹的计算是否结束取决于轨迹总长和段数。

图3 layer02、layer01、layer12 轨迹

轨迹的生成采用深度优先搜索算法的思路，即由顶节点开始计算，获得一条子轨迹，再以子轨迹末端为起点继续计算，直到达到满足计算结束条件。所获得的所有轨迹都起始于机器人当前位置，止于第2层节点，因此，称为layer02轨迹。

根据轨迹是否通过第1层节点和第2层节点，从layer02轨迹中获取起始于机器人当前位置、止于第1层节点的轨迹集合layer01，获取起始于第1层节点、止于第2层节点的轨迹集合layer12。

2.1.3 生成不同速度和初始前轮偏角下的轨迹空间

为了提高搜索效率，需要将所生成的轨迹空间按照不同速度和初始前轮偏角进行组织和保存，这通过按照速度和初始前轮偏角从layer01和layer12轨迹中进行索引而离线获取。图4为不同速度下前轮偏角为6°时的轨迹空间示例。

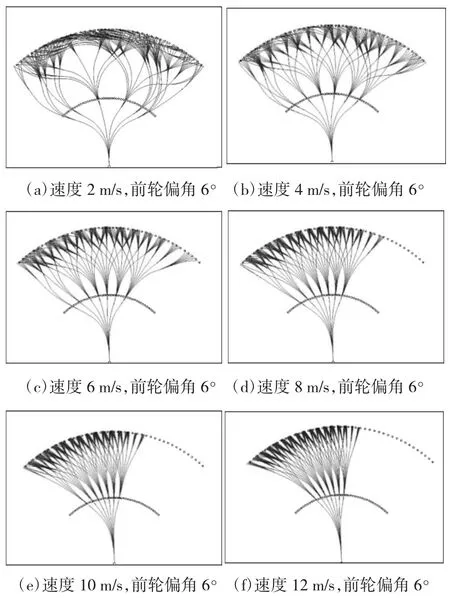
图4 不同速度下的轨迹空间示例

2.2 生成地图单元-轨迹映射表

假设环境地图采用占有栅格形式表示。为了判断轨迹上是否有障碍，需要确定轨迹所通过的栅格单元索引。利用几何计算方法，确定轨迹上离散点位于哪一个栅格单元。需要说明的是，为了确保平台行驶安全，不同的车速下规划的路径有一定的宽度，速度越快，路径越宽，在确定轨迹所通过栅格单元时要考虑路径宽度。轨迹通过哪些栅格的结果按文件的形式保存。

另外，为了减小搜索空间，需要知道每个栅格单元有哪些轨迹通过的信息，这通过反转轨迹通过哪些栅格单元而得到，将这些信息以文件形式保存。

3 在线算法

图5 局部路径规划流程图

如图5所示，在线算法实现局部路径规划的基本流程为：

1）初始化搜索图，即根据所定义的节点初始化A*算法使用的搜索图；

2）加载离线阶段已创建的单元-轨迹映射表；

3）从上层规划器获取全局路径，从感知模块获取局部地图，以及机器人当前位姿；

4）由航路点管理模块确定当前规划周期的目标点；

5）根据当前目标点，依据一定准则（例如与目标点的距离、相对角度最小等）确定A*算法的当前目标节点；

6）利用环境感知模块提供的局部图地图，更新搜索图中各节点的通过成本；

7）利用单元-轨迹映射表和局部地图，排除不能通行的轨迹，获得可行轨迹空间：

8）在可行轨迹空间中利用A*算法搜索可到达目标节点的最优轨迹，最优准则包括轨迹速度、轨迹长度等。

4 仿真实验

为了测试规划算法的规划能力和运行速度，设计了多种场景，开展了仿真实验。仿真条件如下：

1）平台参数：轮距3.2 m，车长4.8 m，车宽2.4 m，初始前轮偏角为零；

2）局部地图尺寸：120×100，分辨率：0.25 m；

3）运算平台：64位台式计算机，Intel（R）Core（TM）i7-6700K CPU@4.00 GHz，16 G 内存，Ubuntu14.04操作系统。

4.1 静态仿真

机器人平台静止，前轮偏角为零，以第2层右侧某节点为目标点，在图中用圆圈所示。图6为4种场景下的仿真实验结果，所规划轨迹的速度分别为：12 m/s、6 m/s、4 m/s、2 m/s，所规划的速度越快，路径越宽；规划耗时分别为 33 ms、116 ms、145 ms、186 ms。

图6 不同场景下局部路径规划结果

图7 无法规划出路径的场景示例

在场景4的基础上，再增加一个障碍，如图7所示，规划器则无法规划出路径。其原因在于，对规划空间采取了离散化处理，其完备性会受到影响。

4.2 动态仿真

在起伏越野环境中，布置若干静态障碍，并给定全局路径，动态仿真机器人从起点到终点的自主导航过程，测试所提出局部路径规划方法的性能。

仿真结果如下页图8所示。其中，图8（a）为仿真场景，图8（b）为给定的全局路径和机器人实际行驶路径，图8（c）为每次局部路径规划的耗时，图8（d）为机器人行驶速度曲线。在自主导航过程中，机器人可以较合理地选择局部路径，每次规划平均耗时37.383 8 ms，平均行驶速度6.842 7 m/s。

5 结论

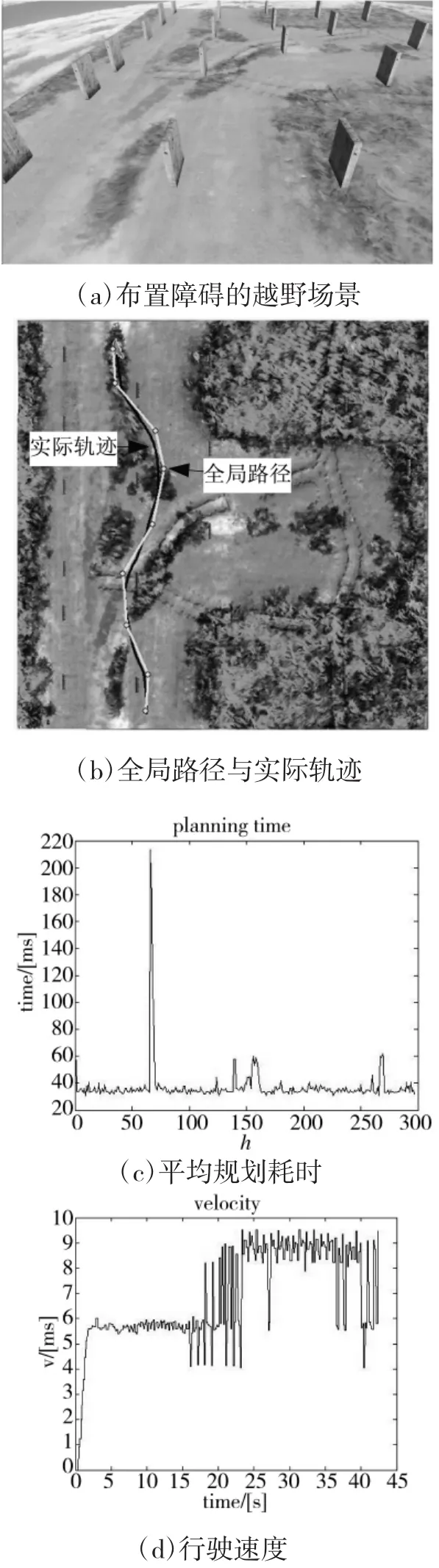
图8 动态仿真结果

本文研究了一种基于回旋曲线路径模型的局部路径规划方法，在离线计算轨迹空间时，由于考虑了平台的运动学特性，因此，所规划的路径具有良好的可执行性；在离线生成地图单元-轨迹映射表时，考虑了平台运行速度，提高了平台行驶安全性。但受回旋曲线模型的约束，所提出的局部路径规划方法只适用于采用阿克曼转向的轮式平台；在根据平台参数预先计算轨迹空间时，对参数进行了离散化处理，影响了这种规划方法的完备性。在未来研究工作中，需要关注两点：一是如何优化组合计算轨迹空间时所用的参数，降低对规划完备性的影响，确保在环境复杂但有路径可行的情况下，规划方法确实能规划出轨迹；而是研究规划完备性与规划耗时之间的关系，确保同时满足规划方法实用性要求与平台运行实时性需求。