基于单快拍数据的嵌套阵列DOA估计算法

韩佳辉，毕大平，陈 璐

（国防科技大学电子对抗学院，合肥 230037）

0 引言

波达方向（Direction of Arrival，DOA）估计是阵列信号处理的研究热点，也是雷达对抗侦察领域重要研究方向。随着现代信息技术的发展，战场电磁环境日益复杂，侦察天线接收的有效数据往往是少量的几次快拍数据，需要长时间数据积累的测向算法如 MUSIC（Multiple Signal Classification）[1]算法越来越难以满足作战需要，所以采用单快拍数据进行DOA估计[2-5]成为一种发展方向。文献[1]结合空间平滑技术实现单快拍数据角度估计，但是算法损失了阵列孔径并且运算量较大。文献[2]直接利用阵列接收数据构造Toeplitz矩阵作为协方差矩阵，增加了实时性。但是算法抗噪声干扰能力差，在低信噪比的情况下估计误差较大。文献[3]在文献[4]的基础上，在对阵列接收单快拍数据进行相关处理后重构Toeplitz矩阵，提高了抗噪声干扰能力。文献[5]直接利用单快拍阵列接收数据构造长方形伪协方差矩阵，通过奇异值分解实现DOA估计，突破了协方差矩阵为方阵的限制，模型更具有一般性。

但是以上单快拍DOA估计算法仅仅在均匀线阵基础上进行研究，对非均匀阵列研究相对较少。半波长均匀线阵存在阵列孔径不高的缺点，只能通过增加阵元的方式提高阵列孔径，但是增加阵元大大增加了硬件成本。相比于阵元数目相同的均匀线阵，嵌套阵列具有更大的阵列孔径。在相同的阵列孔径下嵌套阵需要的阵元数目更少，节约了硬件成本。文献[6-9]利用嵌套阵列进行DOA估计，增加了测向精度。但是这些算法都依赖多快拍数据，实时性较差。因此，本文提出了针对嵌套阵列的单快拍数据DOA估计算法。算法将嵌套阵列和单快拍数据的优点结合起来，利用单快拍数据构造两个Toeplitz矩阵，通过两次谱峰搜索得到高精度无模糊DOA估计。仿真实验通过与文献[3]对比进一步验证了算法的有效性。

1 信号模型

假设有阵元数目为M的二级嵌套线阵，结构如图1所示，由两个均匀线阵（ULA）构成，每级ULA阵元个数相同为 M/2。阵元位置坐标为 z=[z1，z2，…，zM]，其中子阵1阵元间距d1=/2，子阵2阵元间距d2=/2。P个波长为的远场窄带不相关的信源以来波方向 θ（ii=1，2，…，P）入射到该阵列上，阵列的接收信号为：

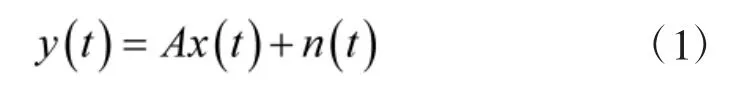
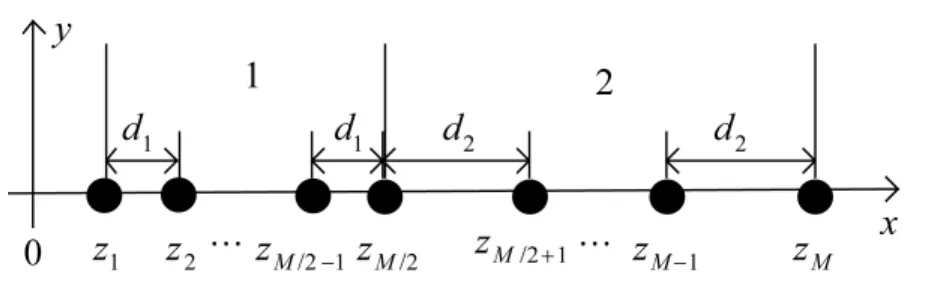
图1 二级嵌套阵

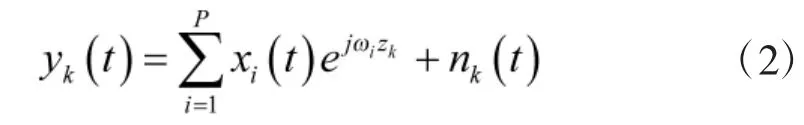
其中，nk（t）为第k个阵元的加性高斯白噪声。

2 嵌套阵列DOA估计方法

2.1 Toeplitz矩阵重构

传统的子空间类算法是通过接收信号的协方差矩阵进行特征值分解得到信号子空间和噪声子空间，然后进行DOA估计。但是接收信号为单快拍数据时，导致阵列协方差矩阵的秩小于信源个数，此时此类算法失效。文献[3]直接利用阵列接收的单快拍数据重构Toeplitz矩阵，实现了DOA估计。本文在文献[3]的基础上，将Toeplitz矩阵构造方法用于嵌套阵列。利用子阵1和子阵2接收的单快拍数据分别构造如下矩阵：

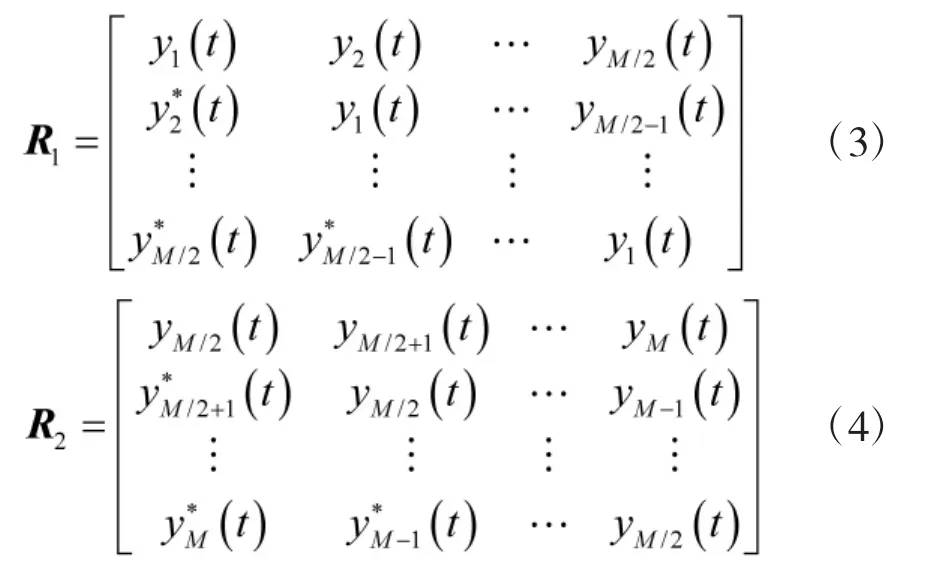
由式（2）及导向矢量a（θi）的特点得

式中，k，j=1，2，…，P（k+j≤Q）则式（3）可以写成

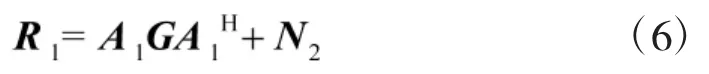
式中

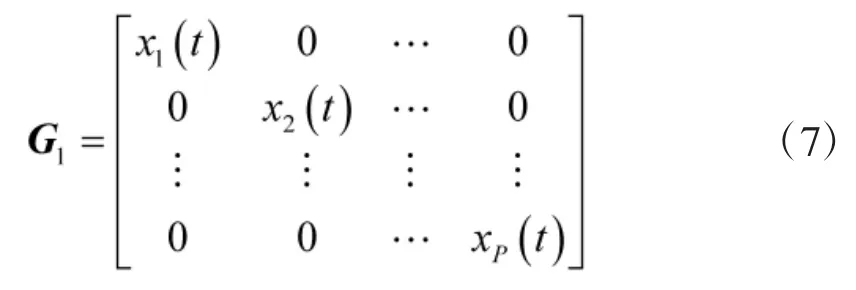
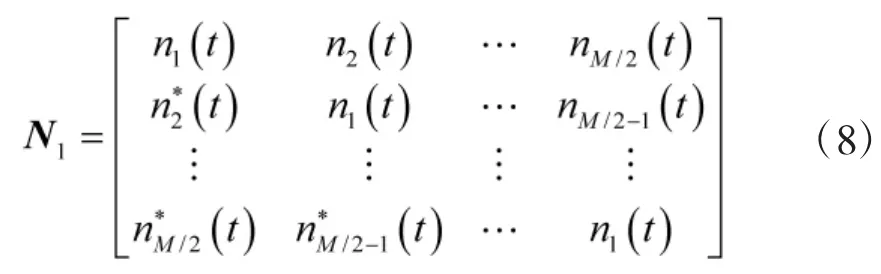
同理式（4）可以写为

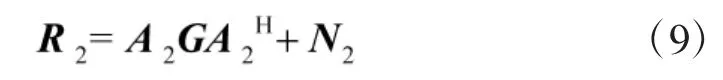
很显然G的秩和入射信号个数P相等。且由于A1为Vandermonde矩阵，所以A1和A1GA1H的秩都为P。即R1可以分解为信号子空间US和噪声子空间UN，同理R2也可以进行特征值分解。

对R1和R2进行特征值分解，结合MUSIC算法进行DOA估计。定义阵列空间谱函数为

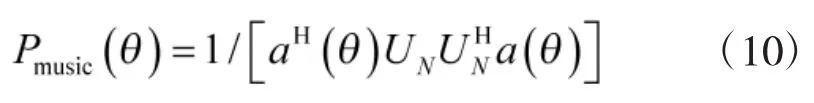
由上式，使θ变化，通过寻找波峰来估计到达角。因为子阵1阵元间距d1=/2，子阵2阵元间距d2=/2。所以，通过R1会得到低精度无模糊的测向结果，通过R2会得到高精度有模糊的测向结果[10]。若想获得高精度无模糊的测向结果，则需要进行解模糊处理。本文采用二次搜索法[11]解模糊。

2.2 二次搜索法解模糊

假设入射信源个数P=1。二次搜索法的基本思想是首先利用子阵1接收的单快拍数据构造的矩阵R1运用MUSIC算法，测出信号来向θ1。然后在θ1的两侧设置新的搜索区间，使搜索区间内只包含真实谱峰。最后利用子阵2接收的单快拍数据构造的矩阵R2运用MUSIC算法，在内进行小步长的二次搜索，得到高精度无模糊的信号来向θ2。此方法的关键就是准确地设置搜索区间，即准确地找出相邻谱峰对应角度之差2Δθ。

将式（11）化简得

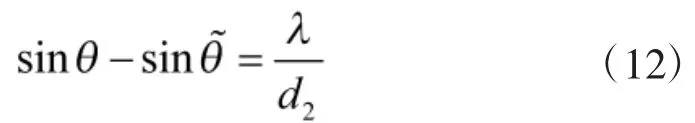
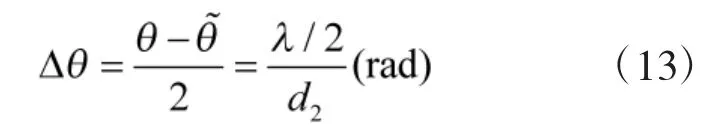
利用子阵2接收的单快拍数据构造的矩阵R2运用MUSIC算法，在内进行小步长的二次搜索就可以得到高精度无模糊测向结果。

2.3 算法步骤

综上，本文算法的实现步骤如下：

步骤1 直接利用嵌套阵列两个均匀子阵接收的单快拍数据构造Toeplitz矩阵R1和R2。

步骤2 矩阵R1进行特征值分解，结合MUSIC算法，搜索出低精度信号来向θ1。

步骤3 将子阵2阵元间距d2代入式（13），确定二次搜索区间。

步骤4 利用矩阵R1进行特征值分解，结合MUSIC算法在搜索得到高精度无模糊测向结果。

3 仿真实验

3.1 算法有效性分析

采用阵元数目M=8的嵌套阵，阵元位置坐标z=[0，1，2，3，4，8，12，16]。一远场窄带信号以 θ1=10°入射，信号波长=2。信噪比SNR=10 dB。采用本文算法得到结果如图2、图3所示。

图2 一次搜索测向结果

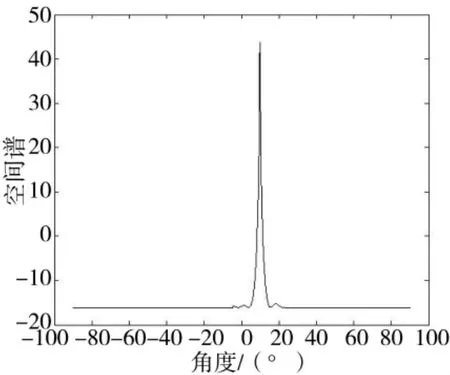
图3 二次搜索测向结果

从图2可以看出，只进行一次搜索时，存在测向模糊。从图2可以看出，经过二次搜索后，模糊角度被消除，实现了无模糊测向。因此，本文算法在嵌套阵列的基础上，利用单次快拍数据成功实现了无模糊DOA估计。

3.2 DOA估计分辨率性能

本文算法采用阵元数目M=8的嵌套阵，阵元位置坐标 z=[0，1，2，3，4，8，12，16]。文献[3]算法采用阵元数目M=8的均匀线阵。阵元位置坐标z=[0，1，2，3，4，5，6，7]。一远场窄带信号以 θ1=0°入射，信号波长=2。信噪比SNR=10 dB，采用本文方法与文献[3]算法得到的结果如图4所示。

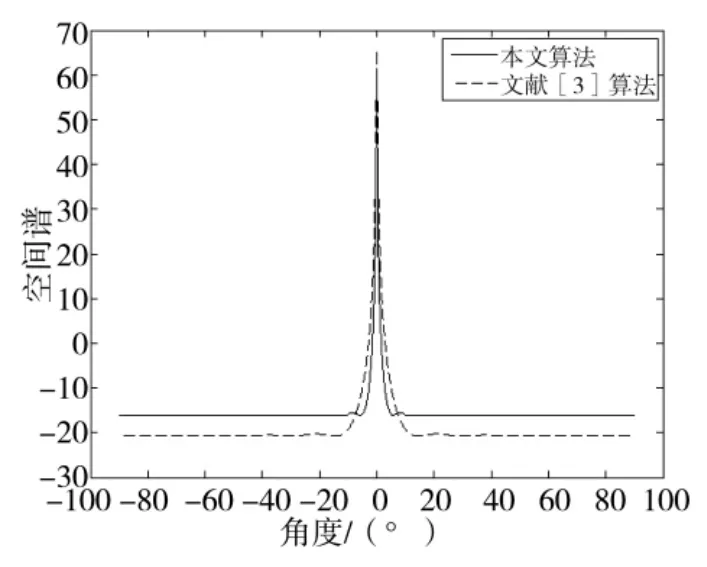
图4 测向结果比较

从图4可以看出，对于单个信号，在阵元数目相同的情况下，本文算法和文献[3]算法都能实现无模糊角度估计，但本文算法空间谱较文献[3]算法拥有更低的旁瓣，估计精度和估计效果更好。

本文算法采用阵元数目M=8的嵌套阵，阵元位置坐标 z=[0，1，2，3，4，8，12，16]。文献[3]算法采用阵元数目M=17的均匀线阵。阵元位置坐标z=[0，1，2，3，4，5，6，7，8，9，10，11，12，13，14，15，16]。一远场窄带信号以θ1=0°入射，信号波长=2。信噪比SNR=10 dB，采用本文方法与文献[3]算法得到的结果如图5所示。

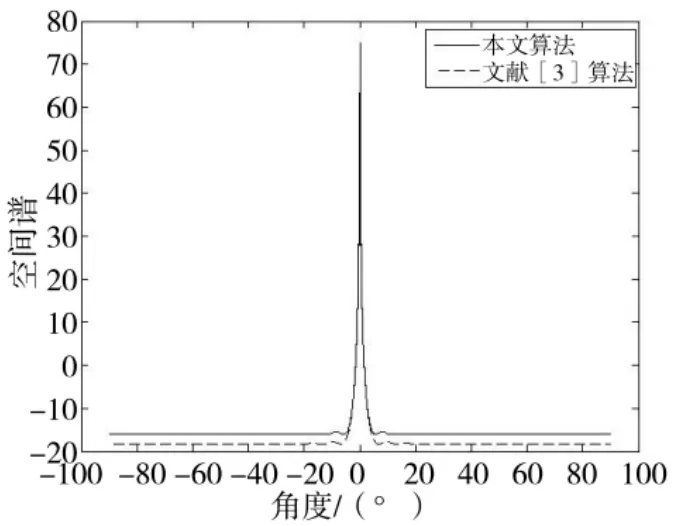
图5 测向结果比较

从图5可以看出，本文算法和文献[3]算法均实现了角度估计，并且空间谱相差不大。但是相比于文献[3]算法，本文算法需要的阵元数目减少一半左右，大大降低了在实际应用中的硬件成本。

3.3 均方根误差和测向成功概率比较

本文算法和文献[3]算法采用阵列与3.2节相同。一远场窄带信号以θ1=0°入射，信号波长=2。信噪比从-5 dB变化到25 dB，每2 dB做300次Monte-Carlo实验。比较信噪比对均方根误差的影响如图6所示。信噪比对估计成功概率的影响如图7所示。

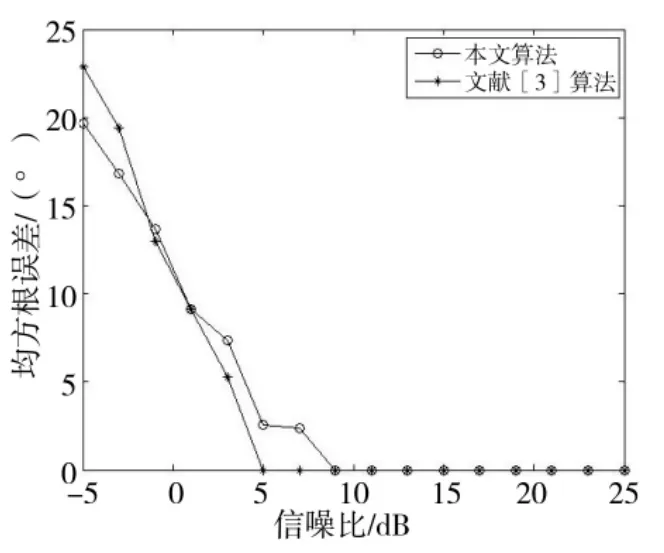
图6 均方根误差随信噪比变化

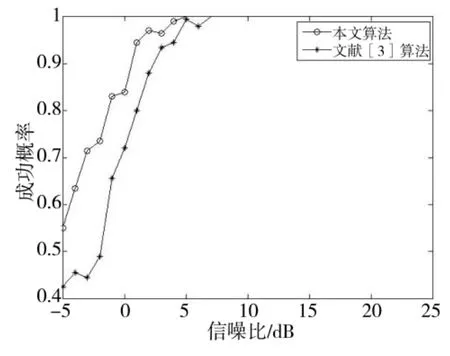
图7 估计成功概率随信噪比变化

由图6看出低信噪比时，本文算法比文献[3]算法拥有更低的均方根误差，随着信噪比增加，两种算法均方根误差趋于相同。由图7可以看出在信噪比较低时，本文算法比文献[3]算法估计成功概率更高。因此，本文算法具有更好的测向性能。

4 结论

针对嵌套阵列DOA估计问题，提出了一种基于单快拍数据的估计算法。该算法将嵌套阵分为阵元间距等于信号半波长和阵元间距大于信号半波长的两个均匀子阵。利用两子阵接收的单快拍数据分别进行Toeplitz矩阵重构，最后通过MUSIC二次搜索算法实现了高精度无模糊DOA估计。仿真实现表明，与文献[3]中单快拍数据算法相比，在相同阵元数目情况下，本文算法测向精度更高，DOA估计性能更好。在相同的阵列孔径下，本文算法需要的阵元数目比文献[3]算法减少一半，大大降低了硬件成本。