基于模糊聚类——拍卖机制的火力协同方法*

王增发，徐克虎，孔德鹏，李灵之

（陆军装甲兵学院，北京 100072）

0 引言

多武器-目标的协同任务分配问题涉及到与战场环境匹配，以及与其他武器平台之间的协同问题，需要根据具体的作战任务和战场态势的变化及时调整，是一个复杂的优化过程。当参与对抗的装备数量较大时，应采用主从决策机制的二次目标分配方法，即根据作战意图、战场价值或威胁度[1]等，先对目标进行集群式武器-目标分配（分组），再进行平台级武器-目标分配。火力协同问题求解方法有遗传算法、模拟退火算法、群智能算法[1-3]等。对于算法的选择，主要是依据攻击代价和效益指标。由于传统的算法在目标分配上存在代价大、时效性差、适应能力低等缺点，难以适应现代战场的作战要求，所以本文对聚类算法[4]进行改进，并结合拍卖算法[5]，提出一种基于聚类—拍卖机制的协同作战任务分配方法。

本文采用模糊均值聚类与拍卖算法相结合的方法，进行合成分队火力协同方法研究。

1 算法简介

1.1 聚类算法

模糊C均值（FCM）聚类算法[6]是一种对数据样本进行模糊分组的方法，通过优化目标函数得到每个对象对分组中心的隶属度，允许样本以一定的隶属度隶属于不同的组。

聚类算法[7-8]是研究指标分类的一种多元统计方法，通过聚类可将性质相近的归为一类。在战场目标的研究中，可根据目标的相对距离、打击范围、作战意图等指标进行聚类。

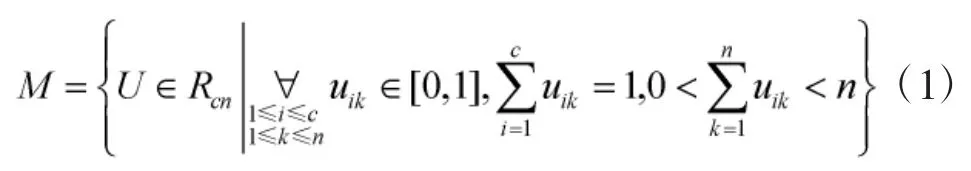
其中，Rcn表示所有实c×n矩阵形成的空间。FCM算法的目标函数为：

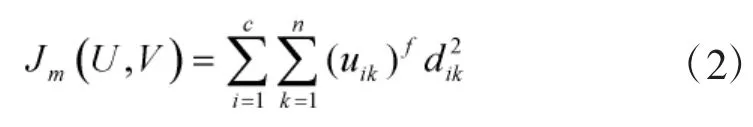
聚类问题就是求满足目标函数的最小解。FCM算法通过对目标函数的迭代优化来取得模糊分类。算法流程如图1所示。

具体步骤为：

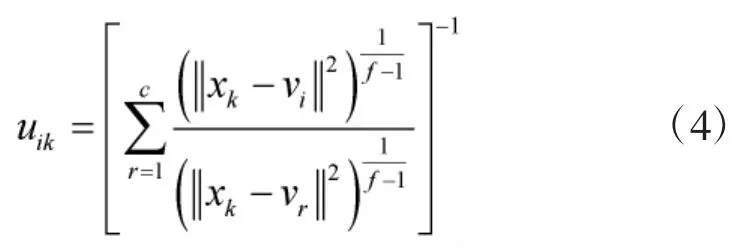
步骤3 根据U（t+1）按下式更新第（t+1）次迭代的中心 V（t+1）

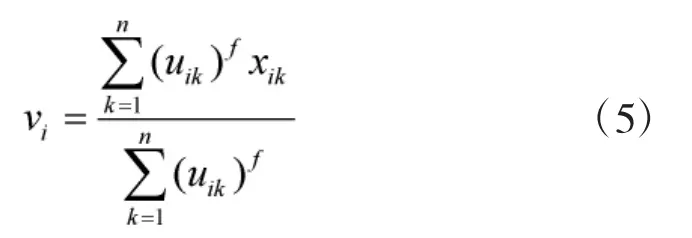
步骤4 比较 V（t）和 V（t+1），若，则算法终止；否则令t=t+1，转至步骤2。

其中，ε为预先设定的正数作为阈值。在算法中，参数f影响分组的模糊性，f越大则分组越模糊，通常取f=2。

图1 聚类算法基本流程

1.2 拍卖算法

拍卖算法[9]在解决分布式的目标分配方面有一定的优势，其无中心节点，鲁棒性、延展性较强，求解相对容易，尤其适应于动态变化、协同要求较高的战场环境。它与模糊C均聚类算法相结合，能够降低多目标协同和非线性协同方面的缺陷，可更好地解决武器目标数量较大的协同任务分配的问题。

拍卖算法由D.P.Bertsekas提出，是用于解决资源或任务分配的常用方法[10]。其基本原理是：将n个物品拍卖给m个买家，假设买家i对物品j期望最大的出价为aij，对物品必须支付的价格是sj，那么其净利润为aij-sj；对每个买家而言，追求的是净利润最大化，即。当每个买家都满意时，这组分配和这组价格达到了平衡。对于整体而言，这样的平衡分配提供了最大总利润，也就达到了整体最优。在本文中，所竞拍的物品即为任务分配方案，每个攻击方的武器平台对所生成的方案进行参数的设置并各自计算价值函数，选择价值最高的竞拍主体。在初始化计算之后随即生成竞拍顺序，启动拍卖过程，轮到竞拍的攻击主体根据其攻击方案进行更新其目标价值函数。所有的竞拍完成后，一轮拍卖结束，得到目标分配方案。在资源允许时，算法生成新的竞拍顺序，开始新一轮的拍卖过程。在资源超出限制时停止运算，得到当前最优的方案。其具体流程如图2所示。

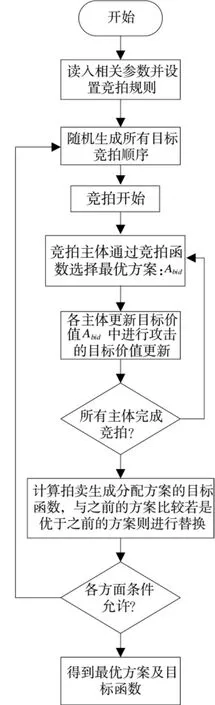
图2 拍卖算法流程

2 基于聚类——拍卖机制的协同任务分配

火力协同，在现代的信息化条件下，以多兵种、多种武器装备为基础的不同作战力量在更加复杂的作战领域，为了共同的作战目的而一起进行的作战行动。

火力协同要求能够有一个统一的指挥中心，在指挥中心的决策指挥下，能够集中优势兵力进行有重点、有选择地攻击目标。并对于整体的战场态势和作战力量有实时的把握，能够结合敌我态势的情况，及时地将我方作战力量进行优化分配，以完成协同作战任务。

2.1 协同任务分配的数学模型

本文针对多目标协同任务分配问题[11-12]进行研究，主要考虑各个武器目标的打击能力、速度、位置等因素，和目标的价值、毁伤代价以及作战环境对任务分配的影响等，并基于此构建了多目标协同任务分配模型，如图3所示。通过双层任务模型分配，以达到减少战斗损失、最大程度地杀伤敌方的目的。

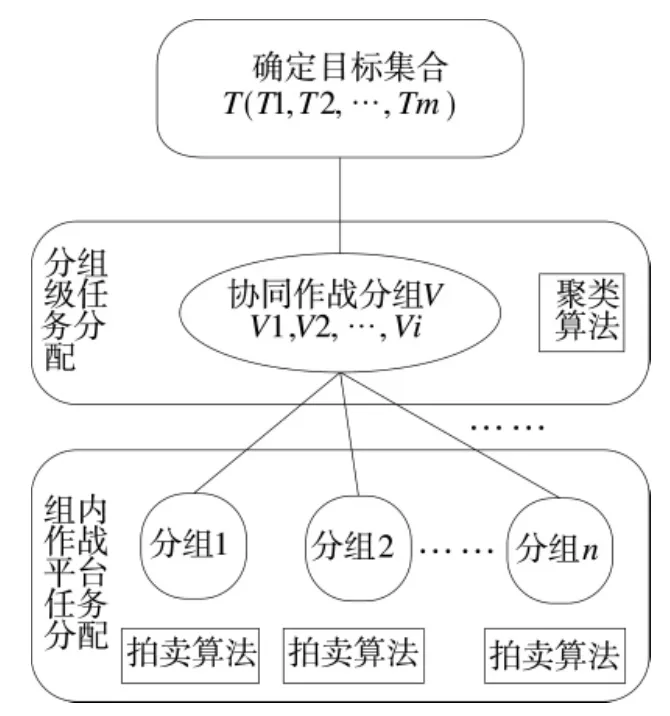
图3 聚类——拍卖算法流程

其中，Nmax表示第j个目标受到的最多攻击武器数目。

1）摧毁目标效益

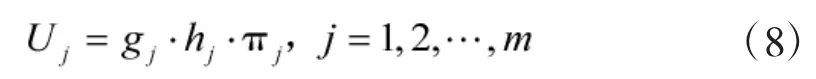
其中，gj为目标Tj的战场价值（威胁度），表示其战略重要程度；hj为目标所在的战场环境指标；πj为目标Tj被摧毁的概率函数。

2）攻击目标代价

其中，αi为损耗概率；ri为作战能力指标，与机动能力、装载弹药有关。

3）目标函数

根据目标摧毁效益和攻击代价可得单武器目标函数：

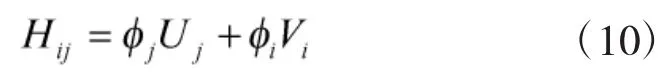
根据目标摧毁效益和攻击代价可得目标函数：

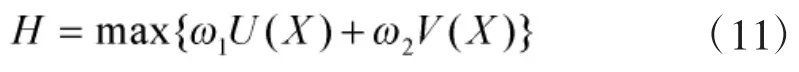
其中，ω1、ω2分别为目标效益函数权系数、攻击代价函数权系数。

2.2 流程简介

在考虑评估要素的武器目标分组中，评估要素向量用评估要素集合形式来表示：

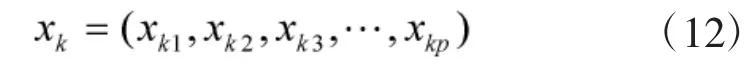
基本步骤如下：

Step 1 初始化或更新分组个数：初始化时，c=2；更新时，c=c+1。设定武器单元的最大个数C0；

Step 2 分两组时，选择2个距离最远的平台作为初始分组中心，分组组数再增加时，应将距已选好的分组中心最远的武器平台作为下一个初始分组中心。

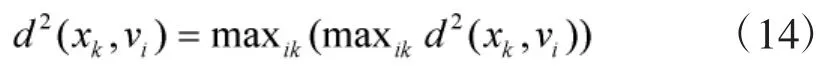
Step 3 更新每个目标对各组的隶属度uik，根据隶属度的大小将设备归属于隶属度最大的组，完成一次分组。

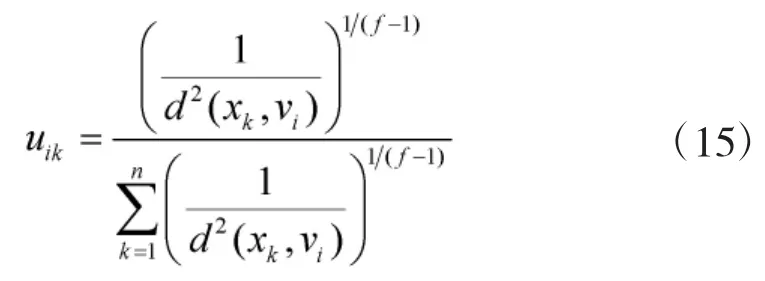
Step 4 根据新的隶属度，计算各组的分组中心

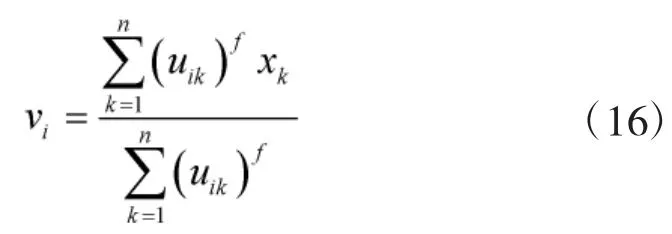
Step 5 计算聚类有效性指标Jmax。

Step 6 重复Step3～Step5，直到有效性指标不再减小，得到最小的聚类有效性指标；

Step 7 重复 Step1～Step6，直到 c=C0；

Step 8 选择具有最小聚类有效性指标的分组作为最优分组；

Step 9 读入聚类分组ci和xk的相关参数，随机生成竞拍顺序，开始拍卖；

Step 10 轮到竞拍目标xk，计算竞拍函数，并选择最好的方案，进而更新各个目标新价值；

Step 11 判断是否所有xk完成竞拍和资源限制；

Step 12 获得组内分配结果。

3 实例分析

假设战场环境中有20个不同类型的目标。基于此，首先计算目标价值矩阵，需要考虑到目标打击范围p1、目标价值p2、目标的武器弹药水平p3等，具体信息如表1所示。

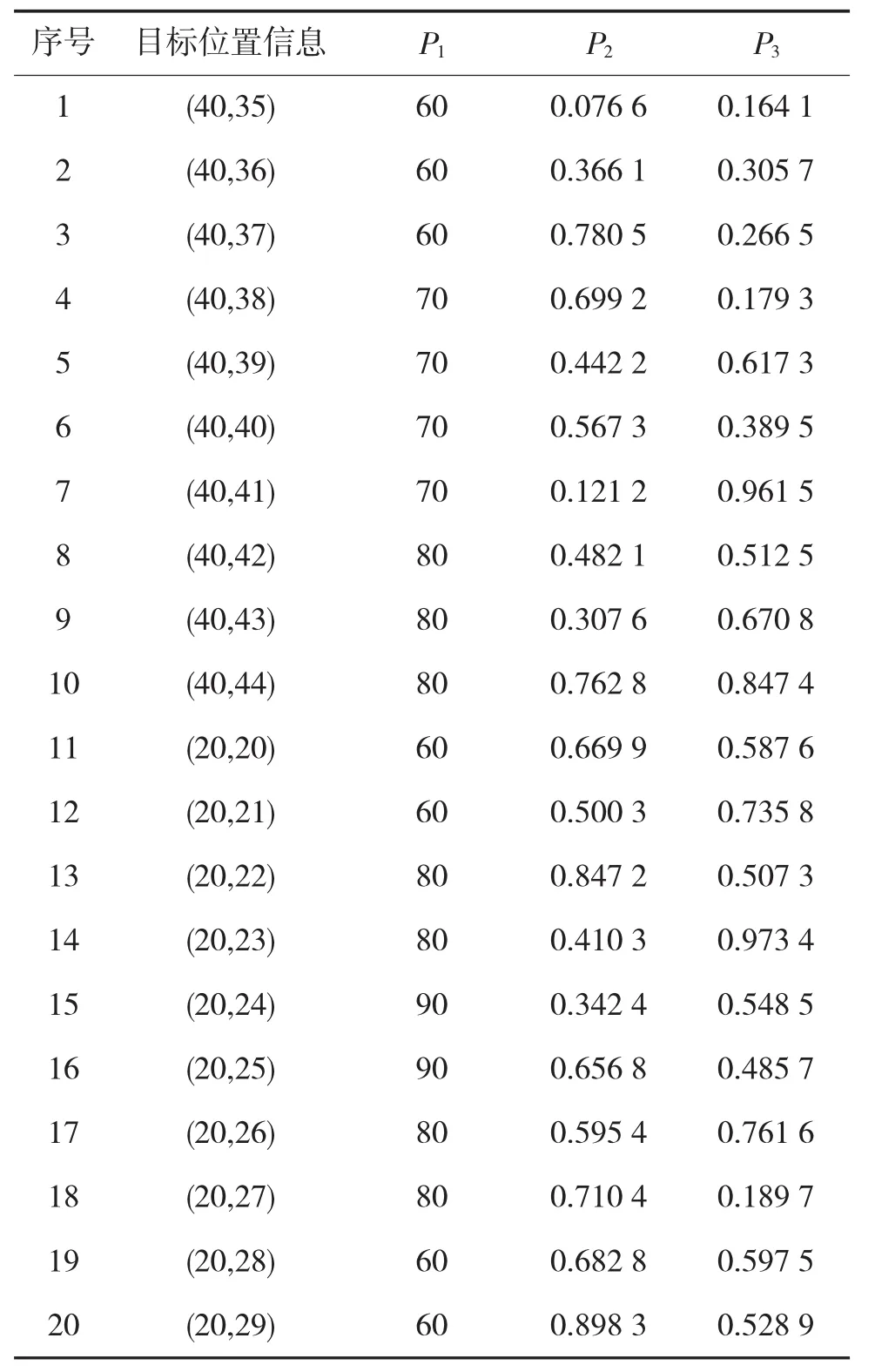
表1 目标信息列表

首先，在不考虑协同的情况下，只利用拍卖进行分配的方法，进行简单的任务分配，使得每一个武器对应于一个目标。获得分配结果，如表2所示。

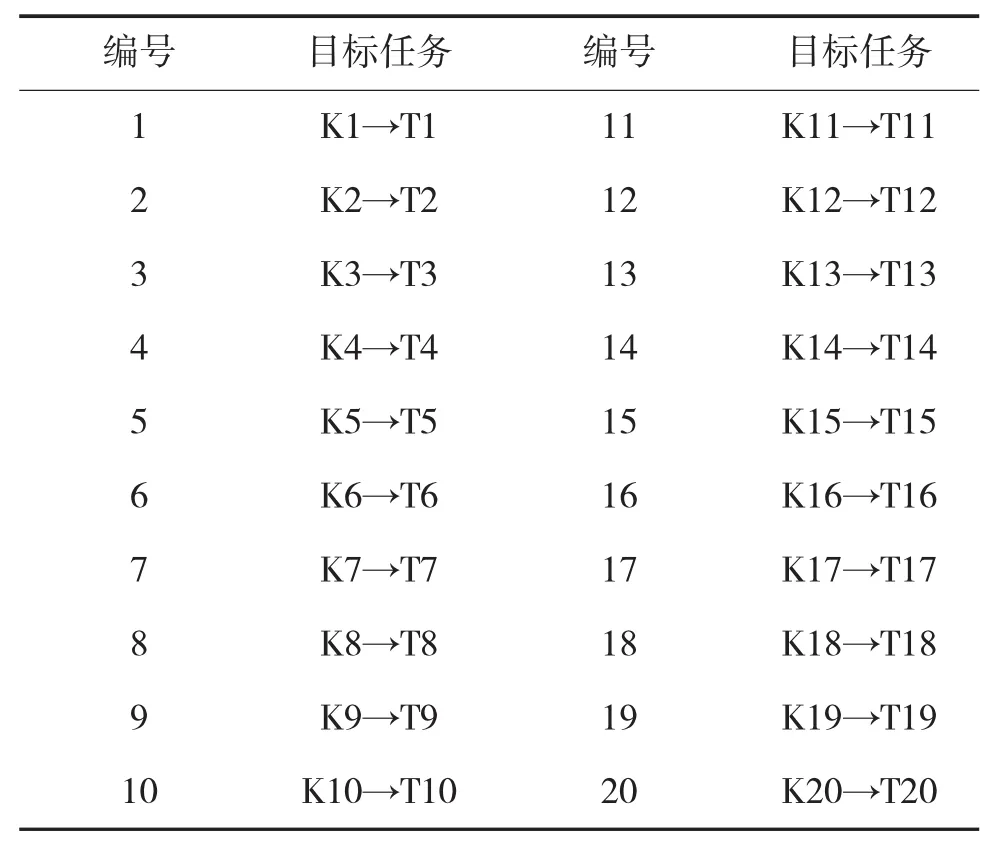
表2 传统拍卖算法的任务分配结果

如表4所示，可发现每个武器对应于一个目标，需对应着逐个目标进行计算，运算过程比较漫长，任务的分配在实际操作中会产生很大的困扰，使得目标分配的难度增大。

其次，运用模糊聚类拍卖的方法进行分配。先进行模糊C聚类操作，聚类效果如图4所示。

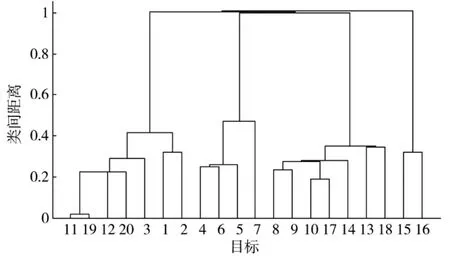
图4 目标聚类分组结果

对20个目标进行聚类分析，得到如图4所示结果：1、2、3、11、12、19、20 划分为一组；4、5、6、7 划分为一组；8、9、10、13、14、17、18 划分为一组；15、16划分为一组。

再通过拍卖算法进行组内的分配，例如在第1组内进行目标的具体划分，按照1.2节所示算法流程进行组内分配，例如第1分组的信息如表3所示。

得到分配结果如表4所示。

通过分配结果可看出，距离因素在任务分配中能够产生更大的影响，之后就是目标价值的影响，因而由更多的武器攻击目标T1、T2和T20。

通过实验对比，可得知基于聚类——拍卖机制的协同任务分配方法在通过分级地进行任务划分后，能够提高分配效率，加快作战的进程。本文的协同任务分配方法能够比无协同的简单火力分配更有优势。

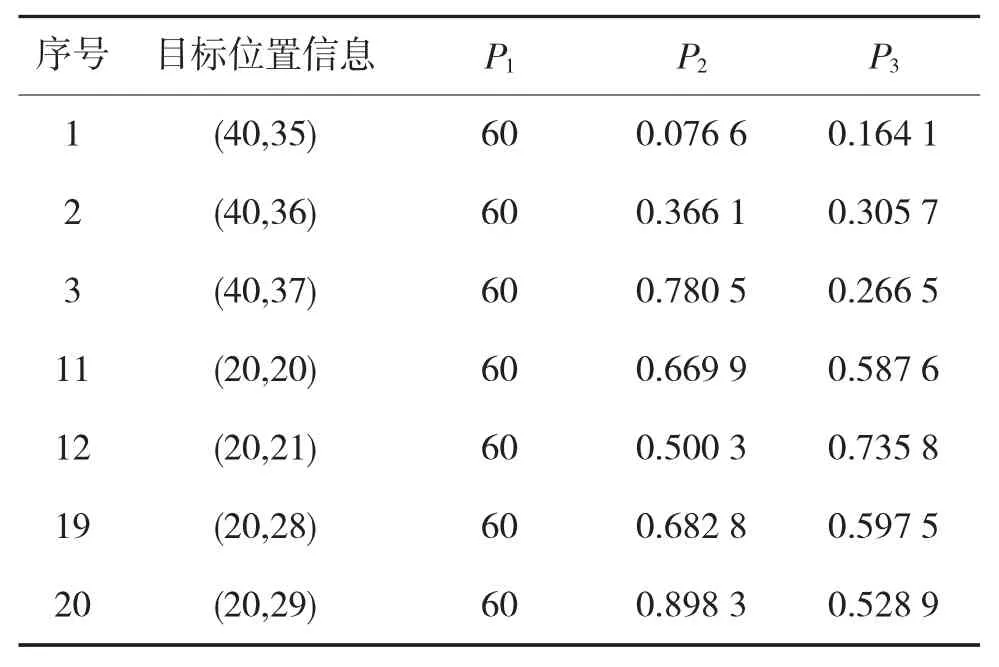
表3 聚类后第1分组的“成员”

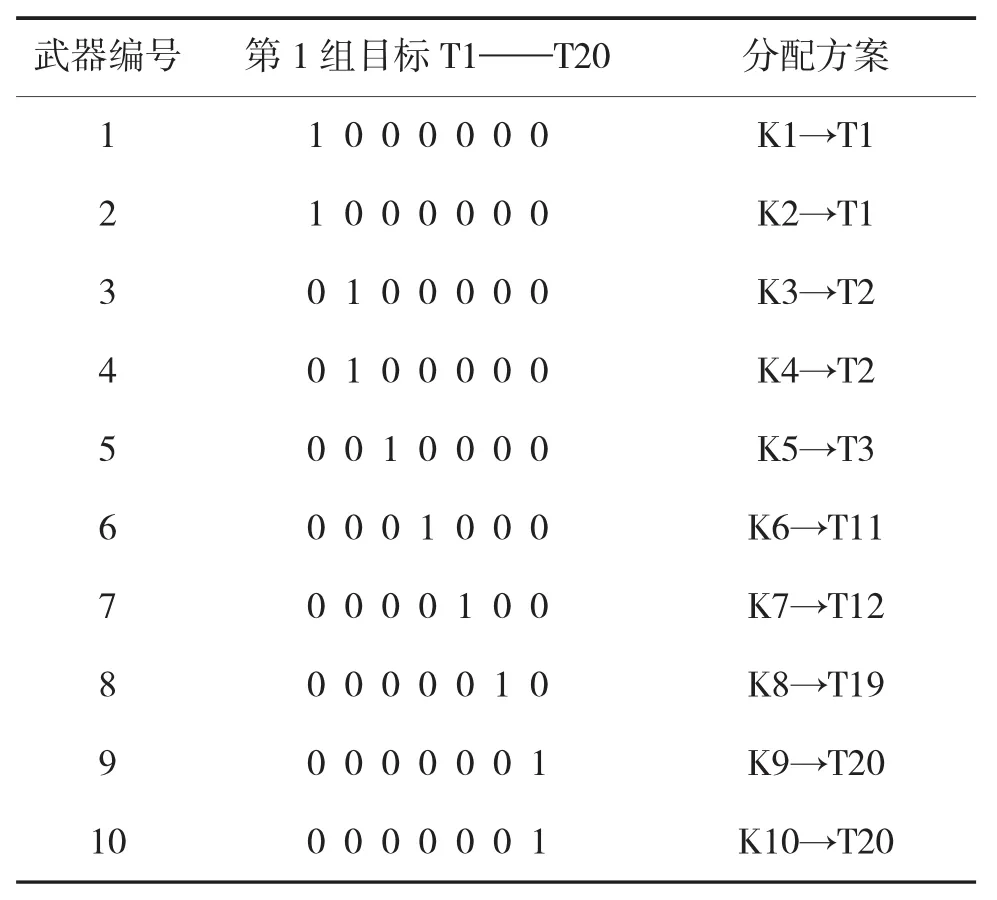
表4 组内分配结果

4 结论

多武器平台协同作战能够极大地发挥单武器平台的作战效能，实现整个分队的协同打击，是未来协同作战的主流模式。在协同过程中，目标分配是协同任务的关键技术。火力协同能够对多个目标进行综合的考虑，从全局的视角进行火力的优化决策，完成火力的分配。

本文从任务目标分配方面进行了研究，基于陆战场的作战环境，构造了整体的作战优势函数，建立了协同作战的任务分配模型，提出一种模糊C均值聚类——拍卖机制的战场目标分配方法。通过仿真实验，表明该任务分配模型能够充分体现协同任务分配的优越性。聚类算法能够对分组个数进行优化，通过模糊聚类使得具有相似战场价值划分到一个分组内，易于后续协同任务的划分。进而利用拍卖算法将这些方案及时分配给各个武器平台，使得战场目标分配效率更高。拍卖算法与模糊C均值聚类算法的结合提高了运算速度，有效地解决目标分配的问题，提高了火力协同的效率。