基于直觉判断矩阵和证据理论的群组决策方法*

王 攀，陈云翔，蔡忠义，张洋铭

（空军工程大学装备管理与安全工程学院，西安 710051）

0 引言

针对复杂的多属性决策问题，为保证决策结果的科学性，一般由多位相关领域专家，根据决策对象的实际情况，结合自身认识，开展群体决策，并形成一致性的决策结果。

由于考虑因素的复杂性和认知判断的局限性，当专家在决策过程中往往无法直接给出明确的决策结果，常需要根据相关准则进行比较权衡，构建判断矩阵，并采用合理的方法计算排序[1]。模糊集理论的提出，为有效处理专家在进行对比分析时存在模糊性和不确定性的问题，提供了解决思路和方法[2-4]。但是，模糊集的表达形式无法描述专家举棋不定时的犹豫状态，显得生硬。直觉模糊集结合隶属度、非隶属度和犹豫度3种信息细化模糊表达，能够更加细腻地展现专家的行为认知，丰富和发展了模糊集，能够更好地处理模糊信息，因而在决策理论的研究中得到重视[5-7]。基于此，采用直觉模糊数描述对比结果，从而构建直觉判断矩阵用于决策分析的方法已有所研究[8-9]。

实际决策中，考虑到不同专家对属性的认知存在差异，为提高决策结果的客观性，本文在属性层面，对专家权重加以区分[2]。目前，类似于利用模糊聚类[10]、TOPSIS[11]、相似度[12]、证据冲突度模型[2，13-14]等以专家个体与群体决策的差异来确定专家权重的方法，存在为获得一致性结果，过分削弱个人与群体决策差异大的专家权重的弊端。在专家对属性的直觉模糊评价值中，犹豫度体现了专家对评价的肯定程度，能够从侧面区分专家权重。

在决策信息集结方面，鉴于证据理论在不确定性的描述、量度和合成方面的明显优势，将证据理论用于直觉模糊信息集结已有广泛研究[13-15]。文献[14]利用直觉模糊对5类偏好信息加以统一并利用证据理论进行合成，文献[15]采用直觉模糊数表示评价信息并转化为Mass函数进行证据合成。文献[14-15]以直觉模糊数构造Mass函数，但都忽略犹豫度的存在。

本文在属性权重已知的情况下，利用直觉模糊数描述不同属性下，不同专家关于各方案的对比分析结果，构建直觉判断矩阵，结合证据理论相关方法，进行方案排序。在专家关于属性的判断描述方面，采用直觉模糊数能够形象地描述专家判断过程，更加符合决策实际。通过直觉判断矩阵一致性转化，确定属性直觉模糊数型权重。针对基于证据冲突度确定专家权重的片面性，利用犹豫度加以修正，保证专家权重的合理性。根据直觉模糊理论和证据理论的相关研究，进行决策信息集结和方案排序，并通过算例验证方法的有效性。

1 相关概念

1.1 直觉模糊集

定义1[5]设X是一个给定的论域，若存在以下映射关系：，使得和，且，满足，则称A为X上的一个直觉模糊集，记为：

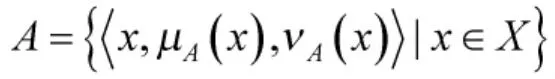
定义2[5]直觉模糊数的得分值和精确值分别记为。

1）若 Sa＞Sb，则 a＞b。

2）若 Sa=Sb，则有：

① 若 Ha＞Hb，则 a＞b；

② 若 Ha=Hb，则 a=b；

③ 若 Ha＜Hb，则 a＜b。

定义3[5]设为直觉模糊集。映射使得

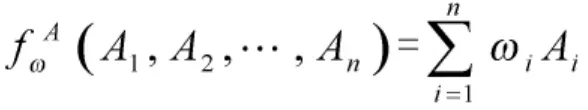
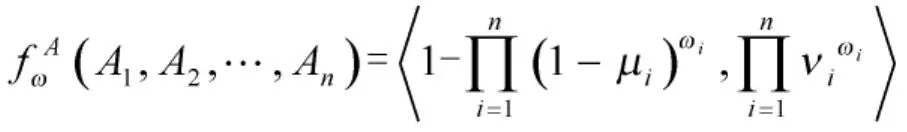
1.2 直觉判断矩阵

定义4[16]对于判断矩阵，其中，。若，，，则称R为直觉判断矩阵。

其中，μij为表示两两比较时对前者的支持程度，vij为表示两两比较时对后者的支持程度，πij为对比时的不确定程度。

1.3 证据理论

定义6[14]设Θ为识别框架，m为识别框架Θ上的Mass函数，，则称由所定义的函数为Θ上的信任函数。

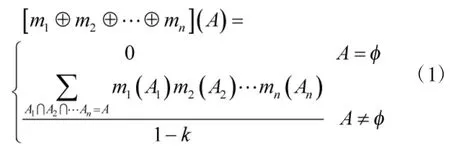
式中，k为冲突系数，且

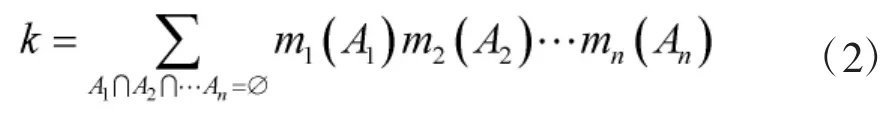
2 问题描述和数据处理

关于属性os，每名专家对方案的优劣程度进行两两比较，且比较结果采用直觉模糊数描述，构建直觉判断矩阵。关于属性os，专家Pk对于不同方案的直觉判断矩阵为：

为保证决策结果的可靠性，进行计算时，判断矩阵必须满足一致性条件，直觉判断矩阵亦是如此。文献[16-17]给出了直觉判断矩阵的加型一致性定义，提出了直觉判断矩阵排序中转法，获得直觉模糊数型权重，并证明了其合理性。

本文根据上述方法，关于属性os，将专家Pk的直觉判断矩阵转化为专家Pk对于方案xi的直觉模糊评价值。其中，

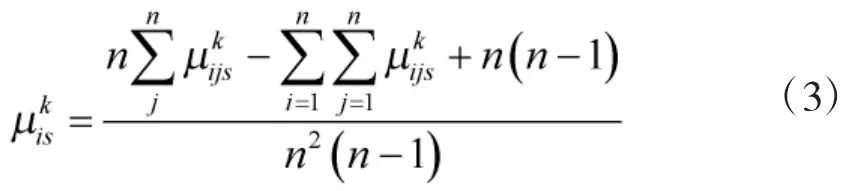
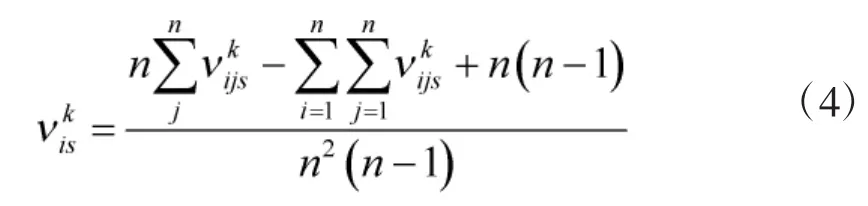
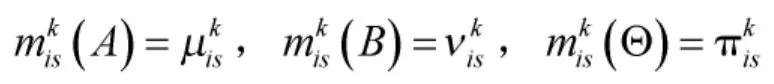
加以整理，构建关于属性os，专家Pk对于方案xi的Mass函数矩阵：

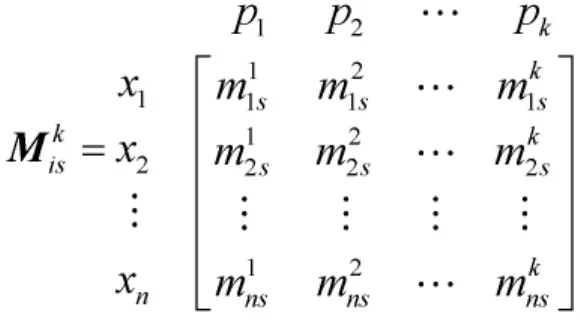
3 专家权重分配

3.1 专家权重分配

本文在构造Mass函数的基础上，利用证据冲突度计算证据信息的冲突程度，确定专家权重。

定义8[18]设识别框架Θ上有两个Mass函数m1和m2，两者之间距离可表示为：

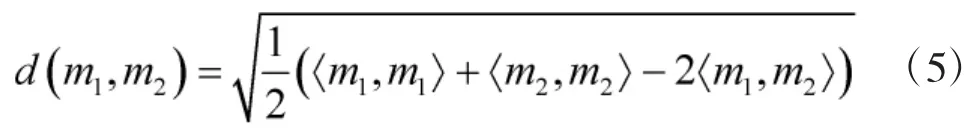
关于属性os，专家Pk与Pl之间对于方案xi进行评价的证据冲突度为：

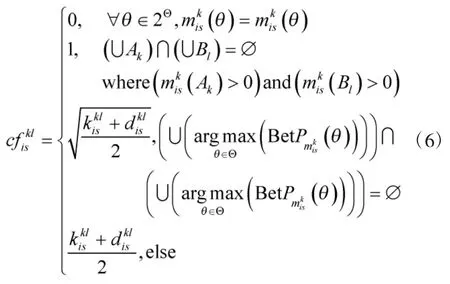
由于方案之间重要程度相同，可以得到关于属性os，专家Pk与Pl之间的证据冲突度为：

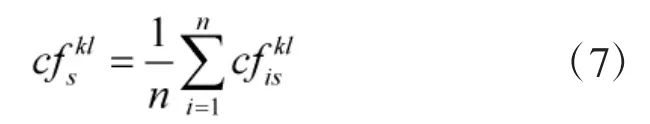
则，关于属性os，专家Pk基于冲突度的权重为：

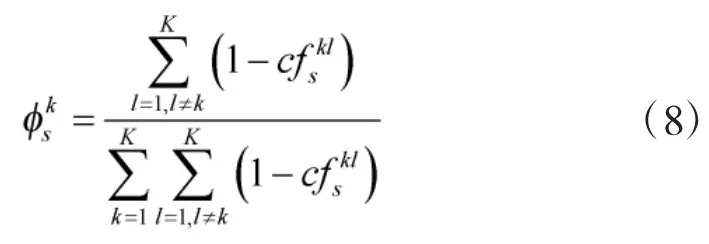
3.2 专家权重修正

基于证据冲突度的专家权重确定方法，其本质还是通过判断专家个体决策结果与群体决策结果之间的偏离程度进行区分，过分削弱综合支持度低的专家权重的弊端依然存在。

针对某一属性，专家在不同方案的对比分析中，所给出的直觉模糊判断值的犹豫度反映了专家对该属性的把握程度。犹豫度小，说明该专家对属性的了解程度高，应赋予较大的权重。文献[19]提出了一种根据非犹豫度进行精确加权的方法，并验证该方法的单调性、尺度不变性和确定专家权重的有效性。

基于此，本文利用关于属性os，专家Pk对于不同方案给出的直觉模糊判断矩阵中的犹豫度，对同种属性下不同专家的权重加以修正，以防止综合支持度低的专家权重过分削弱。

关于属性os，专家Pk基于犹豫度的修正权重为：

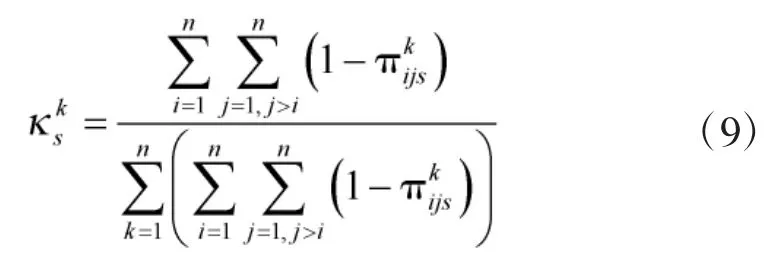
通过线性平均，可获得关于属性os，专家Pk的最终权重为：

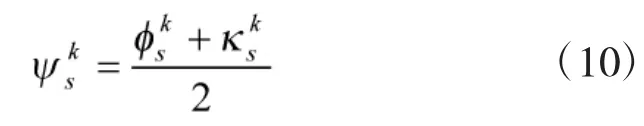
4 决策结果综合

4.1 证据信息修正

为促进证据信息的有效合成，本文采用证据权[9，20-22]对 Mass函数进行修正，确保证据与所含信息的同等地位。

根据证据权相关算法，对Mass函数进行修正：

通过转化，减少证据权小的证据的确定程度，增加不确定性程度，使其与所含信息处于相同地位。

关于属性os，利用证据权修正后专家Pk对于方案xi的Mass函数为：

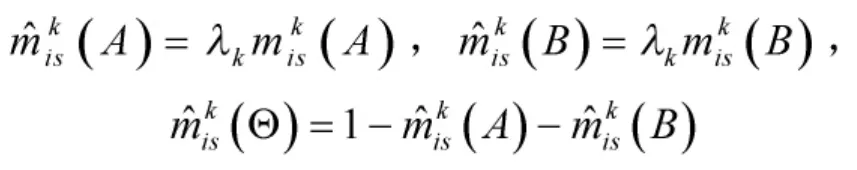
其中，

修正后，关于属性os，专家Pk对于方案xi的Mass函数矩阵为：

4.2 决策信息集结

根据定义6，利用证据合成规则合成关于属性os，所有专家对于方案xi的证据信息，可得各方案的Mass函数向量。其中，

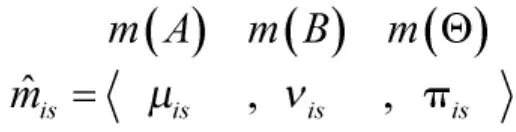
在得到所有属性下，各方案的Mass函数向量后，则可构建方案关于属性的直觉模糊决策矩阵：

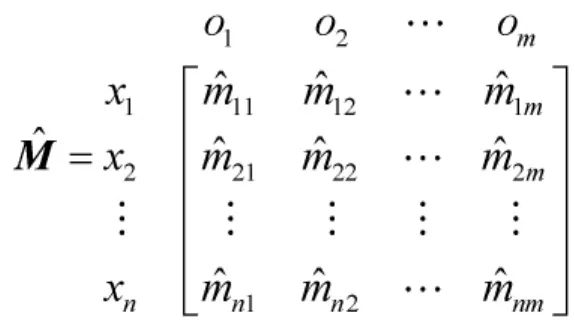
结合属性权重向量ωs，利用加权集结算子集结方案关于不同属性的直觉模糊决策值，可得各方案的直觉模糊决策向量。其中，。且，。

最后，计算每个方案的得分值Si和精确值Hi，进行方案排序。

5 算例分析

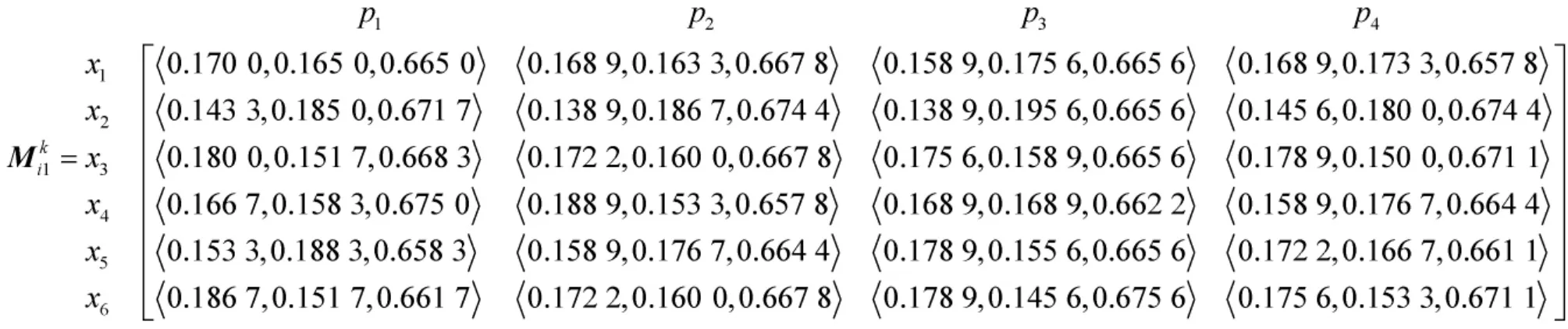
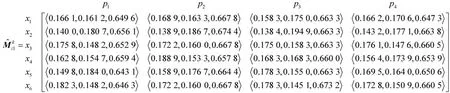
关于属性 o1，根据式（3）、式（4）将 4 位专家所给的直觉判断矩阵转化为直觉模糊评价值，并构建专家Pk对于方案xi的Mass函数矩阵：

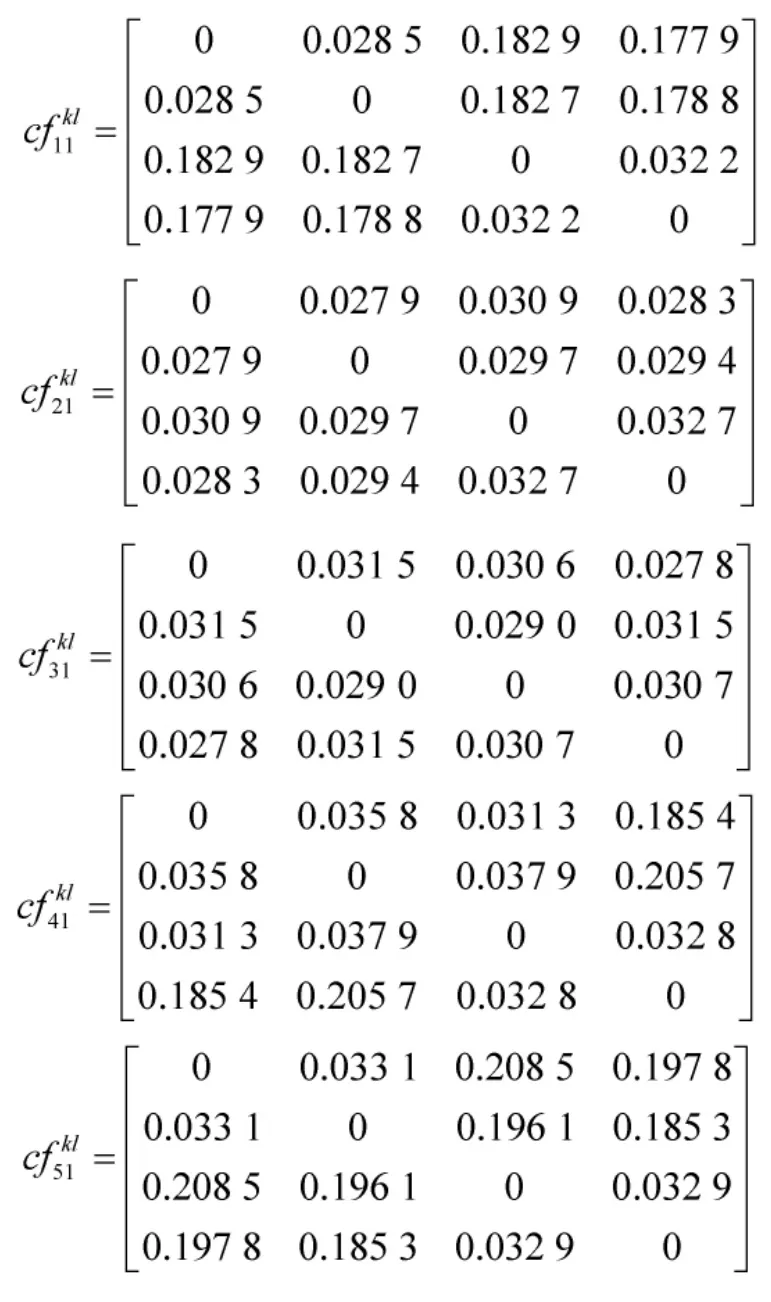
结合式（2）、式（5）、式（6）计算关于属性 o1，专家Pk与Pl对于方案xi的证据冲突度：

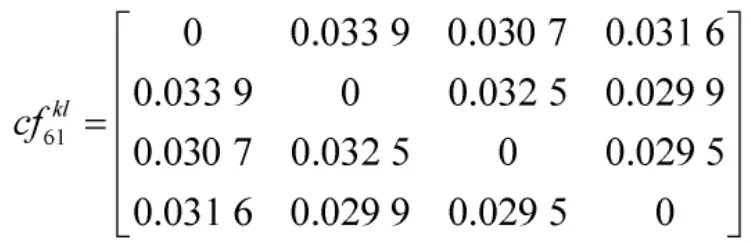
关于属性os，根据式（7）可得专家Pk与Pl之间的证据冲突度为：

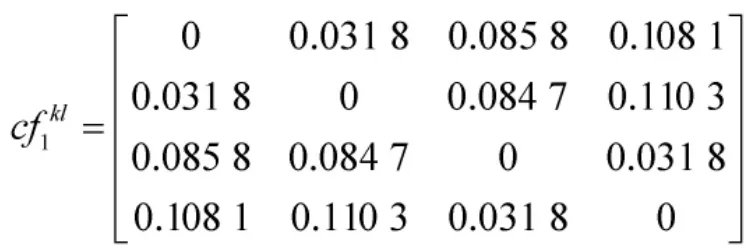
关于属性o1，根据式（8）计算专家Pk基于冲突度的权重向量：

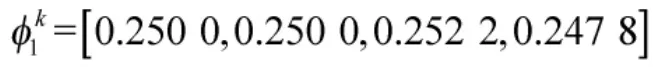
关于属性o1，根据式（9）计算专家Pk基于犹豫度的权重向量：

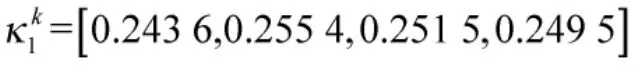
关于属性o1，根据式（10）获得专家Pk的最终权重向量：

关于属性 o1，根据式（13）、式（14）利用证据权修正专家Pk对于方案xi的Mass函数，获得修正后的Mass函数矩阵：

根据式（1）、式（2）利用证据合成规则集结专家对于方案xi的证据信息，得到关于属性o1，不同方案的Mass函数向量为：

同理，关于属性 o2，o3，o4，o5，通过构建直觉判断矩阵，并逐步计算不同方案的Mass函数向量（计算过程略）。则可构建方案关于属性的直觉模糊决策矩阵：

集结方案关于不同属性的直觉模糊决策值，得各方案的直觉模糊决策向量M。

计算各方案的得分值和精确值为：

6 结论

本文针对属性权重已知的群体决策问题，讨论了方案对比分析的描述，专家权重的分配，以及决策信息的集结问题。

1）采用直觉模糊数更加形象地描述专家关于方案的对比分析结果，构建直觉判断矩阵，通过一致性条件转化为直觉模糊评价值，奠定了决策基础。

2）明确了在属性层面区分不同专家的权重，提出了基于证据冲突度和犹豫度的专家权重分配方法。

3）以完整的直觉模糊数结构，构造Mass函数和证据合成计算，更能反映直觉模糊特性。

4）为解决相关问题提供了一种行之有效的理论方法。