分布式MIMO数字阵列雷达多目标定位*

费太勇，谭贤四，巫 勇，王洪林，唐 瑭

（空军预警学院，武汉 430019）

0 引言

多输入多输出（Multiple Input Multiple Output，MIMO）雷达是利用多个发射天线同步地发射分集的波形，同时使用多个接收天线接收回波信号，并集中处理收发信号的一种新型雷达体制[1-2]。其中，分布式MIMO雷达（又称统计MIMO雷达）由于各收发天线的位置相距较“远”而具有良好的空间分集增益、结构增益和极化分集增益[2]。众多学者对分布式MIMO雷达利用空间分集增益和结构增益提高目标定位精度进行了深入的研究[3-8]，然而由于分布式MIMO雷达天线是无方向性的，故目标定位时需要在整个探测空域对目标位置在三维空间进行遍历搜索，由此带来了巨大的搜索计算量。其实分布式MIMO雷达天线也可以采用波束易于灵活控制的数字阵列天线。数字阵列天线指的是接收和发射波束都采用数字波束形成技术的全数字阵列扫描天线[9]，即每个天线都是由若干个阵元组成的相控阵天线。数字阵列天线是相控阵天线发展的趋势，会逐渐成为相控阵天线的主流[10]。数字阵列天线可使分布式MIMO雷达的各个天线获得灵活的波束指向，进而便于各天线波束的联合扫描与探测。文中将这种采用数字阵列天线的分布式MIMO雷达称为分布式MIMO数字阵列雷达。分布式MIMO数字阵列雷达同时保留了相控阵雷达探测波束的方向性和分布式多输入多输出雷达的空间分集增益，以及结构增益在目标定位上的优势。本文将对分布式MIMO数字阵列雷达的多目标定位方法、搜索复杂度和分辨力进行研究，并与常规分布式MIMO雷达和相控阵雷达进行比较分析。

1 MIMO雷达观测模型

图1 MIMO雷达观测模型

设分布式MIMO数字阵列雷达（以下简称MIMO雷达）的观测模型如图1所示，系统在xoy平面内包含L个均匀相控阵子阵，每个子阵的阵元数为M'×N'，每个子阵都是收发共用的。子阵内各阵元间的间距，子阵之间的间距满足空间分集条件[11-12]和短基线（天线间距与目标探测距离相比可忽略不计）条件[13]。子阵内的阵元发射相同波形以获取需要的波束指向，而各个子阵之间发射正交的波形以便于在接收时对各个发射信号所对应的目标回波进行分离。

因为每个子阵都是由M'×N'个阵元组成的平面相控阵，所以子阵的水平波束宽度θ和垂直波束宽度 φ（单位：°）可分别近似为[14]：

如果将L个子阵合成为一个阵元数为M×N的平面相控阵，即LM'N'=MN，则MIMO雷达变为相控阵雷达，此时相控阵雷达的水平波束宽度θ'和垂直波束宽度φ'（单位：°）可分别近似为[14]：

MIMO雷达通过不同子阵波束的联合同步扫描来完成对责任空域的探测。因为MIMO雷达子阵间距满足短基线条件，故探测过程中不同子阵同步扫描时的波束近似重合。

2 MIMO雷达多目标定位方法及其搜索复杂度

2.1 多目标定位方法

最大似然估计[15]是参数估计的常用方法，可用于MIMO雷达的多目标定位。令根据文献[4-5]的结论，β的最大似然估计为

上式的求解需采用数值搜索的方法完成。具体求解过程为：首先计算MIMO雷达的距离、方位角和俯仰角分辨力；然后根据距离、方位角和俯仰角分辨力确定搜索步进（搜索步进一般小于或等于分辨力）；最后对探测波束内的三维空间Ω进行遍历搜索，其中Ω是由探测波束内的目标距离、方位角和俯仰角的所有可能组合构成的三维空间。

2.2 搜索复杂度

假设MIMO雷达的最大探测距离为Rmax，子阵水平波束宽度为θ，垂直波束宽度为φ，在探测波束内的距离、方位角和俯仰角的搜索步进分别为 ΔR、Δθ和 Δφ，则相应的搜索长度分别为和。故MIMO雷达探测波束内的搜索单元数目为。假设式（5）在每个搜索单元的平均运算量为η，则MIMO雷达的搜索复杂度C为

现利用式（6）比较常规分布式MIMO雷达与文中MIMO雷达目标定位时的搜索复杂度。由于常规分布式MIMO雷达天线是全向辐射的，其水平波束宽度相当于360°，垂直波束宽度相当于90°，故其方位角搜索长度为，俯仰角搜索长度为。在其他条件相等的情况下，文中MIMO雷达与常规分布式MIMO雷达的搜索复杂度之比为。例如，当文中MIMO雷达各子阵的水平波束宽度和垂直波束宽度都为5°时，其目标定位时的搜索复杂度只有常规分布式MIMO雷达的1/1 296。这是因为文中MIMO各子阵的方向性缩短了搜索空域的范围。

3 MIMO雷达目标分辨力

3.1 MIMO雷达模糊函数

模糊函数[16]常用来分析雷达信号的模糊度和分辨力。下面将利用单基地雷达模糊函数的思想推导MIMO雷达的模糊函数，并以此来分析MIMO雷达的距离、方位角和俯仰角分辨力。

假设：MIMO雷达探测波束内有两个目标 p1、p2，极坐标分别为和在信道中的回波时延分别为，时延差为。则信道lk的模糊函数[16]可写成

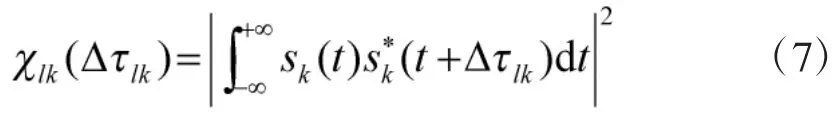
式（7）仅可表示信道lk对不同时延目标的分辨能力。而MIMO雷达是将各信道的输出进行求和累加来进行目标检测和定位的[11]，故其对目标的分辨能力应由所有信道共同决定，所以MIMO雷达模糊函数可定义为所有信道模糊函数的求和取平均，即

式（8）可表示所有信道对目标的综合分辨能力。由式（4）可知，在子阵位置一定的情况下完全由和决定，故式（8）可进一步写成

3.2 仿真分析

MIMO雷达的距离、方位角和俯仰角联合模糊函数难以作图表示。为了便于仿真分析，首先假设距离不变，分析MIMO雷达的方位角和俯仰角模糊函数；然后再假设MIMO雷达的俯仰角不变，分析MIMO雷达的距离和方位角模糊函数。

3.2.1 MIMO雷达方位角、俯仰角分辨力

图2 MIMO雷达俯仰角、方位角模糊图

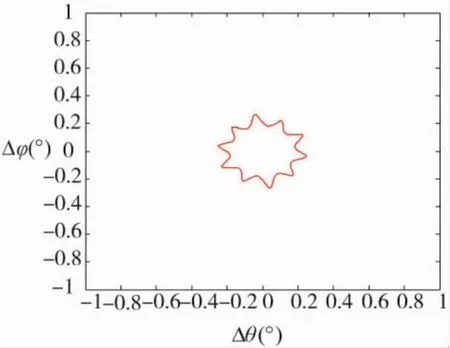
图3 MIMO雷达俯仰角、方位角-6 dB等高线图

从图2、图3可以看出，虽然MIMO雷达子阵的方位角和俯仰角波束宽度都为5°，但子阵分置导致的结构增益可大大提高其方位角和俯仰角的分辨力，图3中MIMO雷达的方位角和俯仰角分辨力约为 0.25°，从等高线中心（0，0）到等高线的最远距离也不超过0.3°。相比较相控阵雷达2°的方位角分辨力和2.5°的俯仰角分辨力，MIMO雷达角分辨力提高了约10倍。值得注意的是相控阵雷达采用的是波束增益最大值的-3 dB分辨力，而MIMO雷达采用的是模糊图最大值的-6 dB分辨力，故实际中MIMO雷达的分辨力优势较相控阵雷达可能更为明显。

3.2.2 MIMO雷达的距离、方位角分辨力

假设某MIMO雷达需要在方位角为（-60°～60°）的扇区内对弹道导弹进行远程预警且L=3，M'=20，N'=20，通过优化布站[17]可使子阵之间的间距满足空间分集条件和短基线条件，优化布站后子阵极坐标分别为（150 km，π/2，0）、（0，0，0）和（150 km，3π/2，0），信号形式同前。

如果将MIMO雷达的L×M'×N'=1 200个阵元合成为一个30×40的平面相控阵，则MIMO雷达变为相控阵雷达。相控阵雷达的距离分辨力约为c/2B=150 m，方位分辨力约为 3.3 °[9，19]。根据式（10），MIMO 雷达在（3 000 km，45°，0°）处的距离、方位角模糊图如图4所示，相应的-6 dB等高线图如下页图5所示。

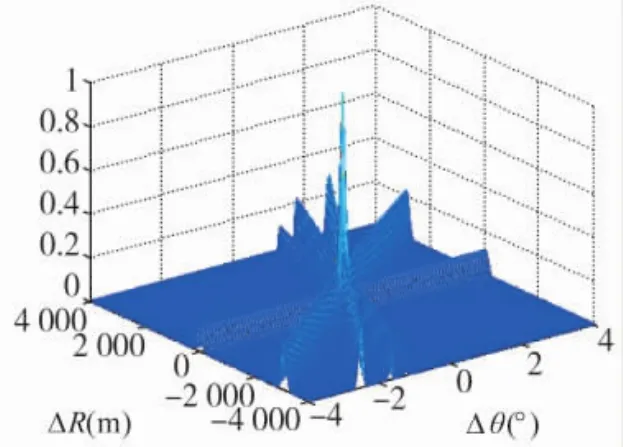
图4 MIMO雷达距离、方位角模糊图

从图4、图5可以看出，MIMO雷达的距离分辨力约为260 m，方位分辨力约为0.26°。相比较相控阵雷达，MIMO雷达的距离分辨力稍有下降，但方位角分辨力却大大提升了。在3 000 km的探测距离上，相控阵雷达3.3°方位分辨角对应的分辨弧长为172 787 m；MIMO雷达0.26°方位分辨角对应的分辨弧长为13 613 m。故与方位角分辨力的改善相比，MIMO雷达距离分辨力的降低（从150 m变为260 m）是可以忍受的。

图5 MIMO雷达距离、方位角-6 dB等高线图

虽然MIMO雷达在距离分辨力下降很小的情况下，大幅提升了方位分辨力，但MIMO雷达存在狭长的距离、方位角模糊带，如图5所示。当两个目标的位置关系位于图5所示的模糊带中，MIMO雷达是难以分辨出来的。由于常规MIMO雷达天线无方向性，故存在很长的距离、方位角模糊带。而文中的MIMO雷达子阵的波束是有方向性的，水平波束宽度为5°，故其距离、方位角模糊带的方位角范围仅为5°，进而大大降低了距离、方位角模糊带的长度。如果减小MIMO雷达子阵水平波束宽度，还可以进一步降低距离、方位角模糊带的长度。不过，MIMO雷达子阵波束宽度过窄不利于联合同步扫描时的波束重合。故MIMO雷达子阵波束宽度的确定需要综合上述两种因素进行折中考虑。

5 结论

本文研究了分布式MIMO数字阵列雷达的多目标定位问题。研究结果表明：分布式MIMO数字阵列雷达由于子阵波束的方向性，在目标定位时不需要像常规分布式MIMO雷达那样，在整个探测空域进行三维空间的遍历搜索，只需要对子阵波束内的三维空间进行遍历搜索即可，进而大大降低了目标定位时的搜索复杂度；常规分布式MIMO雷达天线广域分置带来的结构增益，可以很好地提高目标的角分辨力，但会带来很长的距离-角度联合模糊带，而分布式MIMO数字阵列雷达子阵波束的方向性可大大缩短模糊带的长度。研究结果对分布式MIMO雷达的系统设计、天线配置和实际应用等研究具有重要的参考价值。