复合材料圆管阻尼特性研究
2019-04-22白宇杰王黎明张小章
白宇杰,王黎明,张小章
(1.核工业理化工程研究院,天津 300180;2.清华大学 工程物理系,北京 100084)
目前碳纤维复合材料由于比强度高、比刚度高和可设计性等优异性能,已广泛应用于各工业领域,如纤维缠绕成型的复合材料圆管在高速旋转机械上的应用[1]。复合材料阻尼对于碳纤维的应用有着重要影响,需在设计中予以考虑。Jean-Marie等[2-5]从2002年开始针对复合材料单向铺层板阻尼特性的理论计算和试验研究做了系统性的工作,梳理总结了前人的计算方法,并提出了修改验证。Treviso等[6]对复合材料在阻尼领域的知识进行了详细综述。任勇生等[7-8]对阻尼研究进行了总结,并采用变分渐进法对复合材料悬臂梁的阻尼特性进行了计算。由众多文献可发现,关于复合材料圆管的阻尼分析相对较少。Alam等[9]在动力学研究的基础上用变分方法研究了径向简支复合材料圆柱壳的阻尼特性。Hufenbach等[10]用能量Ritz法分析了简支复合材料圆柱壳的阻尼特性。
复合材料圆管既可视为梁,也可视为壳。通过在Timoshenko梁模型中引入复模量[11-12]就可对复合材料圆管的阻尼特性进行分析。运用经典壳理论可得到梁模型中采用的纵向和面内剪切等效模量。为了计算阻尼,材料参数考虑使用复数形式的模量,实部代表存储,虚部代表耗散。求解Timoshenko梁理论可同时得到模态频率和模态损耗因子。Singh等[13]讨论了使用梁理论的限制条件。本文将波动法引入Timoshenko梁理论微分方程中进行求解,可方便地得到各种边界条件下的阻尼结果。将复合材料圆管视为壳进行动力学研究已较为成熟,Lam等[14-16]对比分析了不同壳理论并研究了边界条件、铺层制度等对复合材料圆管振动特性的影响。波动法是进行复合材料圆管振动研究的一种较高效的方法,本文将该方法用在Love一阶壳理论中并用模态应变能法得到其阻尼特性。
本文采用复模量方法的Timoshenko梁理论和模态应变能法的Love一阶壳理论建立复合材料圆柱壳动力学方程,在振动分析的结果上建立结构阻尼模型并进行阻尼特性分析,对复合材料圆管进行模态试验,并与理论计算结果进行对比。
1 Timoshenko梁模型
本文采用的Timoshenko梁理论最早由Tsai等[17]提出,其中包括纵向和面内剪切等效模量。
(1)
G=U5-U3γ
(2)
其中:E为弯曲模量;G为剪切模量;Ui(i=1~5)为铺层常量;γ和β为铺层常数。
该模型假设圆管轴线与材料对称轴一致,确保不同方向应力分量没有耦合。为得到材料阻尼,所有铺层常量Ui为复数,因此等效模量也是复数。求解包括剪切效应和转动惯量的Timoshenko方程为:
(3)
其中:I为转动惯量,I=πR3t(1+t2/4R2),R为圆管半径,t为圆管壁厚;ρ为密度;A为截面积;k=1/2,为剪切修正系数;r为整个长度方向上的形变。
代入rn(z,t)=Rneiknzeiωnnt进行求解:
(4)
其中:kn为边界条件系数,根据梁理论得到;ωnn为各阶模态复频率;n为环向波数。该多项式方程有两对互相共轭的复数根,其中模相对小的是长度方向上的弯振模态,实部和虚部分别为:
(5)

2 Love一阶壳理论
采用Love一阶壳理论进行阻尼特性分析包括两个步骤:1) 求解得到模态振型;2) 在模态振型的基础上采用应变能法得到损耗能量,继而得到模态损耗因子。对于如图1所示铺层圆柱壳,厚度为h,半径为R,长度为L。采用坐标系Oxθz描述圆柱壳系统,u、v与w分别为圆柱壳在x、θ与z方向上的位移。基于Love一阶壳理论,采用Hamilton原理建立的动力学方程[8]如下:
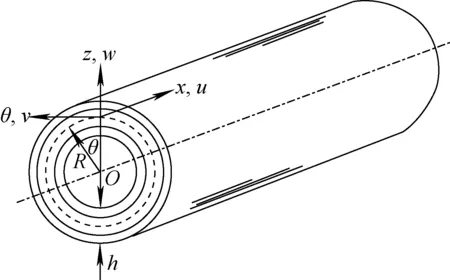
图1 复合材料铺层圆管模型Fig.1 Model of composite laminated cylindrical tube
(6)
其中,Lij(i,j=1,2,3)为微分算子。壳体的振型函数可表示为波动的形式:
u=Umne-ikmxcos(nθ)eiωt
v=Vmne-ikmxsin(nθ)eiωt
w=Wmne-ikmxcos(nθ)eiωt
(7)
其中:Umn、Vmn、Wmn分别为3个坐标方向上的波幅;ω为角频率;km为轴向波数。
将式(7)代入式(6),根据存在非零解的条件得到关于圆柱壳轴向波数、环向波数和频率的特征方程:
f(km,n,ω)=0
(8)
利用该方程就可得到复合材料圆管的模态频率,其中关键一步就是根据壳体的边界条件选取相同边界条件下梁的波数作为壳体的轴向波数[7],根据所分析振型选取环向波数,得到模态频率后,即可得到相应的振型函数,如式(7)所示,振型函数是计算应变能的基础。本文主要讨论一阶弯曲振动的阻尼特性。
图2示出复合材料铺层圆管的截面模型。对于图2所示的铺层结构的圆柱壳模型,假设各层复合材料是正交各向异性,则第k层的应变能[5]为:
(9)
其中:σk为各层主轴应力;εk为各层主轴应变;hk为各层厚度。

图2 复合材料铺层圆管截面Fig.2 Cross-section of composite laminated cylindrical tube
根据材料本构关系替换主应力为主应变,然后用偏轴应变替换主轴应变,接着将参考面应变和曲率代入偏轴应变中,令:
则得到各振动方向应变能为:
(10)
其中:Q为主轴刚度矩阵;l为cosθ,θ为铺层角度;m为sinθ。
将振型函数(式(7))代入偏轴应变中计算得到应变能,得到第k层的应变能为:
(11)
于是得到第k层由于阻尼耗散的能量为:
(12)
其中:η11、η22分别为纤维纵向和横向上的拉压阻尼损耗因子;η12为面内耦合损耗因子;η66为面内剪切损耗因子。进一步可求得整体的模态损耗因子为:
η=∑ΔUk/∑Uk
(13)
3 试验测试
试验系统如图3所示。复合材料圆管水平悬挂在空中,如此得到自由边界条件。圆管表面划分为网格以方便锤击测量。力锤用来敲击网格节点,粘贴在圆管上的加速度传感器用来测量振动信号。加速度传感器约为0.4g,对圆管质量改变很少,不会影响模态测量结果。敲击和振动信号通过调理后在计算机中进行处理测量。
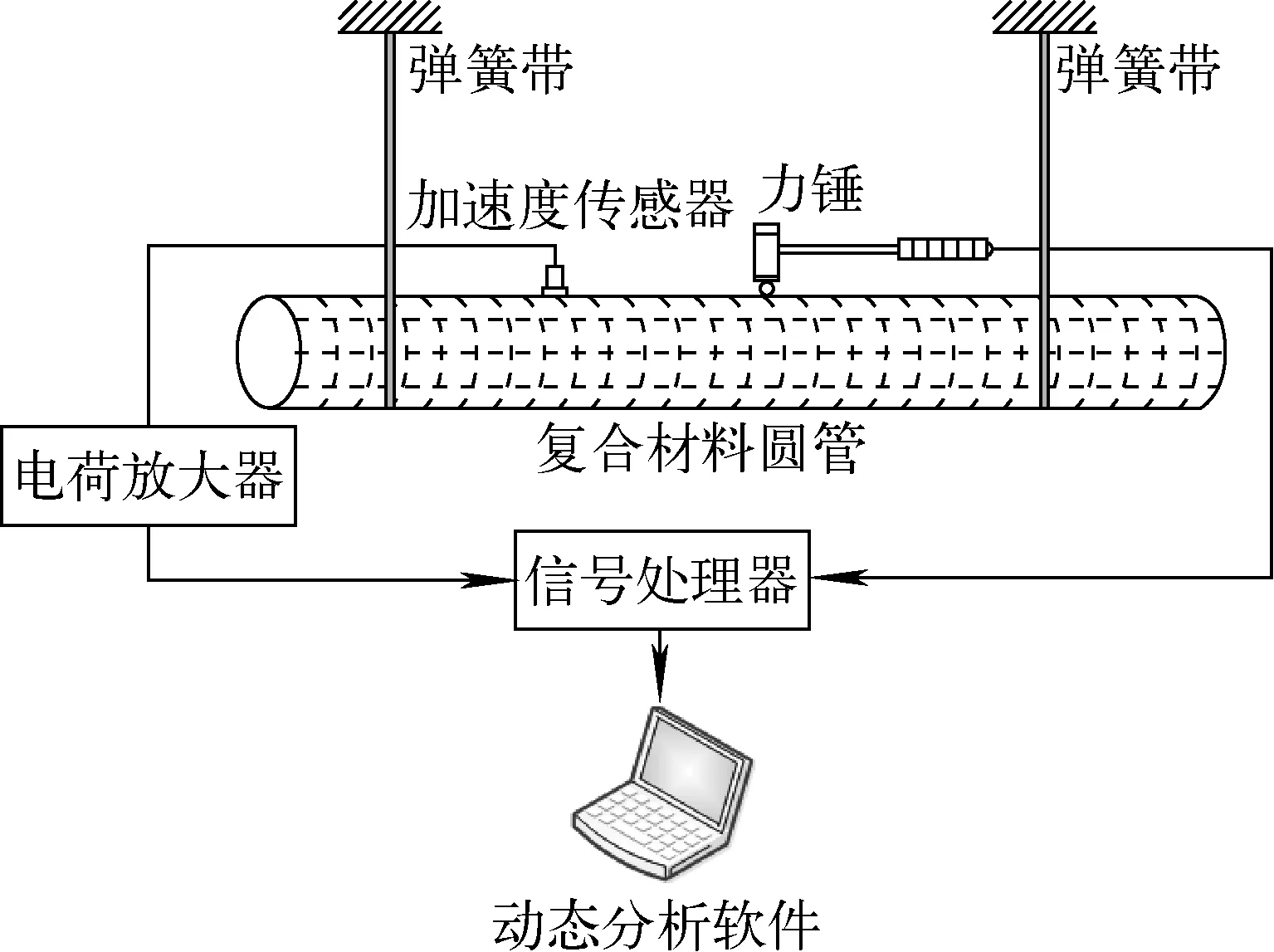
图3 试验测试系统Fig.3 Hammer test system
试验中用到了两个试验件,其长度为2 000 mm、内径为70 mm、壁厚为2 mm,铺层分别是沿轴向90°(即环向)和70°缠绕。根据基本的力学性能测量,可得到材料的基本参数为密度ρ=1 620 kg/m3、轴向模量EL=175.9 GPa、横向模量ET=8.2 GPa、剪切模量G=5.8 GPa、泊松比ν=0.3,复合材料在各方向上的模态损耗因子为η11=0.4、η22=2、η66=2.89。
4 结果分析
为检验本文建立的阻尼模型及其近似计算方法的正确性,表1列出3种铺层制度,即沿轴向的铺层制度为[0]16、[90]16和[45/-45]8的复合材料圆管的一弯模态频率和阻尼,并与文献[18]中的有限元结果进行对比分析。由表1可看出,本文结果与文献结果符合得很好。表2、3列出试验与计算结果的对比,包括弯振模态和壳频模态。由表2、3可见:对于弯振损耗因子,壳理论结果和试验结果符合得很好,梁理论误差较大;对于壳频损耗因子,壳理论结果在某些模态上误差较大,梁理论则无法计算壳频模态。
图4示出复合材料圆管的一弯模态损耗因 子随长径比L/d、边界条件和铺层角度、厚径比t/d与环向波数的变化。图4b中,S-S代表双边简支边界,C-F代表悬臂边界,C-C代表双边固支边界。从图4a可看出,在L/d>10时,梁理论和壳理论的计算结果趋于一致,并达到恒定值0.65,考虑到铺层为沿轴向0°,则该恒定值是沿纤维方向的材料损耗因子。由此可知L/d>10时一弯振型中轴向拉压振动贡献了最大的应变能和阻尼损耗,而梁理论仅能计算轴向振动,于是就可得到较为准确的结果。在L/d<10时,梁理论与壳理论计算结果差异较大,壳理论计算值显著高于梁理论的,说明一弯振型中非轴向拉压振动贡献的应变能和阻尼损耗逐渐增大,此时梁理论不再适用。由图4b可知,与壳理论相比,梁理论不能反映边界条件对阻尼特性的影响,对于铺层角度的计算结果也比较粗略。边界条件会影响一弯振型,进而影响应变能大小和阻尼损耗,从图4b可见,在铺层角度<30°和>75°时,双边固支的模态损耗因子最大,在30°~75°之间时,悬臂的最大。由于垂直纤维和剪切方向的材料损耗因子较大,所以在铺层0°时模态损耗因子较大主要来自剪切损耗,在50°~90°时模态损耗因子较大主要因为此时轴向振动方向越来越接近垂直纤维方向。非常有趣的是,3种边界条件在30°处的计算结果一致。由图4c可看出,在计算范围内,t/d对模态损耗因子影响较小,说明一弯模态中沿厚度方向的振动损耗可忽略不计。图4d是前三阶弯振的模态损耗因子随环向波数的变化,在环向波数为1时,一阶、二阶和三阶弯振的模态损耗因子逐步增大,随环向波数增大三者振型模态损耗因子逐渐趋于一致,该模态损耗因子为材料横向损耗因子,说明环形波数较大时环向振动产生的应变能和损耗为主要部分。

表1 梁理论和壳理论的结果验证Table 1 Verification result of beam and shell theories
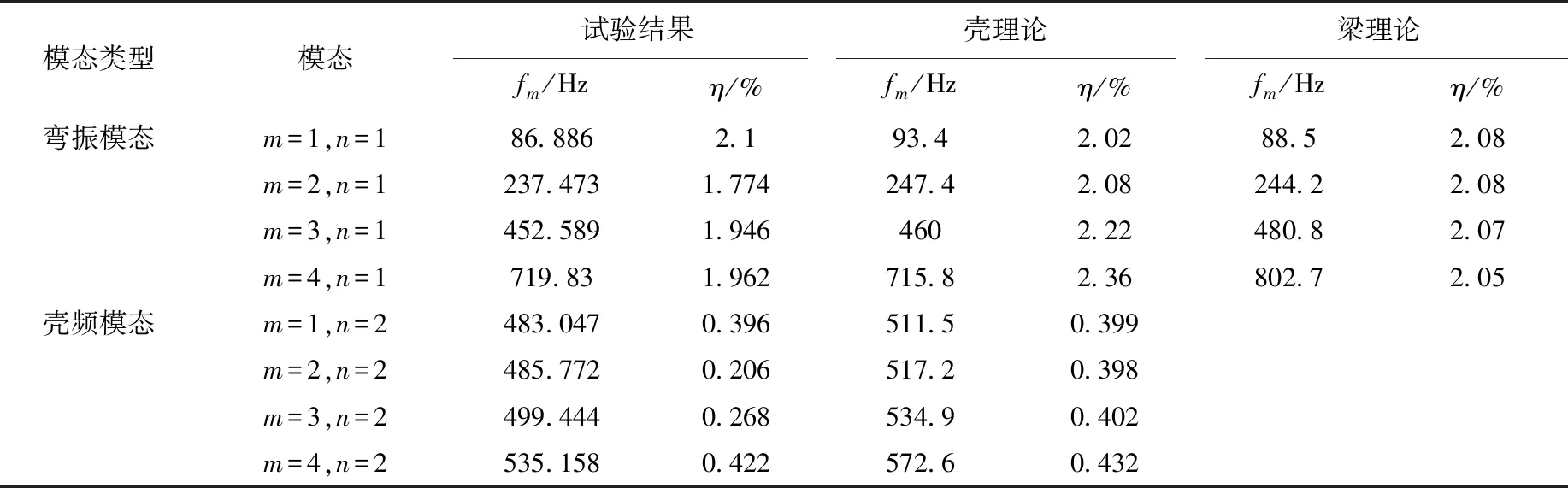
表2 理论结果与90°铺层试验件试验结果对比Table 2 Comparison of theoretical and test results of 90° tube sample

表3 理论结果与70°铺层试验件试验结果对比Table 3 Comparison of theoretical and test results of 70° tube sample
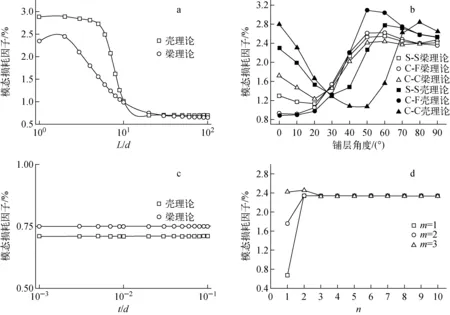
图4 不同几何条件、边界条件和环向波数对模态损耗因子的影响Fig.4 Influence of different aspect ratios, boundary conditions and circumferential numbers on modal loss factor
5 结论
本文采用复模量方法的Timoshenko梁理论和模态应变能法的Love一阶壳理论得到复合材料圆管的阻尼特性,开展了复合材料圆管的模态试验,并与理论计算结果进行了对比分析。最终分析了铺层角度、几何尺寸、边界条件及环向波数对复合材料圆管阻尼特性的影响规律,所得结果如下。
1) 壳理论模型能准确分析复合材料圆柱壳的阻尼性能,梁理论模型仅在轴向振动损耗占优的情况下计算比较准确,如L/d>10时。
2) 一弯模态损耗因子随L/d的增大而减小,在L/d>10时趋于定值。t/d对一弯模态损耗因子影响较小。
3) 一弯模态损耗因子随铺层角度先减小再增大后轻微减小;在铺层角度<30°和>75°时,双边固支的模态损耗因子最大,在30°~75°之间时,悬臂的最大。
