闭合酸蚀裂缝导流能力模拟研究
2019-04-22赵立强缪尉杰罗志锋龚云蕾李屹洋
赵立强,缪尉杰,罗志锋,龚云蕾,汪 鹏,李屹洋
(1.西南石油大学油气藏地质及开发工程国家重点实验室,四川成都610500;2.中海石油湛江分公司,广东湛江524057;3.中国石油新疆油田公司第一采油厂,新疆克拉玛依834000;4.中国石油新疆油田公司重油开发公司,新疆克拉玛依834000)
酸压已成为低渗透碳酸盐岩油气藏实现增产改造的重要措施。酸压改造成功的关键在于酸蚀裂缝趋于闭合后仍具有一定导流能力的裂缝。影响酸蚀裂缝导流能力的主要因素有:岩石类型、地层基质渗透率、地层基质孔隙度、酸液滤失情况、酸液类型及浓度、注酸排量、注酸时间、闭合压力等[1]。目前,对酸蚀裂缝导流能力的实验方法、计算模型较多,但针对闭合酸蚀裂缝导流能力的计算模型及相关模拟却十分少见。
裂缝的宽度和渗透率决定其导流能力,而酸蚀裂缝壁面几何形态符合分形特征[2],利用分形理论可以对酸蚀裂缝壁面的几何形态进行更加准确的描述。该理论最早应用于裂缝表面酸—岩反应模型的研究[2],随后应用于地层中酸液滤失情况的研究[3],识别地层中的裂缝[4]及对地层中裂缝宽度的变化情况进行描述[5]等方面。在表征渗透率上,Dong[7]提出了针对碳酸盐岩储层中天然裂缝的酸化模型;Sarkar[8]等用斯托克斯方程对平行板裂缝中流体的流动状态进行了模拟计算;Coakley[8]等将不规则的裂缝内流体流动状态进行了模拟计算,并求出了裂缝的等效渗透率;A D Hill[9]等提出了一个考虑酸蚀蚓孔影响的滤失模型。酸蚀裂缝闭合模型最早是由Gangi[1]提出的“钉床”模型;Hopkins[1]改进锥体“钉床”并计算缝宽方向上的变形量;J Deng等[1][10]对Myer模型[11]进行了改进,用多个椭圆来表征裂缝中未闭合的区域。在计算导流能力方面,Tsang和Witherspoon[1][12][13]模型、Gong[12][13]模型、JianyeMou[12][13]模型、J Deng[10]模型都能应用于酸蚀裂缝导流能力的模拟计算。
在前人的研究基础上,利用优化分形插值方法来建立粗糙裂缝壁面,求解酸压模型,针对缝宽特征描述对Myer模型进行改进,计算出闭合酸蚀裂缝导流能力,通过正交分析,对各影响因素影响程度大小进行了排序。
1 分形裂缝的建立
1.1 粗糙壁面的生成
用改进自仿射分形插值[14],进行局部邻域划分和选择合适的压缩比,就能插出比较精确的粗糙裂缝壁面。运用地质统计学中的变差函数理论[15],划分局部邻域,实验变差函数的计算公式为:
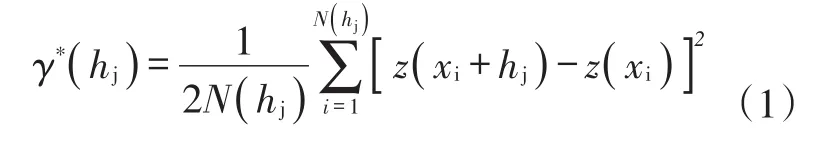
式中:γ*(hj)为实验变差函数;z(xi)为在点xi处的裂缝粗糙壁面高度,m;hj为两观测点间的距离,m;N(hj)为间隔为hj的数据对数目。
将计算出的实验变差函数值,在h~γ*(hj)坐标系中描出散点,再用最小二乘法理论拟合变差函数曲线从而求得变程a=a1,块金值c0=c1,基台值c,总基台值c2=c0+c。取a1为局部矩形邻域的边长,进行局部邻域的划分。
则压缩比sn,m为:
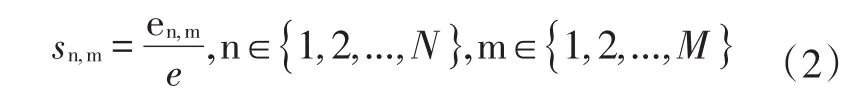
采用改进自仿射分形插值理论数值生成长100 m、高30 m、分形维数2.5、标准偏差0.000 016 m的粗糙分形裂缝壁面(图1)。
1.2 分形裂缝生成
在分形维数2.5、标准偏差0.000 016 m的条件下数值生成的两个粗糙裂缝壁面进行合成,形成一条具有一定宽度的裂缝,该裂缝平均缝宽为0.003 6 m,最大缝宽为0.007 4 m(图2)。
2 分形裂缝酸压模型
为模拟酸压对裂缝几何形态的影响,基于碳酸盐岩储层的裂缝酸压物理模型,根据酸液质量守恒、酸液传质平衡和裂缝宽度变化方程建立了分形裂缝的酸压模型。
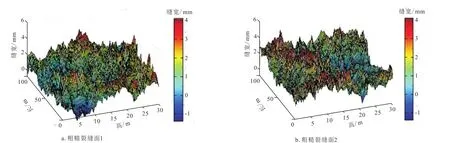
图1 数值生成的粗糙裂缝壁面Fig.1 Rough fracture wall generated by numerical value
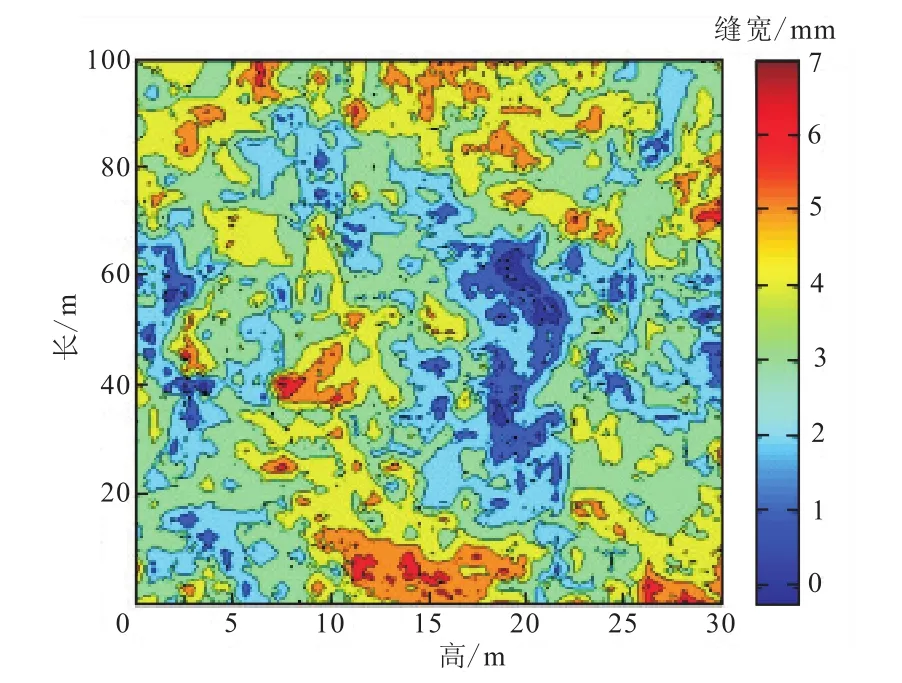
图2 合成的分形裂缝宽度分布Fig.2 Width distribution of synthetic fractal fractures
2.1 假设条件数学模型的建立
为简化计算过程,建立的方程需满足以下假设条件:
1)酸液是不可压缩的,密度恒定;
2)酸液在裂缝中的流型为层流;
3)模拟过程中不考虑蚓孔对酸液滤失的影响;
4)酸—岩反应速度受传质控制。
2.2 数学模型的建立
在假设条件下,把酸化前裂缝壁面的酸液浓度视为0,得到酸液传质平衡方程为:(3)
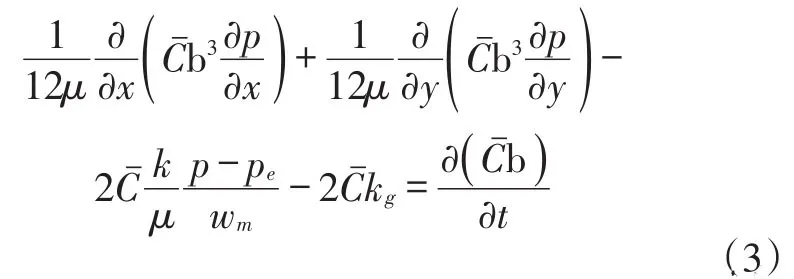
式中:μ为酸液黏度mPa·s;b为裂缝宽度,m;k为岩心基质渗透率,10-3μm2;p为点(x,y)处的压力,MPa;pe为地层压力,MPa;wm为滤失酸液的穿透深度,m;Cˉ为裂缝内点(x,y,z)处的平均酸液浓度,kg/m3。
在单位时间内,酸—岩反应引起的单元体的体积变化量等于溶解的岩石体积,可得裂缝宽度变化方程为:
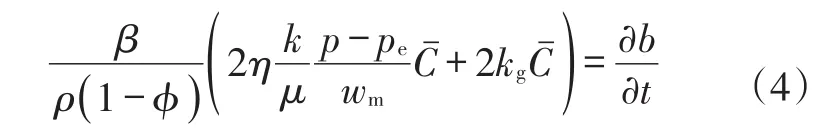
式中:η为滤失酸液中与缝壁岩石发生反应的酸液占滤失酸液的百分数,小数,大多数情况下η≅0;β为酸液的质量溶解能力,表示被溶解的岩石质量与反应的酸液质量之比,kg(岩石)/kg(酸);ρ为岩石密度,kg/m3;φ为岩石孔隙度,小数。
2.3 模型求解
酸压前裂缝内各点的酸液浓度为0,已知分形裂缝宽度及粗糙度数据,从裂缝入口端(即y=0处)向裂缝和基质岩石注入酸液。在酸压过程中,注酸排量恒定,裂缝顶部和底部(即x=0和x=l处)无酸液流动,裂缝出口端(即y=h处)的压力为地层压力,裂缝入口端的酸液浓度为C0。式(5)和式(6)分别为分形裂缝酸压数学模型的初始条件和边界条件。
初始条件:
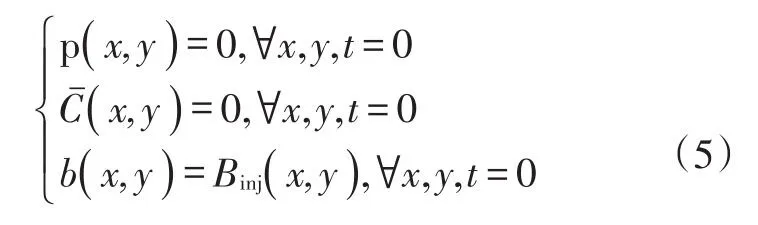
式中:Binj(x,y)为分形裂缝的初始宽度分布,m。
边界条件:
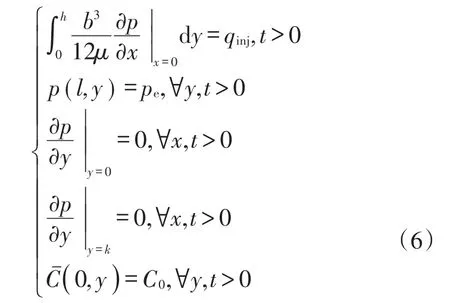
式中:qinj(x,y)为注酸排量,m3/min。
在已知初始裂缝宽度b和酸液流量恒定的情况下,对式(3)和式(4)修正,以压力p和酸液浓度C为初始迭代计算步,运用Gauss—Seidel方法[16]进行求解。按照表1所示参数进行模拟得到如图3所示的分形裂缝酸压模拟结果。分形裂缝酸压前的平均缝宽如图2所示,为0.003 6 m,最大缝宽为0.007 4 m;分形裂缝酸压后的平均缝宽如图3所示,为0.005 4 m,最大缝宽为0.011 8 m。
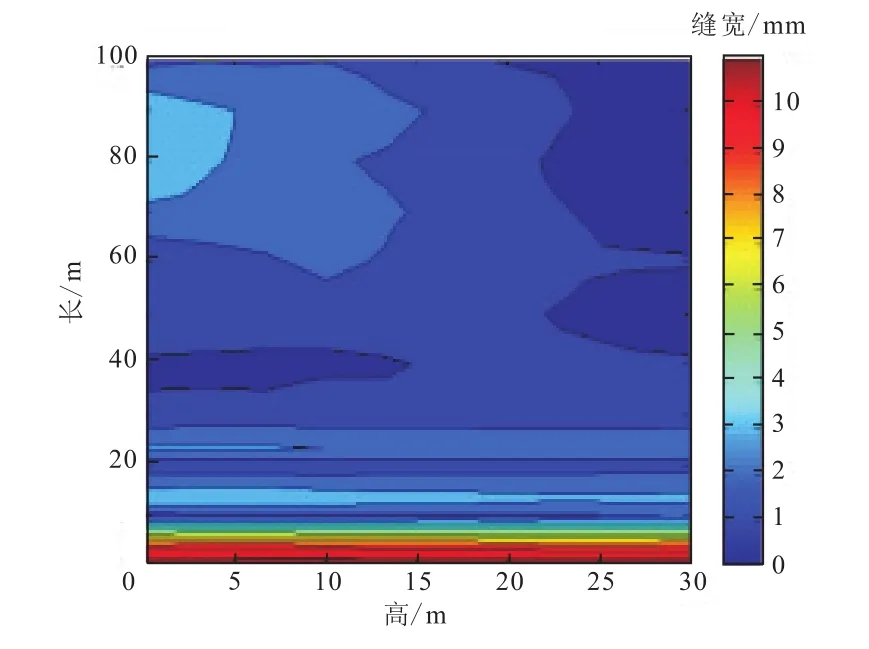
图3 分形裂缝酸压模拟结果Fig.3 Fractal fracture acidification simulation results
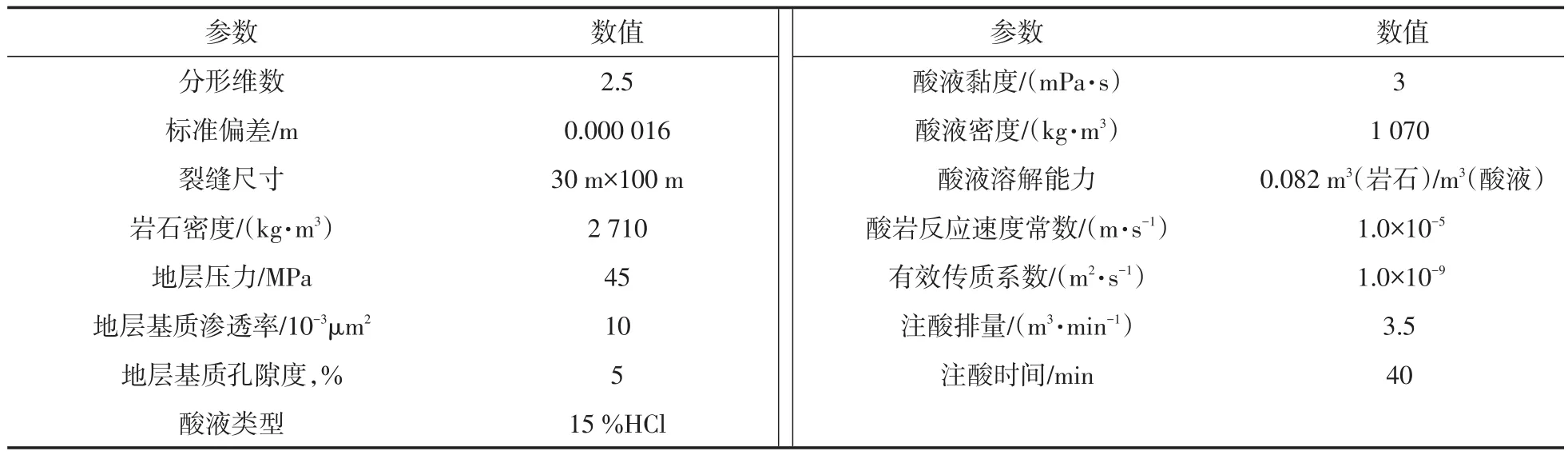
表1 裂缝酸压参数Table1 Parameters of acidification of fracture
3 酸蚀裂缝闭合模型
在闭合压力的作用下,酸蚀裂缝会逐渐闭合,裂缝壁面上的粗糙颗粒相互接触后会发生变形。在模拟过程中,沿裂缝长度方向将裂缝分为若干剖面,分别对每个剖面在闭合压力作用下的闭合特征进行研究。利用若干椭圆的Myer模型替代Airy应力函数和复变函数理论[1],对椭圆的变形情况进行分析计算,对各裂缝剖面的闭合特征进行描述。
Myer推导了计算多个椭圆闭合量的解析解的求解方法[1]。他用多个椭圆表征未闭合的裂纹,并对裂纹的闭合特征进行分析,得到考虑了接触比影响的裂纹平均闭合量为[10]:
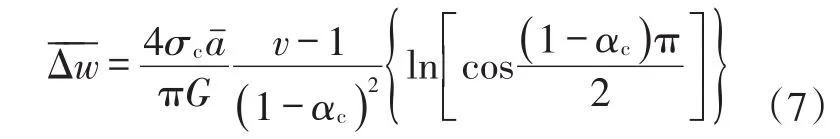
将裂缝的最小宽度与式(7)计算的裂纹平均闭合量进行比较。若裂纹平均闭合量大于最小缝宽,即(>wmin),就会有更多的粗糙颗粒相互接触。进一步计算各个裂缝宽度与最小缝宽间的差值(wi-wmin),为下一步的计算求得新的缝宽剖面。随着裂缝进一步闭合,用于表征未闭合裂纹的椭圆变得越来越小。若计算的裂纹变形量大于用于表征裂纹的椭圆的最大宽度,裂纹就会完全闭合。与此同时,随着两个粗糙壁面的接触比的增大,裂纹的变形量会急剧降低。重复上述过程直到裂缝不再闭合为止。图4给出了裂缝的闭合过程。
在闭合压力的作用下,一些宽度较大的裂纹不会完全闭合。此时,由式(7)求得的裂纹闭合量小于裂缝的最小宽度(<wmin)。那么,就可以求得最终的裂缝宽度剖面,即为(wi-)。在闭合压力为70MPa情况下模拟缝宽分布(图5)。
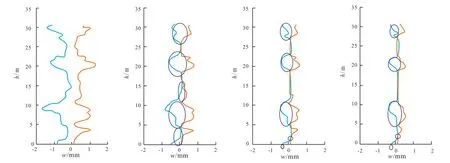
图4 裂缝的闭合过程Fig.4 Process of fracture closure
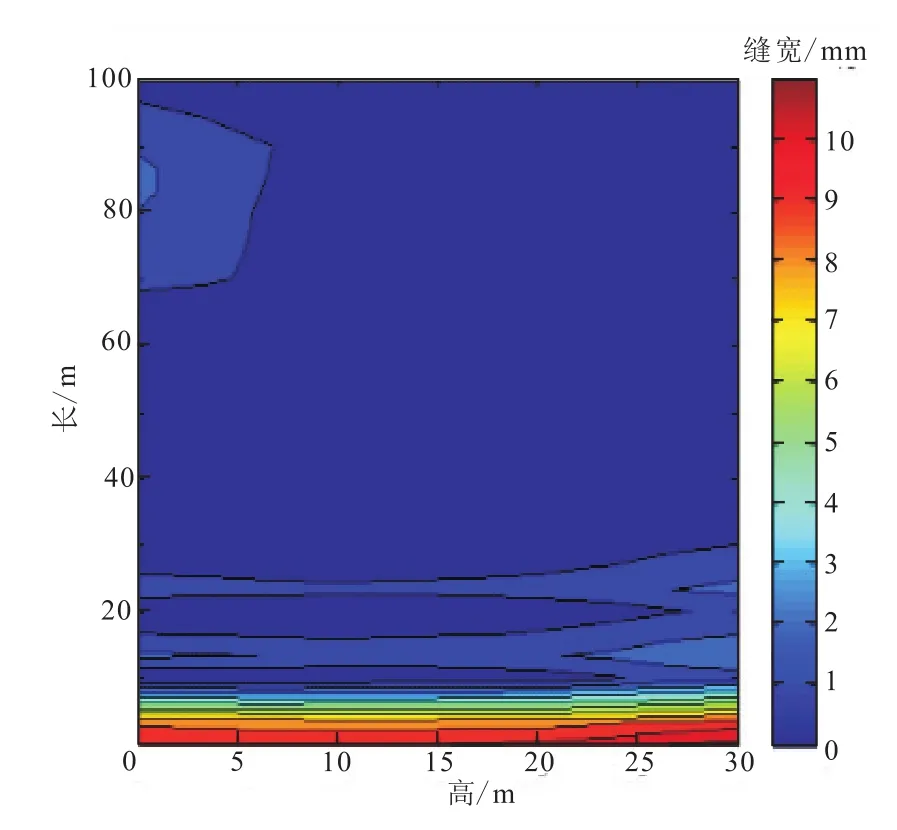
图5 闭合压力为70 MPa的条件下,闭合酸蚀裂缝的缝宽分布Fig.5 Distribution of width closed acid corrosion fractures with the closed pressure of 70 MPa
4 闭合酸蚀裂缝导流能力影响因素分析
4.1 导流能力计算
Zimmerman和Bodvarsson[1]对稳态Navier-Stokes方程进行了求解。假设裂缝是由两块平行板构成,裂缝导流能力为:

式中:w为裂缝宽度,m;Cf为裂缝导流能力,μm2·cm。
若将裂缝划分成若干个很小的网格单元,那么就可以将网格内的裂缝壁面近似为两块平行板,就可以利用立方规律对其导流能力进行计算,这就是局部立方规律(LCL)。Brush和Tomson[1]合成了一个粗糙裂缝,模拟流体在该裂缝中的流动情况。他们将Navier-Stokes方程、Stokes方程及LCL方程的计算结果进行对比后发现,LCL方程可以近似代替Navier-Stokes方程。所以,采用LCL方程计算闭合酸蚀裂缝导流能力。
由于裂缝宽度比裂缝长度和裂缝高度都要小得多,所以忽略流体在垂直于裂缝表面方向上的流动,将速度场式(9)、式(10)带入可以得到二维质量平衡方程得到式(11)。
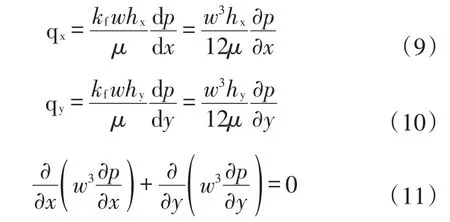
求得的闭合酸蚀裂缝宽度分布剖面的基础上,对式(11)进行离散并求出其数值解,求出裂缝中的压力分布。然后结合式(9)、式(10)中速度场分布可计算出闭合酸蚀裂缝导流能力:

式中:Cf为裂缝导流能力,μm2·cm;q为流速,m3/s;μ为流体黏度,mPa·s;xf为裂缝长度,m;hf为裂缝高度,m;Δp为裂缝两端的压差,MPa。
在求解闭合酸蚀裂缝导流能力的过程中,忽略裂缝剖面间的相互影响和裂缝中某些闭合区域的影响是不合理的。酸蚀裂缝壁面上的粗糙颗粒能让酸蚀裂缝在闭合压力的作用下不会完全闭合,刻蚀沟槽的形成有助于提高闭合酸蚀裂缝的导流能力[17,18]。
4.2 正交试验方案
影响闭合酸蚀裂缝导流能力的参数有很多,若要对所有参数的所有组合都进行分析是很困难的。因此,采用正交分析法选取影响闭合酸蚀裂缝导流能力的代表性参数组合进行分析。各影响因素的取值见表2。不考虑各个影响因素之间的相互作用,模拟次序及试验结果如表3所示。
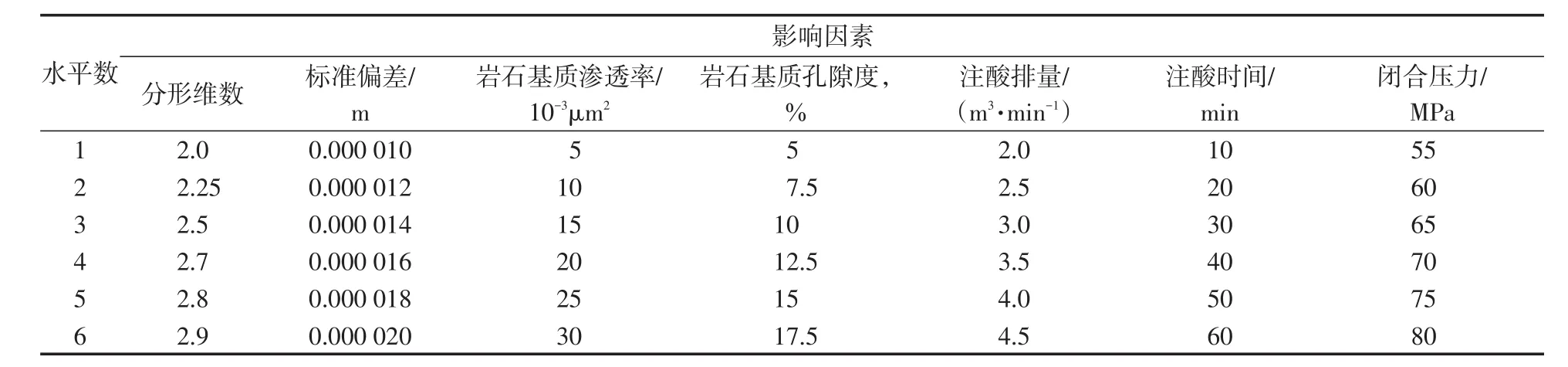
表2 闭合酸蚀裂缝导流能力模拟影响因素及因素水平Table2 Influence factors and factor levels of conductivity of closed acid fractures
4.3 试验结果分析
在正交实验设计理论中,各因素的极差大小反映该因素对闭合酸蚀裂缝导流能力的重要程度。从表4分析可知,分形维数、标准偏差、岩石基质渗透率、岩石基质孔隙度、注酸排量、注酸时间和闭合压力对闭合酸蚀裂缝导流能力的影响程度排序为:闭合压力>分形维数>注酸时间>地层基质渗透率>注酸排量>标准偏差>地层基质孔隙度。
通过以上分析可知,闭合压力是影响酸蚀裂缝导流能力最为重要的因素,前期对地质油藏的掌握,特别是裂缝闭合压力是准确预测导流能力指导施工的基础,分形维数也是制约导流能力的关键,在渗透率和孔隙度二者之间应该着重选择渗透率较高的层段作为施工层段。落实到工程上来看,注酸时间比注酸排量对导流能力的影响更大,在施工时严格把控时间,保持排量的稳定是获得高导流能力的必要条件与手段。
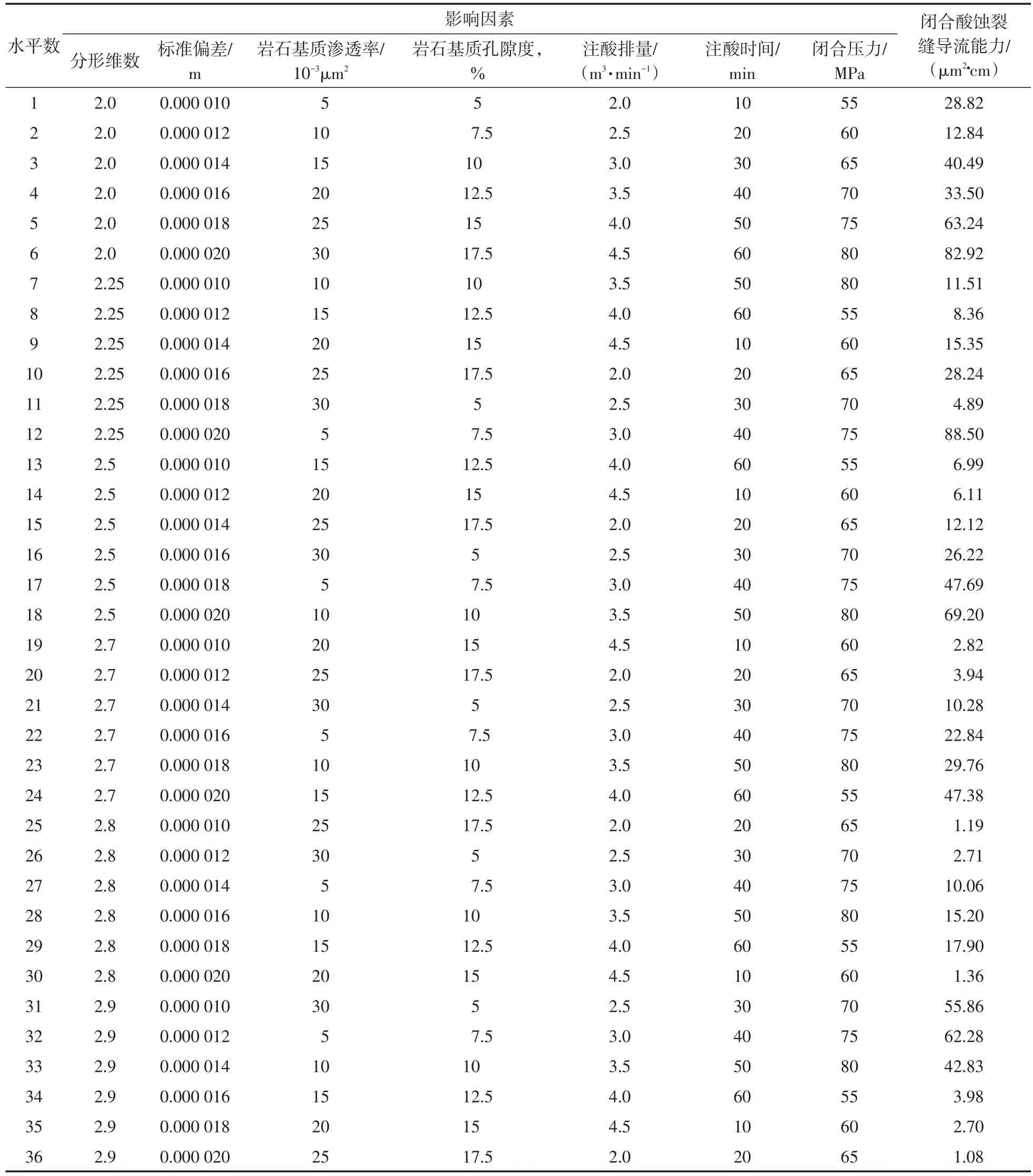
表3 正交试验次序及试验结果Table3 Orthogonal test order and results
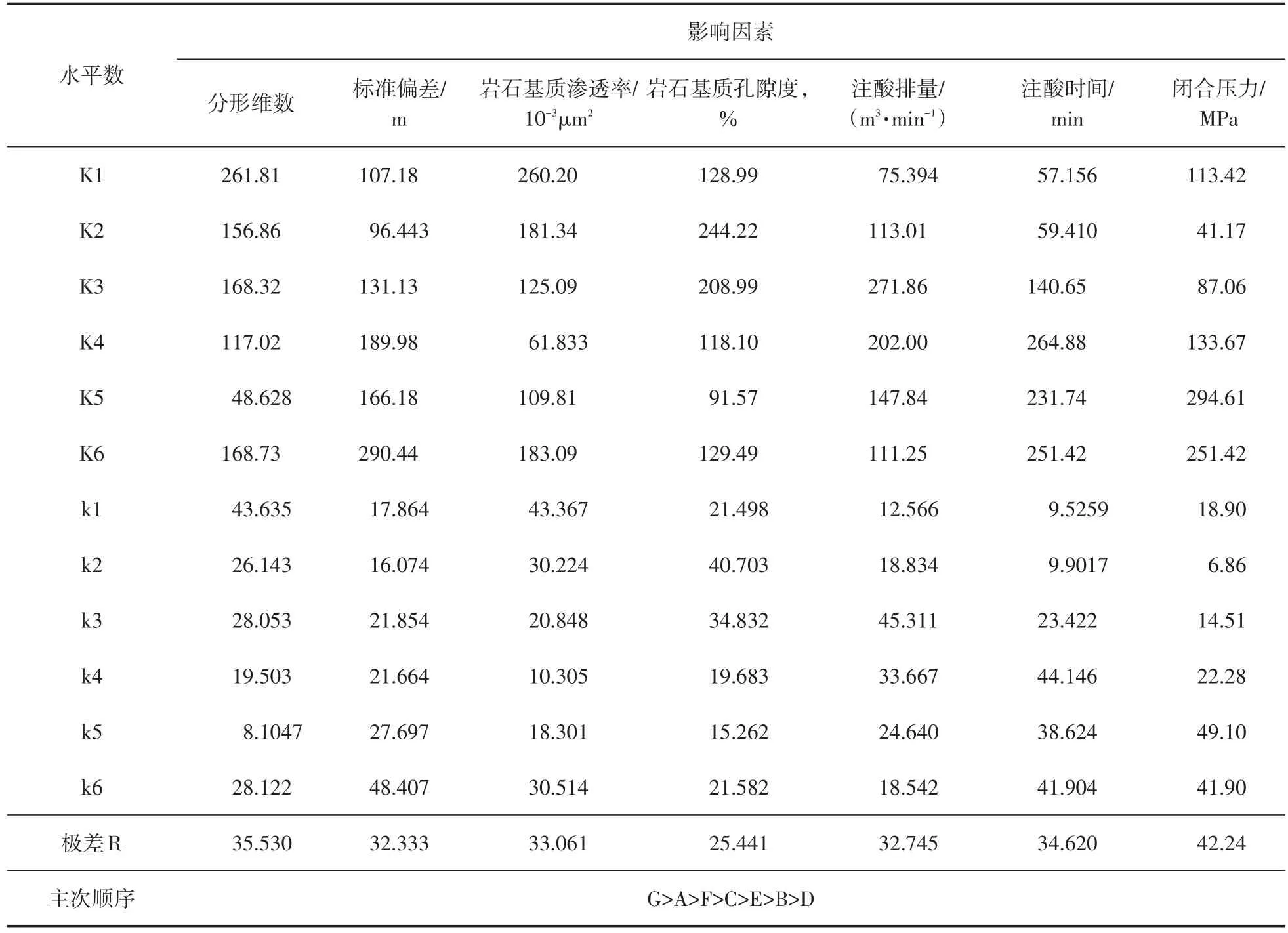
表4 试验结果分析Table4 Analysis of test results
5 结论
1)目前对于酸蚀裂缝几何形态和酸穿距离的计算模型较多,就酸蚀裂缝导流能力的计算模型研究较少。基于分形理论、流体力学方程和Myer闭合模型,模拟酸蚀裂缝闭合后的导流能力。
2)闭合酸蚀裂缝导流能力受闭合压力、基质渗透率、分形维数、注酸时间等多个参数的影响,利用正交分析法得到了影响闭合酸蚀裂缝导流能力主要因素的影响程度的排序:闭合压力>分形维数>注酸时间>地层基质渗透率>注酸排量>标准偏差>地层基质孔隙度。
3)通过前期地质认识,掌握闭合压力能很大程度上验证酸蚀裂缝导流能力预测的准确性,施工过程中注酸时间与注酸排量的保证是获得高导流能力的必要条件与手段。
