单坡光伏车棚风洞试验研究
2019-04-22李寿科刘智宇方湘璐高闻靖孙洪鑫
李寿科, 刘智宇, 张 雪, 方湘璐, 高闻靖, 孙洪鑫
(湖南科技大学 土木工程学院,湖南 湘潭 411201)
随着光伏发电技术的日益成熟,光伏发电系统组件被广泛安装于停车棚屋面。光伏发电系统组件替代了传统屋面,与停车棚支架形成一整体结构体系(后文中称为光伏车棚屋面)。风荷载为光伏车棚屋面结构设计的控制性荷载之一,是整个支撑系统主要受力构件和局部围护结构抗风设计所必须考虑的重要因素。国内外对于光伏组件的抗风研究主要集中在民居建筑屋面光伏系统和地面光伏系统[1-6],对于光伏车棚屋面的抗风研究却较少有涉及。光伏车棚屋面采用四面开敞式布置,以单坡屋面形式为主,风荷载特性较封闭屋面结构有较大的区别,与《建筑结构荷载规范》(GB50009—2012)中规定的四面开敞式单坡顶盖类似,规范指出这类结构为风敏感结构[7]。停车棚屋面的结构抗风设计可以通过类比一些四面开敞式单坡顶盖的风洞试验数据和国家规范进行。Gumley[8]对于一边开敞单坡屋面进行了1∶75缩尺比刚性模型测压风洞试验,采取准静态和联合极值分析方法,将试验结果与规范值进行对比,指出现行规范对于此类结构的设计取值不够合理。Uematsu等[9-10]对四面开敞单坡屋面进行了1∶100缩尺刚性模型测压风洞试验,研究了屋面风压随结构倾角变化的规律,与澳大利亚规范进行了对比,给出设计建议取值,其试验考虑的屋面倾角为0°~15°。《建筑结构荷载规范》(GB50009—2012)给出了屋面倾角范围为0°~30°的单坡顶盖垂直屋檐风向下的风荷载整体体型系数,但对于计算围护构件的局部体型系数未给出取值方法。光伏车棚屋面主体承重结构抗风设计需考虑整体体型系数取值,单块光伏组件抗风设计将由局部体型系数和极值风压系数决定。而光伏车棚屋面为适用于更大的发电量需要,较未安装光伏组件的车棚屋面具有更大的屋面倾角,在我国的强/台风区域倾角多采用20°~30°倾角[11],国内外文献对于此类大屋面倾角结构的整体和局部风荷载特性的研究较少,也没有给出用于围护结构设计的局部体型系数和极值风荷载取值方法。
本文制作了缩尺比为1∶50的四面开敞式单坡光伏车棚屋面,考虑3种屋面倾角(10°、20°、30°)和是否停车等工况,进行刚性模型测压风洞试验,研究屋面的整体体型系数,测点平均风压和极值风压、以及局部分块体型系数和极值风压的分布规律,与当今规范进行对比研究,给出光伏车棚屋面的整体体型系数和局部风荷载设计建议取值,为补充相关规范和标准提供参考。
1 刚性模型测压风洞试验概况
本次试验是在湖南科技大学的大气边界层风洞中进行。该风洞为开口直流吸入式矩形截面风洞,试验段的尺寸为4 m宽、3 m高、21 m长。试验模拟了《建筑结构荷载规范》GB50009—2012中的B类地貌,风场缩尺比为1∶50,平均风剖面指数为0.15,模型高度5 cm处对应湍流度为0.16,规范和试验平均风速以及湍流度剖面,如图1所示。

图1 平均风速及湍流度剖面Fig.1 Wind profile of tests
光伏车棚屋面足尺平面尺寸为12 m×6 m,下屋檐高2.5 m,试验考虑三种不同屋面倾角β(10°、20°和30°),模型缩尺比为1∶50,模型照片如图2所示。试验模型上下表面布置测点,测点布置如图3(b)所示,上下表面测点共计为32个,上下表面测点位置对应。试验风向角θ定义见图3,风向角间隔10°,每个工况共36个测试风向角。采样时长约30 s,采样频率330 Hz,采集10 000个数据样本。试验参考高度为屋面下屋檐高度。

图2 风洞试验模型Fig.2 Wind tunnel test model
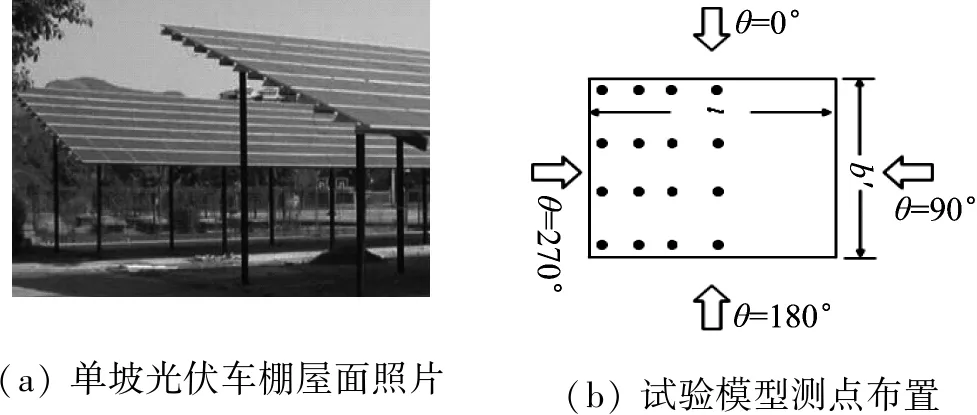
(a) 单坡光伏车棚屋面照片(b) 试验模型测点布置
图3 光伏车棚屋面照片和风向角定义及测点布置图
Fig.3 Photo of solar car parking mono-sloped roof and taps location of model
2 数据处理
风压系数是结构风压的无量纲表现形式,测点i的风压系数Cpi(t)定义如下:
(1)
式中:pi(t)为风洞试验中压力扫描阀测得的风压时程;p0为风洞试验段处的静压,采用皮托管测得;ρ为空气密度,取ρ=1.225 kg/m3;uh为参考高度屋面平均高度处的平均风速。对Cpi(t)做数据统计可得测点平均风压系数Cpi,mean以及脉动风压系数Cpi,rms。
测点的极大值风压系数Cpi,max和极小值风压系数Cpi,min定义如下:
Cpi,maxmin=Cpi,mean±g×Cpi,rms
(2)
式(2)中g为峰值因子,按照规范取为3.5,未考虑风压系数的非高斯特征,暂时按照规范方法简化处理。
定义Cpu,i(t)和Cpd,i(t)分别为上下表面测点风压系数时程,其净压测点的风压系数时程为:
Cpn,i(t)=Cpu,i(t)-Cpd,i(t)
(3)
依据统计方法可得净平均风压系数、净脉动风压系数、净压测点的极大值风压系数和极小值风压系数。净压测点平均风压系数的参考高度取为测点高度可得测点体型系数μsi。通过对单坡屋面进行分区处理,各分区风荷载体型系数定义如下:
(4)
式中:Ai为测点的从属面积;n为分区测点总数。下文中如无特殊说明,分析结果均为净压测点风压系数或体型系数。
3 数据分析和结果
3.1 整体体型系数
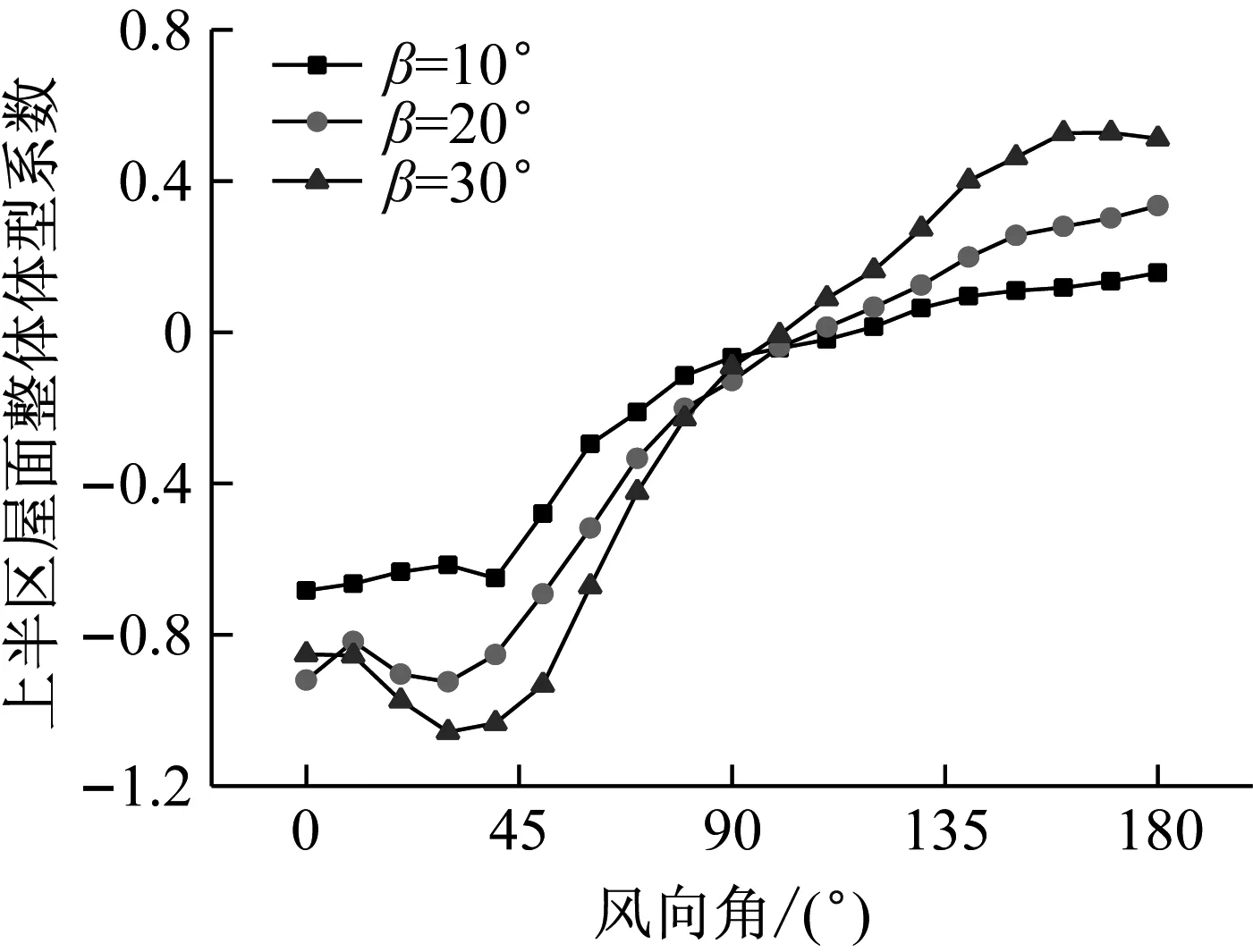
图4给出了单坡光伏车棚屋面(β=10°、20°、30°)的整体体型系数随风向角的变化规律。由图4可以看出,对于位置较高的上半区单坡屋面,倾角为10°时,体型系数在-0.68~0.15范围内变化,倾角为20°时,体型系数在-0.92~0.33范围内变化,倾角为30°时,体型系数在-1.06~0.51范围内变化,上半区屋面整体平均风荷载随屋面倾角的增大而增加。整体风吸力大于整体风压作用,最不利风向发生在斜风向。
(a) 位置较高的上半区单坡屋面
(b) 位置较低的下半区单坡屋面
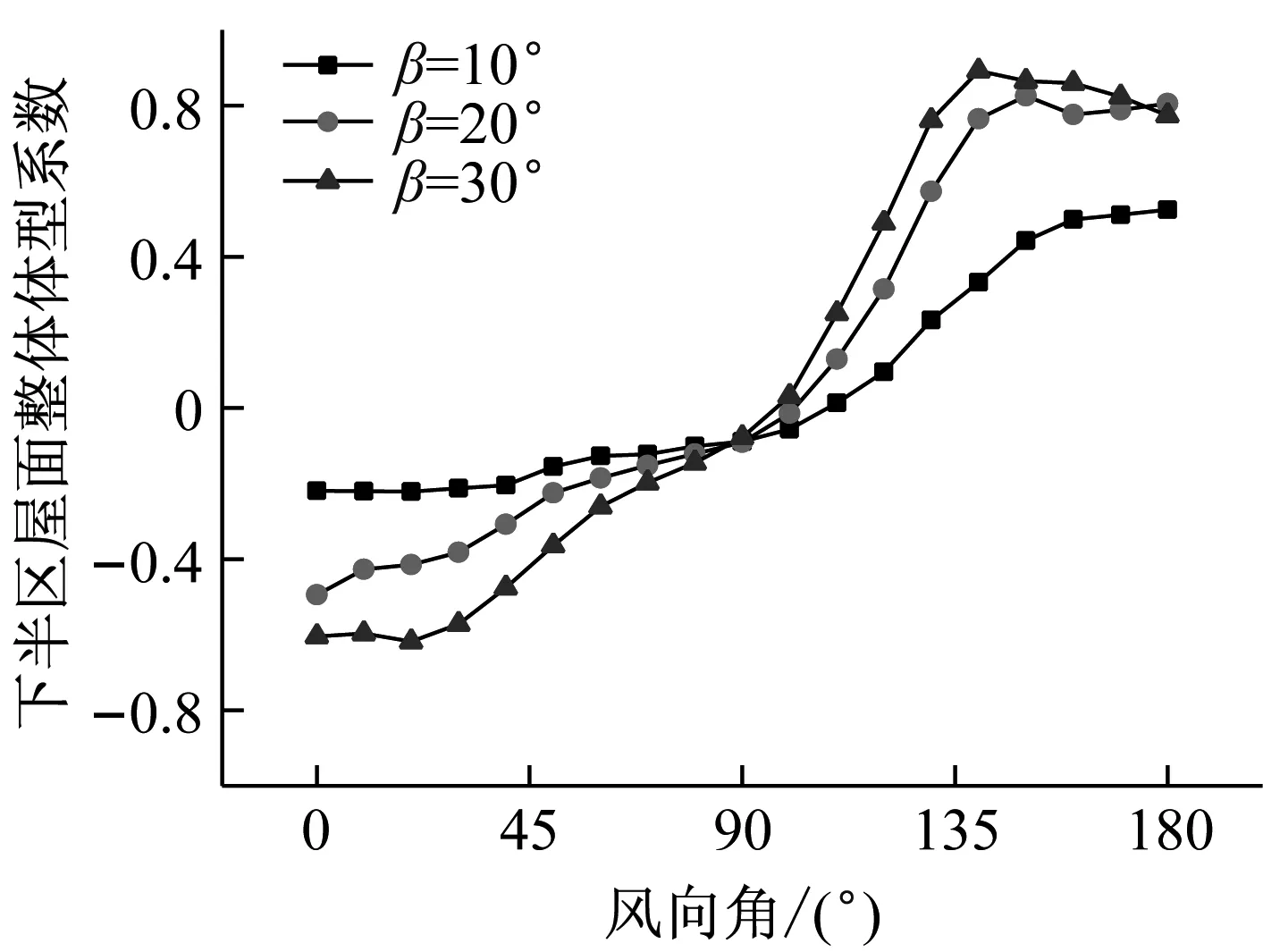
图4 单坡车棚屋面(β=10°、20°、30°)整体体型系数随风向角的变化(0°~180°风向)
Fig.4 Overall shape coefficients between 0° and 180°wind angle for roof pitches 10°、20° and 30°
对于位置较低的下半区单坡屋面(μs1),倾角为10°时,体型系数在-0.22~0.52范围内变化,倾角为20°时,体型系数在-0.49~0.83范围内变化,倾角为30°时,体型系数在-0.62~0.89范围内变化,下半区屋面整体平均风荷载随屋面倾角的增大而增加。整体风压力大于整体风吸作用,最不利风向发生在斜风向。
通过对比可以看出,上半区屋面主要承受风吸作用,下半区屋面主要承受风压作用,屋面整体平均风荷载随屋面倾角的增大而增加。
表1给出了单坡车棚屋面(β=10°、20°、30°)的整体体型系数与《建筑结构荷载规范》GB50009—2012的单坡顶盖体型系数比较。如表2所示,与规范值对比可知,垂直风向单坡车棚屋面试验值比规范取值小约30%,最不利斜风向单坡车棚屋面试验值比规范取值小约20%。试验值与美国规范取值相差较大,垂直风向单坡车棚屋面试验值比澳洲规范取值小约23%。
表1单坡屋面整体体型系数最大试验值与规范值对比
Tab.1ComparisonfortheoverallshapecoefficientsbetweentestsandChinesestandard

内容Β0°风向角180°风向角μs1μs2μs1μs2中国规范值10°-0.50-1.301.300.50试验值10°-0.22-0.680.52 0.16中国规范值20°-0.55-1.351.350.55ASCE7-1020°-0.30-2.402.200.70AS/NZS117020°-0.75-1.201.050.53试验值20°-0.49-0.920.810.33中国规范值30°-0.60-1.401.400.60试验值30°-0.60-0.850.770.51
3.2 测点平均风压系数
图5和图6分别给出了单坡倾角20°光伏车棚屋面风向角为0°、40°时平均风压系数等值线图。当风向角为0°时,屋面上表面迎风,净平均风压系数在-0.25~-0.67范围内变化,最不利值出现在上屋檐两侧的角部;风向角为40°时,屋面上表面迎风,上表面风压系数在风向的左右两侧表现出强烈的锥形涡,而下表面风压系数分布平行于迎风长边数值大小依次递减,净平均风压系数在-0.03~-1.62范围内变化,最不利值出现在上屋檐右侧的角部。
3.3 测点极值风压系数
图7、8分别给出了0°~180°风向下单坡10°、20°、30°最不利极大值和极小值风压系数等高线图。从图7中可以看出,对于最不利极大值风压系数,下屋檐极值风压力大于上屋檐极值风压力,随着屋面坡角增大,最不利极大值风压系数增加,最大极值风压力出现在下屋檐角部区域。从图8中可以看出,对于最不利极小值风压系数的绝对值,上屋檐极值风吸力大于下屋檐极值风吸力,随着屋面坡角增大,最不利极值风吸力增加,全风向最大极值风吸力出现在角部区域。
3.4 局部分块风荷载设计建议取值
参照《建筑结构荷载规范》GB50009—2012中屋面分区方式,图9给出了对单坡屋面分区方式。基于风洞试验的结果,给出各个分区在所有风向角范围内的最不利正体型系数、最不利负体型系数、最不利极大值风压系数和最不利极小值风压系数,便于光伏系统组件抗风设计。

(a) 上表面

(b) 下表面
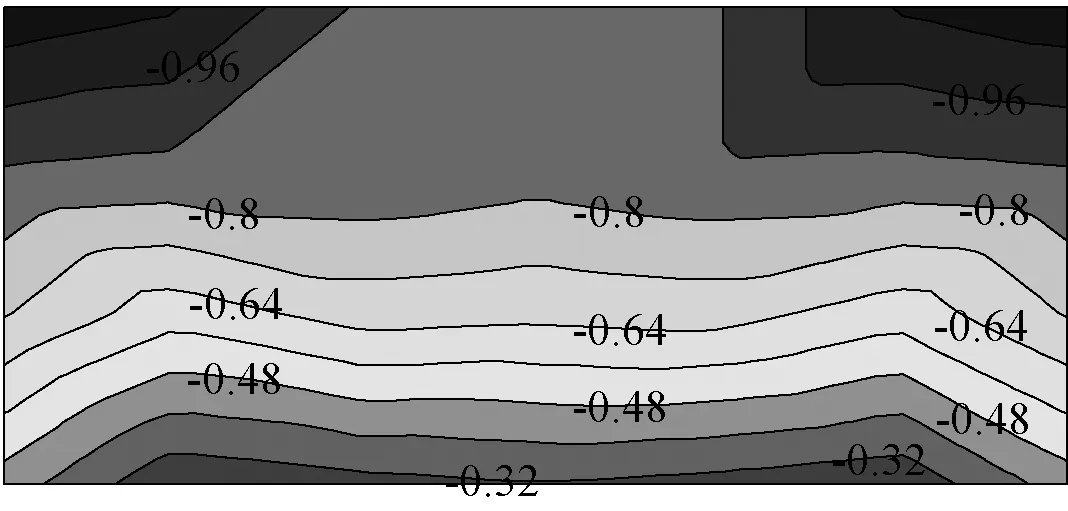
(c) 净压图5 单坡20°屋面在0°风向角下平均风压系数等值线图Fig.5 Mean wind pressure coefficients of roof with pitch 20°(Wind angle of 0°)
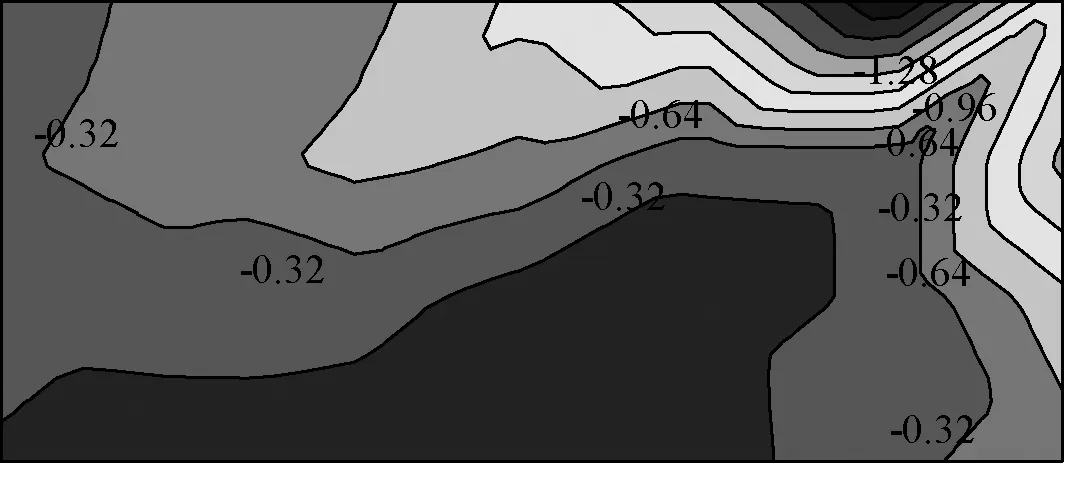
(a) 上表面
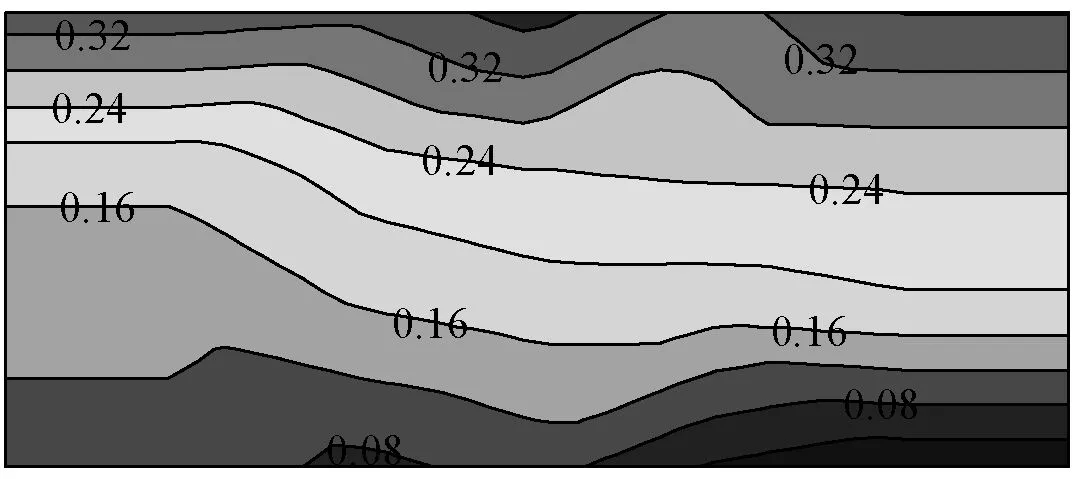
(b) 下表面

(c) 净压图6 单坡20°屋面在40°风向角下平均风压系数等值线图Fig.6 Mean wind pressure coefficients of roof with pitch 20°(Wind angle of 40°)

(a) 单坡10°

(b) 单坡20°
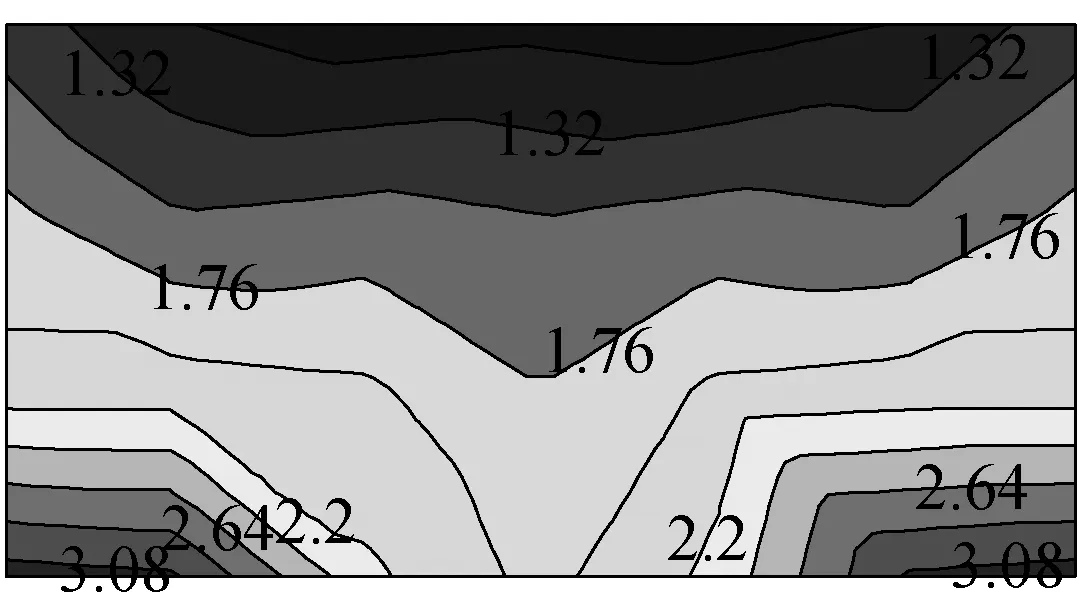
(c) 单坡30°图7 单坡10°、20°、30°屋面最不利极大值风压系数Fig.7 The most critical maximum wind pressure coefficients of roof with pitches 10°、20°、30°

(a) 单坡10°
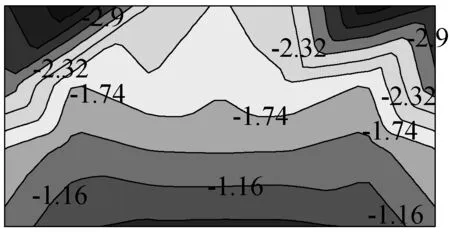
(b) 单坡20°

(c) 单坡30°图8 单坡10°、20°、30°屋面最不利极小值风压系数Fig.8 The most critical minimum wind pressure coefficients of roof with pitches 10°、20°、30°
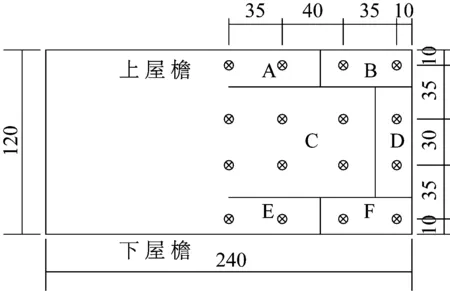
图9 单坡车棚屋面体型系数分区Fig.9 The block of mono-sloped roof
表2给出了倾角为10°时单坡停车棚屋面全风向下最不利正、负体型系数、以及最不利极大和极小值风压系数结果。由表2可以看出,最大正体型系数(0.98)出现在屋面的下屋檐角部F区域,最小负体型系数(-0.99)出现在屋面的上屋檐角部B区域,其对应的位置会产生最不利的极大值风压和极小值风压。
表3给出了倾角为20°时单坡停车棚屋面全风向下最不利正、负体型系数、以及最不利极大和极小值风压系数结果。由表3可以看出,最大正体型系数(1.79)出现在屋面的下屋檐角部F区域,最小负体型系数(-1.49)出现在屋面的上屋檐角部B区域,其对应的位置会产生最不利的极大值风压和极小值风压。
表4给出了倾角为30°时单坡停车棚屋面全风向下最不利正、负体型系数、以及最不利极大和极小值风压系数结果。由表4可以看出,最大正体型系数(1.59)出现在屋面的下屋檐角部F区域,最小负体型系数(-1.88)出现在屋面的上屋檐角部B区域,其对应的位置会产生最不利的极大值风压和极小值风压。
对比表2、表3和表4可以看出,坡角增加,屋面承受的风荷载会增大(风压和风吸作用均增加)。
表2分区体型系数/极值风压系数取值(单坡屋面倾角10°)
Tab.2Theproposedvaluesofblockshapecoefficientsandminimumwindpressurecoefficients(β=20°)
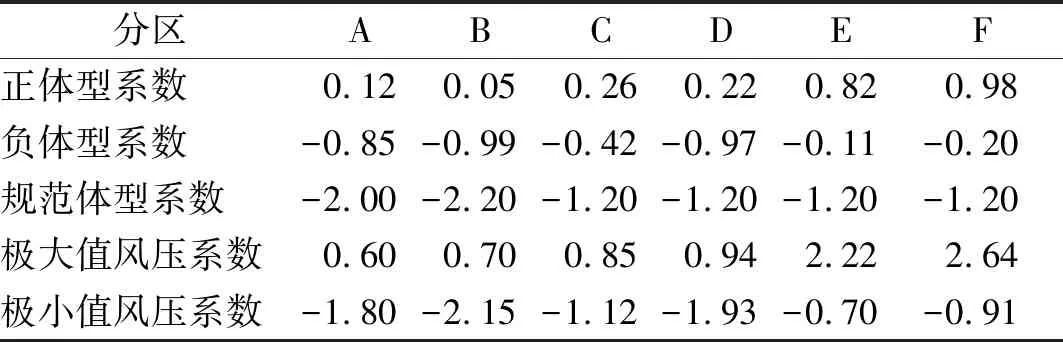
分区ABCDEF正体型系数0.120.050.260.220.820.98负体型系数-0.85-0.99-0.42-0.97-0.11-0.20规范体型系数-2.00-2.20-1.20-1.20-1.20-1.20极大值风压系数0.600.700.850.942.222.64极小值风压系数-1.80-2.15-1.12-1.93-0.70-0.91
将20°倾角单坡光伏车棚屋面试验值(表3)与《建筑结构荷载规范》GB50009—2012中的封闭式房屋局部体型系数对比研究可以发现;①规范值仅对针对吸力,没有考虑不利风向角的风压作用,对于四面敞开式的车棚结构,风荷载正体型系数在屋面边缘和下屋檐位置亦较大,可达1.59;②对于敞开式的单坡屋面,按照封闭式房屋进行设计不准确,车棚上屋檐屋面的边缘区域试验值低于封闭式房屋规范值,在屋面的中部区域试验值高于封闭式房屋规范值,在下屋檐屋面的边缘区域试验值低于封闭式房屋规范取值。
表3分区体型系数/极值风压系数取值(单坡屋面倾角20°)
Tab.3Theproposedvaluesofblockshapecoefficientsandminimumwindpressurecoefficients(β=20°)
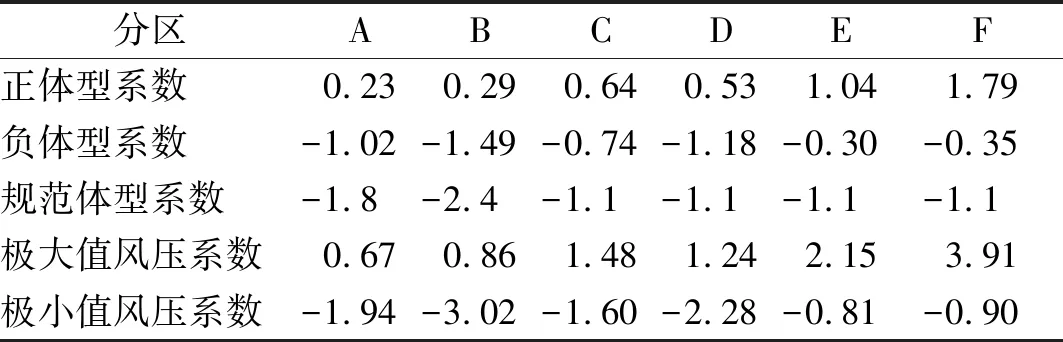
分区ABCDEF正体型系数0.230.290.640.531.041.79负体型系数-1.02-1.49-0.74-1.18-0.30-0.35规范体型系数-1.8-2.4-1.1-1.1-1.1-1.1极大值风压系数0.670.861.481.242.153.91极小值风压系数-1.94-3.02-1.60-2.28-0.81-0.90
表4分区体型系数/极值风压系数取值(单坡屋面倾角30°)
Tab.4Theproposedvaluesofblockshapecoefficientsandminimumwindpressurecoefficients(β=30°)
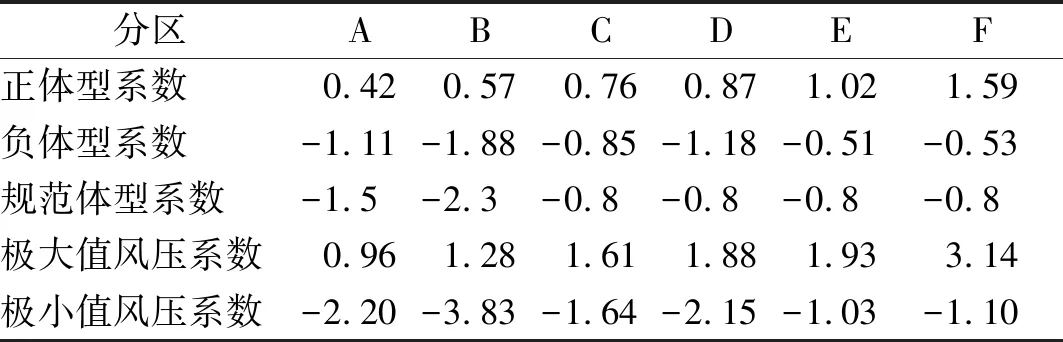
分区ABCDEF正体型系数0.420.570.760.871.021.59负体型系数-1.11-1.88-0.85-1.18-0.51-0.53规范体型系数-1.5-2.3-0.8-0.8-0.8-0.8极大值风压系数0.961.281.611.881.933.14极小值风压系数-2.20-3.83-1.64-2.15-1.03-1.10
3.5 停车对光伏车棚屋面风荷载的影响
图10和图11分别给出了单坡车棚屋面在20°倾角、停车工况下风向角为0°和180°的平均风压系数等值线图。当风向角为0°时,屋面下表面迎风承受风压作用,平均风压系数在-0.60~-0.40范围内变化,上表面背风,平均风压系数在-0.35~-0.65范围内变化,净风压系数在-0.30~-0.96范围内变化,最不利值出现在上屋檐两侧的角部和迎风边缘。

(a) 上表面

(b) 下表面
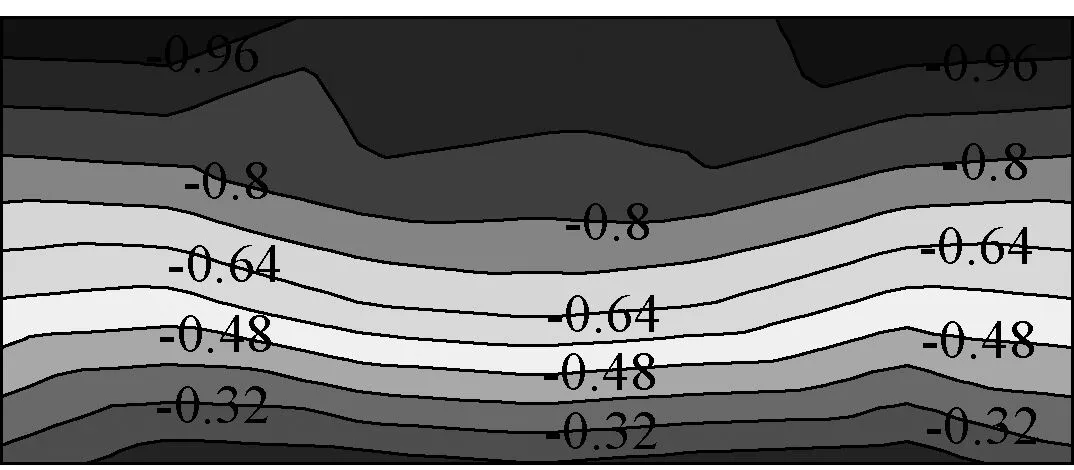
(c) 净压图10 停车工况下屋面平均风压系数等值线图(20度倾角,0°风向)Fig.10 Mean wind pressure coefficients of roof with car parking (β=20°,θ=0°)
当风向角为180°时,屋面上表面迎风,上表面下屋檐承受风压作用,上表面上屋檐处于气流分离区,上表面平均风压系数在-0.08~0.20范围内变化,下表面背风,平均风压系数在-0.52~-0.24范围内变化,由于停车干扰的影响,其等值线不平行于屋檐,且风吸力要小于无车工况,净风压系数在0.14~0.70范围内变化,最不利值出现在下屋檐迎风边缘。
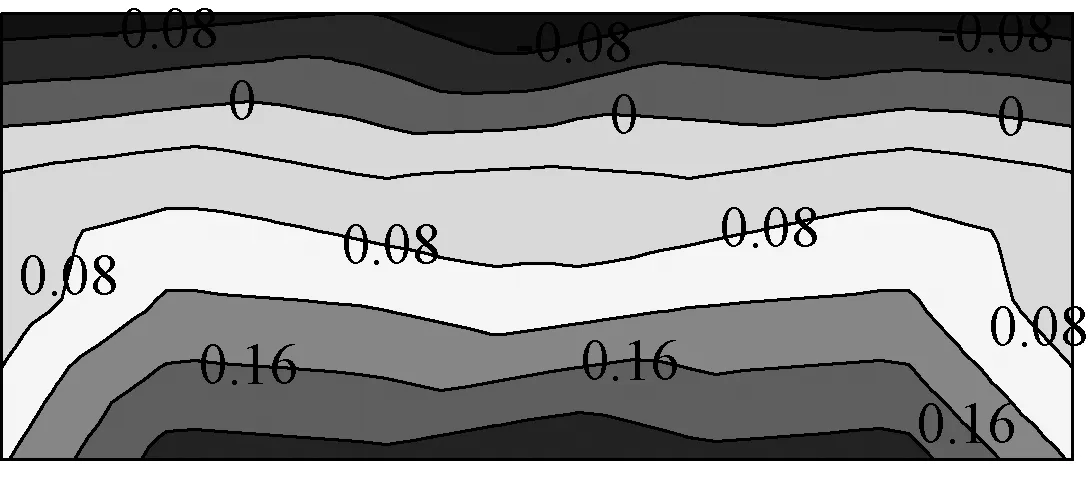
(a) 上表面
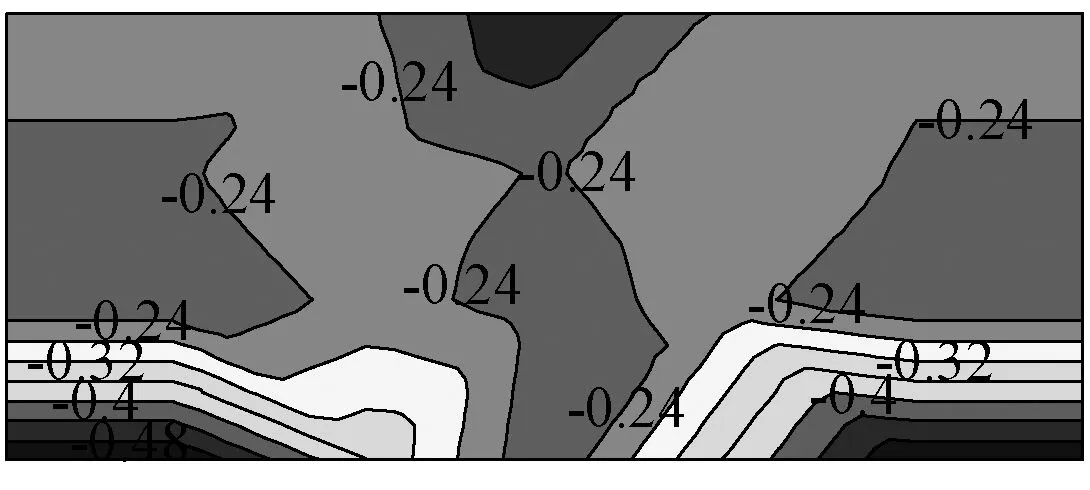
(b) 下表面

(c) 净压图11 停车工况下屋面平均风压系数等值线图(20度倾角,180°风向)Fig.11 Mean wind pressure coefficients of roof with car parking (β=20°,θ=180°)
图12给出了车棚阻塞(无车、停车)对单坡车棚屋面(β=20°)体型系数随风向角的变化规律。对于位置较高的上半区屋面(μs2),停车会增加车棚的上半区屋面风吸力约10%,其承受的风压变化不明显;对于位置较低的下半区屋面(μs1),停车对其整体平均风吸力影响较小,而对于90°~180°风向范围的风压作用影响较为明显,减小幅值大约为70%,其原因为停车遮挡效应会使位置较低的下半区单坡屋面的下表面平均风荷载减小。

(a) 位置较高的上半区单坡屋面
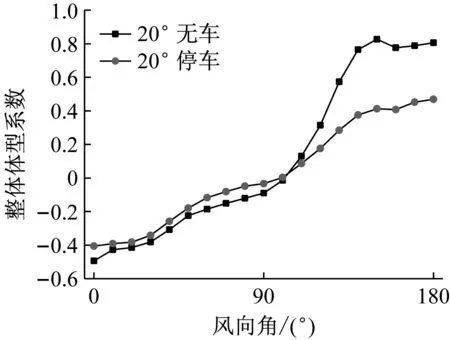
(b) 位置较低的下半区单坡屋面图12 无车和停车工况单坡车棚屋面(β=20°)体型系数随风向角的变化Fig.12 Overall shape coefficients for with car parking and without car parking case(β=20°)
表5给出了屋面倾角为20°时,单坡光伏车棚屋面各分块在停车和无车工况下全风向范围内的最不利正、负体型系数以及最不利极大、极小值风压系数结果对比。停车会减小屋面所有分区的最不利正体型系数,屋面各分块所受的最不利平均正风压和最不利极值正风压均减小。停车会增大上屋檐最不利平均风吸力和最不利极值风吸力,减小下屋檐的最不利风吸作用。
表5无车和停车工况下屋面分区体型系数/极值风压系数取值比较(单坡屋面倾角20°)
Tab.5Blockshapecoefficientsandminimumwindpressurecoefficientsforwithandwithoutcarparkingcases(β=20°)

分区ABCDEF正体型系数(无车)0.230.290.640.531.041.79负体型系数(无车)-1.02-1.49-0.74-1.18-0.30-0.35正体型系数(停车)0.140.160.320.390.520.70负体型系数(停车)-1.13-1.76-0.72-1.32-0.22-0.32极大值风压系数(无车)0.670.861.481.242.153.91极小值风压系数(无车)-1.94 -3.02 -1.60 -2.28 -0.81 -0.90 极大值风压系数(停车)0.530.700.841.091.991.81极小值风压系数(停车)-2.20-3.29-1.54-2.47-1.02-0.89
4 结 论
(1)单坡光伏车棚上半区屋面主要承受风吸作用,下半区屋面主要承受风压作用,屋面整体平均风荷载随屋面倾角的增大而增加,最不利整体风荷载试验值比规范取值小20%左右。
(2)下屋檐极值风压力大于上屋檐极值风压力,上屋檐极值风吸力大于下屋檐极值风吸力,随着屋面坡角增大,屋面最不利极值风荷载增加,全风向最大极值风吸力和风压力均可能出现在角部区域。
(3)随着坡角增加,屋面各分块承受的风荷载增大,对于敞开式的单坡光伏车棚屋面,按照封闭式房屋进行设计不准确,上屋檐角部分块为最不利风吸发生位置,下屋檐角部分块为最不利风压发生位置。
(4)停车会增大上半区屋面最不利平均风吸力和最不利极值风吸力,减小下半区屋面的最不利风压作用约为70%。
