基于Stewart平台的隔振与抑振协同控制研究

王嘉铭， 孔永芳， 黄 海

(北京航空航天大学 宇航学院，北京 100191)

随着高精度卫星遥感、空间光通信等应用的发展，星载有效载荷的精度指标不断提高，其对于工作环境平稳性的要求也更为严格。而在轨过程中，卫星本体与有效载荷自身均存在产生微振动的干扰源，如卫星本体上的动量轮[1]与太阳能电池阵驱动机构[2]、有效载荷携带的制冷机[3]与扫摆机构[4]，其中，前者称为间接干扰，后者称为直接干扰。这些干扰会降低载荷的工作精度，因此，对其进行振动控制是必要的。

间接干扰常通过振动隔离来减缓，即阻止振动向载荷传递，直接干扰常通过振动抑制来消除，即抑制载荷自身的振动。鉴于直接与间接干扰常同时存在，且频率成份复杂，故同时进行宽频带振动隔离与抑制(即宽带隔振与抑振协同控制)更有利于保证精密载荷的工作质量。针对星上微振动多自由度的特点，引入经典的六自由度并联机构Stewart平台作为精密载荷和卫星本体之间的连接装置，可同时实现多自由度振动的隔离与抑制[5]。

柔性Stewart平台常采用音圈电机并联弹簧的设计，具备高频被动隔振的能力，在此基础上，谢溪凌等[6-7]采用积分力反馈方法有效地压制了平台在共振峰处的振动，Chi等[8]采用鲁棒控制对低频振动进行了隔离。Lin等[9]采用了正向力反馈方法进行抑振，能够对3～15 Hz的直接干扰实现至多10 dB的抑制，抑振带宽并不理想。上述文献均是对宽带隔振或抑振的单独研究，并未考虑隔振与抑振的协同控制。

李伟鹏等[10]利用Skyhook和正向力反馈方法开展了单杆隔振与抑振协同控制实验，但并未进行整台实验。Cobb 等[11]分别基于线性时不变滤波算法和自适应陷波滤波器设计了隔振和抑振控制方法，将5 Hz以上的间接干扰隔离了20 dB、56 Hz的直接干扰引起的振动抑制了37 dB，但由于自适应陷波滤波器只能抑制已知频率的窄带干扰，故其无法用于宽带抑振。综上所述，当前未有宽带隔振与抑振协同控制的研究成果，仍需进一步研究。

针对上述问题，本文以音圈电机驱动的柔性Stewart平台为研究对象，以宽带隔振与抑振协同控制为研究重点，基于自适应滤波控制方法设计了隔振与抑振一体化控制器，并引入了Skyhook控制回路以提高控制系统的稳定性，通过仿真和实验验证了控制器在多自由度方向上均具有宽频带的隔振、抑振能力。

1 Stewart平台动力学特性分析

Stewart平台由上、下平板和六根伸缩杆组成，如图1所示，其中，上平板视为有效载荷，下平板与卫星本体固联，两者均视为刚体。{P}、{B}分别为固连在上、下平板质心处的本体坐标系，{U}为惯性坐标系，其与{B}系的初始位置重合，初始时刻，三个坐标系的坐标轴方位相互平行；Pi、Bi(i=1,2,…,6)分别为六根作动杆与上、下平板相连的铰接点。

图1 Stewart平台示意图Fig.1 The sketch of the Stewart platform

因作动杆中运动部分的质量相对于上平板的质量来说是非常小的，故建模时忽略该部分质量。将作动杆模型简化为弹簧阻尼+电机力模型，根据文献[12]，平台在关节空间中的动力学模型为

(1)

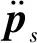
(2)

结合上述参数解算出Hij(s)，从解算出的Hij(s)具体表达式可知，Hij(s)的阶数均为十二阶，为高阶系统。

以Hi1(s)(i=1,2,…,6)为例，画出其幅频特性曲线，如图2所示。

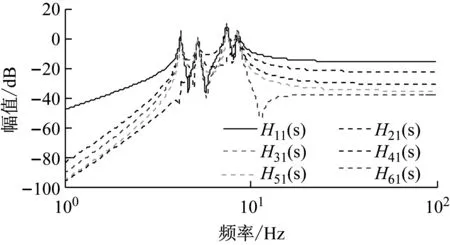
图2 H11(s)～H61(s)的幅频特性曲线Fig.2 Magnitude-frequency characteristic curves from H11(s) to H61(s)

由图2可以看出，在共振频率处，各杆的加速度响应大，阻尼比小；在远离共振频率的频域，H21的幅值相比于H11低了6 dB，其它四个传函的幅值更是低了15 dB以上，可见，杆1上控制力引起的其它杆加速度响应明显小于杆1自身的加速度响应，表明杆1与其它杆之间耦合较小。

分别查看当j=2,3,…，6时H1j(s)至H6j(s)的幅频特性曲线，均得出了杆j(j=2,…,6)与其它杆之间在非共振频域耦合较小的结论。综上可知，在远离共振频率的区域，各杆之间耦合较小。

2 控制器设计

本文的控制目标是当Stewart平台的上、下平板受到扰动时，通过控制器调整音圈电机控制力使上平板的加速度为零。

考虑到本文平台各杆间耦合较小的特点，为简化设计，采用了分散控制策略。在微振动环境下，六根杆上端沿杆向的加速度与上平板的加速度之间近似呈线性关系，那么当六根杆上端沿杆向加速度均趋近于零时，上平板的加速度也会趋近于零，故控制目标可以转化为当作动杆i的上端和下端受到扰动时，通过该杆控制器调整其音圈电机控制力的大小，使得该杆上端的杆向加速度响应趋近于零。

2.1 基于自适应滤波的控制器设计

通常星载精密载荷内部无法随意安装测量干扰源信号的传感器，而自适应滤波反馈控制[13-14]无需通过额外的传感器获取干扰信息，便可估计出干扰并将其消除，因此，本文以自适应滤波反馈控制为Stewart平台的振动控制方法。因该方法能估计并消除上平板所受的所有扰动，故其可以同时实现隔振与抑振。

对第i根作动杆实施单输入单输出的基于Filter-X Least Mean Square(FXLMS)算法的自适应滤波控制，系统的控制框图，如图3所示。

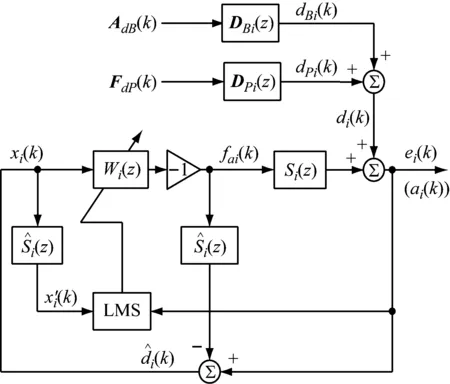
图3 作动杆i的控制框图Fig.3 Control loop ofithstrut

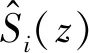
(3)

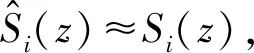
滤波器权系数向量的自适应律为

(4)

式中：Wi(k+1)=[wi,0(k+1),wi,1(k+1),…,wi,L-1(k+1)]T、Wi(k)=[wi,0(k),wi,1(k),…,wi,L-1(k)]T分别为k+1、k时刻的权系数向量，Xi(k)=[xi(k),xi(k-1),…,xi(k-L+1)]T为k时刻的参考信号向量，L-1为滤波器的阶数，μi为收敛因子。

对自适应控制而言，传感器的测量噪声可能会使权系数产生漂移，最终导致系统的突然发散。为了解决该问题，本文利用死区技术对自适应律进行修正[15]，即给误差信号一个阈值e0，当误差绝对值小于e0时权系数不更新，当绝对值大于e0时自适应机制开启。修正后的自适应律，如式(5)所示。

(5)

2.2 Skyhook控制回路的引入

由第1节可知控制通道的阻尼比小，这对FXLMS算法稳定性有着不利影响[16]，因此本文在各杆自适应滤波反馈控制回路的基础上引入了简单常用的增加主动阻尼的控制回路，即Skyhook[17]控制回路。

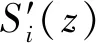
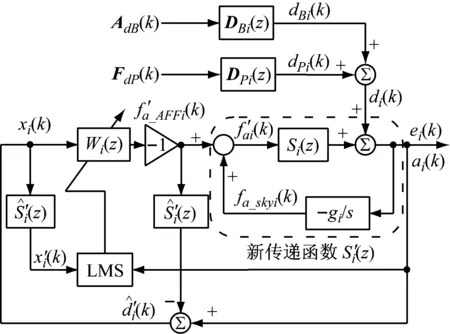
图4 作动杆i的带有Skyhook回路的控制框图Fig.4 Control loop with Skyhook ofithstrut

Skyhook方法的基本思想是产生与作动杆上端的绝对速度成正比的控制力进行负反馈，从而调节作动杆的阻尼特性，改变结构的振动响应特性。当对六根作动杆施加了Skyhook控制后，Stewart平台可以被看作一个新系统，自适应滤波控制则是对新系统做控制。

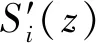
由图4可知，六个音圈电机总控制力组成的向量的拉氏变换可表示为

(6)

式中：

Fa_sky(s)可以写为

Fa_sky(s)=-G·A(s)·s-1

(7)

式中：G=diag(g1,…,g6)，gi为作动杆i的增益系数。

将式(6)和式(7)代入式(2)，整理得Fa_AFF(s)到A(s)的传递关系为

(G+B)s+K)-1Fa_AFF(s)=

H′(s)Fa_AFF(s)

(8)

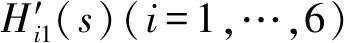
(a) 幅频特性

(b) 相频特性图至的频率特性曲线Fig.5 Magnitude-phase frequency characteristic curve

(9)

2.3 控制器稳定性

自适应滤波控制的稳定性由控制通道的估计误差和收敛因子的大小决定[18]。

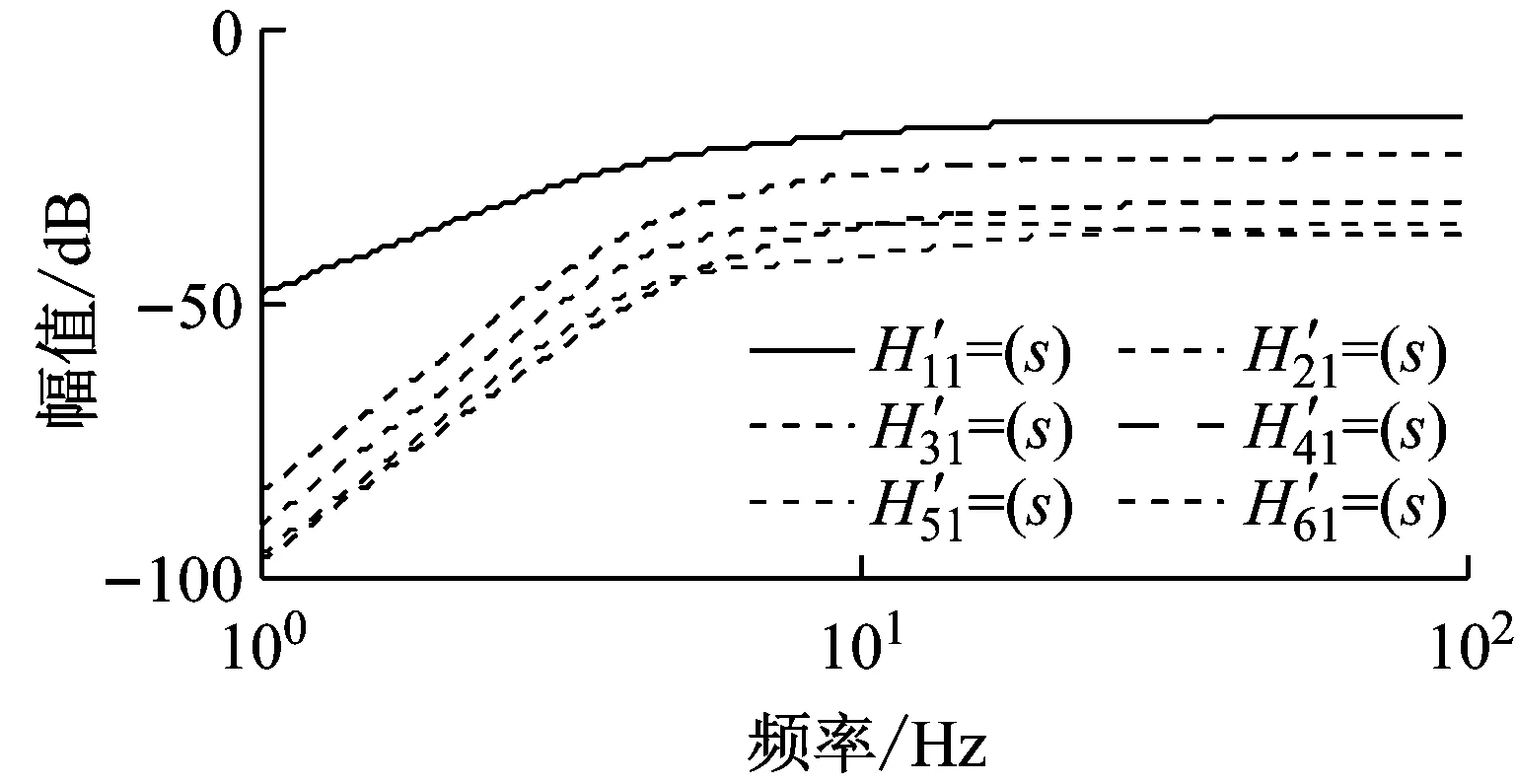
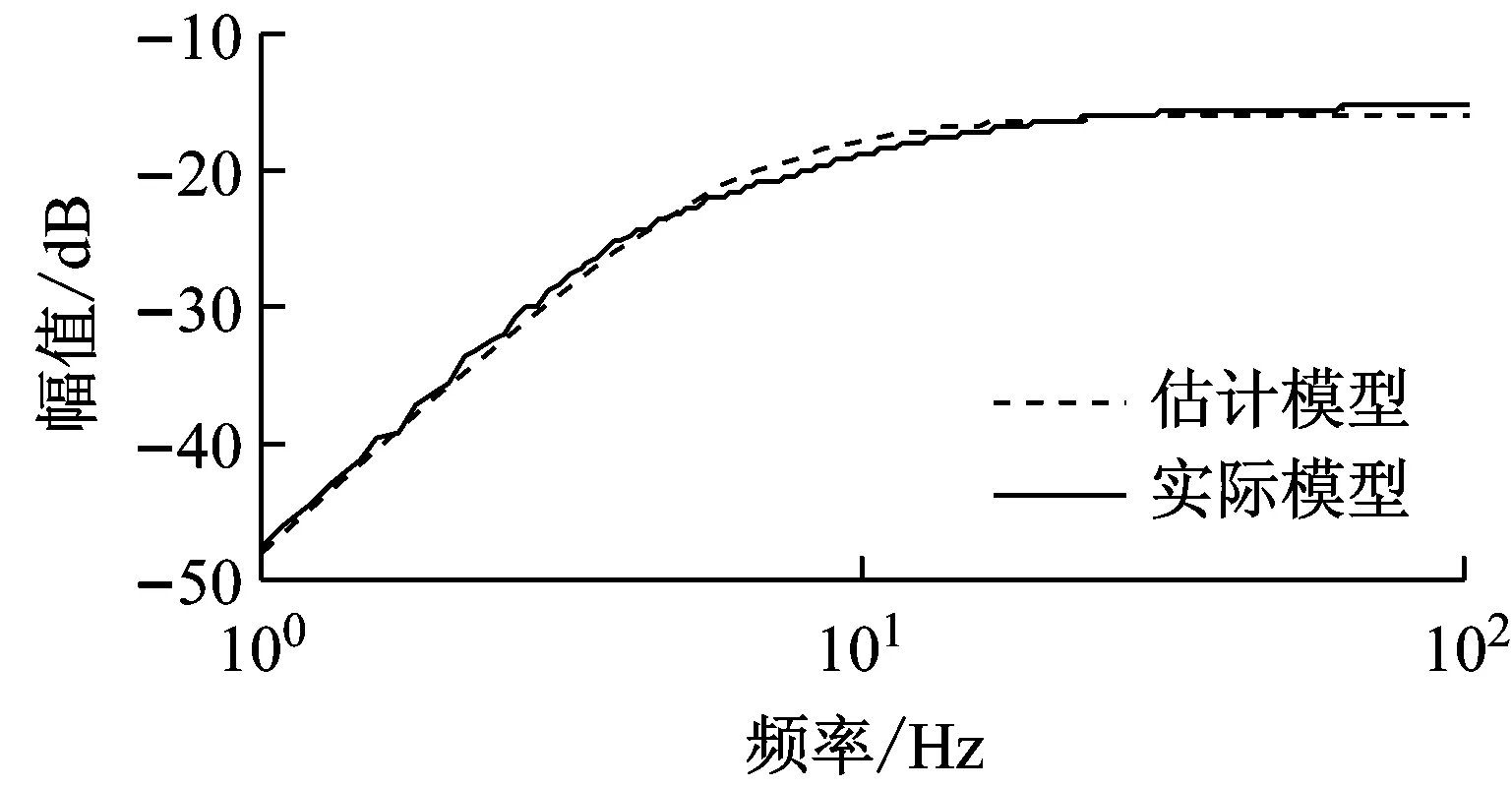
对于控制通道的估计误差，文献[19]指出，控制通道的相位估计误差在±90°内才能保证系统稳定。本文在第3节和第4节分别开展了仿真和实验，在仿真中，控制通道的估计值取式(9)，实际控制通道模型通过辨识Adams动力学模型得到，两者的频率特性对比如图6所示；在实验中，由于实验系统存在约一个采样周期(1 ms)的延时，因此控制通道的估计值需在式(9)的基础上乘以z-1，实际控制通道模型通过辨识实验系统得到，两者的频率特性对比，如图7所示。

(a) 幅频特性

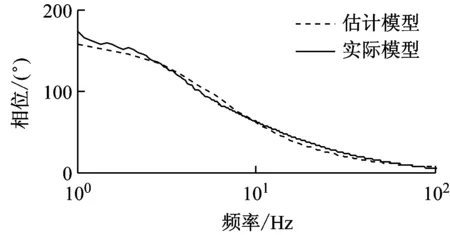
(b) 相频特性图6 仿真控制通道模型对比Fig.6 Comparison of simulation control channel model

(a) 幅频特性

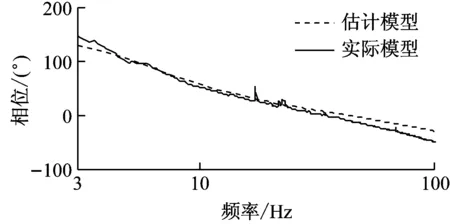
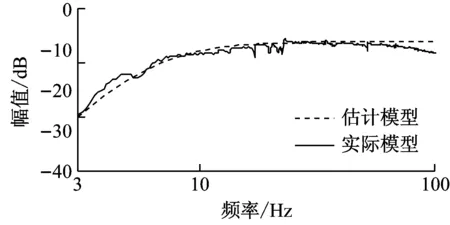
(b) 相频特性图7 实验控制通道模型对比Fig.7 Comparison of experimental control channel model

从图6、7可以看出，仿真和实验中控制通道的估计误差都较小，相位误差在±20°以内，满足相位误差在±90°内的稳定性要求。

对于收敛因子，在控制通道的估计有无误差两种情况下，其取值上限公式有所不同[20]，由于有误差时的上限公式十分复杂，因此在误差较小的情况下，可以先依据无误差时的公式(见式(10))计算上限值，再适当地将该值调小作为真正的上限。

(10)

3 Stewart平台控制仿真

利用Adams和Matlab联合控制仿真检验控制器的有效性。平台的刚柔耦合动力学模型在Adams中建立，其中柔性部件(膜簧和柔性铰链)的有限元模型由Patran建立。控制系统在Matlab/Simulink中搭建。动力学模型如图8所示，FdP_z为上平板X轴上距原点127 mm处受到的沿Z向的直接干扰力，其可同时提供Z向和绕Y向的干扰；AdB_z为下平板中心处受到的沿Z向的干扰加速度。

图8 Adams动力学模型Fig.8 Adams dynamic model

仿真由上、下平板单独受扰和同时受扰三部分组成。上平板单独受扰(抑振)仿真工况：AdB_z=0 mg，FdP_z=1·sin(40πt)N；下平板单独受扰(隔振)仿真工况：FdP_z=0 N，AdB_z=20·sin(20πt)mg；上、下平板同时受扰(隔/抑振协同控制)仿真工况FdP_z=1·sin(40πt)N，AdB_z=20·sin(20πt)mg。

仿真结果分别如图9～11所示，加控后上平板的加速度幅值衰减均在94.3%以上，控制效果显著，初步验证了所设计的控制器在隔振与抑振控制中的有效性。

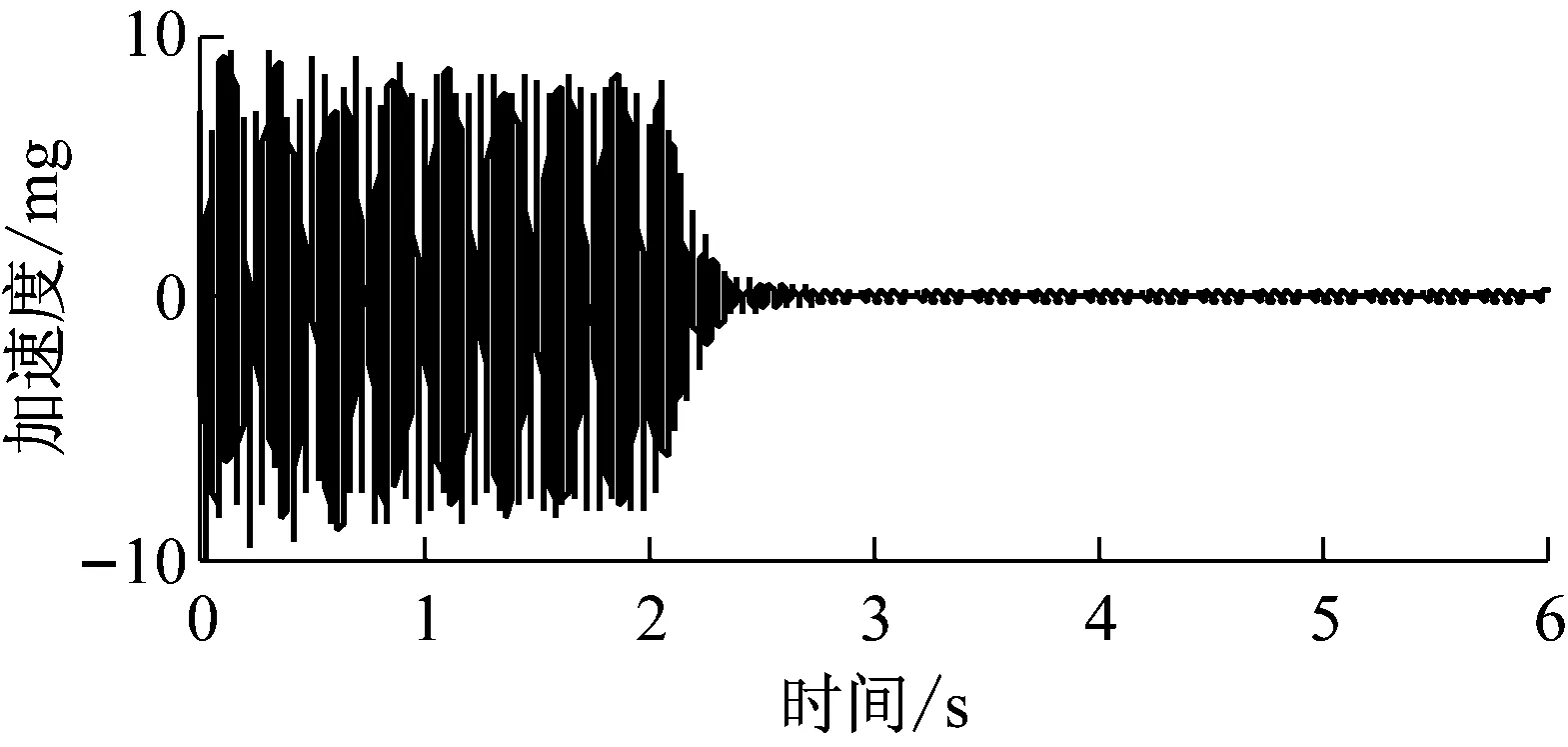
(a) Z方向

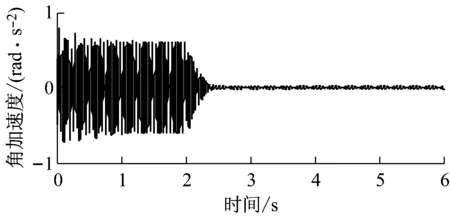
(b) Y转动方向图9 抑振仿真中上平板的加速度响应Fig.9 Acceleration responses of the upper plate in vibration isolation simulation

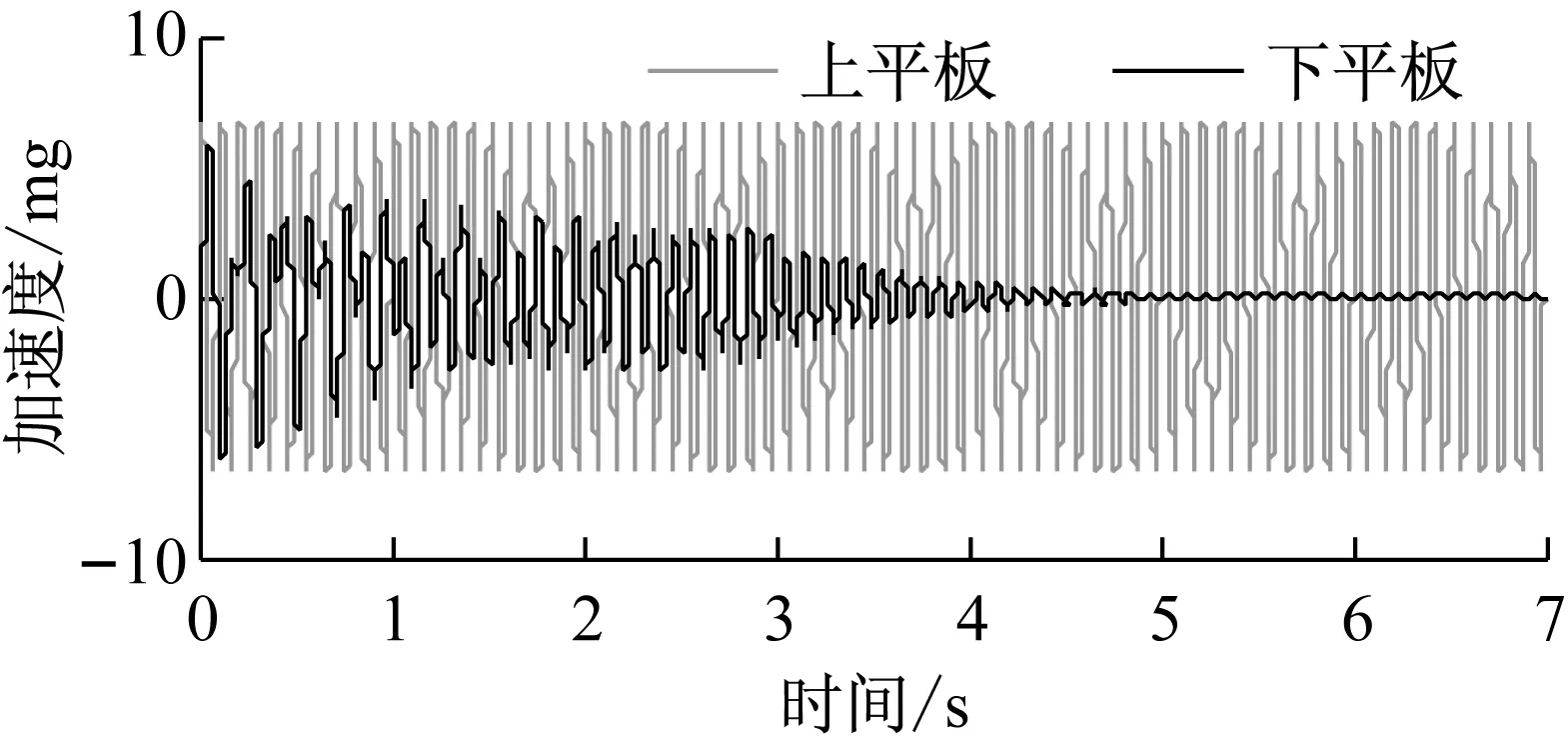
图10 隔振仿真中上、下平板Z向的加速度响应

Fig.10Zdirection acceleration response of the upper plate in vibration isolation simulation

(a) Z方向

(b) Y转动方向图11 隔/抑振仿真中上平板的加速度响应Fig.11 Acceleration responses of the upper plate in vibration isolation/suppression simulation

4 Stewart平台控制实验

实验系统原理如图12所示，主要分为悬吊系统、电控系统和激励系统。悬吊系统包括悬吊弹簧和固定支架，用于抵消上平板受到的重力。电控系统包括9个高分辨率LC0108型单轴加速度计及与其配套的LC0205型信号调理器(加速度计布置情况见图12)、高精度18位PCI-6280型A/D卡、工控机(RTAI实时操作系统)、高精度16位PCI-6733型D/A卡、基于运放器OPA549设计的低噪声高驱动精度的电机驱动器。激励系统包括微振动激励台和JZK-2型号激振器，激励台安装于下平板的下方，可以给下平板施加六个自由度的扰动，激振器固定在下平板上，通过螺杆对上平板X轴上距原点0.127 m处施加沿Z向的干扰力，即同时施加Z向和绕Y向的干扰，实验装置如图13所示。

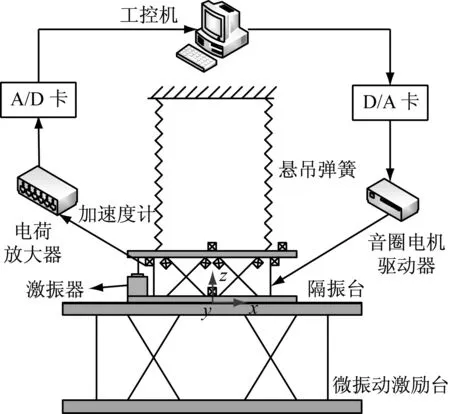
图12 实验系统原理图Fig.12 Schematic diagram of the experimental system

图13 实验系统Fig.13 The experimental system

1) 上平板受定频扰动

工况：下平板固定，激振器对上平板施加幅值约为1.5 N，频率为20 Hz的沿Z向正弦干扰力。

上平板Z方向、绕Y方向的加速度响应如图14所示，加控后，Z向加速度振幅从7.72 mg降到0.70 mg，衰减幅度达到91%；绕Y向的角加速度振幅从0.631 rad/s2降到0.064 rad/s2，衰减幅度达到89.9%，抑振效果良好。

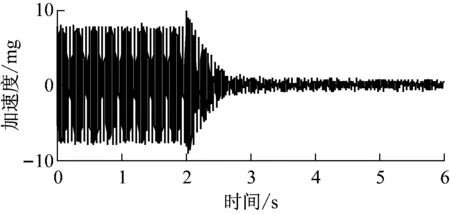
(a) Z方向

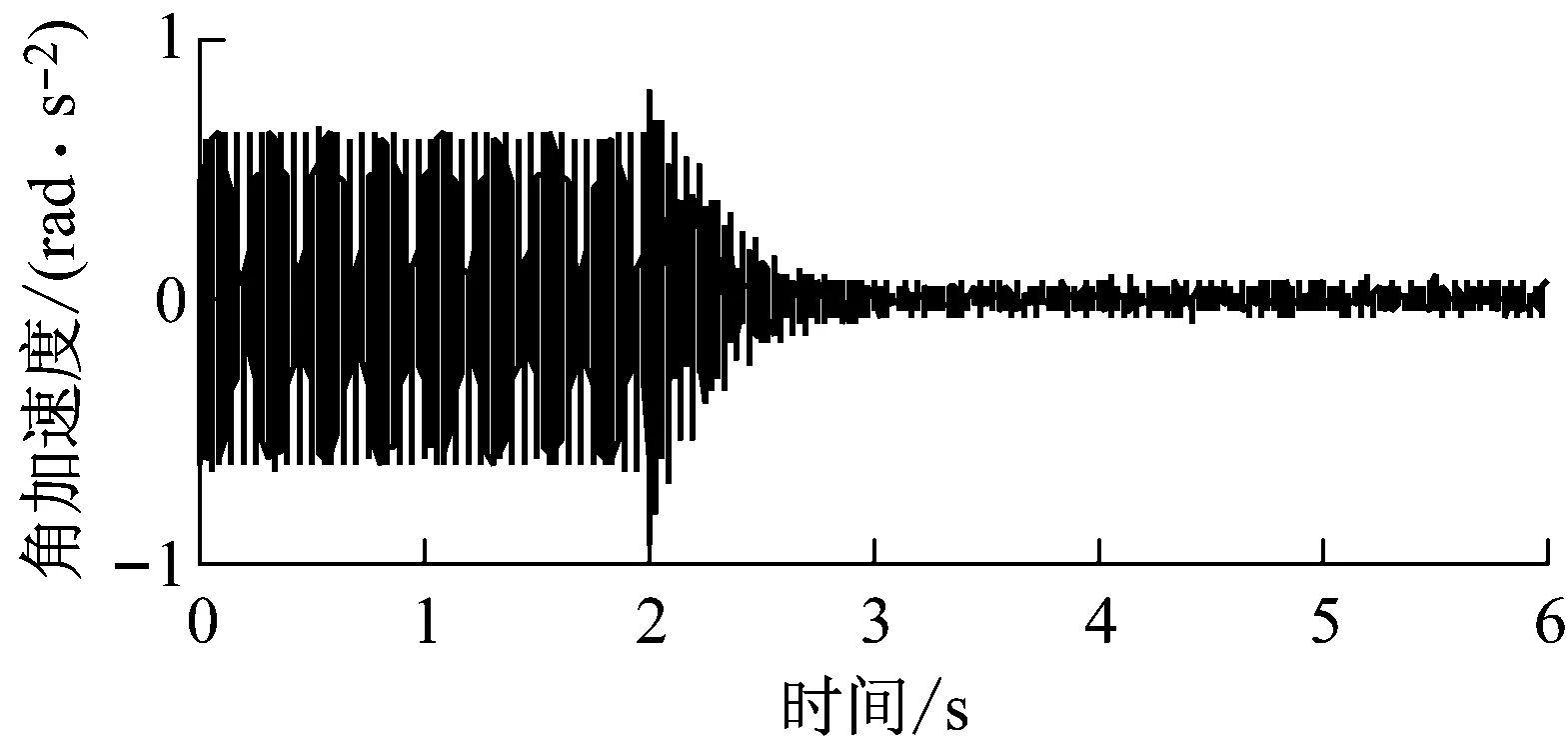
(b) Y转动方向图14 抑振实验中上平板的加速度响应Fig.14 Acceleration responses of the upper plate in vibration suppression experiment

为了验证Skyhook对提高控制系统稳定性的有效性，在相同的工况下，去掉控制器中的Skyhook控制回路，只用自适应滤波进行控制，进行了对比实验。

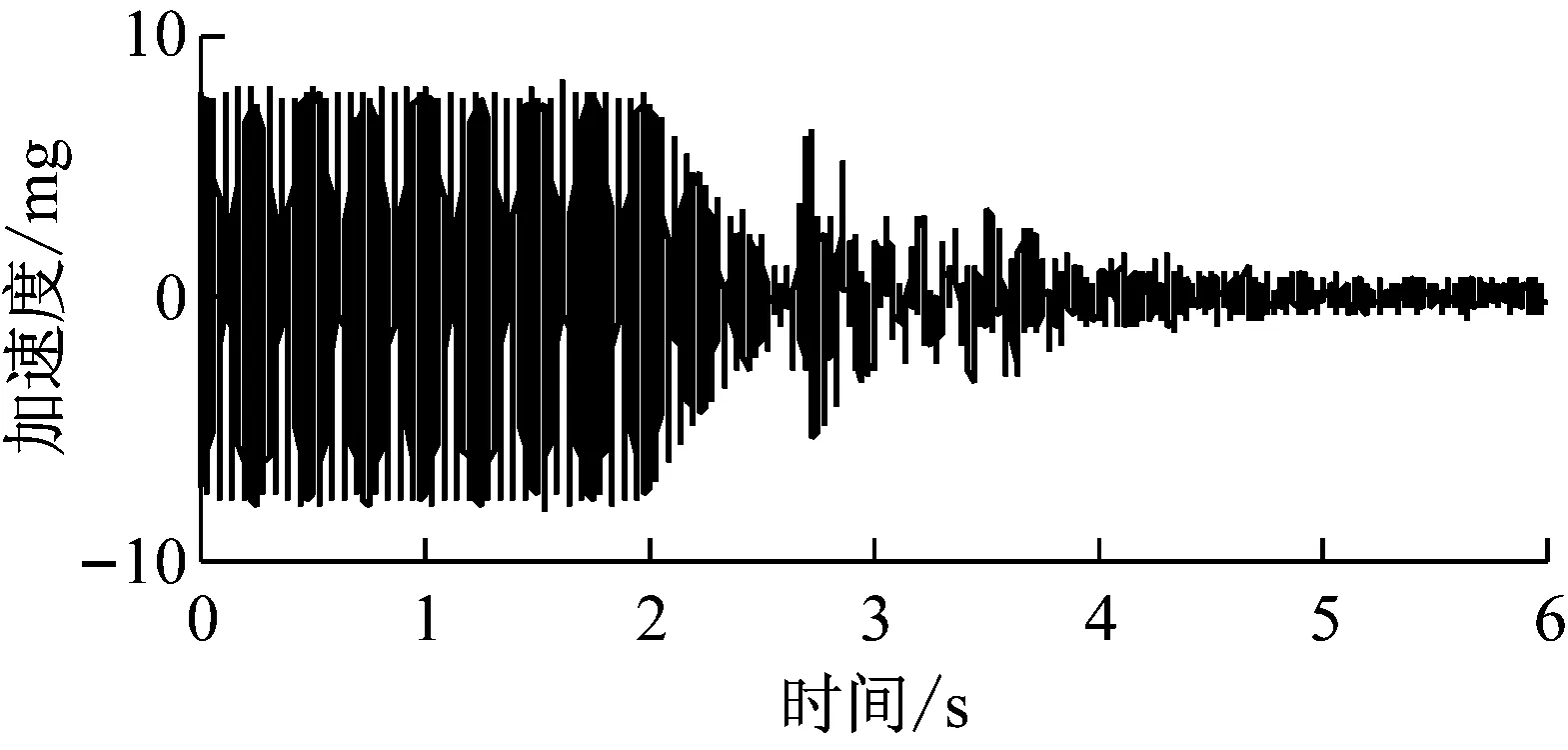
上平板的加速度响应如图15所示，可见收敛过程中存在振荡现象。而图14表明当控制器中存在Skyhook控制回路时，自适应过程十分稳定，两次实验结果的对比验证了引入Skyhook控制回路的有效性。

2) 上平板受扫频扰动

工况：下平板固定，激振器对上平板施加幅值约为1 N，频率为5～100 Hz的干扰力，扫频速率为0.5 Hz/s。

在无控和加控两种情况下，采集上平板的加速度响应，对其进行FFT变换并将幅值单位转换成分贝，得到如图16所示的频域响应。

(a) Z方向

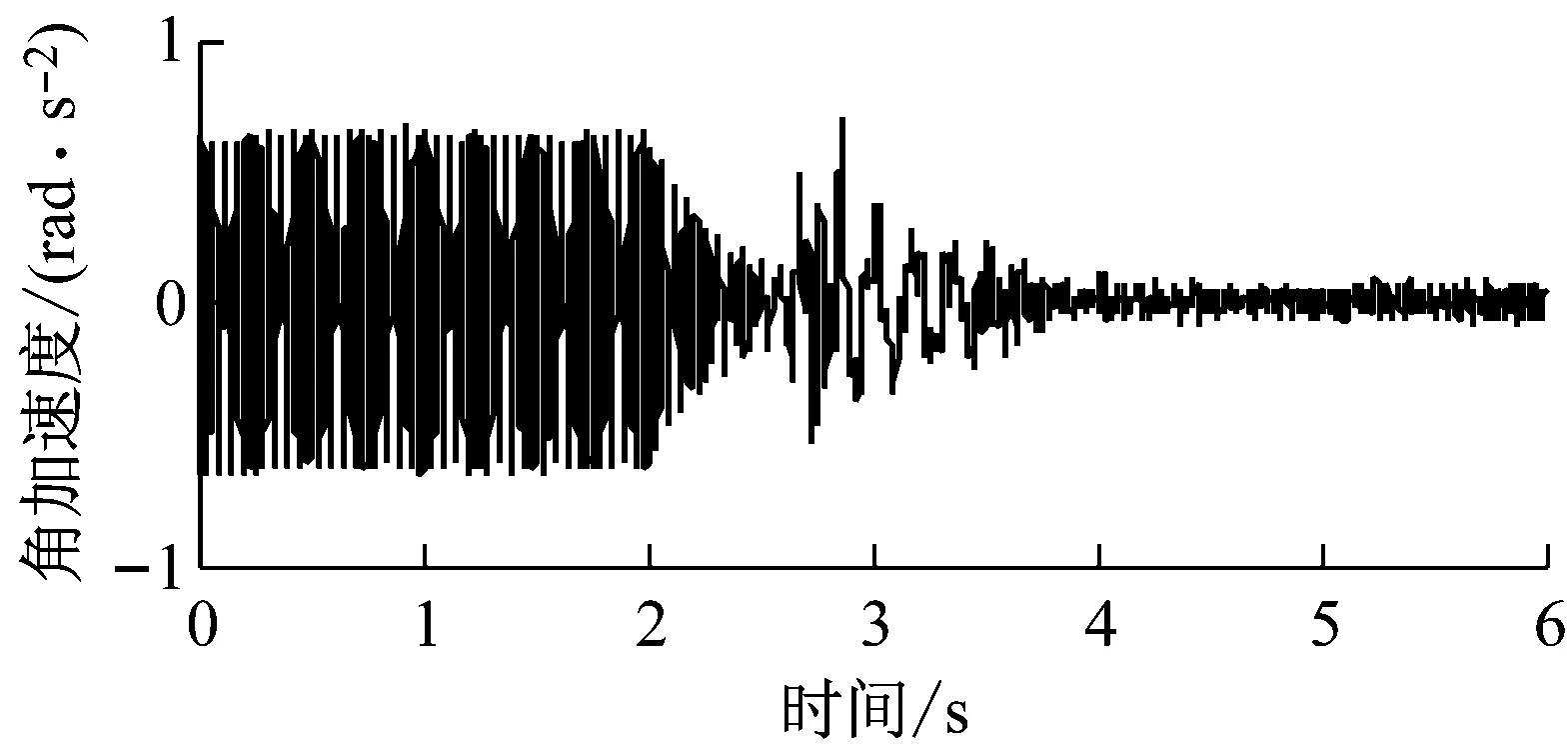
(b) Y转动方向图15 无Skyhook时上平板的加速度响应Fig.15 Acceleration responses of the upper plate without Skyhook

(a) Z方向

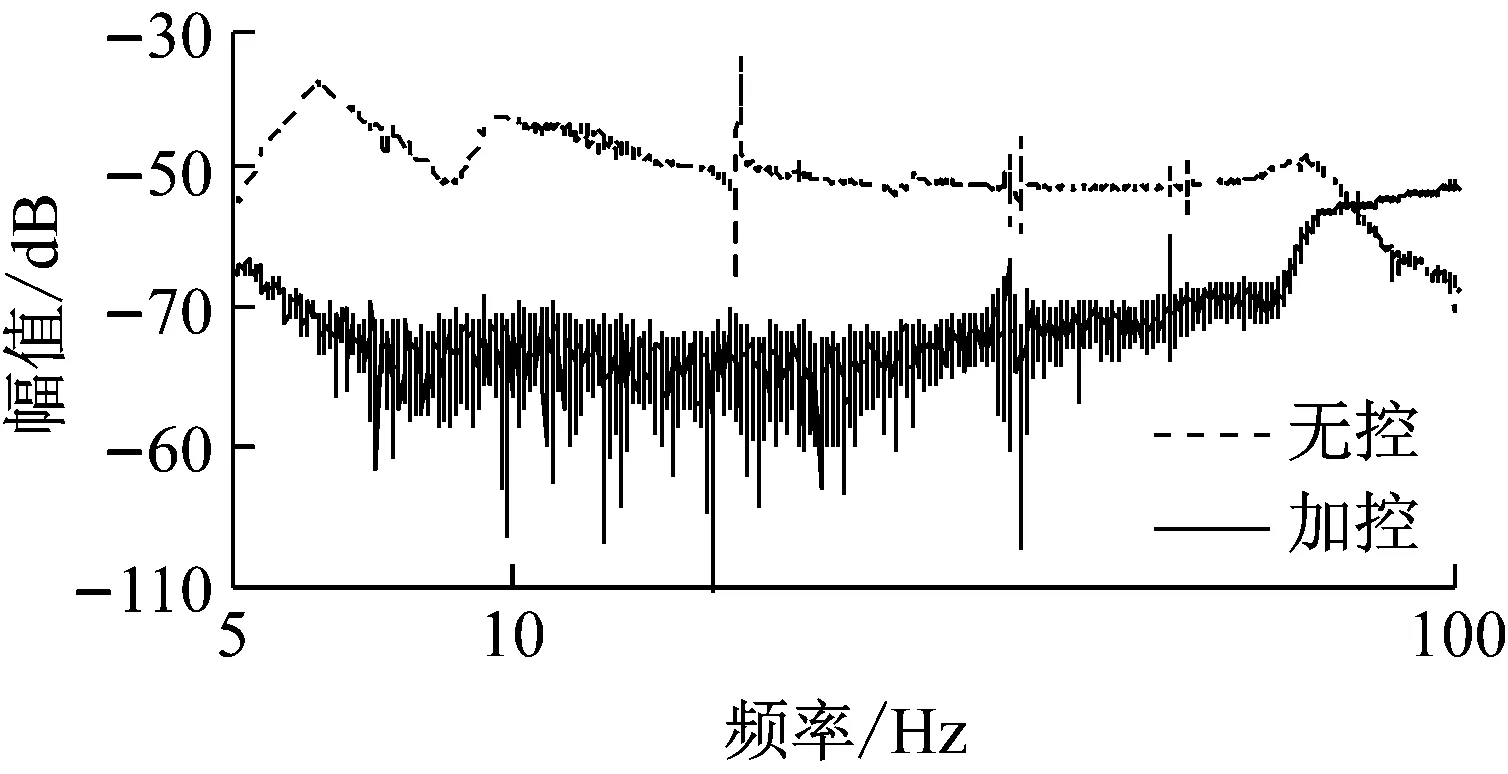
(b) Y转动方向图16 抑振扫频实验中上平板的加速度频域响应Fig.16 Acceleration responses of the upper plate in vibration isolation sine sweep experiment

由图16可以看出，在6～50 Hz频率范围内，加控系统的加速度响应与无控系统相比可衰减至少16 dB，实现了宽带抑振。50 Hz以后控制效果减弱是因为上平板在70 Hz存在柔性模态。17 Hz及其倍频处的共振峰是由悬吊弹簧的自振引起。

3) 下平板受定频扰动

工况：激振器不对上平板施扰，激励台对下平板Z向施加幅值约为20 mg，频率为10 Hz正弦干扰。

上平板Z向的加速度响应如图17所示，2 s时加控，加控后上平板Z向的加速度幅值从6.92 mg减小到0.86 mg，振动传递率相应地从-9.22 dB降到-27.33 dB，隔振效果良好。

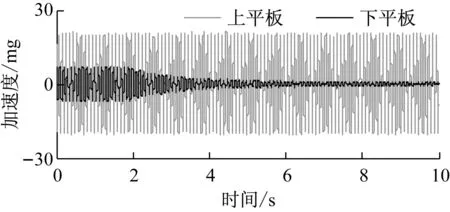
图17 隔振实验中上平板Z向的加速度响应

Fig.17Zdirection acceleration response of the upper plate in vibration isolation experiment

4) 下平板受扫频扰动

工况：激振器不对上平板施扰，激励台对下平板Z向施加频率为5～100 Hz的正弦干扰，扫频速率为0.5 Hz/s，干扰的幅值在5～10 Hz区间内由5 mg线性增加到20 mg，在10～100 Hz区间内保持约20 mg。

因为Skyhook是一种经典的隔振控制方法，所以实验中采用了Skyhook进行对比实验。无控、Skyhook控制以及Skyhook和自适应滤波的复合控制三种情况下Z向的振动传递率曲线，如图18所示。

图18 Z向振动传递率Fig.18 Z direction transmissibility

由图18可以看出，无控系统在5 Hz左右存在共振峰，在18 Hz达到-20 dB的衰减率。Skyhook成功降低了共振频率处的峰值，但在其它频率处的控制效果有限。本文设计的Skyhook和自适应滤波的复合控制使系统在7.3 Hz即可达到-20 dB的衰减率，大幅提高了低频隔振性能，效果优于Skyhook。

在30 Hz以后，无控和复合控制的隔振效果相同，这是因为在30 Hz以后被动隔振已经达到了良好的隔振效果，下平板扰动只会引起很小的杆向加速度响应，因此在自适应律中的死区技术的作用下，自适应滤波方法不工作，避免了不必要的能源消耗。

5) 上、下平板同时受定频扰动

工况：激振器对上平板施加幅值约为1 N，频率为20 Hz的正弦干扰力，同时激励台对下平板Z向施加幅值为1 mg，频率为7 Hz的正弦干扰。

上平板的加速度响应如图19所示，2 s时加控，加控后Z向加速度振幅从8.31 mg降到0.86 mg，振幅衰减达到89.7%；绕Y向的角加速度振幅从0.733 rad/s2降到0.076 rad/s2，振幅衰减达到89.6%。结果表明，当上、下平板同时受到扰动时，控制器仍可以达到显著的控制效果。

(a) Z方向

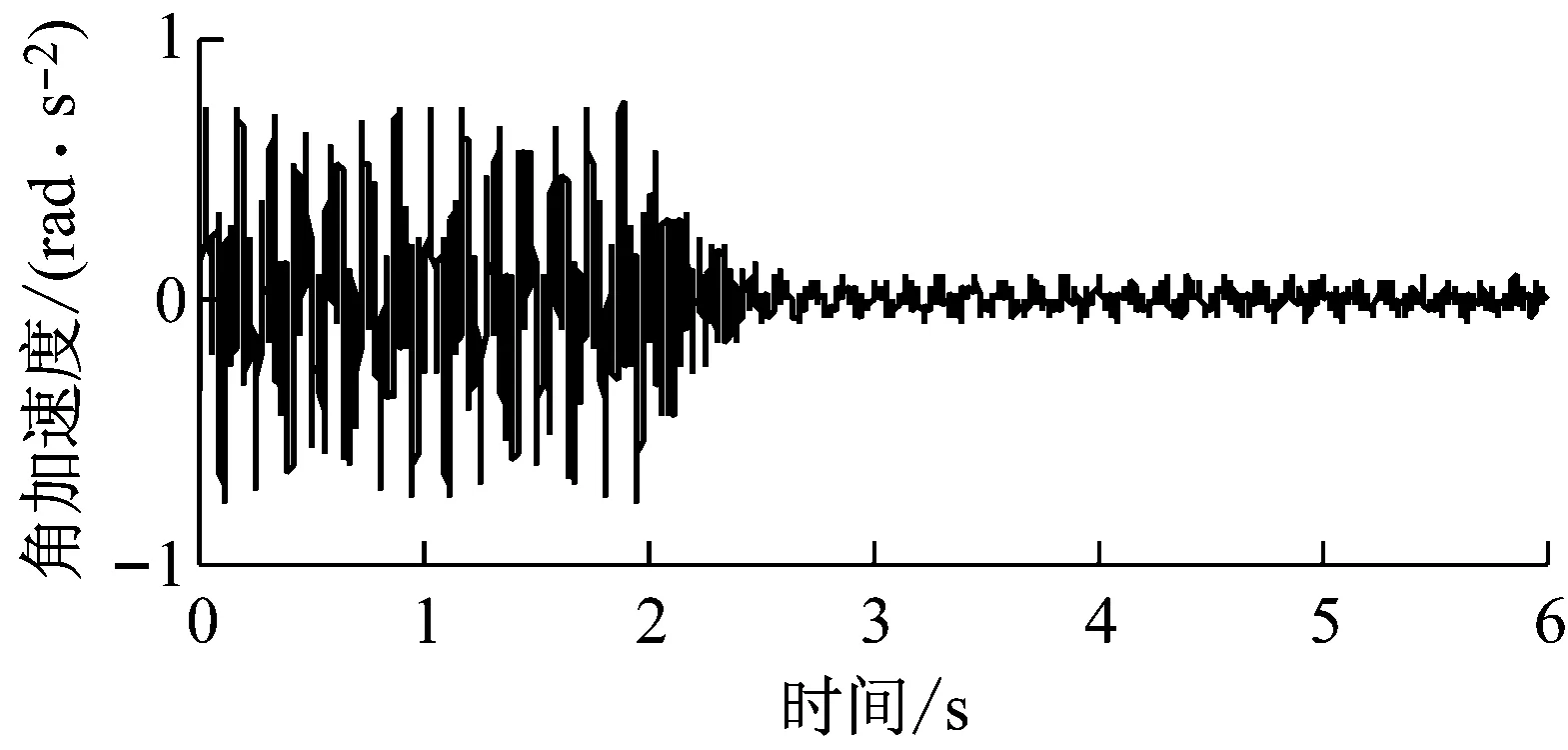
(b) Y转动方向图19 隔/抑振实验中上平板的加速度响应

Fig.19 Acceleration responses of the upper plate in vibration isolation/suppression experiment

6) 上、下平板同时受扫频扰动

工况：激振器对上平板施加幅值约为0.7 N，频率为5～100 Hz的正弦干扰力，扫频速率为0.5 Hz/s，同时激励台对下平板Z方向施加频率为5～100 Hz的正弦干扰，扫频速率为0.5 Hz/s，干扰的幅值在5～10 Hz区间内由1 mg线性增加到10 mg，在30～100 Hz区间内保持约10 mg。

无控和加控下上平板加速度的频域响应,如图20所示。

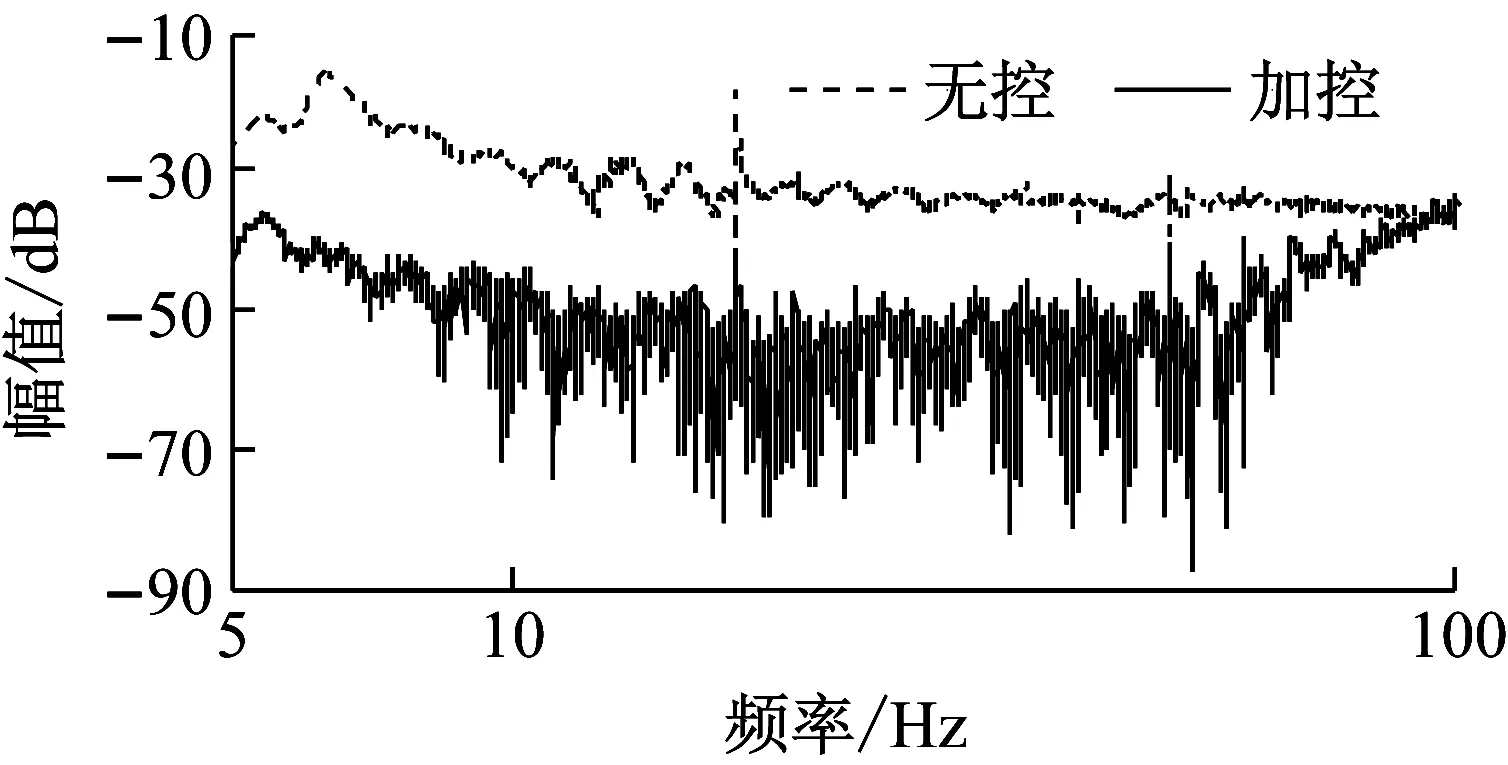
(a) Z方向

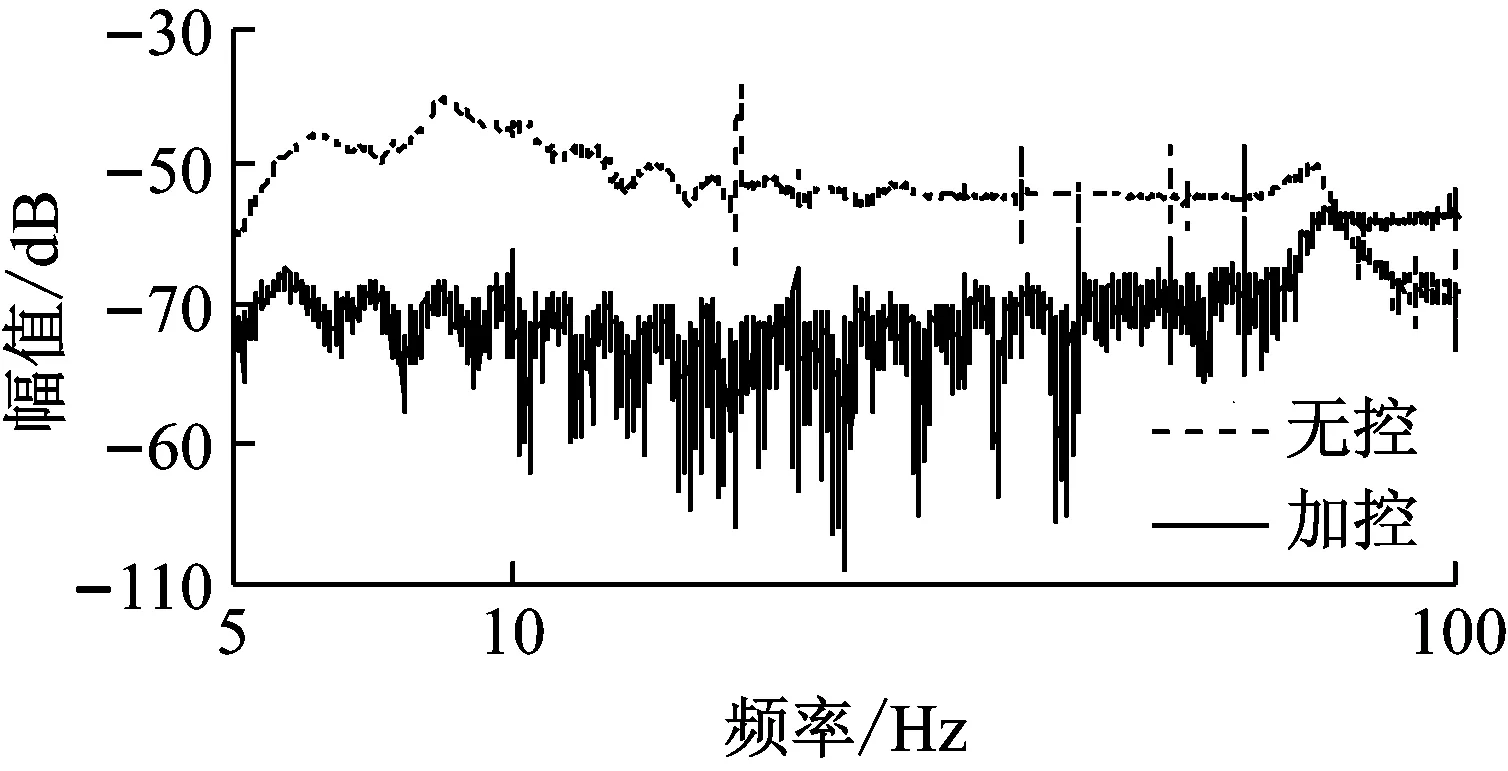
(b) Y转动方向图20 隔/抑振扫频实验中上平板的加速度频域响应

Fig.20 Acceleration responses of the upper plate in vibration isolation/suppression sine sweep experiment

由图20可以看出，在6～50 Hz频率范围内，加控系统的加速度响应与无控系统相比可实现至少12 dB的衰减，进一步表明了本文设计的控制器实现宽带隔振与抑振的能力。

5 结 论

(1) 通过在自适应滤波控制回路的基础上引入增加主动阻尼的Skyhook控制回路，有效地消除了控制通道小阻尼比特性对自适应滤波算法稳定性的不利影响。

(2) 所提出的结合Skyhook的自适应滤波控制方法成功实现了Stewart平台的宽带隔振与抑振协同控制：上平板单独受扰时，平台对于6～50 Hz未知直接干扰引起的扰动可实现16 dB以上的抑制；下平板单独受扰时，-20 dB振动传递率的起始频率由18 Hz减小至7 Hz；上下平板同时受扰时，平台可对6～50 Hz频率范围内的扰动实现12 dB以上的衰减。