基于BP神经网络的FTS输出控制
2019-04-22吕雪军李国平娄军强吕俊智
吕雪军, 李国平, 胡 力, 娄军强, 吕俊智
(宁波大学 机械工程与力学学院, 浙江 宁波 315211)
具有特定微结构表面的光学精密元件在现代光学领域得到了越来越多的应用,光学精密元件的加工需要车刀与主轴的旋转运动保持高频同步,也就意味着切削进给机构必须在提供足够的切削力的同时,具有足够的刚度,尽可能减少加工过程中的振动,保证加工精度,这些要求对于传统的车削设备是无法完成的。为了解决上述难题,近些年快速伺服刀架系统(Fast Tool Servo,FTS[1])的研究逐渐兴起。FTS根据光学精密元件的加工特点,采用频率响应能力高的驱动单元控制刀具的进给等一系列运动,保障具有特定微结构表面的光学精密元件的加工要求[2]。直线电机、电磁执行器和压电陶瓷执行器等常见的驱动单元均可以实现上述功能[3]。根据当前伺服刀架的发展现状,基于压电陶瓷执行器的快速伺服刀架由于其精度高、控制简单等特点得到了较为广泛的应用。国内外对于压电伺服刀架系统[4]的输出位移的精确控制一直都是一个难题。对于该系统,利用传统控制方法很难实现最佳控制,其主要原因是压电伺服刀架系统受驱动器非线性特性、结构特性等因素影响。其次常规比例-积分-微分(Proportional Integral Derivative,PID[5])控制器的参数[6]是固定不变的,无法适应参数变化、干扰等变化因素,对于那些机理较复杂,具有高阶非线性[7]、参数时变性、迟滞[8]等特点的被控对象,难以获得理想的控制效果。只有当参数的变化限定在一定的范围内时,才能够保证系统的工作性能,所以,传统控制方法无法满足上述光学精密元件所提出的高精度加工要求。
针对上文中所提到的传统控制方法的不足,一些学者为了优化快速伺服刀架控制方法,提高控制的精度,对刀架物理特性进行了建模分析,并在模型基础上展开了控制方法研究。Andrew等[9]对其设计的压电型FTS进行了建模和控制算法研究。在建模时,将刀架动力学特性等效为集中参数的单自由度结构,将压电陶瓷的机电传递函数等效为线性比例系数,而迟滞和蠕变特性与切削力共同视为外力扰动,建立了刀架模型微分方程。根据已有的刀架模型微分方程,通过不同算法的对比分析,最终设计总结出滑模控制算法。并且通过相关实验,验证该算法的优点,具有较好的稳定性,可以弱化切削力的作用效果,能将定位误差限制在20 μm之内。但该算法未能有效改善伺服刀架的位移跟踪精度,实验测试结果出现了实际位移曲线滞后于理想位移曲线,且实际的幅值变小的情况。Wu等[10]以音圈电机型FTS为研究对象,开展了相应的建模和控制算法探究。建模时,仍然将刀架的动力学模型简化为集中参数的单自由度结构,将电机的力电关系等效为线性比例系数,得到电压与位移的传递函数。通过建模分析得到该控制系统的传递函数,进行了主动自抗扰算法的研究。通过实验显示,该算法可以实现对于FTS的实时追踪,响应速度快、灵敏度高,但是单纯的主动自抗扰算法精度较差,导致最终误差较大。通过模型前馈处理,可以对其误差进行有效的减少,但仍然接近行程的5%。Wang等[11]设计了一套用于非圆活塞加工的压电型FTS,并采用重复控制的方法来提高控制精度。王海峰将FTS刀架等效为一个单自由度系统,将刀架的电压位移关系等效为一个线性増益,因此刀架的传递函数是一个典型的二阶系统。以二阶系统为理论基础,采用PID控制技术,进行了重复控制算法的研究。通过大量的试验验证,可以发现该算法有效提高了在位移追踪过程中的精度,有效地减小了追踪误差。但是该模型在对于信号的处理过程中,忽略了信号响应延迟对于信号分析的影响。而且由于该模型重复控制的特性,对于以正弦周期信号进行位移控制的FTS具有较为优异的效果,但是,不具备较好的推广性,对于其他类型信号控制的FTS适用性较差。以上几位学者的研究工作从FTS的建模出发,研究其控制算法,取得了不错的成果,但建模分析和控制算法仍然存在一些值得改进的地方,最需要解决的是提高系统模型的准确性,并设计控制精度高的控制算法。
鉴于当前的发展趋势,控制领域的专家学者也对PID控制的改进进行了大量深入的研究,并且取得了一定的研究成果。比如自校正控制、模糊控制等方案。上述改进方法基于各自的理论基础,具有各自独有的优点,但是在具体的改进过程中,均着眼于对于参数选取的改进,并没有对传统的控制器结构进行改进。上述方案相比于现有的PID控制器,得到了一定程度的改进,但是均具有一定的局限性,无法适用于种类繁多的控制问题,使它们的广泛应用受到限制。针对上文中所提到的已有的控制技术的不足,本文采用BP神经网络优化算法[12],提出了一种新型的压电伺服刀架位移输出控制技术。并且根据大量的试验结果显示,该控制技术在实际使用过程中,综合考虑了系统参数变化等问题对于控制效果的影响,可靠性较高。
1 压电伺服刀架的总体设计
通过对上述压电型FTS的分析,得出了机械结构的弹性模量对于刀具的回复力具有重要的影响。上述结构的缺陷主要在于无法提高刀具回复力,导致响应速度较慢。针对上文中所提到的缺陷,本文采用两个压电陶瓷执行器和柔性铰链相结合,通过压电陶瓷执行器为刀具提供回复力,而不仅仅是依赖机械结构本身的弹力,极大的提高了刀具的频率响应速度。同时,该装置采用对称布局的结构,保证了装置的整体刚度。具体设计如图1所示 。

图1 新型FTS模型Fig.1 New FTS model
在上述设计中,压电执行器与柔性铰链的接触面一直处于预紧螺钉的预紧力作用下,保证二者的结合面一直处于贴合的状态。当该装置处于工作状态时,压电执行器A的电压的改变会导致其伸缩长度的改变,继而驱动柔性铰链运动。比如,当电压下降,压电执行器A的伸长量逐渐减小,柔性铰链依靠弹性回复力与压电执行器B的推动力同步产生“收缩”运动。从而实现快速伺服刀架系统所需的伸缩运动。
2 压电伺服刀架系统建模
上文所提及的压电伺服刀架的驱动装置为压电陶瓷执行器[14],由于压电陶瓷执行器的非线性和迟滞特性的影响,定位精度很难达到理想的状态,为了提高刀架的定位精度,必须对压电伺服刀架系统进行控制研究,设计有效的控制器和控制算法。
2.1 压电陶瓷执行器传递函数
压电陶瓷执行器在工作过程中,通过改变其电压,从而改变其厚度。这一特性可以与电容器的充发电过程进行类比。所以可将其当作一个电容和一个电阻的组合,构成一个惯性环节。其简化模型如图2所示。Ui为压电陶瓷执行器的驱动电压,C为压电陶瓷执行器的等效电容,R为等效电阻。
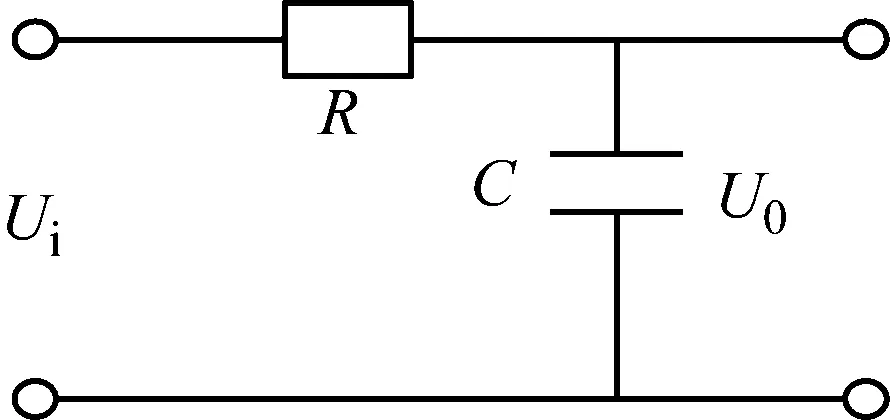
图2 压电陶瓷执行器充放电过程的简化模型Fig.2 Simplified model of charging and discharging process of piezoceramic actuator
根据基尔霍夫定律可得电路的微分方程:
(1)
进行相应变换得:
(2)
当电介质晶体受到电场作用时,会导致形变,继而导致其自身物理特性的改变,这一现象也就是逆压电效应[15],逆压电效应方程表示为:
S=d33E
(3)
式中:S为应变;d33为压电系数(m/v);E为电场强度(v/m)。
联合式(2)和(3)可以得到该执行器的传递函数:
(4)
结合该执行器性能参数,可以得到该压电陶瓷执行器的压电系数d33=0.33,压电陶瓷执行器等效电容C=4.52 μF,等效电阻R=285 Ω。
2.2 压电伺服刀架传递函数
2.2.1 压电伺服刀架传递函数的构建
根据该伺服刀架的运动特点,可以用质量-弹簧-阻尼系统进行类比,具体结构如图3。其中m为伺服刀架的等效质量,k为刀架的等效刚度系数,c为刀架的等效阻尼系数,y(t)为刀架的输出位移,F1(t)为刀架的驱动力,F2(t)为刀架受到的径向切削力。
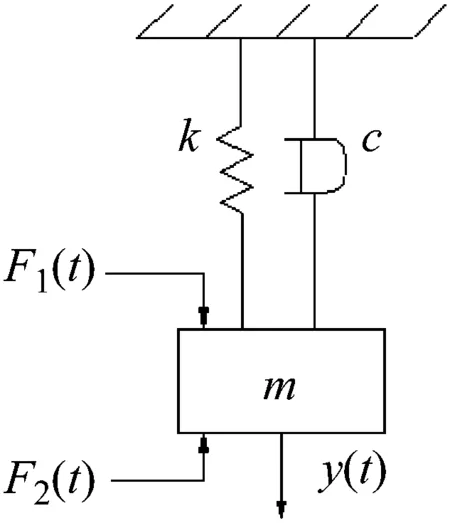
图3 压电伺服刀架动力学模型Fig.3 Dynamic model of piezoelectric servo tool holder
根据牛顿运动定律可得出其微分方程为
(5)
空载情况下F2(t)=0,式(5)简化为,
(6)
对式(6)进行拉式变换,得,

(7)
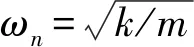
2.2.2 压电伺服刀架传递函数参数的辨识
通过ANSYS进行该刀架的有限元建模,分析得到其刚度k,ωn和ξ可通过压电伺服刀架的频率响应特性测试来获得,最终得到压电伺服刀架动力学模型。
通过Creo2.0进行该刀架的三维建模,采用有限元分析软件对其进行有限元仿真,采用SOLID单元进行网格划分,材料属性为:弹性模量E=68 GPa,泊松比为0.33,密度为2.7 g/cm3,材料的屈服强度为470 MPa。然后分析刀架的刚度,大部分光学精密元件的加工的载荷在1 000 N左右[13],故设置边界载荷为1 000 N,其有限元分析结果,如图4所示。
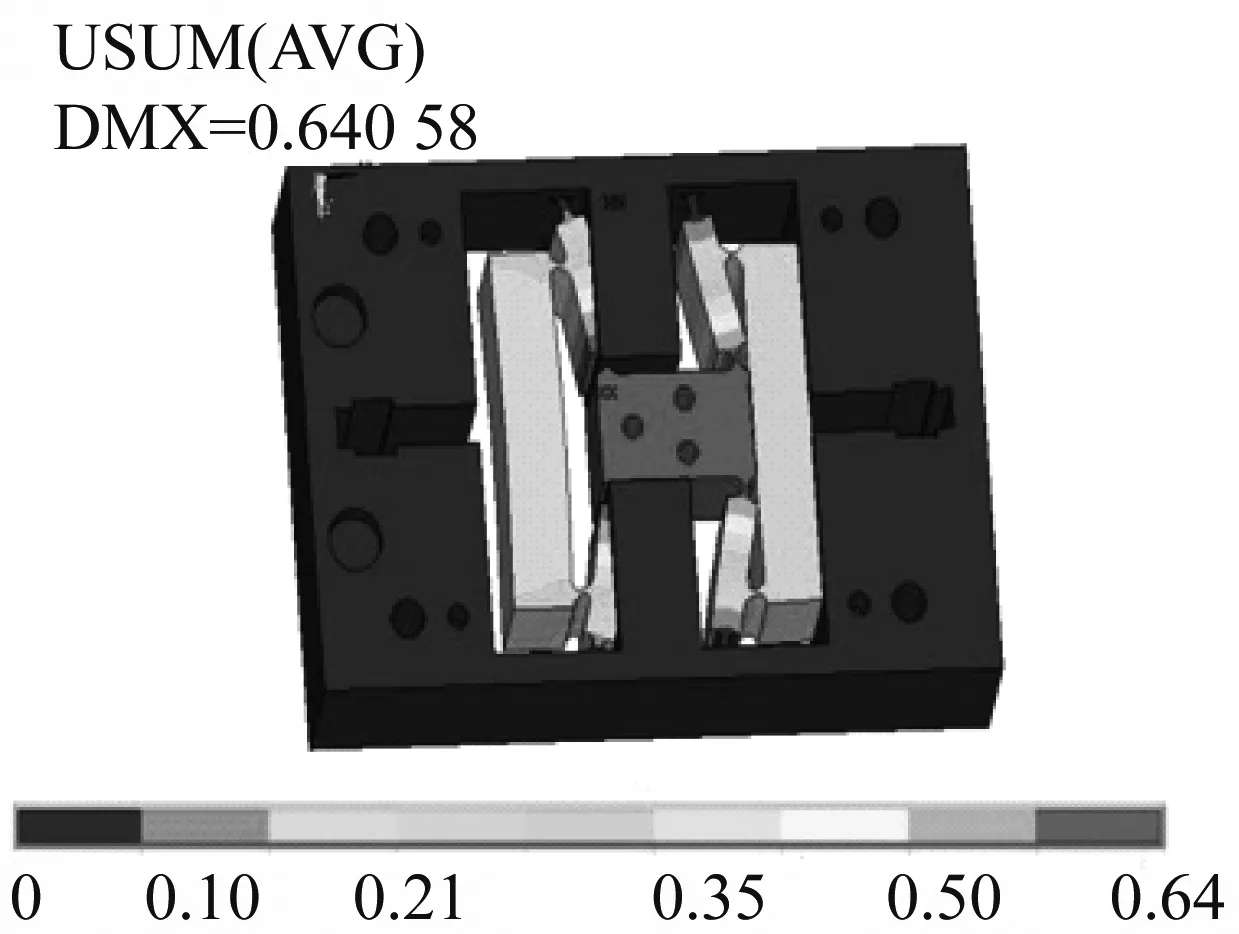
图4 1 000 N时仿真的变形分布图Fig.4 Deformation distribution of simulation at 1 000 N
当刀具获得了大小为1 000 N的外力后,此时可以得出刀具最大输出位移是64.058 μm ,经计算刀具运动部分的刚度为27.427×106N/m。
图5给出了测量压电伺服刀架频率响应特性的实验系统。FFT仪器、脉冲锤和加速度传感器共同组成了测量压电伺服刀架频率响应特性的实验系统。其工作过程是脉冲锤敲打压电伺服刀架使其产生物理上的波动,而这个波动会被敏感的加速度传感器检测到,仪器检测到后会把监测到的波动送入FFT仪器中,最后再经过FFT仪器分析后,得出刀架的频率响应特性曲线。

图5 压电伺服刀架频率响应特性测试系Fig.5 Test system for frequency response characteristics of piezoelectric servo turret
图6给出了基于所搭建系统测得的压电伺服刀架频率响应特性。
根据频谱图半功率带宽法得出阻尼系数:
(8)
Δf=f2-f1
(9)
式中:f和ξ分别表示实际工作过程中压电伺服刀架的固有频率和阻尼系数,f1、f2为在频谱图中共振峰值0.707倍与共振曲线上的两个交点数值。由图6可知共振频率、共振峰值分别是922 Hz和6.342。则f1=843 Hz,f2=952 Hz。将数值代入式(8)可得:
(10)
2.3 压电伺服刀架系统传递函数
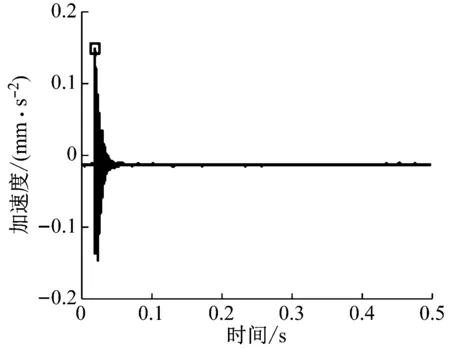
(a) 平台加速度
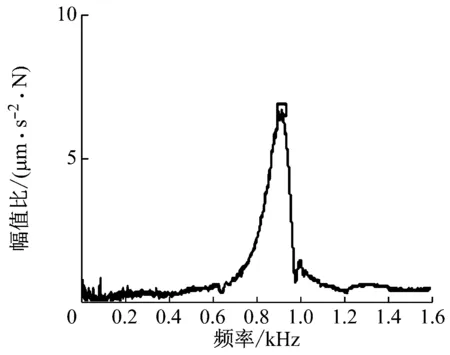
(b) 幅频特性图6 压电伺服刀架的频率响应特性曲线Fig.6 Frequency response characteristic curve of piezoelectric servo tool holder
压电陶瓷执行器的驱动电源实质上是一个功率放大器,把计算机D/A输出的0~5 V电压放大到适用于压电陶瓷执行器的0~150 V电压,其放大倍数为30,因此电源传递函数为:
G3(s)=30
(11)
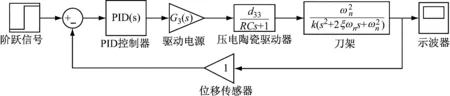
根据各模块的模型,建立整体的开环系统框图,如图7所示。

图7 压电伺服刀架开环系统框图Fig.7 Block diagram of piezoelectric servo turret system
G(s)=G1(s)G2(s)G3(s)=
(12)
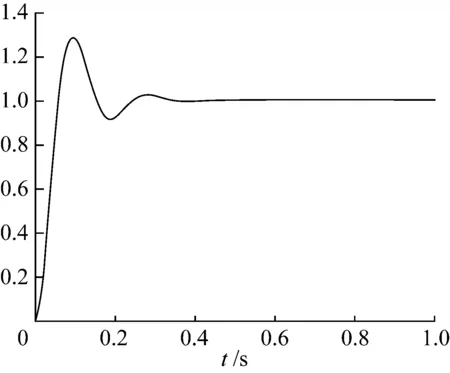
式(12)是压电伺服刀架开环系统的传递函数。通过MATLAB simulink进行仿真,图8是得到的系统单位阶跃响应曲线。
从图12中可以看出,该系统响应时间约为1 s,振荡次数为3次,稳态值为0.009 9,峰值时间为0.144 0 s,超调量为0.497 8。分析数据可得该压电伺服刀架系统的响应时间较长,稳定后的输出值不能准确跟踪输入值,其次,超调量过大,所以必须对该开环系统进行闭环控制,提高其控制精度。
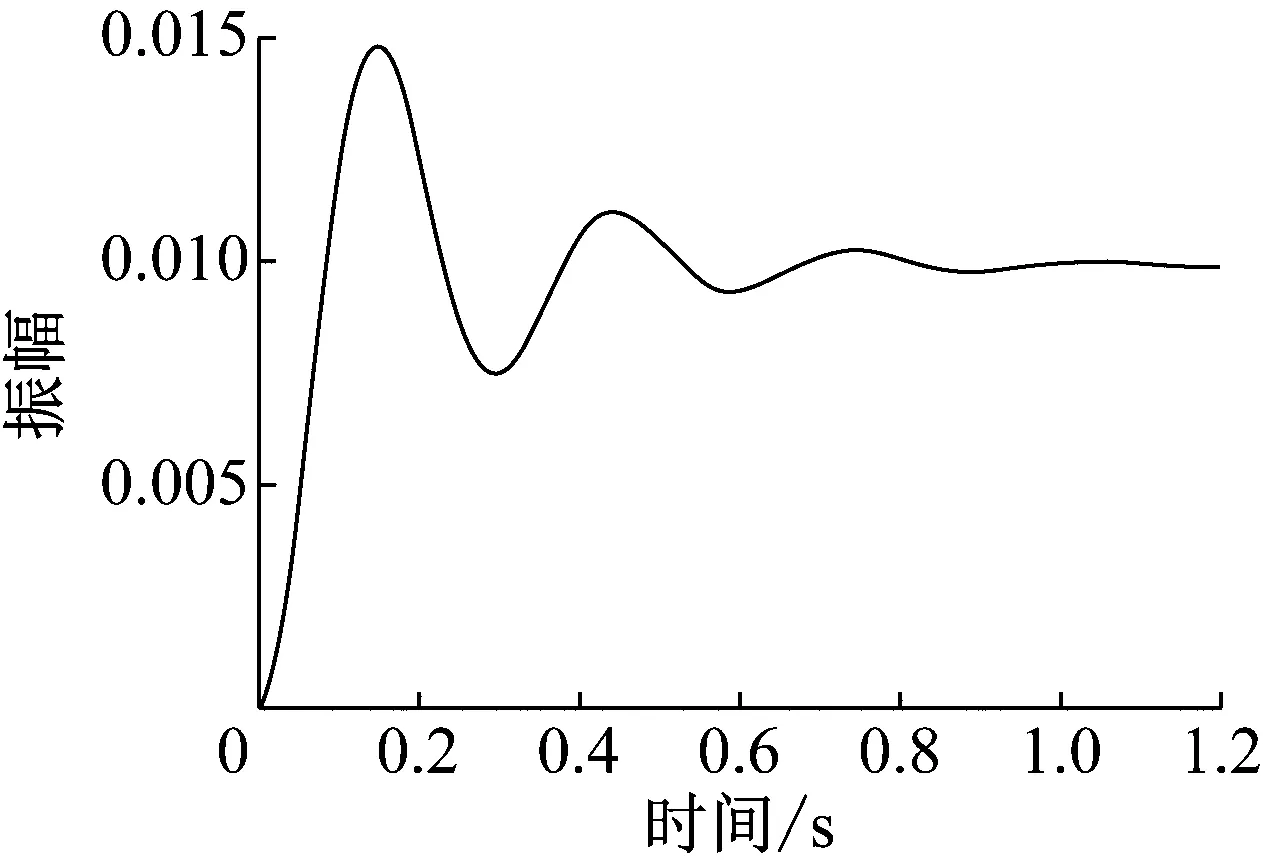
图8 压电伺服刀架开环系统阶跃响应图Fig.8 Step response diagram of open loop system of piezoelectric servo tool holder
3 压电伺服刀架系统前馈控制和PID控制研究
3.1 压电伺服刀架系统的前馈控制器设计
前馈控制属于开环控制,它在模型预测的基础上提前补偿可能出现的偏差,从而及时有效地跟踪被控对象的参考输入。前馈控制需要对所建立的迟滞模型求逆模型。如图9所示,PI迟滞模型及其逆模型在笛卡尔坐标系中关于直线z=r对称,且二者的乘积为单位矩阵E,即z′z=E。
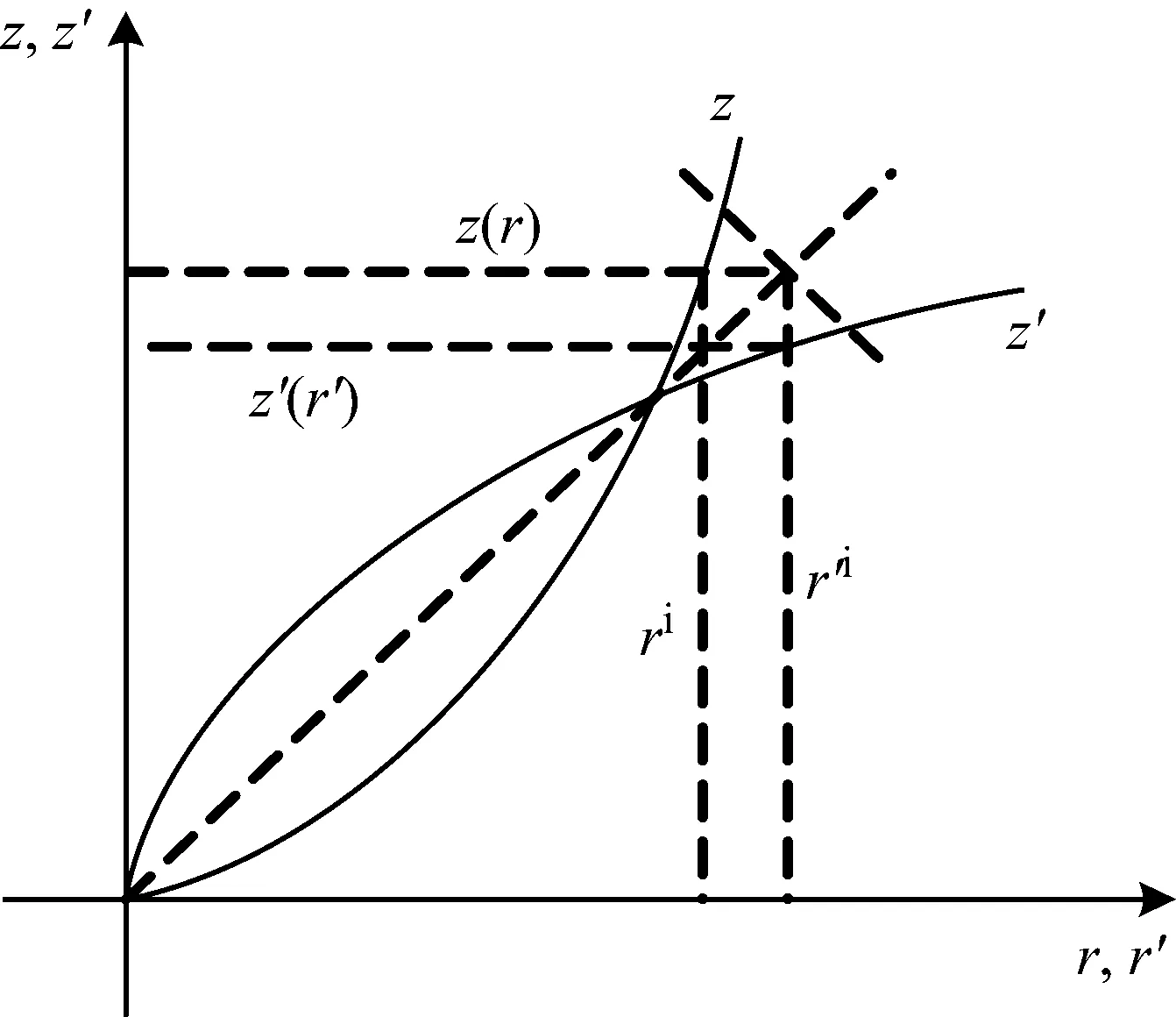
图9 PI模型与其逆模型Fig.9 PI model and its inverse model
由文献[1]可知,PI模型的逆模型为:
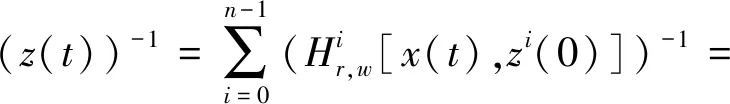
(13)
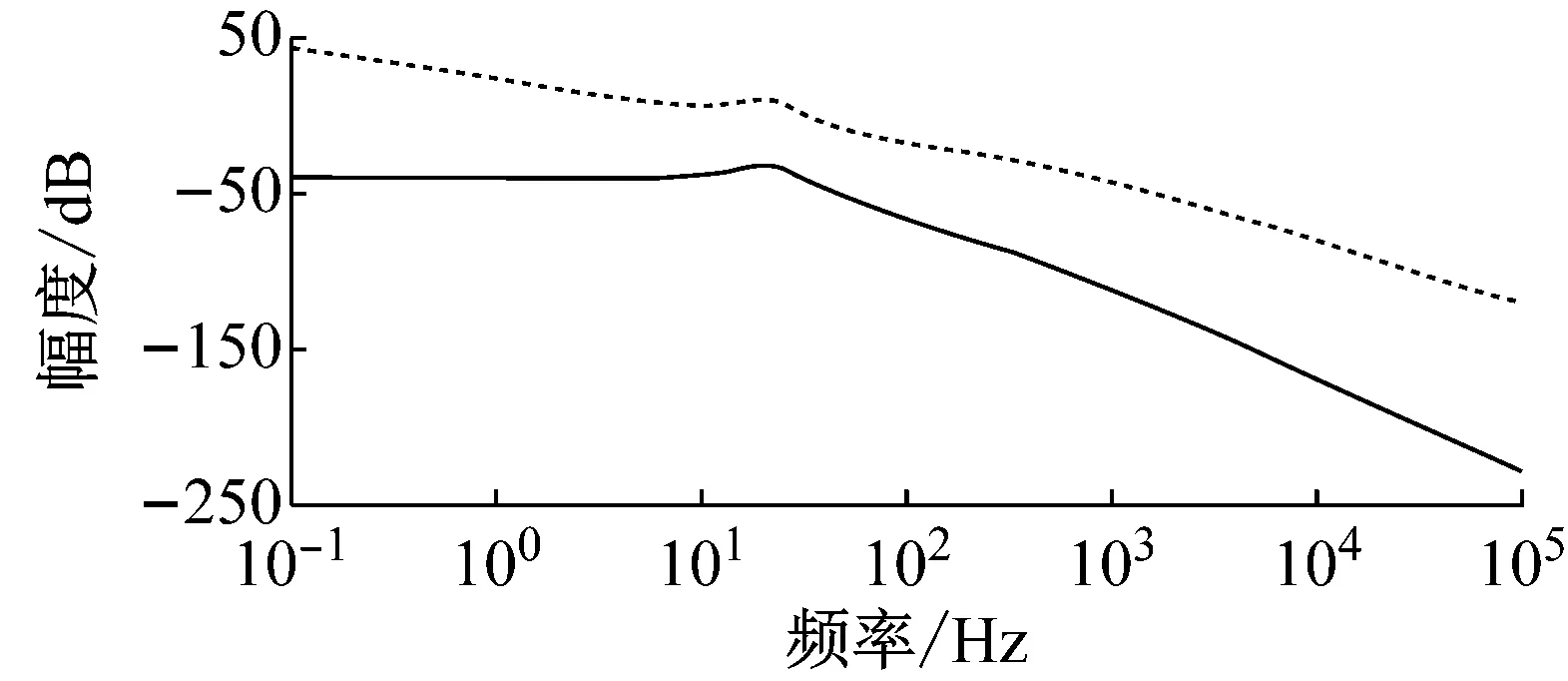
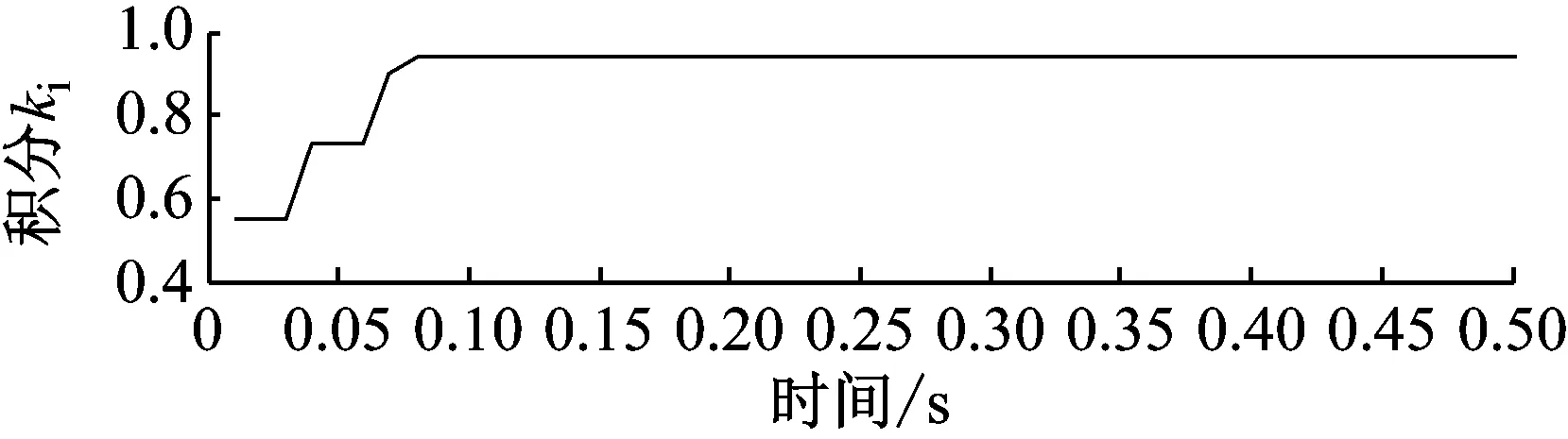
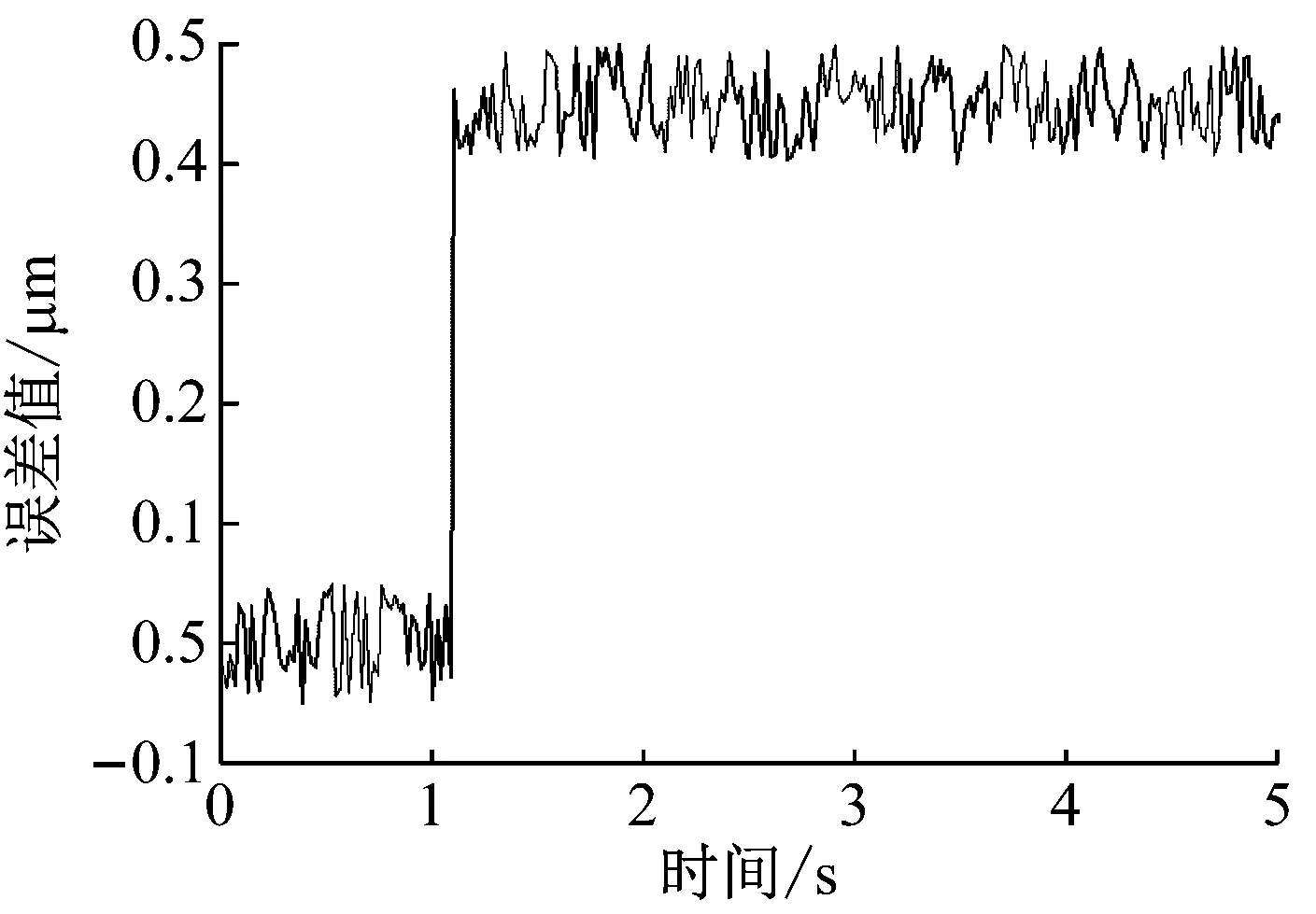
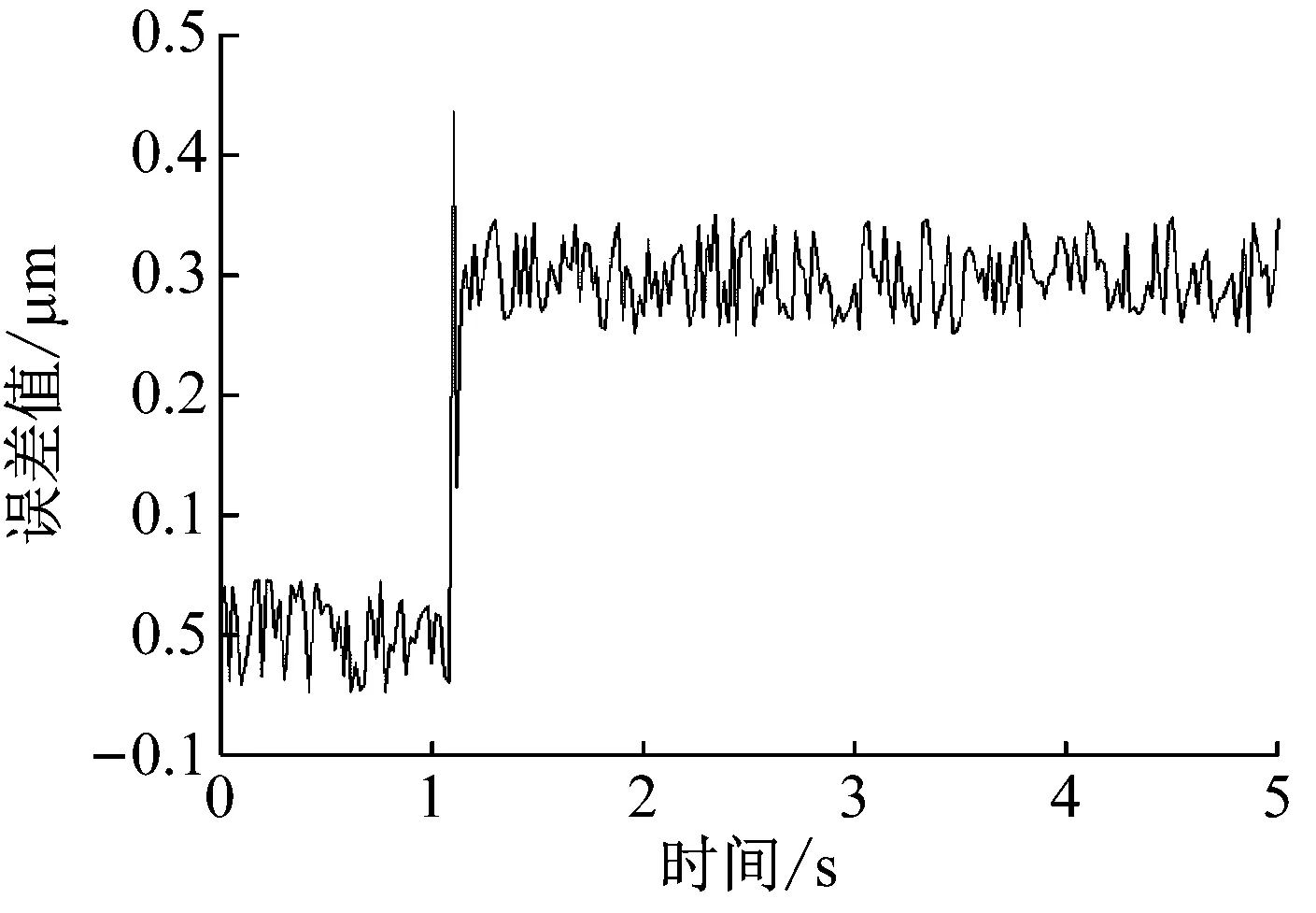
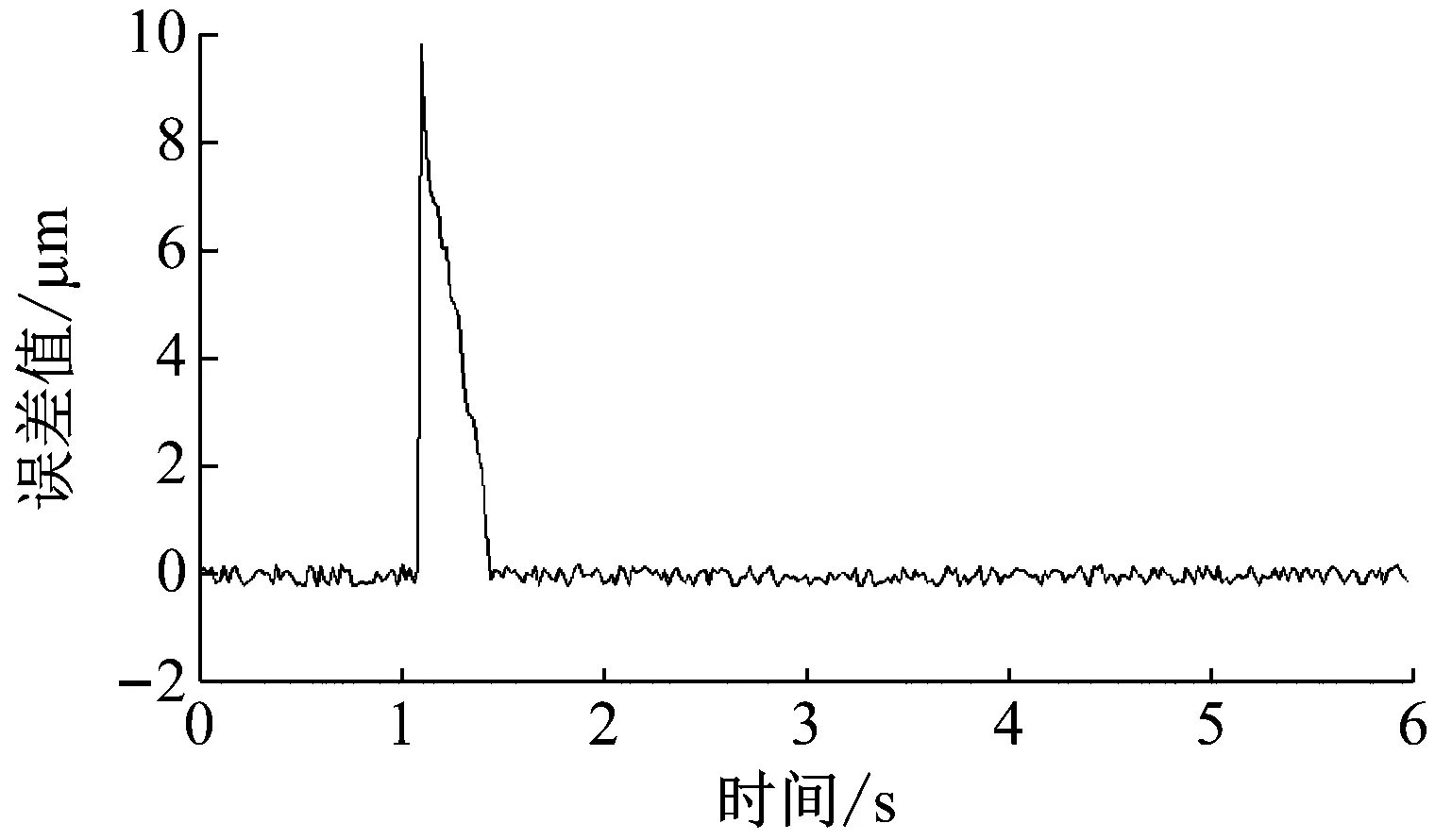
在Backlash算子中,r,w,z,x分别表示阈值、权重、输出和输入。T为采样周期。0=r0 式中, (14) (15) (16) i=1, 2, …,n-1 (17) 将文献[1]中辨识所得到的PI模型参数代入式(14)~式(17),即可求得逆模型的参数,然后将参数代入式(13),从而可得逆模型,即压电伺服刀架系统的前馈控制器。 PID控制算法是由比例、积分和微分三种算法组成的,其中,比例环节调节系统的偏差,积分环节主要提高系统的无差度,微分环节减少调节时间。PID参数整定是PID控制器设计的关键,对控制器的响应速度及控制精度非常重要。本文将采用目前应用较为广泛的Ziegler-Nichols参数整定法[14],达到最优化的参数整定。从而提高压电伺服刀架系统的响应速度及控制精度。 其整定公式如下: (19) 式中:kp,kd和ki分别为比例系数、微分时间常数以及积分时间常数,wm和km分别系统的振荡频率和刚刚产生振荡时的增益大小。在MATLAB 中进行参数整定,得到未整定时开环系统的根轨迹图,如图10所示。在该图上可选定穿越jw轴时的点,从而获得增益km和该点的w值即为wm。 图10 系统整定之前的根轨迹图Fig.10 The root locus diagram of system before tuning 图10和图11分别是整定前闭环系统的根轨迹和整定前后系统的伯特图,在图11中,系统整定后,频带拓宽,相移超前,系统达到完全稳态状态。通过Matlab可求得穿越增益km=164.367 8。采用Ziegler-Nichols整定方法可求得PID参数: 在Matlab环境中建立压电伺服刀架系统PID控制的Simulink仿真模型如图12所示。控制器采用上文提到的PID算法来实现控制。 图11 整定前后系统的伯特图 Fig.11 The Bert diagram of the system before and after the setting 图12 PID控制的Simulink模型Fig.12 Simulink model controlled by PID 图13是PID控制阶跃响应曲线,由图可得大约在经过0.4 s整个系统趋于稳定,不过还具有超调现象,超调量为: (20) 相对于开环系统而言,PID控制在超调量方面改善还是比较明显的,然而在响应时间方面改善不够明显。 图13 PID控制阶跃响应曲线Fig.13 Step response curve of PID control BP神经网络不仅结构和学习算法简单而且具有逼近任意非线性函数的能力[15]。基于神经网络自学习的能力,可得系统最优控制的PID参数。让控制系统的控制参数一直是最优解,可以实现刀架输出位移的高精度控制。图14为以BP神经网络为前提设计出的PID控制系统结构图。 图14中e(k)和u(k)分别是系统实际输出和标准数值的差和控制器的输出。 图14 基于BP神经网络的PID控制系统结构图Fig.14 Structure of PID control system based on BP neural network 该控制器控制算法流程图,如图15所示。 使用MATLAB软件建立神经网络,将学习速率η=0.3,惯性系数设置为α=0.3,加权系数是在[-0.5,0.5]区间内的随机值。初始权值也设置为一个随机数,然后开始运行神经网络,当网络稳定收敛后采用稳定值作为不同层级之前的权值。当我们运行稳定后得到一组新的权值wi,wo如下 图15 BP网络算法流程图Fig.15 Flow chart of BP network algorithm 用该组数据重新仿真得到实时整定参数,控制效果明显得到改善,如图16所示。 图16 稳定权值下BP网络的阶跃响应曲线Fig.16 Step response curve of BP network with stable weights 由图17可得BP神经网络PID控制器性能优秀,在很短时间内就收敛,具有很强的稳定性与适应性。仿真得到的响应结果如表1所示。 表1 控制系统的性能参数Tab.1 Performance parameters of control system 由表1可以得出,BP神经网络PID控制器的最大超调量是一个较小的水平,表明控制效果良好,响应时间仅有0.12 s,这表明系统响应速度快,动态特性良好,可以满足高速响应的要求。 图17 稳定权值下BP网络的参数自适应kp、ki、kd整定曲线 Fig.17 Parameter adaptiveKP,KiandKDsetting curves of BP network with stable weights 压电陶瓷伺服刀架实验平台的组成有五个部分,如图18所示,分别是负责实验平台运算控制的计算机、电涡流位移传感器、负责采集数据的数据采集器、为压电陶瓷执行器提供电源的压电陶瓷驱动电源以及信号调理电路。 图18 压电伺服刀架实验平台Fig.18 Piezoelectric servo tool stand experimental platform 图19给出了在阶跃信号作用下有无前馈控制时压电伺服刀架平台的响应。由该图可知:在10 μm的阶跃信号作用下,图19(a)表示不采用控制措施,刀架平台实际位移与参考位移的最大误差为0.494 1 μm,平均误差为0.363 2 μm,响应时间为0.01 s;图19(b)表示经过前馈控制后,实际位移与参考位移之间的最大误差为0.436 5 μm,平均误差为0.233 1 μm,响应时间为0.01 s。这说明采用控制系统可以显著降低刀架平台的运动误差。 图20表示PID控制系统对刀架平台进行控制后,刀架平台输出位移误差显著降低,仅为0.174 3 μm,响应时间为0.36 s,与前馈控制方式相比,平台运动精度得到了很大程度的提高,但是系统响应时间变慢。 (a) 受控前误差图 (b) 受控后误差图图19 有无前馈控制时平台的误差图Fig.19 The error diagram of platform with or without feedforward control 图20 PID控制下平台的误差图Fig.20 Response and error diagram of platform under PID control 图21是BP神经网络PID控制系统对阶跃输入的响应,可以得到压电刀架平台在经过控制后的输出位移误差为0.112 6 μm,响应时间为0.15 s;相比于前两种控制方式,BP神经网络PID控制在响应时间与控制精度上均有所提高,能够实现高速高精度控制,这可以让刀架平台在短时间内达到很好的定位精度。 图21 BP神经网络PID控制平台的误差图Fig.21 Response and error diagram of platform under BP neural network PID control 本文针对压电伺服刀架系统所存在的迟滞、非线性等问题,首先对压电伺服刀架系统进行了系统建模。运用Ziegler-Nichols参数整定法设计PID控制器,但是单独运用PID 控制器对刀架系统进行控制,虽然可以得到较好的控制精度,但是系统的响应时间较长,为了更好进行控制,需要更为优越的参数整定方法。遗传算法相比Ziegler-Nichols参数整定法更为有效。本文提出了基于BP神经网络的PID控制器,可以实现对PID参数的优化调整,能够实现参数动态寻优,让控制系统的控制参数一直是最优解,可以实现刀架输出位移的高精度控制。通过在MATLAB中进行仿真,可以得出基于BP神经网络的PID控制系统性能优良,系统超调量为25%,响应时间为0.12 s,在保证精度的前提下实现了高速动态响应,并且系统稳定性非常好。基于BP神经网络的PID控制器与传统PID控制以及前馈系统相比,参数整定更为优秀,控制效果也得到了显著提高。实验验证了10 μm的阶跃输入条件下BP神经网络PID控制系统响应时间为0.15 s,与前馈系统相比虽然响应略微滞后,但是控制精度比很高,平均误差仅为0.112 6 μm,这与其他两种方式相比优势显著。3.2 PID控制器设计
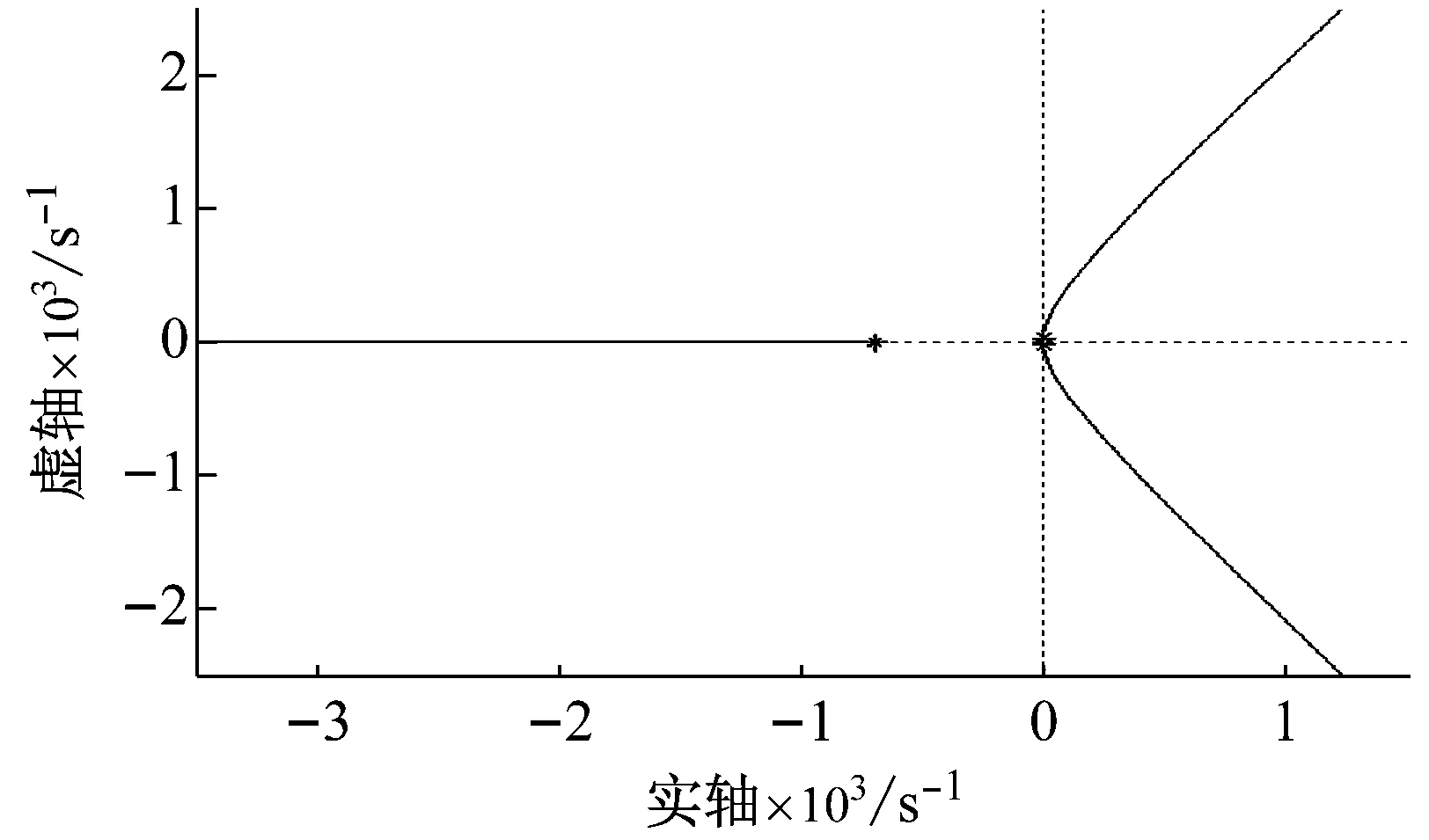
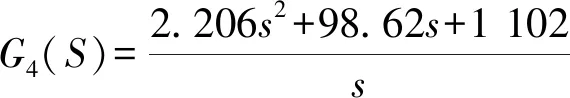
3.3 PID控制器的Simulink仿真
4 基于BP神经网络PID控制器的控制仿真
4.1 BP神经网络的PID 控制器原理


4.2 BP神经网络的PID 控制器在FTS控制系统中的仿真研究



5 实验结果与分析

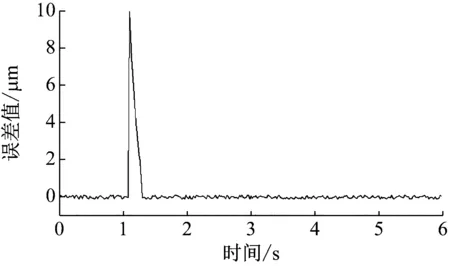
6 结 论
