高速铁路加筋土挡墙土工格栅蠕变损伤本构模型研究

杨广庆， 靳 静,2， 周诗广， 杨国涛， 郑 鸿

(1. 石家庄铁道大学 土木工程学院， 河北 石家庄 050043； 2. 河北科技大学 建筑工程学院， 河北 石家庄 050018；3. 中国铁道学会 标准与认证部， 北京 100844； 4.中国铁路总公司 科技管理部， 北京 100844；5. 青岛旭域土工材料股份有限公司， 山东 青岛 266111)

土工格栅加筋土挡墙因节约用地、加快施工速度、较好抗震性能、外形整体美观等优良的工程特性广泛应用于土木工程、交通运输工程和水利工程等领域。近年来，随着铁路建设的快速发展，铁路路基相关技术规范加大了对加筋土挡墙的应用推广。例如TB 10621—2014《高速铁路设计规范》[1]明确提出“在城市、风景区周边及耕地保护区宜根据现场条件，采用悬臂式、扶壁式、L型及加筋土挡墙等轻型支挡结构。地震区宜采用加筋土挡墙等柔性支挡结构”。TB 10623—2014《城际铁路设计规范》[2]明确提出“在城市、车站、风景区及并行高等级公路等人流密集地段支挡结构宜选用悬臂式、扶壁式、桩板式及加筋土挡墙等支挡结构。地震区宜采用加筋土挡墙等柔性支挡结构”。高速铁路以其快速、安全、准时等技术优势成为现代交通的重要发展方向，加筋土挡墙也成为高速铁路路基的重要组成部分。土工格栅由于具有较高的抗拉强度和抗变形能力而被广泛应用于铁路加筋土挡墙、加筋土挡墙地基处理等加筋加固工程中。然而，在施工和服役期间，由于土工格栅长期处于拉伸状态，而产生的蠕变会影响铁路路基稳定性，因此需要对土工格栅蠕变特性进行系统的研究和分析。由于铁路加筋土挡墙中土工格栅处于不同的环境和应力状态，因而显示出不同的蠕变特性，所以对其在不同温度和荷载水平下的蠕变试验及理论研究可为铁路路基稳定性和变形分析提供理论支持，同时也对预测土工格栅长期力学行为和使用寿命具有重要的意义。

目前，国内外学者对于土工格栅蠕变做了大量的试验研究。Hsieh等[3]采用长期加载法对拉伸塑料土工格栅施加水平拉伸荷载1 000 h后研究其应变的变化。杨果林[4]通过对四种土工合成材料分别施加四种拉伸荷载，历时10 000 h后研究其蠕变性能。丁德斌等[5]通过对土工格栅的一系列蠕变试验，得出荷载大小对土工格栅的流变性具有显著的影响。栾茂田等[6]对土工格栅进行了不同荷载和温度组合下的室内蠕变试验，探讨长期荷载作用下土工格栅的蠕变特性。因为土工格栅蠕变试验要在其控制的环境温度和荷载条件下进行，实验时间一般比较长，超过1 000 h，且费用高。因此，国内外学者们研究出一些能缩短试验时间的方法。Arrag等[7]和Thornton等[8]率先提出了时温叠加法TTS和分级等温法SMI，随后国内学者也开展了土工格栅相关的蠕变加速试验研究[9-10]，试验过程中升高试验温度以缩短试验时间，然后通过温度转换因子，依据高温度短时间内的蠕变等同于低温度长时间内发生的蠕变，从而在相对短的时间内获得长期蠕变特性。

相对于蠕变试验研究，土工格栅本构模型的研究相对比较滞后。目前，土工格栅蠕变试验中应用的本构模型主要有双曲线模型、指数模型和多项式模型等[11-13]，主要描述短时间内的拉伸应力-应变关系，不能满足实际工程的需要。栾茂田[14]、肖成志[15]和周志刚等[16]利用黏弹性理论，提出了土工格栅的三参数经验型蠕变本构模型，并给出了模型中各参数的取值，但是三参数模型只适合于低应力水平下的衰减蠕变模式，不能反应高应力水平下蠕变断裂阶段的塑性变形。周志刚等[17]在三参数模型的基础上提出了黏弹塑性本构模型。以上研究均未考虑温度条件对土工格栅蠕变模型的影响，不能全面反映土工格栅用于路基加筋加固工程时所处的不同温度和不同荷载水平下的蠕变特性。

土工格栅作为一种高分子聚合物材料，在温度和长期荷载作用下材料介质内部微小裂纹会导致材料性能衰减，影响土工结构物的使用和安全性能。因此，描述土工格栅的蠕变行为必须考虑材料本身的损伤特性。目前有关土工格栅蠕变试验主要研究土工格栅的时间荷载效应，有关损伤本构模型的研究相对较少。本文根据不同温度和荷载下土工格栅蠕变试验数据，考虑了蠕变过程中的塑性变形，并结合土工格栅蠕变破坏过程中的损伤演化规律，根据黏弹塑性理论，建立了土工格栅黏弹塑性蠕变损伤本构模型，并对模型中各参数进行了敏感性分析，相关成果对铁路路基加筋土挡墙选择土工格栅提供借鉴。

1 土工格栅蠕变试验

蠕变试验中的土工格栅选用青岛旭域土工材料股份有限公司生产的高密度聚乙烯(HDPE)单向拉伸土工格栅，见图1。该土工格栅由高密度聚乙烯高分子材料经过挤压、冲孔再纵向拉伸而成，在生产过程中高分子通过定向排列而形成分布均匀、具有很高拉伸强度和拉伸模量的网状结构。同时，为提高其耐久性能，在土工格栅中加入炭黑等抗老化材料。为了保障高速铁路加筋土挡墙的安全耐久，根据文献[18]要求，加筋土挡墙需采用HDPE单向拉伸土工格栅，所以本文在不同温度及荷载水平下进行了土工格栅室内蠕变试验。

1.1 蠕变试验

试验所用的土工格栅试样宽度方向保留5根完整肋条，长度方向为1.5 m，土工格栅的基本物理力学指标见表1。在试验温度20 ℃、30 ℃、40 ℃、50 ℃下，施加一定的载荷，按标准规定的时间间隔记录试样的伸长率，直至试样的伸长率超过10%或试样断裂。土工格栅蠕变试验装置，见图2。

表1 土工格栅基本性能指标

试验中，根据强力拉伸试验机测试抗拉强度确定对试样所施加的载荷。不同温度施加的载荷水平见表2，施加荷载以抗拉强度的百分比表示，35%、40%、45%、50%、60%荷载水平对应的测试荷载分别为2 100、2 400、2 700、3 000、3 600 N，蠕变试验总时间约为1 000 h。

表2 土工格栅蠕变试验的荷载水平

1.2 试验结果与分析

通过1 000 h的土工格栅蠕变试验，得到各组土工格栅试验在各温度及荷载组合下的蠕变试验结果，见图3。

由图3可知：(1)在较低荷载水平及较低温度组合下，加载初期蠕变速率线性急剧增加，然后应变速率逐渐减小，直到后期趋于稳定，土工格栅不发生断裂。而在较高荷载水平及较高温度组合下，加载初期蠕变快速增加，而后速率逐渐放缓，直到试样断裂。(2)温度为30 ℃，当蠕变试验加载到200 h，荷载水平为40%、45%、50%时土工格栅的应变分别是8.2%、9.5%、18.6%，这表明在相同温度下，随着荷载水平的增加，相应的应变也明显增大。(3)荷载水平为45%，当蠕变试验加载到200 h，温度为20 ℃、30 ℃、40 ℃、50 ℃时土工格栅的应变分别是8.14%、9.5%、13.5%、21.56%，试验温度50 ℃时土工格栅在大约220 h发生断裂，这也说明温度的升高加快了土工格栅的蠕变断裂过程，为土工格栅蠕变损伤本构模型的建立提供了重要依据。

2 土工格栅蠕变损伤模型的建立

根据不同温度和荷载水平下室内土工格栅蠕变试验结果分析，当试验的载荷水平较小或温度较低时，表现为衰减蠕变模式，即在加载初期土工格栅的蠕变速率比较快，但随后蠕变速率随时间的增加逐渐放缓，最后趋于稳定而不断裂，蠕变应变基本小于10%；随着载荷水平增加或温度的升高，加载初期蠕变也迅速增加，然后蠕变速率逐渐减小而基本趋于稳定不断裂，但蠕变应变会高于10%；当试验的荷载较大或温度较高时(比如20 ℃时施加60%荷载水平或50 ℃时施加45%荷载水平)，蠕变应变随着时间逐渐增大直到试样被拉断裂。

目前，常用的土工格栅三参数蠕变模型为黏弹性模型，由于其未考虑塑性变形，只适合于蠕变应变较小的蠕变曲线，所以三参数模型只能够反映低荷载水平或较低温度下土工格栅衰减模式的发展规律，见图4。为了分析在高荷载(一般高于50%极限应力)或较高温度下(一般高于40 ℃)土工格栅的非衰减蠕变模式，即应变超过10%或蠕变断裂现象，本文提出了一种能够反映土工格栅塑性应变发展模式的本构模型，见图5。其中，三参数蠕变本构模型为Kelvin体和胡克体相互串联而组成的模型，该模型中的关键参数，如黏性系数及弹性模量等适合于蠕变应变较小蠕变曲线。土工格栅作为一种高分子聚合物材料，由于高温、荷载长期作用引起材料损伤，导致土工格栅力学性质劣化直至土工格栅发生蠕变破坏，因此还应考虑在蠕变过程中应力产生的损伤对其造成的影响。因此，考虑细观尺度上的裂纹演化和损伤积累，引入塑性元件考虑土工格栅的塑性应变，该元件采用一个拉伸模量得出应变，用于描述黏性系数的劣化，更适合蠕变应变超过10%的蠕变模式。本文为了能更好的研究土工格栅的蠕变断裂特性，通过损伤力学知识，综合考虑黏弹塑性变形和损伤机制，提出了土工格栅黏弹塑性损伤本构模型。

2.1 考虑塑性变形的土工格栅四参数蠕变模型

四参数蠕变模型是由Kelvin模型与弹性元件和塑性元件串联组成。其中塑性元件用以考虑土工格栅的塑性应变，该元件可以采用一个拉伸模量得出应变。

作为表征土工格栅蠕变的黏弹塑性模型，本构关系为

( 1 )

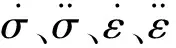
将应力σ=Δ(t)·σ0(t为蠕变时间)代入本构关系式( 1 )中，其中，σ0=4.3 MPa为蠕变试验初始施加的恒定应力，也称为无损时的名义应力，利用拉普拉斯变换及其反演，得到土工格栅无损状态下的蠕变应变为

( 2 )

2.2 考虑损伤的土工格栅黏弹塑性损伤本构模型

土工格栅作为一种高分子聚合物材料，由于高温、荷载长期作用引起材料损伤，通过扫描电子显微镜(SEM)对荷载较大或温度较高时受拉伸的土工格栅进行细观分析，分别在300倍和1 000倍的放大环境下成像，蠕变拉伸引起聚合物内部分子链运动，材料形成丝状聚合物材料，材料内部出现微裂纹，随着丝状分子断裂形成微孔隙结构，见图6。材料细观的微裂纹和微孔洞，会使土工格栅蠕变过程中受荷载的有效面积逐渐减小。

根据损伤力学，Rabotnov提出了损伤因子为[19]

( 3 )

( 4 )

式中：F为蠕变试验施加的外荷载。

利用耦合损伤力学研究土工格栅的蠕变变形时，通过Norton公式得到Kanchanov蠕变损伤因子变化率为[19]

( 5 )

式中：a、n为材料的损伤参数。

由式( 5 )得到蠕变的损伤时间阈值为

tr=[a(1+n)σn]-1

( 6 )

据式( 5 )、式( 6 )得到损伤因子D的演化规律为

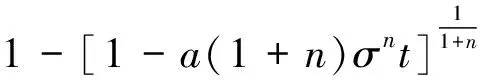
( 7 )

根据Lemaitre的应变等效原理，可以得出损伤土工格栅的变形可以只通过土工格栅本身的有效应力计算。对于任何材料在损伤状态下和无损状态下的本构关系相同，所以损伤材料的本构关系可以通过无损材料的名义应力得到，只需将无损时的名义应力替换为有效应力[19]。将式( 7 )代入式( 4 )并将计算结果再代入式( 2 )中，可得到常应力下土工格栅蠕变损伤的黏弹塑行构方程，即

( 8 )

3 本构模型参数确定及验证

对于土工格栅蠕变的黏弹塑性本构模型式( 8 )中的参数E0、E1、η1、R、a和n，通过建立最小二乘法拟合得到，即

( 9 )

式中：ti、εi为试验过程中蠕变荷载加载的时间、应变；N为试验数据个数。

残差为ri=ε(ti)-εi，目标函数为

(10)

利用Levenberg-Marquardt方法将非线性最小二乘问题变换为求目标函数的最小值问题进行求解，搜索方程为

-JT(zk)r(zk)

(11)

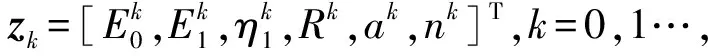
r(zk)=[r1(zk),r2(zk),…，rN(zk)]T

的雅克比矩阵。

通过式(11)对蠕变试验曲线进行参数拟合，得到考虑损伤的土工格栅蠕变模型参数E0、E1、η1、R、a和n，不同温度及荷载组合下的参数见表3。并对蠕变试验曲线和模型拟合曲线进行对比分析，发现两者吻合较好，见图7。

表3 考虑损伤的土工格栅蠕变模型参数

由图7可知：(1)该模型充分考虑时间、荷载和温度对土工格栅蠕变特性的影响，对于不同的温度，在不同荷载水平下的拟合曲线均光滑流畅，且与试验数据契合度较高；(2)采用的耦合损伤黏弹塑性本构模型能够对土工格栅在各种温度和载荷作用下蠕变特性进行较好的描述，可以较好的反映土工格栅在高温度和高荷载水平下的蠕变断裂阶段。

由此验证了考虑塑性变形的四参数蠕变损伤模型的合理性。该模型可以较准确地研究土工格栅在不同温度条件和荷载水平下的蠕变损伤特性，为土工格栅用于各种环境和长期荷载下铁路路基加筋土挡墙工程提供了理论依据。

4 蠕变损伤模型参数敏感性分析

图5建立的土工格栅耦合损伤蠕变本构模型主要由三部分组成：黏弹性体、塑性元件和损伤黏塑性体。黏弹性体中包含参数E0、E1和η1，塑性元件中包含塑性系数R及主要存在于损伤黏塑性体中的损伤参数a、n。为研究土工格栅蠕变参数对土工格栅损伤本构模型中应变的影响规律，对各参数进行敏感性分析。

根据2.1节中的试验条件及表3中的参数拟合结果，取参数E0=46 MPa，E1=17 MPa，η1=590 MPa·s，R=3 520 MPa，a=0.4，n=0.2，σ0=4.3 MPa，代入式( 8 )中，然后通过仅改变其中一个参数，保持其他参数不变，对模型中的各参数进行敏感性分析。

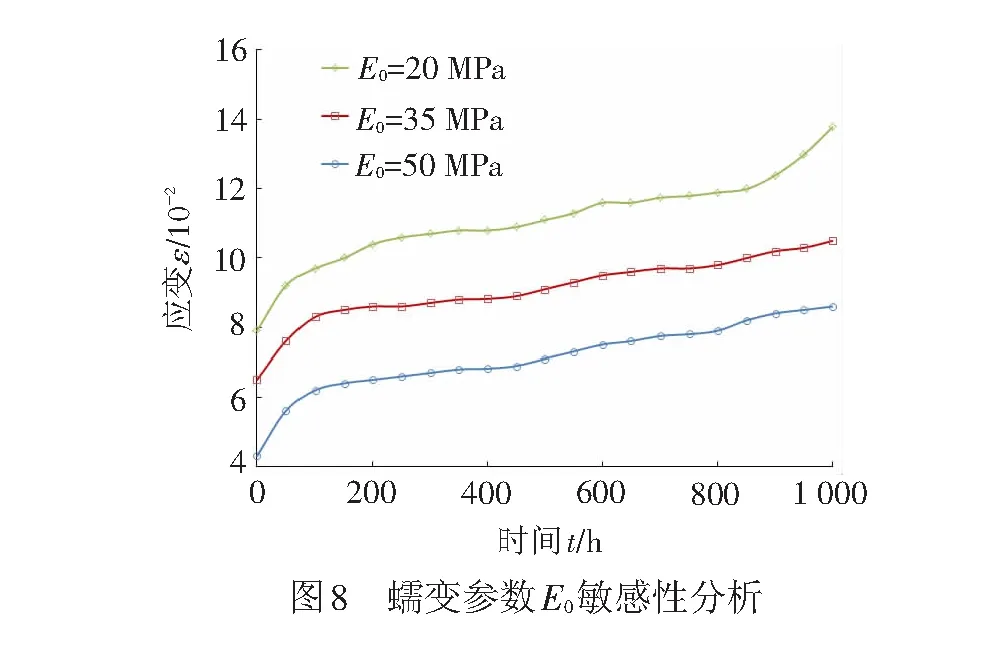
(1) 弹性模量E0的影响

仅改变弹性模量E0的取值，即E0分别取50、35、20 MPa，可得一组不同E0条件下的蠕变曲线，见图8。由此可见，E0的大小直接影响初级瞬态蠕变及整体蠕变应变值，而对蠕变应变趋势、蠕变曲线形状的影响不大。当施加荷载水平相同时，模型反映的初级蠕变及整体蠕变应变随着E0的增大而减小。

(2) 弹性模量E1的影响

保持其他参数不变，E1分别为6、12、18 MPa时的蠕变曲线，见图9。从图9中可以看出，E1对由初始加速蠕变进入恒速的时间及最终的断裂应变值均会产生影响。随着弹性模量E1增加，蠕变过程中进入恒速蠕变阶段的时间越早，最终的蠕变应变也越小。

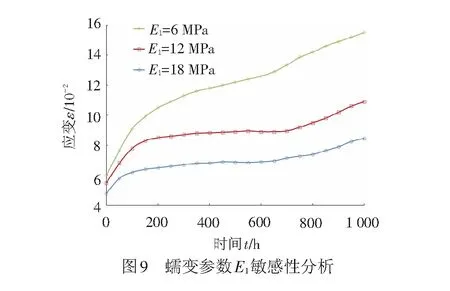
(3) 黏性系数η1的影响

考虑损伤蠕变本构模型中黏性系数η1的影响，保持其他参数不变，改变η1的取值，得土工格栅蠕变曲线随黏性系数η1的变化规律，见图10。可以得出，随着η1的减小，加载初始蠕变率减小，进入恒速蠕变阶段的时间延长。黏性系数η1主要影响初期蠕变变化率，对整体的蠕变应变形成的影响不大。

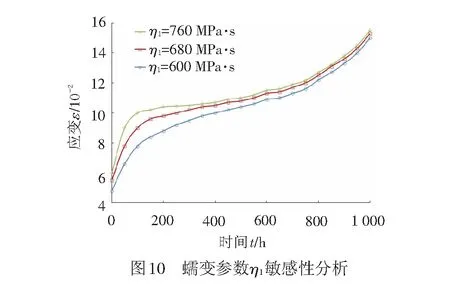
(4) 塑性系数R的影响

不同塑性系数R对本构模型中蠕变应变的影响曲线，见图11。通过比较分析可见，R主要影响恒速蠕变率及最终蠕变量的大小。塑性系数R越小，稳态阶段的蠕变时间越长，最终的蠕变应变越小，但是随着R的增大，加速蠕变断裂阶段较早出现。可以看出塑性参数R的取值对应变及最终蠕变应变大小影响较显著。当塑性参数R较小时，加速蠕变不明显，但随着R的增加，加速蠕变断裂越容易出现。

(5) 材料参数a的影响

耦合损伤的土工格栅蠕变本构模型(式( 8 ))中，考虑损伤参数a的影响，保持其他参数不变，改变a取值，得参数a的影响规律见图12。可见，损伤参数a主要影响蠕变后期的应变增量，当参数a取值较小时，未发生明显的加速蠕变断裂，且随着参数a的增加，加速蠕变断裂阶段越容易出现。

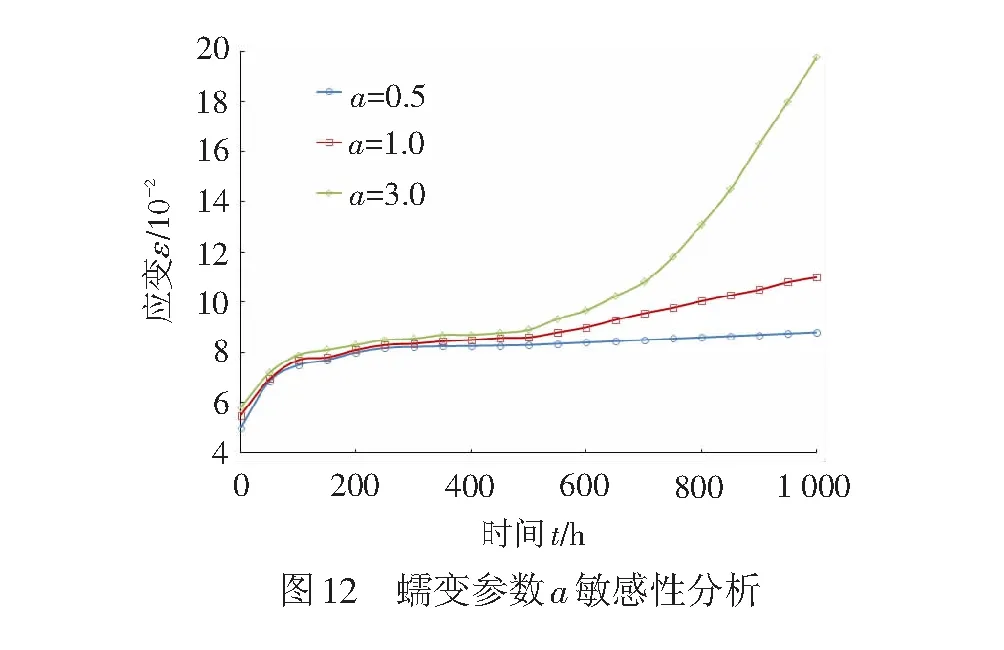
(6) 材料参数n的影响

同样，分析损伤参数n的影响，得到不同n值条件下的蠕变曲线，见图13。通过比较可见，损伤参数n和参数a对蠕变的影响基本一致，参数n取值的增加，更能加速土工格栅的蠕变断裂。

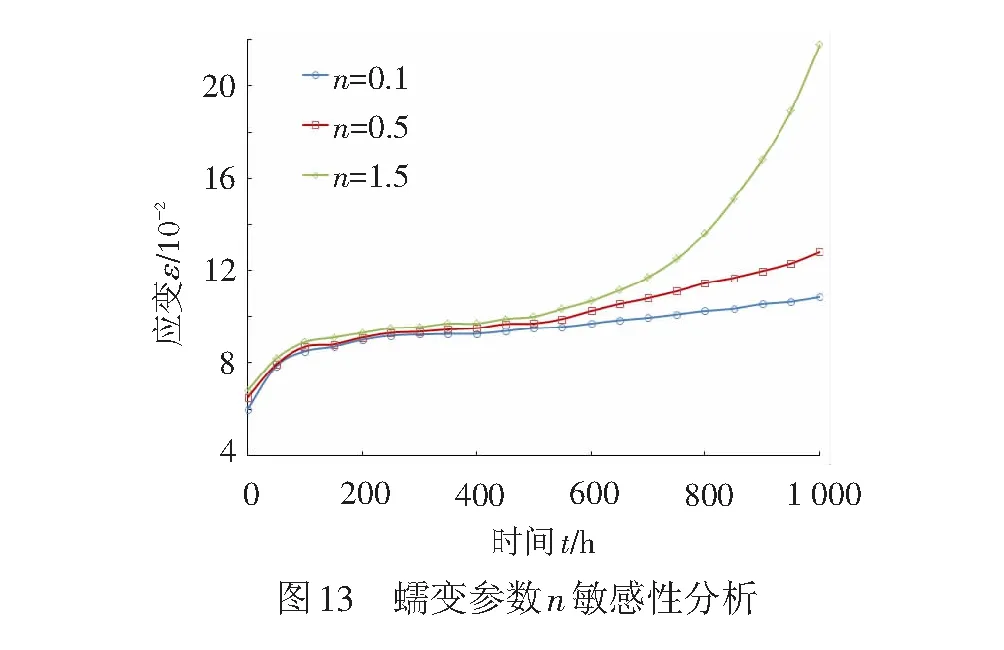
综合上述分析可见，在土工格栅耦合损伤蠕变本构模型(式( 8 ))中，土工格栅的初级蠕变主要受弹性元件中参数E0的影响。黏弹性体中的参数E1和η1主要影响加载初期蠕变速率及进入稳定蠕变阶段的时间，对土工格栅蠕变应变的整体变化趋势影响不大；而加速蠕变断裂主要受损伤黏塑性体中参数R、a和n的影响。可以看出，土工格栅蠕变的加速蠕变断裂阶段受黏弹性体影响较小，主要是通过损伤黏塑性体表现出来。

5 结论

通过对不同温度和荷载水平下室内土工格栅蠕变的分析，得到了土工格栅蠕变损伤受温度条件和荷载水平的影响，构建了土工格栅蠕变损伤黏弹塑性本构模型，并对本构模型中的参数进行了敏感性分析，为铁路加筋土挡墙工程设计与长期工作性能评价提供了重要参考依据。得到以下几点结论：

(1) 不同温度(20 ℃、30 ℃、40 ℃、50 ℃)和不同荷载水平(35%、40%、45%、50%、60%)条件下，土工格栅的蠕变特性试验结果表明，土工格栅的蠕变全过程分为：加载初期蠕变快速增加阶段、稳定蠕变阶段和蠕变断裂阶段。温度和施加荷载条件对土工格栅的蠕变速率和损伤积累形成的断裂均有显著影响。

(2) 考虑土工格栅在不同温度及荷载作用下蠕变过程中的损伤累积对土工格栅材料特性的影响，在三参数模型的基础上，引入了一个塑性元件，并结合损伤力学的理论，构建了耦合损伤的土工格栅黏弹塑性本构模型。

(3) 土工格栅蠕变损伤本构模型可以比较准确地描述不同温度和荷载水平下土工格栅蠕变全过程。通过对土工格栅蠕变损伤模型和试验结果的对比分析，两者吻合度较好，验证了土工格栅的黏弹塑性损伤本构模型能够较合理地反映土工格栅的蠕变损伤特性。

(4) 通过分析土工格栅损伤蠕变模型中各参数对土工格栅蠕变变形的影响规律，可以得到，塑性系数R和材料参数a、n对土工格栅蠕变的影响比较显著，随着R、n的增加，土工格栅的恒速蠕变阶段时间越短，加速蠕变断裂越容易发生。