波浪、海流环境中跨海桥梁深水桥墩的地震响应特性

2019-04-22白晓宇孟宪锋杨庆山

铁道学报 2019年3期

江辉，白晓宇，黄磊，李辰，孟宪锋，杨庆山

(1. 北京交通大学土木建筑工程学院，北京 100044； 2. 中国民航机场建设集团有限公司，北京 100101；3. 重庆大学土木工程学院，重庆 400045)

随着“一带一路”、“长江经济带”及“西部大开发”等重大发展战略持续推进，加速了骨干通道和综合立体交通走廊的建设，使得深水桥梁的建设需求日益旺盛。跨海桥梁作为深水桥梁的重要类别之一，其建设如火如荼，如已建成的胶州湾跨海大桥、杭州湾跨海大桥、东海大桥、港珠澳跨海大桥等，在建的跨越活动断层的海南铺前跨海大桥、平潭海峡公铁两用大桥、大连湾跨海交通工程等。此外，已进入可行性建设方案论证阶段的琼州海峡公铁两用跨海大桥[1]，以及处于前期探索和研究阶段的渤海海峡、台湾海峡跨海通道等，也引起广泛的关注。与陆地桥梁相比，跨海桥梁所处的自然环境更加复杂和恶劣，如波浪、海流(后文简称波、流)等时变荷载的持续作用，在我国东南沿海等高烈度地震区还面临地震的严重威胁。因此，此类桥梁在波、流环境中的响应特性及其抗震设计是需要研究的重要课题。

近几十年来，相关学者对于海洋结构物在地震和波浪联合作用下的动力响应问题先后开展了研究。Yamada等[2]引入Bretschneider波浪能量谱考虑水的影响，分别对地震和波浪作用下桩柱上的动水压力进行了对比分析。Jain[3]采用随机振动方法研究了海上结构物同时受波浪和地震作用的动力特性。Etemad等[4]对比分析了波浪与地震同向、不同向激励下海洋自升平台的非线性动力响应，结果表明，当二者同向作用时波浪会减小平台的地震响应，否则响应可能增加。Venkataramana等[5]讨论了近海结构在随机波浪和地震作用下的非线性动力响应特性。郑向远等[6]开展了近海风力发电机单桩基础在波浪和地震联合作用下的30∶1缩尺模型试验，表明如忽略波浪效应会低估结构的动力响应。

深水桥梁方面的相关研究主要集中于我国。李忠献等[7]对比分析了深水桥梁在地震、波浪单独或联合作用下的动力响应，发现二者共同作用下的动力响应并不是单独作用时的简单叠加，这一结论也得到文献[8]的验证。袁卫国等[9]以湛江东海岛大桥桥墩为对象开展了动力计算，结果表明，波浪和地震同时作用时，桥墩桩顶弯矩、桩顶水平力、桩底最大弯矩和配筋需求等比地震单独作用时有显著的增长。丁阳等[10]采用随机动力分析方法对比研究了深水桥墩在地震、波浪单独及共同作用下的响应特性。目前，围绕海洋工程结构物及跨海桥梁结构开展地震、波浪和海流共同作用的研究还非常少见。陈国兴等[11]分析了考虑与否波、流作用时群桩基础桥墩的地震响应特性，结果表明，顺流向桩体位移、弯矩增大，逆流向减小，其影响幅度随海流流速的增加而增大，且波、流作用效果与输入地震动特性密切相关。柳春光等[1]对跨海桥梁结构在波浪、海流、地震等荷载单独或联合作用下的研究进展进行了系统的综述与展望。吴安杰等[12]对某深水群桩基础桥墩体系的动力反应分析表明，波流与地震之间存在相互影响，波流对地震响应的影响范围为-31.6%～63.5%。

对既有研究的梳理可发现，国外研究主要以海洋平台、近海风力发电机基础等为对象，近年来我国学者逐渐开始了深水桥梁在地震、波流作用下动力响应特性的研究，但文献[11-12]均采用Morison方程近似考虑外部激励对结构产生的动水效应，难以全面模拟波流、地震与结构之间的双向耦合动力作用。因此，本文以跨海深水桥梁工程为背景，建立可考虑波浪、海流、地震共同作用的深水桥墩精细化双向流固耦合模型，采用全数值有限元法开展动力时程分析，提炼海流流速、波浪相位、周期、波高等波、流参数及水深对深水桥墩地震响应的影响规律。

1 波浪、海流的数值模拟

1.1 流体控制方程

在笛卡尔坐标系下，三维不可压缩黏性层流的运动规律可用Navier-stokes方程描述为

( 1 )

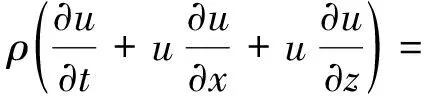
( 2 )

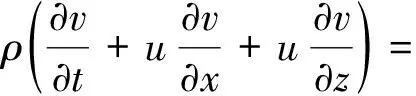
( 3)

式中：ρ为流体质量密度；u、v分别为流体沿x、z方向的速度；p为压力；μ为动力黏滞系数；t为时间；g为重力加速度；Sm为质量源；Sx、Sz分别为x、z方向的动量源。

1.2 波浪

1.2.1 波浪模型

本文采用Stokes 2阶波浪理论描述近海波浪，其主要控制参数为：周期T、波高H、水深d，水质点水平、竖向速度函数u、v及自由波面函数η表达式为

( 4 )

( 5 )

(2+cosh2kd)cos2(kxd-wt)

( 6 )

式中：k为波数；w为波浪圆频率；Δ为距静水位的距离，如果与重力加速度同向，则Δ为负；xd为距入射边界距离。

1.2.2 造波原理

主要的数值造波方法包括动边界造波法、设置造波边界法、设置造波区域法、动量源项造波法等，本文引入造波效果可靠的动边界造波法[13]，通过在数值波浪水槽入口处设置运动边界模拟推板造波机造波，可实现规则波浪(如线性波和Stokes非线性有限振幅波)的合理模拟[14]。造波板的运动速度为[13]

( 7 )

式中：η是给定的波浪过程(自由波面函数)，如η=Acoswt，其中,A为波幅；X是造波板位置，是时间t的函数；T(w)是造波板运动与给定波浪间的传递函数，其表达式为

( 8 )

1.2.3 数值波浪水槽模型

采用具有强大的多场耦合计算能力的ADINA软件实现波浪的数值模拟。海水体积模量E=1.0×1020Pa，密度ρ=1 025 kg/m3，动力黏滞系数μ=1.01×10-3kg/(m·s)，重力加速度g=9.81 m/s2。海水可假定为不可压缩黏性层流，采用8节点六面体3D-Fluid单元模拟，应用基于有限体积技术的FCBI-C单元算法进行方程离散，该算法适用于大规模问题的求解，具有稳定性强、精确度高的优点。采用分离法(SIMPLE)进行迭代求解。

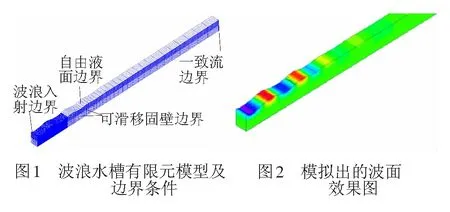
根据波、流场的实际，水槽底面和侧面用可滑移固壁模拟，上表面为自由液面，左边界(波浪入口)为造波板运动边界，右边界(波浪出口)采用一致流边界模拟无限远边界效果[15-16]。数值波浪水槽的有限元模型见图1。模拟出的波面效果见图2。

1.2.4 三维数值造波方法检验

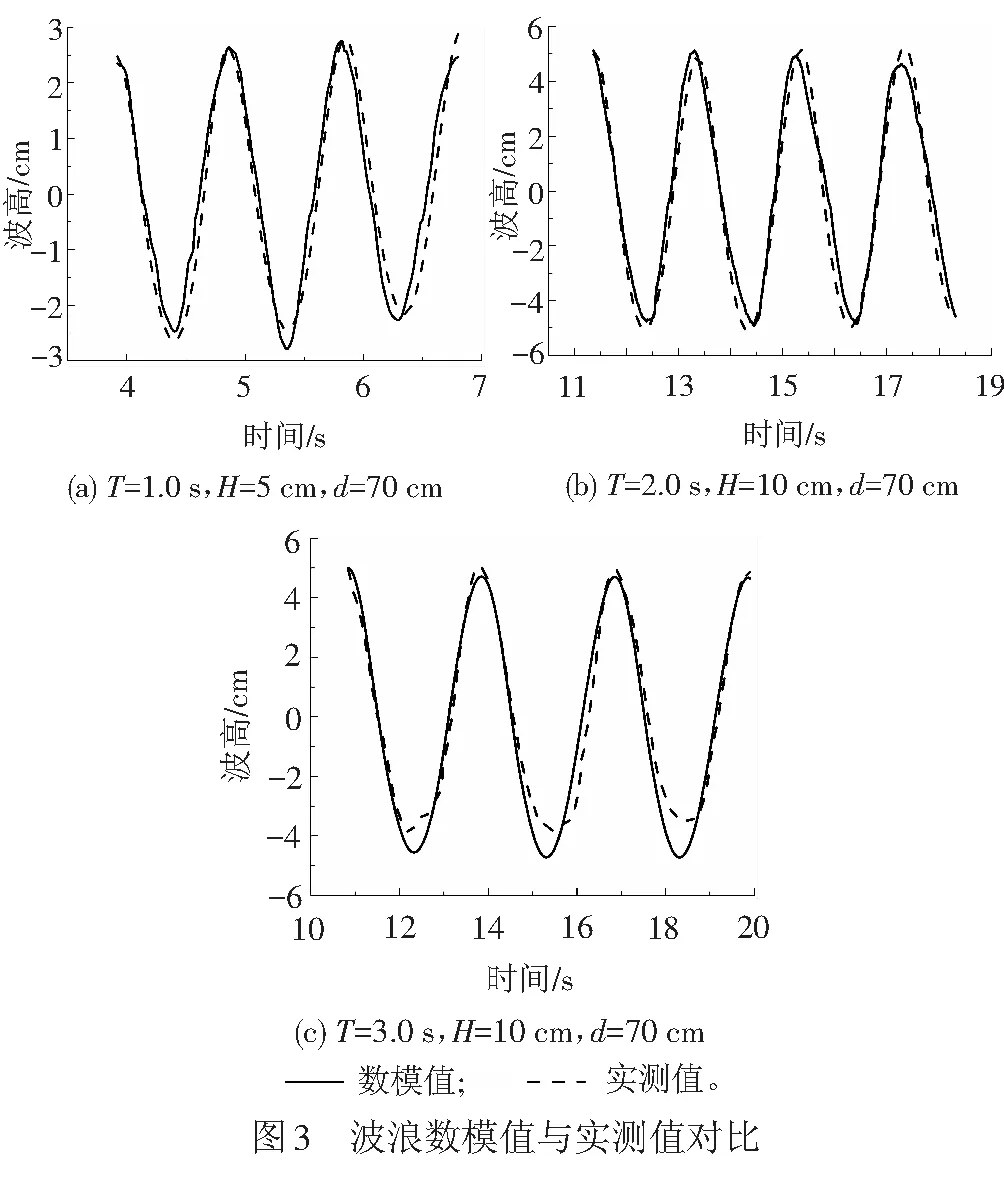
为了验证本文数值造波方法的合理性，采用大连理工大学海岸与近海工程国家重点实验室多功能综合水池实测波高数据[17]为基准，对不同波浪参数下Stokes 2阶波浪的波高时程模拟值进行了对比检验，见图3。可看出，采用数值方法模拟所得波浪的波高、周期均和实验数据吻合良好，波形稳定可靠。波高数模值与理论值[18]的对比见图4，由图4可见，波形稳定后的模拟波浪与理论值吻合很好。上述不同方法所得结果的对比表明，本文使用的动边界造波法可有效实现近海非线性波浪的模拟。

1.3 海流

在实际海洋环境中，特别是在近岸区，海流的影响不可忽略[19]。工程中，海流对柱体的作用力通常可仅考虑为拖拽力，且由于海流的速度随深度变化缓慢，一般认为同一垂线上的海流速度近似相等[20]，因此，在近海区可将其视为均匀定常流。限于问题的复杂性且相关资料不足，本文暂不考虑海床构造的影响，通过在数值波浪水槽入口处设置流体速度荷载uc=(1, 0, 0)实现海流的有效模拟[21]，海流方向与波浪传播方向一致，即沿x轴正向。根据统计，本文中海流流速范围取为1～4 m/s。

2 深水桥墩流固耦合计算模型

2.1 算例桥梁背景

选取两座跨海桥梁的圆形桥墩为例，第一座桥墩取自某跨海桥梁的引桥段，其计算跨度为51.1 m，上部结构为预应力钢筋混凝土梁，桥墩直径D=6 m，墩高h=30 m，记为D6-h30墩，C40混凝土，钢筋混凝土等效质量密度ρ1=2 500 kg/m3，弹性模量E1=3.0×104MPa，泊松比为0.2，桥墩所对应的梁体及桥面二期恒载的总质量为5 250 kg。第二座桥墩取自某跨海桥梁的2×64 m连续梁段，桥墩直径D=8 m，墩高h=63 m，记为D8-h63墩，C50混凝土，钢筋混凝土等效质量密度ρ2=2 760 kg/m3，弹性模量E2=3.45×104MPa，泊松比为0.2，墩顶上部结构质量为10 700 kg。对于两座算例桥墩，上部结构的质量以集中质量形式施加于墩顶。

为了对比分析不同波、流参数下深水桥墩的动力响应特性，需建立可精确模拟波、流、地震共同作用的深水桥墩多场流固耦合数值计算模型。

2.2 流固耦合数值模型

2.2.1 流场合理水域范围及网格划分

本文作者研究发现[22]，沿波浪传播方向，流场长度达到4L(L为波长)时，即与近海波浪参数相对应的水域长度范围为200～412 m时，波浪波动趋于稳定；在流场宽度方向，当水域宽度≥14D时，可有效避免墩柱存在引起水槽两侧固壁出现反射波浪，动力响应趋于稳定。此外，为减小波浪衰减和准确反映波浪在自由液面附近的模拟效果，对一定区域内的网格予以加密。流场网格划分见图5。

2.2.2 波、流场流固耦合数值模型

分别在ADINA软件的结构模块和流体模块中建立桥墩模型(图6(a))和波、流场模型(图6(b))，并将上述两个模型进行流固耦合实现动力求解。图6(a)中，桥墩选用各向同性弹性材料模型，采用三维实体单元(3D-Solid)模拟，墩顶集中质量采用质量单元(Mass)模拟，墩底固结，并在桥墩侧向壁面上设置可与波、流实现动力耦合计算的流固耦合界面(FSI)。图6(b)中，波、流场选用不可压缩粘性层流模型，底面和侧面为可滑移固壁(Slip Wall)，上表面为自由液面(Free Surface)，左边界(波浪、海流入口)为造波板运动边界，右边界(波浪、海流出口)采用一致流边界(Uniform Flow)模拟无限远边界效果，流体与桥墩间接触面设置为流固耦合界面(FSI)。

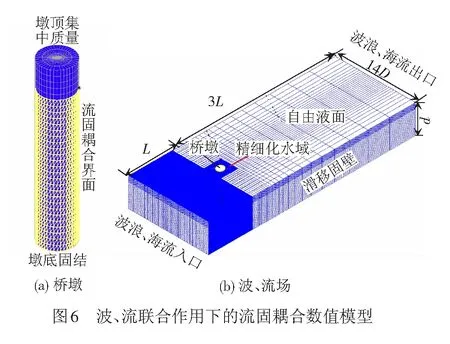
当同时考虑地震的作用时，深水桥梁基础将处于一个由绕射波浪、海流以及地震激励产生的辐射波浪共同组成的综合性波、流场，其动力平衡方程可表示为

( 9 )

3 不同荷载环境下深水桥墩的动力响应特性

深水桥墩所处的近海海域波、流条件复杂，波浪、海流及地震的共同作用，是典型的多场耦合动力问题。为了检验模型的合理性并讨论不同荷载环境下的动力响应特征，以D8-h63墩为对象，选取波、流参数为T=8.0 s，H=6 m，d=50 m，φ=3π/2，uc=1～ 4 m/s。

对于所用地震记录，依据文献[23]中给出的选波原则选取。限于多场耦合模型动力计算的效率，本文选取了2条代表性的近、远场记录开展动力计算：1979年Imperial Valley-06地震El Centro-Meloland Geot Array台站水平记录，近场H-EMO000波；1984年Morgan Hill地震San Justo Dam台站水平记录，远场SJL270波。根据桥址所在场地的抗震设防水平，将其峰值加速度均调整为0.2g，地震波输入方向与波、流传播方向一致。

3.1 波、流联合作用

波、流联合作用下不同时刻的流体竖向位移云图见图7。

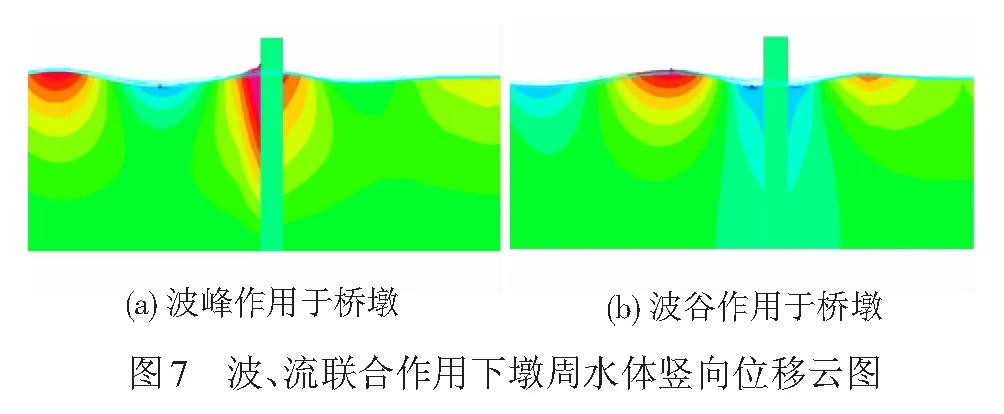
图8为波、流联合作用下桥墩的加速度分布特征(图8(a))及桥墩不同高度h1处截面的加速度响应时程(图8(b))。由图8可知，桥墩加速度随墩柱高度增加而增大；在波浪达到桥墩之前，桥墩先后经历了水流的瞬间冲击和随后的衰减阶段，由于水流的脉动性以及墩后漩涡释放，桥墩响应具有明显的波动性；当波浪到达桥墩后，波浪与稳定绕流共存，且波浪作用占主导；瞬态冲击阶段的响应大于稳态绕流阶段，这一现象与文献[24]结果一致。

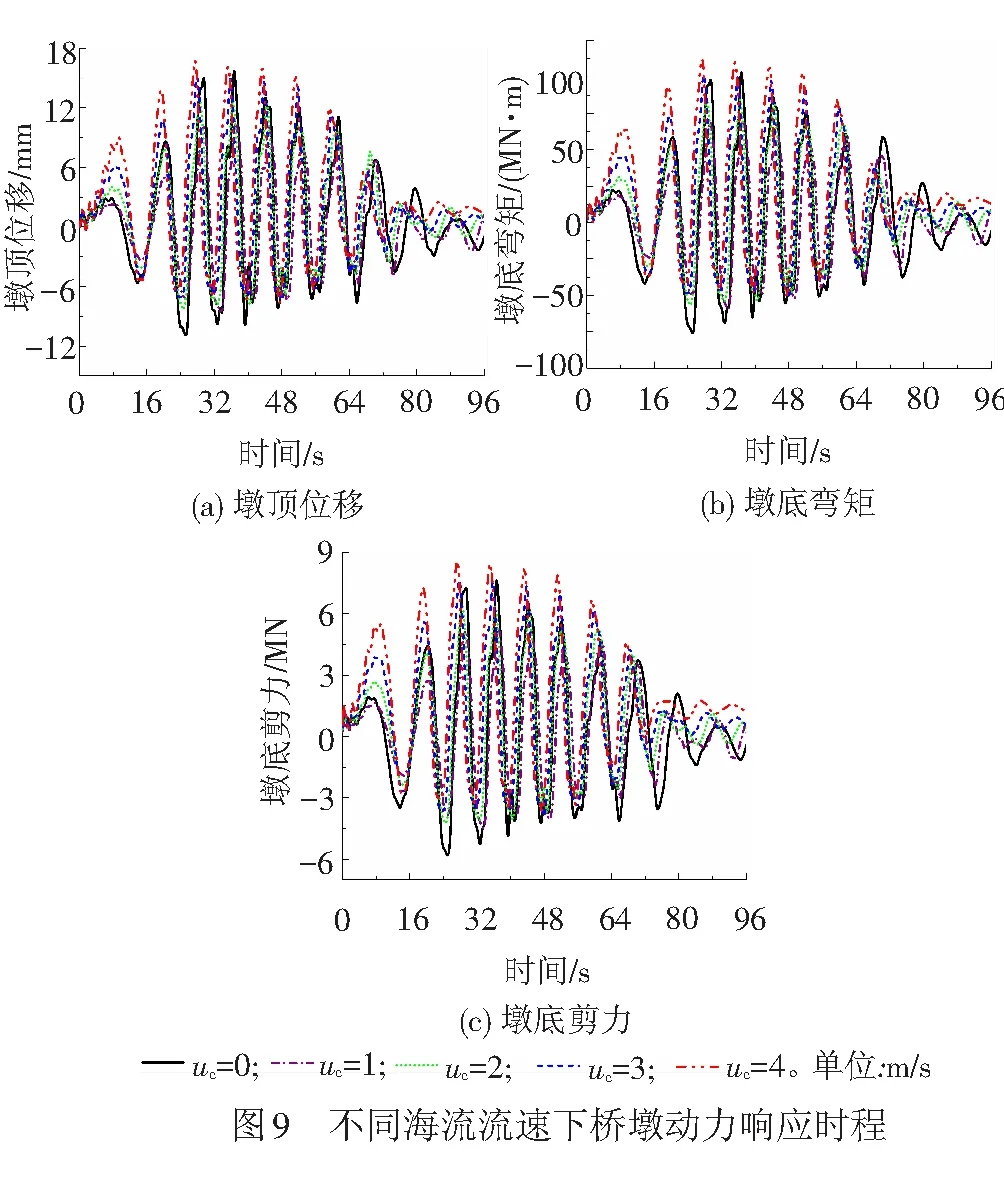
图9为不同海流流速下波、流联合作用时的桥墩动力响应时程，其中uc=0代表波浪单独作用，其他工况代表波浪与不同流速的海流共同作用。由图9可发现：(1)结构动力响应稳定后，不同流速下桥墩的响应值随时间呈近似正弦分布，其振动周期为8.0 s，与输入波浪的周期相吻合，即在稳定流条件下波浪周期不会因波浪、水流的相互作用而改变[25]。(2)由于所输入的波浪为Stokes 2阶非线性波，且波、流共同作用具有强非线性，桥墩的响应在零轴两侧呈不对称分布。(3)由于波、流同向，海流对波浪具有推动作用，使波浪传播速度加快，因此，随着海流流速的增大，桥墩达到响应峰值的时间相应提前，这一现象与文献[26]以海上浮式弹性板为对象的数值模拟结果相一致。(4)波、流联合作用时，波浪的作用占主导。

3.2 波、流及地震共同作用

深水桥墩在波浪、海流及地震下的共同作用见图10，墩周水体的水平位移云图见图11。由图11可看出，波、流环境中，地震激励下墩周水体会产生以桥墩为中心向四周扩散并逐渐衰减的水平位移。这是因为，入射波、流尤其是地震波的激励使得桥墩产生水平向往复运动，在墩周产生辐射波浪进而对墩周波、流场产生影响，较好揭示了波、流环境中深水桥墩受地震激励时的双向流固耦合过程。

限于篇幅，图12、图13以SJL270地震波输入为例，对比讨论了地震单独作用、波和流联合作用以及波、流与地震共同作用下墩顶加速度、位移及墩底弯矩、剪力时程的对比。为使地震动激励时桥墩已处于充分发展的波、流场中，同时为了加强对比度，响应时程的前24 s仅考虑波、流作用，见图12(b)。由图12(a)可知，虽然波、流联合作用下墩顶加速度较波、流与地震共同作用小很多，但仍然会对桥墩不同时刻的加速度响应产生影响。

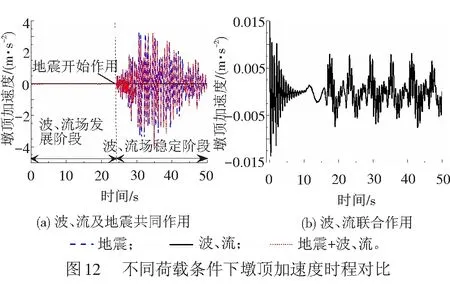
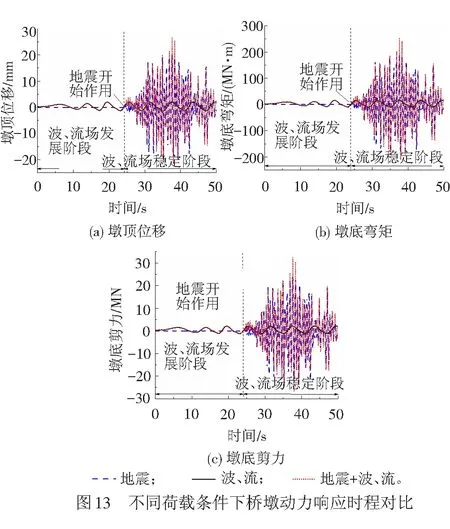
由图13可知，波、流联合作用下墩顶位移、墩底弯矩和剪力比地震单独作用以及波、流与地震共同作用时较小；波、流与地震共同作用时，地震的作用占主导，其响应特征与地震单独作用时相同；由于波、流的存在，不同时刻的响应值与地震单独作用下存在一定差异，说明波、流环境会对桥墩的地震响应产生影响。桥墩在波、流与地震共同作用下的峰值响应最大，墩底截面的最大拉应变为0.000 23，超过了混凝土的极限拉应变0.000 1，但在图13(b)和13(c)中，墩底弯矩、剪力峰值分别为254.0 MN·m、32.2 MN，并未超过本算例桥墩的屈服弯矩387.0 MN·m和抗剪承载能力120.4 MN，表明算例桥墩仍基本处于弹性工作状态。

4 波、流参数影响规律分析

由于波浪和海流的随机性，有必要分析波、流参数(如海流流速uc、波浪相位φ、波浪周期T、波高H及水深d等)对水中桥墩动力响应的影响规律。考虑计算效率，以D6-h30墩(矮墩)为对象，讨论波浪周期、相位及水深的影响规律；同时，为了较好地覆盖近海常见波高范围1～6 m和更强的海流作用，在讨论波高和海流流速的影响规律时，以D8-h63墩(高墩)为对象开展分析。

4.1 海流流速

讨论海流流速的影响时，设定算例桥墩所处波浪、海流环境的参数为T=8.0 s，H=6 m，d=50 m，φ=3π/2，拟讨论的海流流速范围为uc=1、2、3、4 m/s。

不同海流流速下桥墩在各荷载环境的动力响应峰值见表1。由表1可知，波、流联合作用时桥墩响应峰值随海流流速uc的增加而增大，但均明显小于地震单独作用下的响应峰值。波、流及地震共同作用下桥墩的动力响应峰值随流速的增加先增大后减小，对于本算例，在流速uc=2 m/s时取得最大值。其原因在于，海流对同向波浪具有推动作用[25]，而不同流速会改变波浪力峰值与地震波加速度峰值之间的相位差，在uc=2 m/s时，波、流与地震动响应的叠加效应最大，因此此时桥墩的动力响应峰值达到最大。对比还可发现，波、流及地震共同作用下桥墩响应峰值不是地震单独作用以及波、流联合作用这两种工况下的简单叠加，既可能大于也可能小于前者，其原因是地震和波浪间存在相位差，导致与两类荷载相对应的桥墩动力响应峰值并不在同一时刻出现[8,11]。

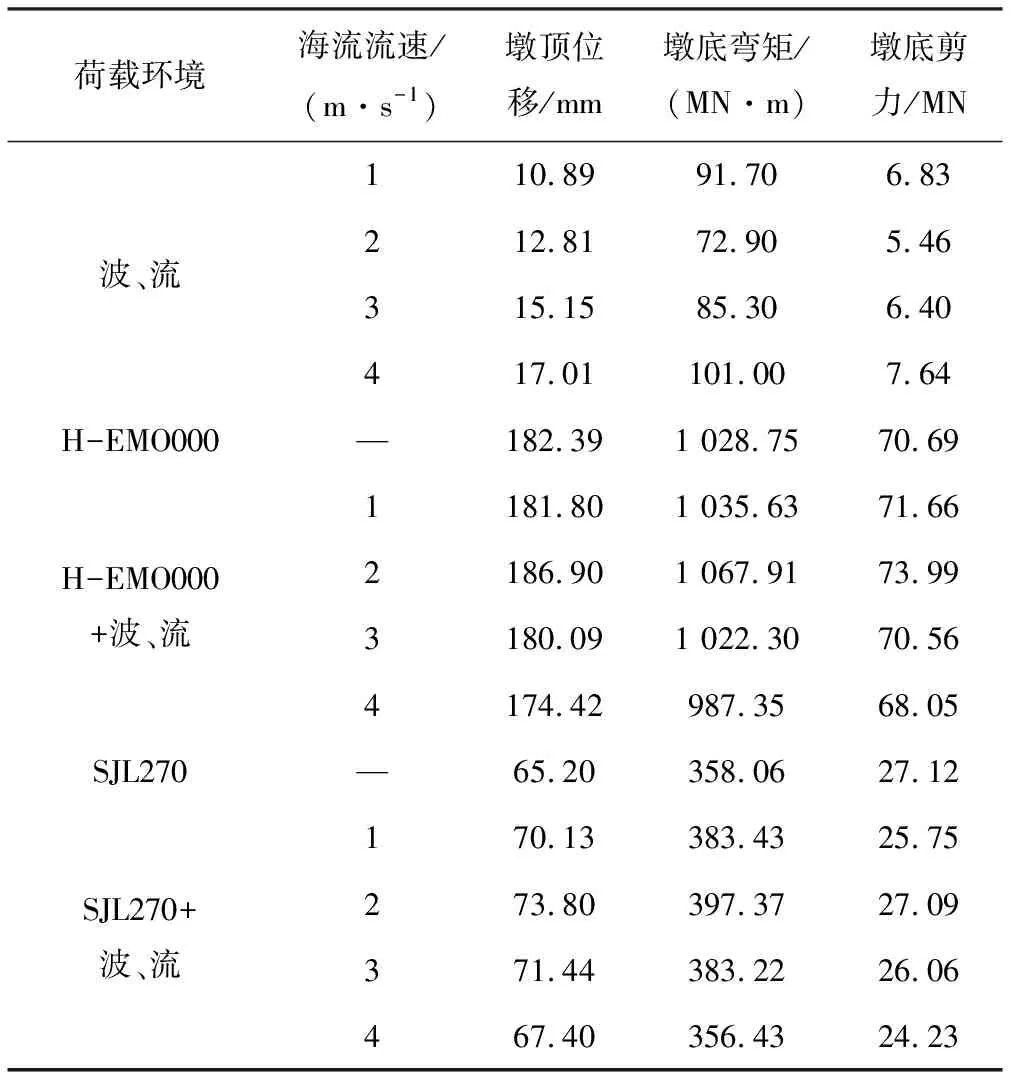
表1 不同海流流速下深水桥墩动力响应峰值

为了更好地量化评价波、流参数对桥墩动力响应的影响程度，参照文献[11]，定义波、流影响系数为

(10)

(11)

(12)

式中：Kpd、KM、KQ分别为波、流环境对桥墩墩顶位移、墩底弯矩以及剪力等动力响应指标的影响系数，Kpd、KM、KQ为正值时表示波、流环境增大桥墩的地震响应，为负值时则相反；Rl-pd、Rl-M、Rl-Q分别为波、流及地震共同激励时桥墩墩顶位移、墩底弯矩和剪力峰值；Re-pd、Re-M、Re-Q分别为地震单独作用时桥墩墩顶位移、墩底弯矩和剪力峰值。

不同海流流速下Kpd、KM、KQ的分布见图14。由图14中可看出，随着流速的增加，波、流影响系数均先增大后减小。两条地震波下，存在较为明显的差异，当流速uc=2 m/s时，SJL270波下Kpd、KM、KQ分别为13.19%、10.98%、-0.11%；而H-EMO000波下分别为2.47%、3.81%、4.67%。此外，从图14中还可发现，波、流影响系数也可能为负值，即波、流环境既可能增强也可能减弱桥墩的地震响应。例如，在SJL270波作用下，当uc=2 m/s时波、流对桥墩墩顶位移和墩底弯矩的增强作用最大，而当uc=4 m/s时，Kpd、KM、KQ分别为3.37%、-0.46%、-10.66%，波、流对深水桥墩墩底剪力的减弱作用达到最大。

4.2 波浪相位

讨论波浪相位的影响时，所对应的波、流参数为T=6.0 s，H=3 m，d=20 m，uc=3 m/s，拟讨论的波浪相位范围为φ=0、π/4、π/2、3π/4、π、5π/4、3π/2、7π/4。

不同波浪相位下桥墩在各荷载环境的动力响应峰值见表2。由表中可知，波、流联合作用时桥墩的动力响应峰值并不随波浪相位的变化而改变；波、流及地震共同作用下深水桥墩的动力响应随波浪相位的改变而呈不规则变化特征，但变化幅度较小。具体地，H-EMO000波作用下，当φ=π/4时，桥墩墩顶位移、墩底弯矩及剪力取得最大峰值，分别为70.67 mm、517.11 MN·m和66.17 MN；在SJL270波作用下，φ=3π/2时桥墩响应峰值达到最大，分别为29.56 mm、216.65 MN·m和27.67 MN。这是因为，波浪和地震波在本质上均为随时间变化的非平稳随机荷载，当波浪相位变化时，会使波浪力峰值和地震动加速度峰值之间的相位差也发生变化，从而导致桥墩总体动力响应有所改变。

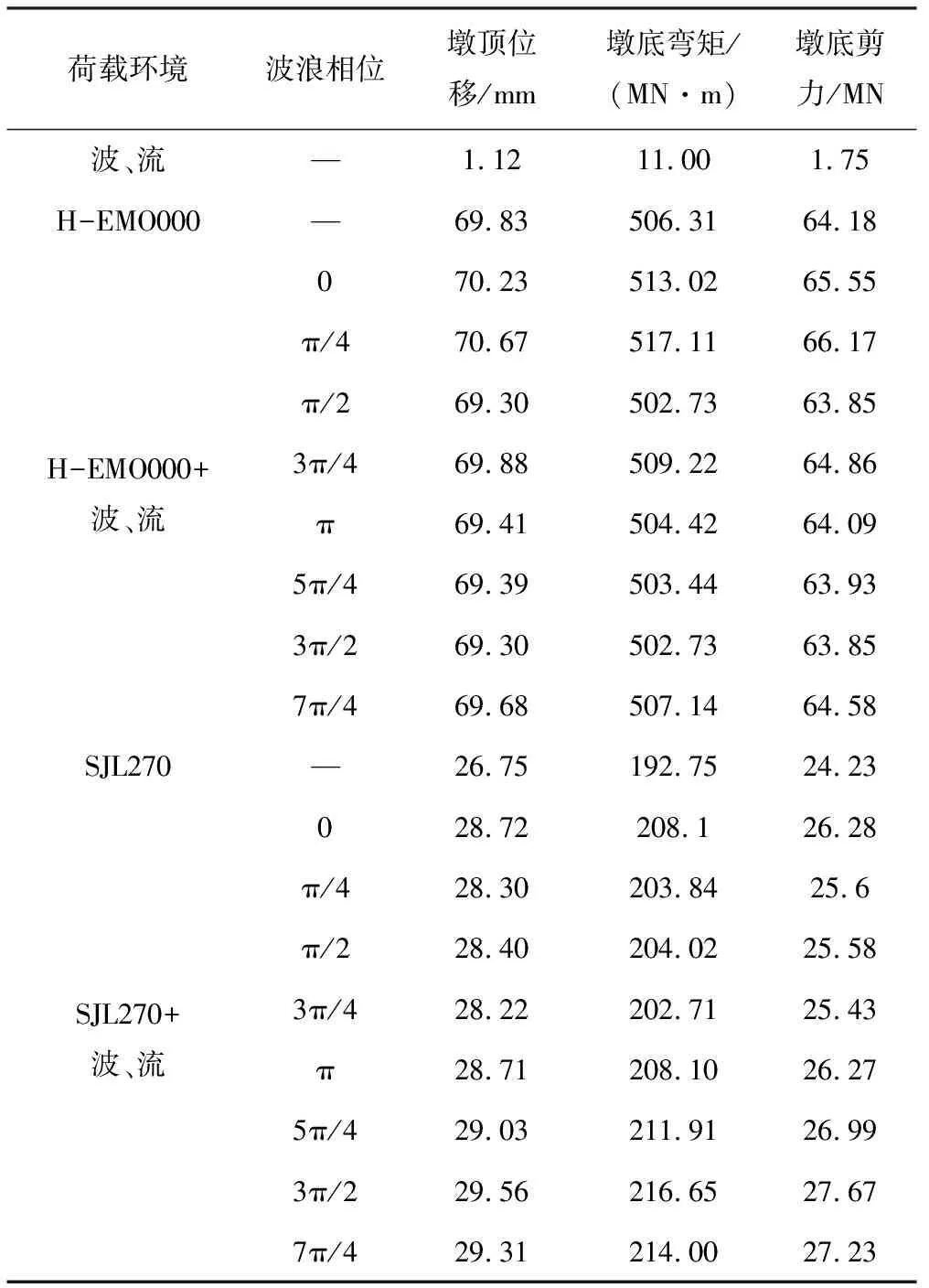
表2 不同波浪相位下深水桥墩动力响应峰值

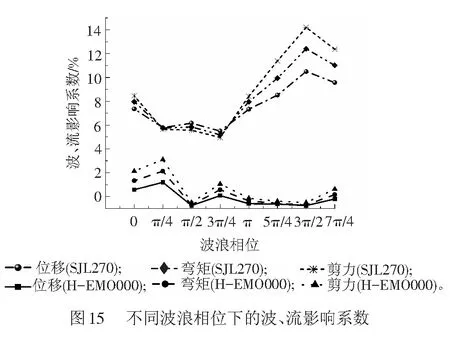
不同波浪相位下波、流影响系数的分布见图15，由图15可见，波、流影响系数随波浪相位增加而变化，不同相位下呈波动状态。并且，由于地震动频谱特性的不同，两条地震波下Kpd、KM、KQ在分布形态和量值上均有明显差异。例如，波浪相位由φ=0增加到φ=7π/4时，H-EMO000波下Kpd、KM、KQ的变化范围分别为-0.76%～1.20%、-0.71%～2.13%、-0.51%～3.10%；而SJL270波下则分别为5.50%～10.50%、5.17%～12.40%、4.95%～14.20%。此外，从图15中还可发现，在H-EMO000波作用下，波、流影响系数出现负值，说明相位差的存在使得波、流环境也可能减弱桥墩的总体动力响应。

4.3 波浪周期

讨论波浪周期影响时，所对应的波、流参数为H=3 m，d=20 m，φ=3π/2，uc=3 m/s，拟讨论的波浪周期范围为T为6.0、6.5、7.0、7.5、8.0、8.5、9.0 s。

不同波浪周期下桥墩在各荷载环境的动力响应峰值见表3。

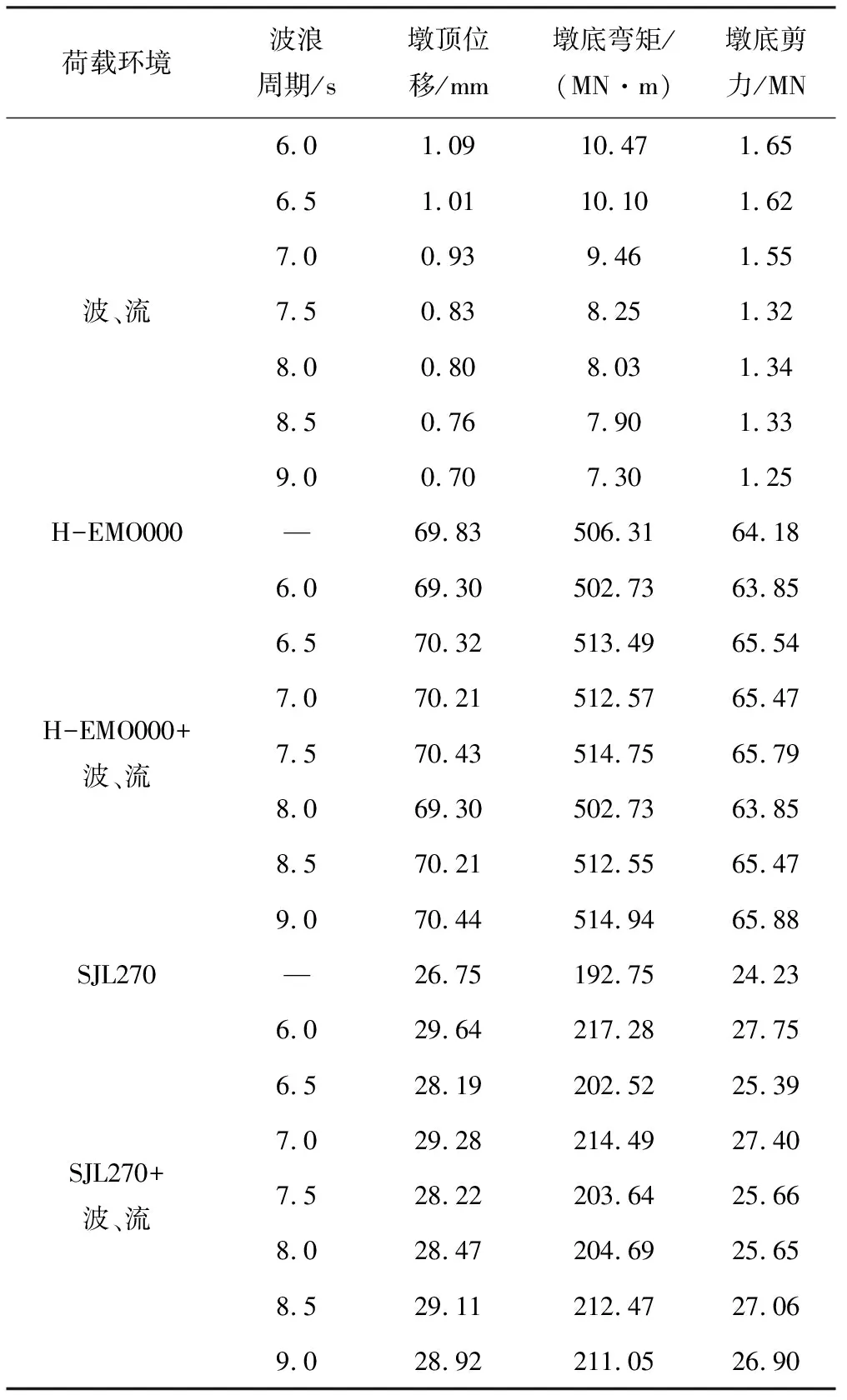
表3 不同波浪周期下深水桥墩动力响应峰值

由表3可知，波、流联合作用时桥墩响应峰值随波浪周期的增大而单调减小。这是因为，随着波浪周期的增加，其与算例桥墩第一阶自振周期T1= 0.64 s的差别越大，从而在其他参数不变的条件下导致桥墩动力响应变小。从表3中还可看出，不同周期下，波、流及地震共同作用时的桥墩动力响应峰值呈现出一定幅度的波动状态，波浪激励周期与结构自振周期之间的差异，以及波浪与地震动之间的相位差，是产生这种现象的主要原因。

不同波浪周期下波、流影响系数的分布见图16。由图16可见，两条地震记录下波、流影响系数均随波浪周期增大而波动。具体地，当波浪周期由6.0 s增加至9.0 s时，H-EMO000波下Kpd、KM、KQ的变化范围分别为-0.76%～0.86%、-0.71%～1.70%、-0.51%～2.65%；SJL270波下则分别为5.50%～10.80%、5.65%～12.73%、5.90%～14.53%。和前两种波浪参数下的结果相类似，H-EMO000波下的波、流影响系数也出现负值，说明一定的波浪周期下波、流作用可能降低桥墩的总体动力响应。

4.4 波高

为了讨论波高的影响，相应选取的波、流参数为T=8.0 s，d=50 m，φ=3π/2，uc=3 m/s，拟讨论的波高范围为H=1,2,…,6 m。

不同波高下桥墩在各荷载环境的动力响应峰值见表4。由表4可知，波、流联合作用时，桥墩动力响应峰值随波高的增加而显著增大，呈现出明显的规律性。从表中还可看出，波、流与地震共同作用时，H-EMO000地震动作用下桥墩的动力响应峰值随波高的增加而略有减小，而在SJL270地震动作用下桥墩响应随波高的增加而增大。

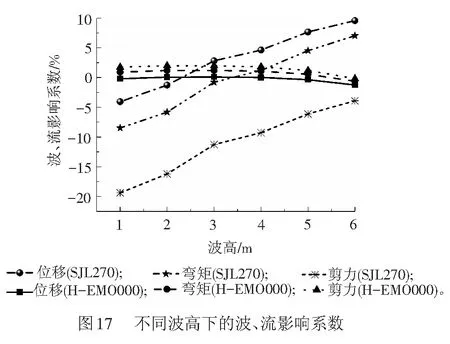
上述分布特征与图17所给出的波、流影响系数的分布相一致。由图17可看出，随着波高的增加，SJL270波作用下Kpd、KM、KQ均呈线性递增趋势，Kpd、KM、KQ的变化范围分别为-4.06%～9.57%、-8.50%～7.03%、-19.40%～-3.91%。在H-EMO000波作用下，Kpd、KM、KQ的变化均不明显，其变化范围分别为-1.26%～0.09%、-0.63%～1.19%、-1.99%～-0.18%。上述对比再次表明，波、流作用可能增强也可能减弱桥墩的地震响应，随波高的增加而发生变化，且不同地震动激励下，增强或减弱的程度存在差异。

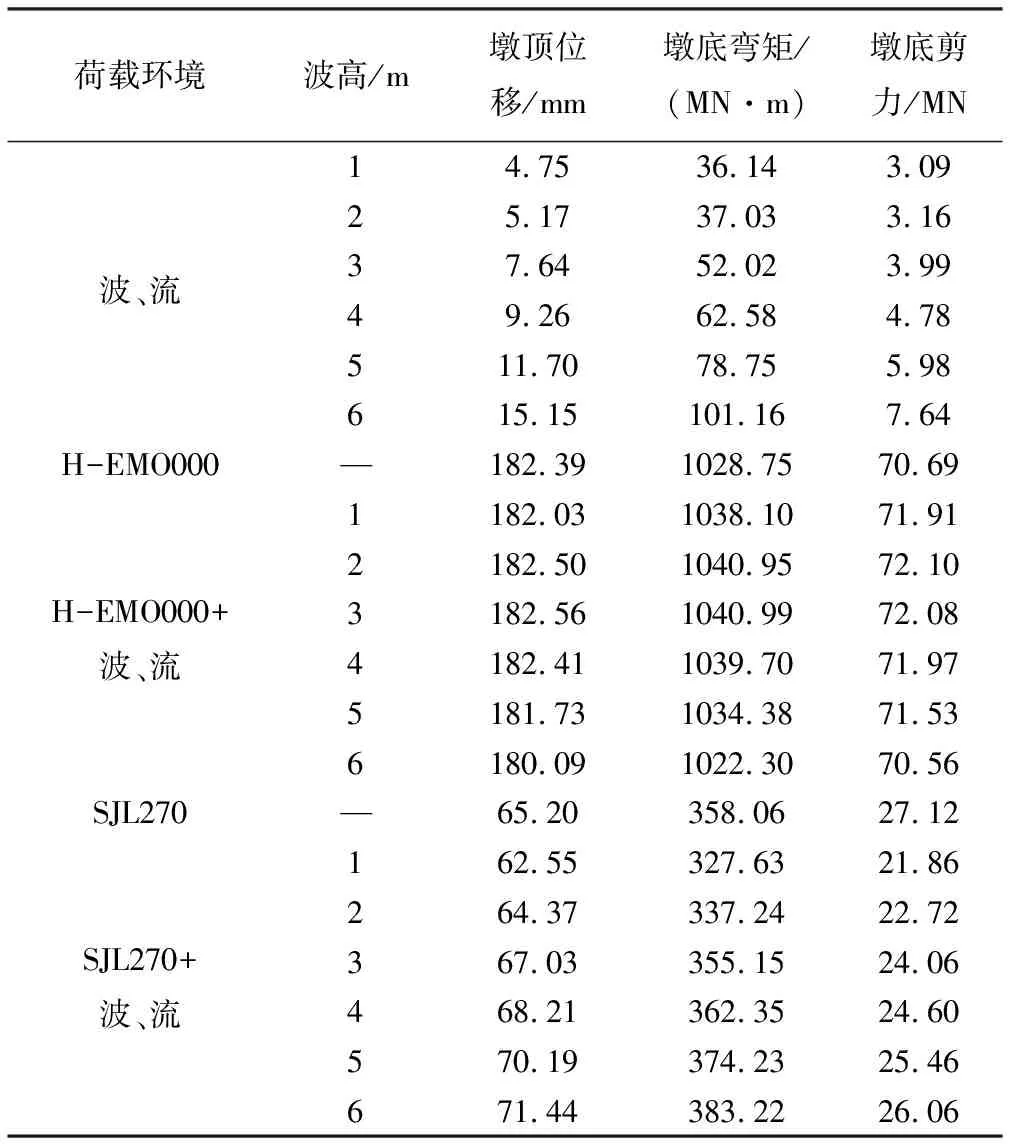
表4 不同波高下深水桥墩动力响应峰值

4.5 水深

讨论水深的影响时，对应选取的波、流参数为T=6.0 s，H=3 m，φ=3π/2，uc=3 m/s，拟讨论的水深范围为d=15、20、25、30 m。

不同水深下桥墩在各荷载环境的动力响应峰值见表5。由表5可以看出，波、流联合作用时，桥墩的响应峰值随水深的增加而总体呈稳步增大趋势，规律明显。波、流及地震共同作用下，两条地震记录下的响应结果呈现出不同的分布趋势。H-EMO000波下，桥墩动力响应峰值随水深增加而有所减小；SJL270波作用下，桥墩响应峰值随水深增加而有所增大，这种现象依然可归结为不同地震波在频谱特性上的差异以及其与波浪间相位差的区别。

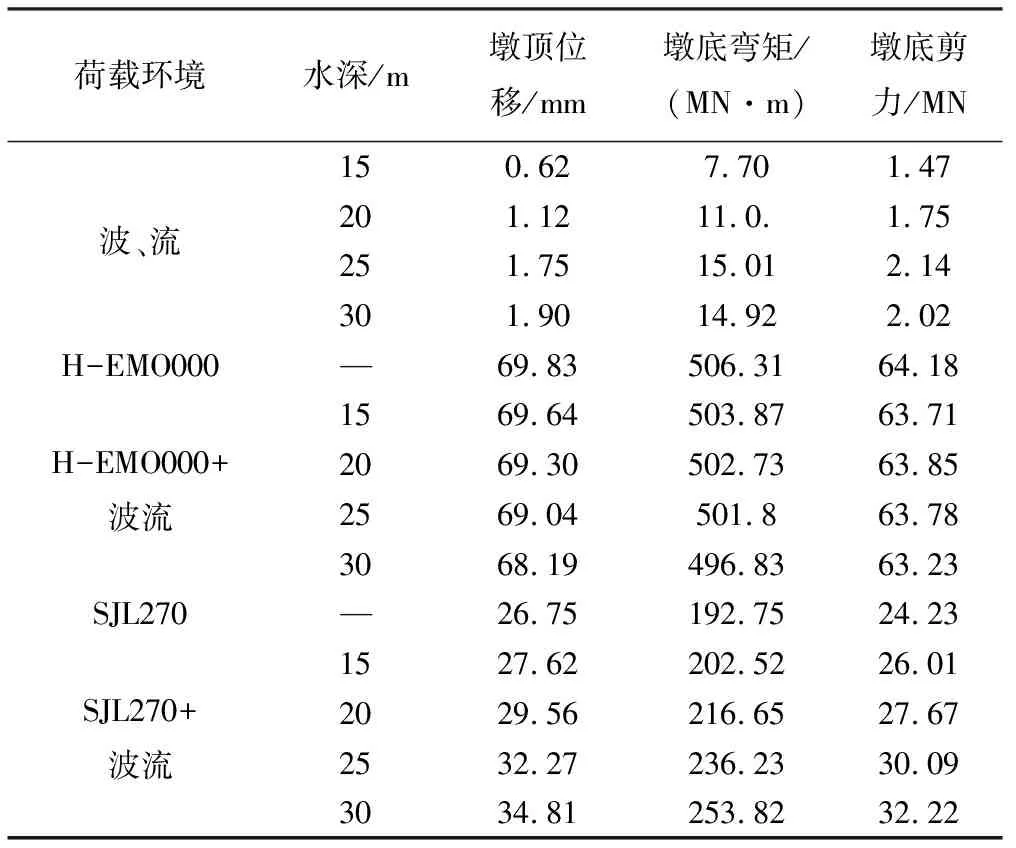
表5 不同水深时的深水桥墩动力响应峰值

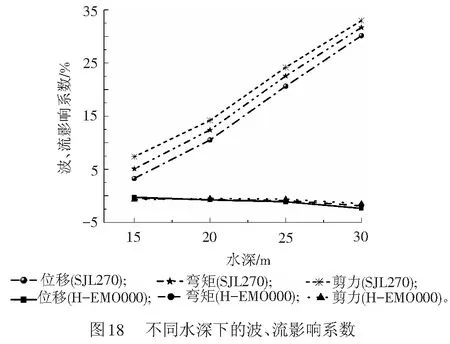
不同水深下波、流影响系数的分布见图18。从图18中可看出，两条地震波下的分布曲线存在明显差别。SJL270波作用下，Kpd、KM、KQ均为正值，且均随水深的增加而增大，在水深d=30 m时，Kpd、KM、KQ分别为30.13%、31.68%、32.98%，此时，波、流环境对桥墩地震响应的增强作用最为明显；而在H-EMO000波作用下，Kpd、KM、KQ均为负值，且均随水深的增加而减小，在水深为d=30 m，Kpd、KM、KQ分别为-2.35%、-1.87%、-1.48%，波、流环境对桥墩地震响应的减弱作用最大。上述现象出现的原因，与波浪相位、周期等指标的影响机理类似，和不同地震动在频谱特性上的差异有重要关系。

由上述不同波、流参数下的多荷载环境对比分析可知，波浪、海流与地震对桥墩共同作用的相互作用机理十分复杂，不同地震动输入、不同波、流要素下桥墩的总体响应存在显著的差异。其原因可能包括以下三个方面：(1)波浪和地震动均为非平稳随机过程，二者的频谱特性存在显著差别；(2)波、流与地震共同作用时，波浪和地震波之间势必存在相位差，不同波、流参数下相位差的变化会对结构总体动力响应产生不同方向和程度的影响；(3)波、流和地震荷载的作用位置不同，波浪主要作用在近水面的墩身上，海流作用于全水深的墩身上，而地震荷载则作用于桥墩底部，范围和幅度存在差别。