管内旋流特性与传热效果的关联性分析

王宗勇， 陈科昊， 信东明

(沈阳化工大学 能源与动力工程学院， 辽宁 沈阳 110142)

利用扭旋元件提高换热管内流体的换热效果是一种典型的传热强化方式.扭旋元件的结构形式和排列方式决定了管内旋流特性，进而影响到换热管的对流传热效果.国内外研究学者针对多种形式扭旋元件的传热强化效果进行了深入研究[1-7]，研究结论对于内置扭旋元件换热器的工业化应用起到了较大的促进作用.纵观传热强化论文，会发现绝大多数文章侧重于元件结构对传热效果的影响，关于螺旋流特性与传热效果之间存在的必然联系缺乏深入的理解，特别是两者之间的定量关系研究更少.这种现状不利于螺旋流强化机理的深入理解以及新型扭旋元件的研制开发.

螺旋流的传热强化机理基本得到共识，其可归纳为以下三个方面：一是管壁传热边界层在螺旋流离心压力场的作用下厚度减薄，径向温度梯度增大；二是管内螺旋流可形成二次涡流，流体的径向流动方向与热量传递方向夹角更小，更加符合场协同理论；三是螺旋流的三维流动使主流核心区的速度和温度分布更为均匀，提高了传热边界层径向温差.由此可见管内流体的传热效果是由旋流特性决定的，而旋流特性主要表现为螺旋流的三维速度分布，其中周向速度和径向速度在传热强化过程中起到了决定性的作用，也是区别于光管换热的根本标志.在以往的传热强化研究过程中，对于流动特性更多的是侧重于速度场的定性分析，间接地表征其与传热效果的关系，缺乏直接定量的分析方式.若要分析螺旋流特性与传热效果之间的定量关系，必须利用特定的量去分别表征旋流特性和传热效果.传热效果通常采用传热系数即努赛尔数表征，而旋流特性用何种量来表征缺乏统一的认识.笔者认为，表征旋流特性的量必须体现旋流的三维流动特点，特别是要反映周向速度和径向速度的分布规律.在研究螺旋流旋流强度时，一般采用旋流数定量平均旋流的强弱，该物理量基本符合上述对于旋流特性表征的要求[8-16].旋流数更多体现的是周向速度对旋流特性的影响，由旋流传热强化机理可知径向速度也起到了至关重要的作用，为此，本文按照旋流数的构成方式提出了“径流数”概念，以该无量纲参数表征管内旋流的径向流动强弱，体现径向速度对螺旋流特性的影响.

本文的研究目的就是通过旋流数和径流数与努赛尔数建立起必然的定量联系，以此反映旋流特性和传热效果之间的关系.通过该关系可在不进行传热研究的前提下，初步确定扭旋元件的传热强化能力，指导扭旋元件的结构设计，缩短扭旋元件研制开发周期，也为内置扭旋元件换热管的工程应用提供技术支持.

1 旋流数和径流数

旋流数(S)最初用于研究旋流分离器的旋流强度，是一个无量纲参数，表示流体周向动量矩与轴向动量矩之比，其表达式可写为：

(1)

式中：uz为轴向速度；uθ为切向速度；r为流体质点径向坐标；θ为流体质点角度坐标；R为圆管半径.

参照旋流数的设定理念，提出“径流数”概念.径流数(T)同样是无量纲参数，表示流体径向动能与轴向动能之比，这样设定可有效避免径向速度方向变化对计算结果的影响，其表达式可写为：

(2)

式中：ur为径向速度；其余各符号含义与旋流数公式(1)中符号含义相同.

旋流数和径流数均表征了管内流体在某横截面上周向流动和径向流动的强弱，因此，对于未充分发展流而言，这两个参数均与轴向位置有关.同时，流体入口流动状态(雷诺数Re)和扭旋元件结构决定了管内流体的速度分布，旋流数和径流数也必然和这两种因素密切相关.努赛尔数(局部)同样受到轴向位置、雷诺数和元件结构的影响，因此，本文重点分析不同雷诺数和元件结构下，旋流数与努赛尔数、径流数与努赛尔数随轴向位置的变化关系，对比分析得到相互之间的关联性.

2 研究对象及模拟方案

2.1 扭旋元件

研究对象是由宽度和旋向不同的两块扭旋片(轴向长度及扭转角度相同)首尾垂直连接构成的扭旋元件，该扭旋元件同心内置安装在换热管内，其结构如图1所示.换热管内径D=20 mm,管长L=20D，扭旋元件前缘距入口间距L0=8D.两块扭旋片厚度均为δ=0.05D，宽度分别为W和D，长度均为H=2D，扭转角度均为θ=180°.

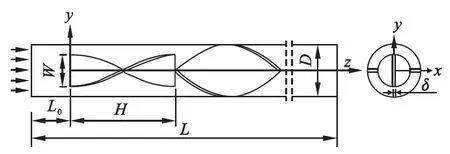
2.2 参数设定

定义宽度比e=W/D，通过改变较窄扭旋片宽度W，分析扭旋元件结构变化对流动特性和传热性能的影响.以管径作为雷诺数特征尺寸，即Re=ρu0D/μ，其中：ρ为流体密度；μ为流体动力黏度；u0为流体入口速度.本研究的雷诺数范围为Re=200～1800，主要研究在较低的雷诺数范围内旋流特性与传热效果之间的关系.

采用Solidworks软件建立扭旋元件几何模型，通过ICEM软件对流动区域划分结构化网格，利用Fluent 17.0对管内流动和传热过程进行数值模拟.采用常温(295 K)下的水作为工质，以均匀速度入口方式流进换热管，以压力出口方式流出换热管.换热管壁温恒定，设定为360 K.工质在扭旋元件及壁温作用下旋流流动并产生对流换热，沿着流动方向平均温度逐渐升高.

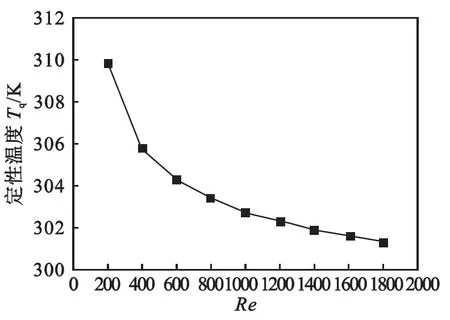
工程上，为了确定工质的物性通常采用进出口的算术平均温度作为定性温度.而实际上换热管长度范围内的体积平均温度更能真实反映流体物性状况，为此本文采用该温度作为定性温度.因为定性温度取决于管内流体的流动和传热状况，所以其必然与流动状态(雷诺数)相关.为获得每种流动参数下的定性温度，针对每种雷诺数下的流体流动进行多次模拟计算.首先，假定一个定性温度(高于入口温度)，确定该温度下的工质物性，进而进行数值模拟；然后，对模拟结果进行数据处理，得到换热管长度范围内的平均温度，若该温度与假定温度相对偏差小于1 %，则该假定温度即为定性温度，否则重新假定，直到上述条件满足为止.图2给出了不同雷诺数与定性温度的对应关系曲线，由图2可以看出：定性温度随雷诺数的增大而降低，而降低速度也存在相同的规律.这种现象说明：随着雷诺数的增大，管内流量提高，在热流密度变化较小的前提下(尽管对流传热系数有所增大)，工质平均温度变化量必然降低，这是由单位质量流量工质所得到的热量减少决定的.随着雷诺数的增大，最终的定性温度一定越来越接近工质入口温度.

在模拟过程中，对于离散控制方程，采用速度-压力求解器.整个流动区域所有物理量的迭代残差设定为10-6以下，同时检查Flux Reports对话框中流入和流出整个系统的质量、动量、能量不平衡误差，所有值均少于0.1 %，以保证求解收敛.同时假定：某一雷诺数下流体热物性保持恒定；流体为牛顿不可压缩稳态流体.

2.3 网格无关性检验

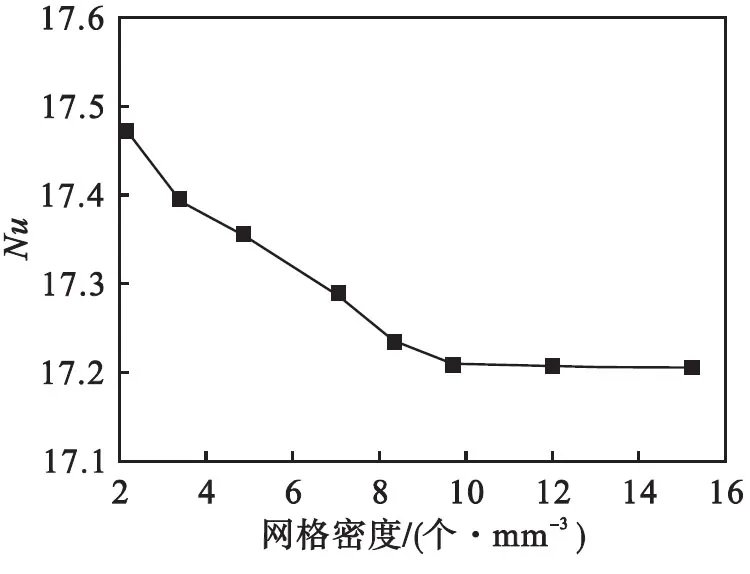
为消除网格尺寸对计算结果的影响，本文首先针对任意一种雷诺数及元件结构进行不同网格密度的网格划分，然后通过数据处理得到相应网格密度下的努赛尔数(Nu)，再根据不同网格密度下努塞尔数的变化趋势，确定与网格尺寸无关并具有良好计算效率的网格密度.以Re=600、e=1.0情况为例进行说明，在该情况下，本文对流动区域共计划分了8种网格密度网格，对应的努赛尔数与网格密度关系如图3所示.由图3可以看出：努赛尔数随着网格密度的增大，呈现逐渐下降并最终趋于恒定的变化趋势.本文选用网格密度为9.7个/mm3对应的网格尺寸对流动区域进行网格划分.

3 旋流特性与传热效果关系

3.1 旋流数与努赛尔数对比

为揭示管内旋流特性与传热效果之间的关系，绘制不同宽度比元件下，旋流数与努赛尔数、径流数与努赛尔数随轴向位置变化曲线，如图4所示.由图4可以看出：在扭旋元件前一个旋流片长度处到换热管出口长度范围内(旋流区域)，旋流数与努赛尔数随轴向位置变化趋势极其相似，各自的峰值轴向位置偏差不超过半个扭旋片长度；而在非旋流的入口区域(z/L=0～0.3),旋流数和努赛尔数变化规律明显不同，努赛尔数呈现下降趋势而旋流数保持恒定(零值).以上现象说明：在入口区域，流体呈现为未充分发展的管流，流体仅存在轴向速度，因此旋流数必定为零.但旋流数为零不代表传热不能进行，只不过随着流体由活塞流向泊肃叶流过渡，努赛尔数呈现下降趋势，这种变化规律说明轴向速度均匀分布同样能够强化传热，在以后的研究中有必要提出“轴流数”概念对轴向速度强化传热规律进行探究.

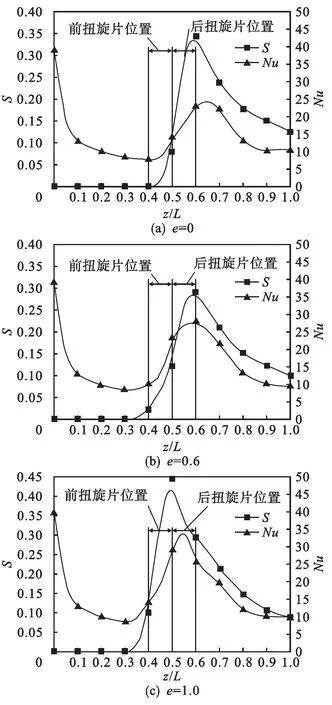
在旋流区域，流体在扭旋元件长度范围内，旋流强度和努赛尔数迅速提高并且同步良好，表明周向速度增大的确强化了对流传热.而在扭旋元件出口以后的长度范围内，流体失去了扭旋元件的旋流作用，流体旋流数明显下降，而努赛尔数也基本同步产生了下降.

通过以上两种区域旋流数与努赛尔数的对比分析可知：较高的旋流数意味着较高的努赛尔数，但零旋流数不代表较低的努赛尔数.努赛尔数实际上是管内三维速度综合作用的结果，为体现螺旋流自身的传热强化作用，将扭旋元件换热管与光管进行对比，将两者的努赛尔数差值作为旋流自身的强化作用.努赛尔数差值Nud=Nu-Nu0，Nu和Nu0分别为扭旋元件换热管和光管的对流传热系数.为了使旋流数与努赛尔数在数值上具有可比性，本文对这两个参数进行了相对处理，努赛尔数差值(Nud)与光管平均努赛尔数(Nu0m)对比，即Nud/Nu0m；扭旋元件换热管旋流数(S)与理想旋流数(S0)，即S/S0.光管平均努赛尔数Nu0m采用Sieder and Tate公式：

(3)

式中：Re，L和D各物理量含义与前节表述相同；Pr为定性温度下工质普朗特数；μ和μs分别为定性温度和壁温下工质动力黏度.理想旋流数S0利用螺旋流道形心位置处流体做理想螺旋运动时的速度分布确定.所谓理想螺旋运动是指流体做螺距等于扭旋元件长度的螺旋线运动，该螺旋线及速度分解关系如图5所示.

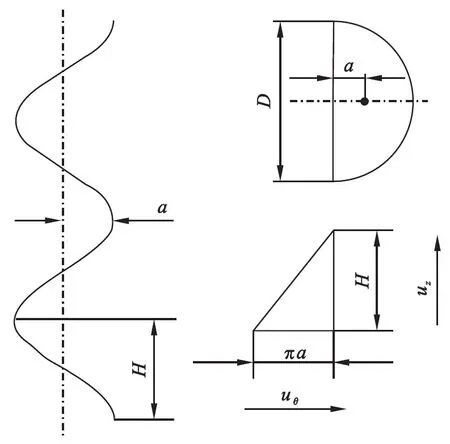
(4)

该式代表了扭旋元件对理想流体的旋流能力，没有涉及到流体物性及流动状态对旋流状态的影响.

相对值Nud/Nu0m代表螺旋流相对于直管流的传热系数提升幅度，S/S0代表螺旋流旋流数所占理想旋流数比例，这样处理不仅体现旋流自身的传热强化效果，也使这两个相对参数处于同一数量级内，更加便于相互之间比较分析.

图6绘制出了相对旋流数与相对努赛尔数对比曲线.

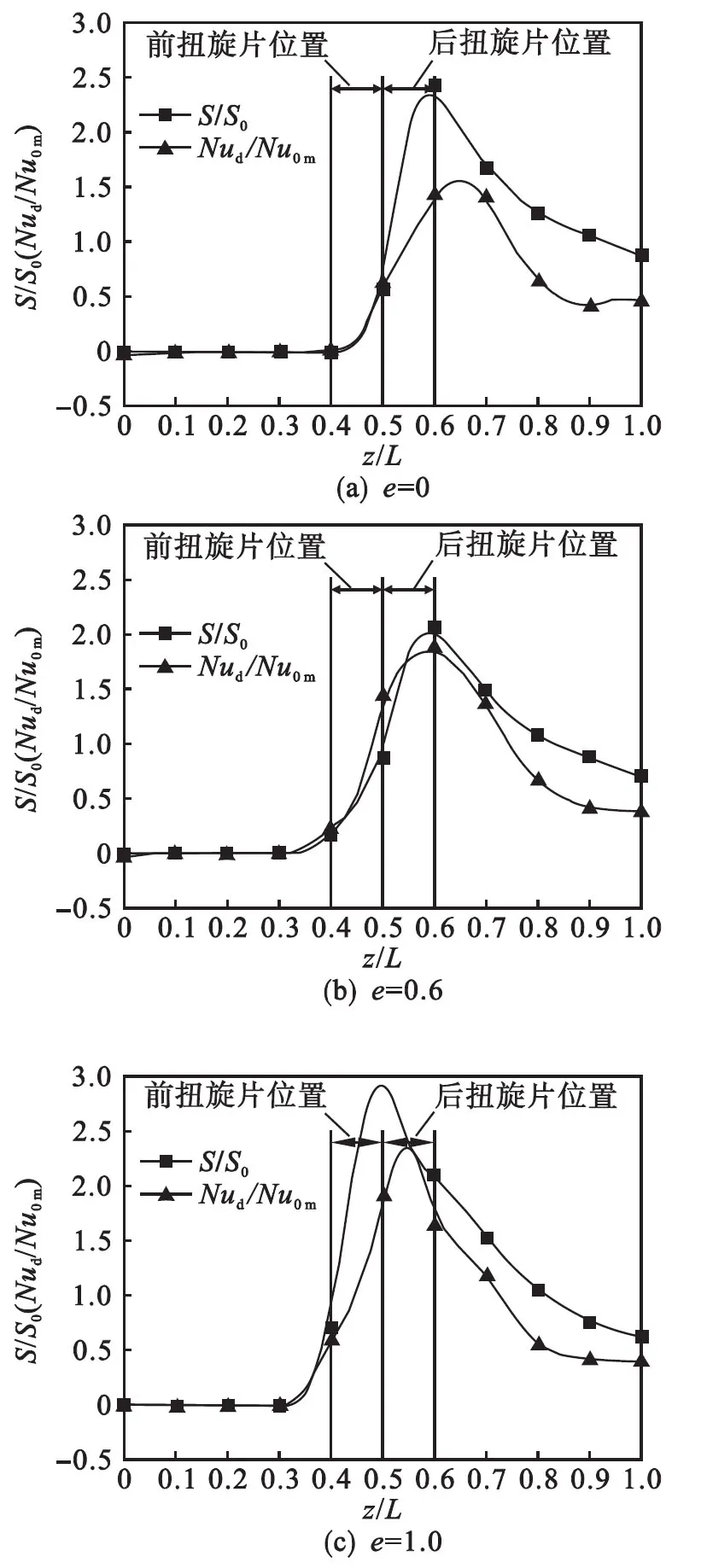
由图6可以看出：相对旋流数S/S0与相对努赛尔数Nud/Nu0m变化规律非常接近，各自极值位置也比较接近，两者位置偏差不超过半个扭旋片长度.在整个换热管长度范围内，利用相对旋流数表征相对努赛尔数完全可行，两者相对偏差不超过50 %.

3.2 径流数与努赛尔数对比

径流数是本文提出的一个全新参数，目的是通过该参数反映径向速度在旋流传热强化中所起到的作用.在流体旋流流动中，径向速度与其它两个方向速度相比是一个相对小量，往往要差一个数量级以上.但是流体质点走过的路径长度也是一个小量，可在较短的时间内往返于传热边界层和主流核心区.因此，径向速度在传热强化中所起到的作用不容小觑，大量的研究结果和工程应用均证明了这一点.

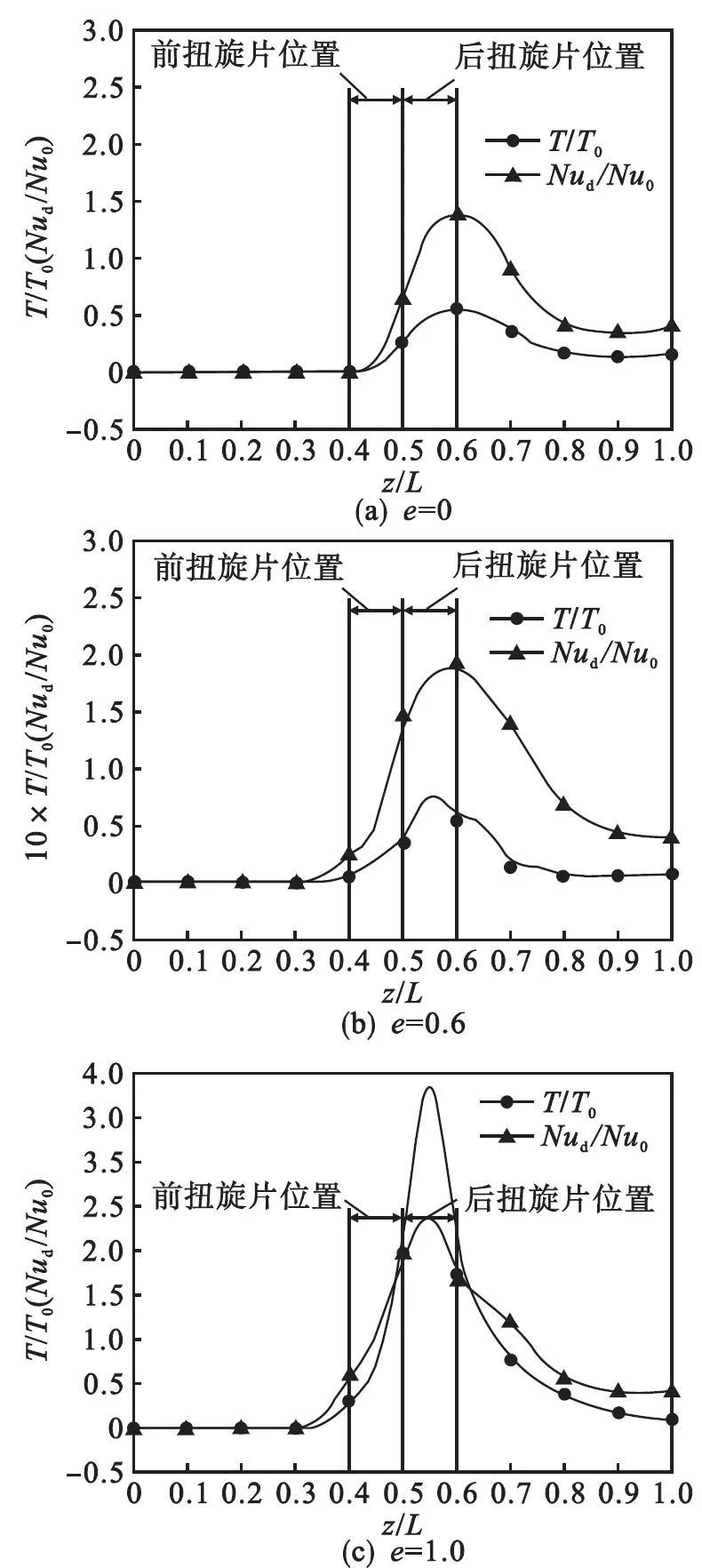
图7给出了径流数和努赛尔数随轴向位置的变化曲线.由图7可以看出：在扭旋元件以及其下游区域内，径流数与努赛尔数变化规律基本相同，出现对应极值的轴向位置甚至好于旋流数.因此，通过径流数同样能够表征螺旋流的传热强化能力.

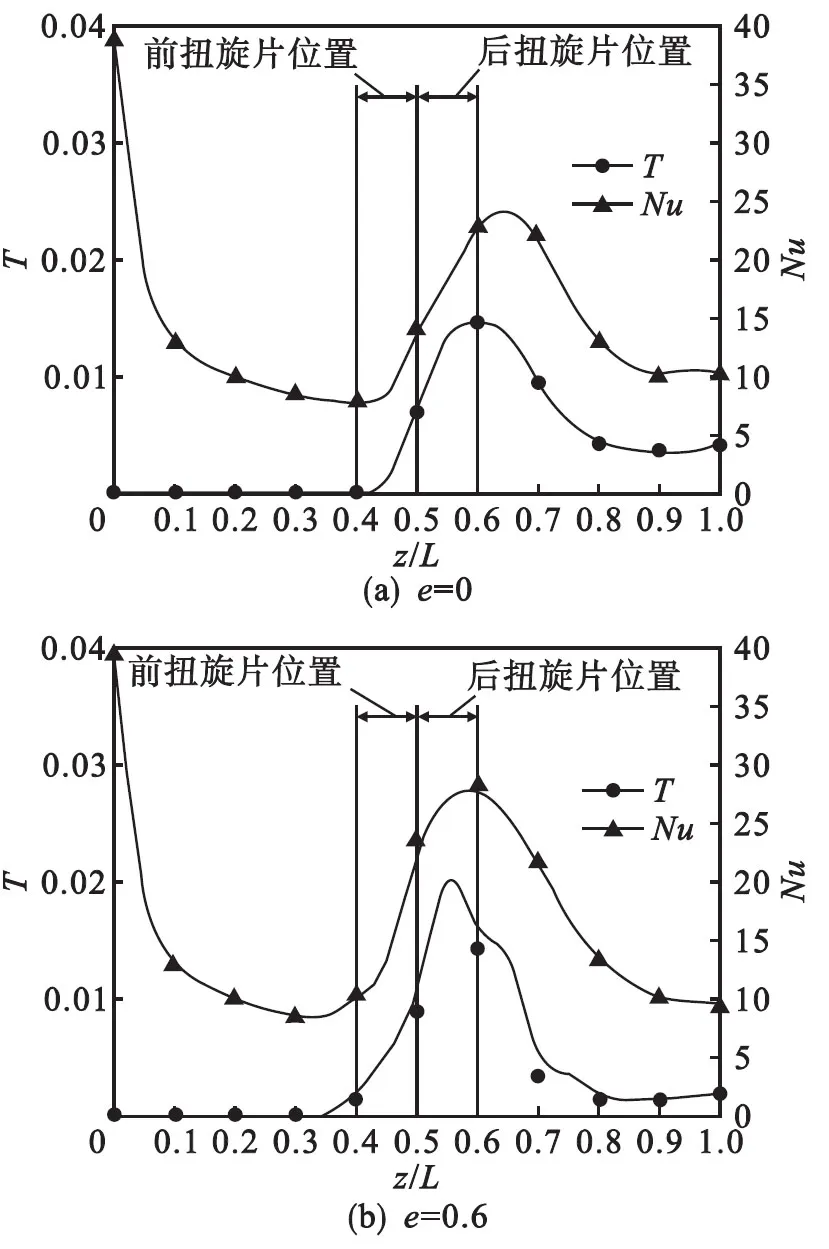
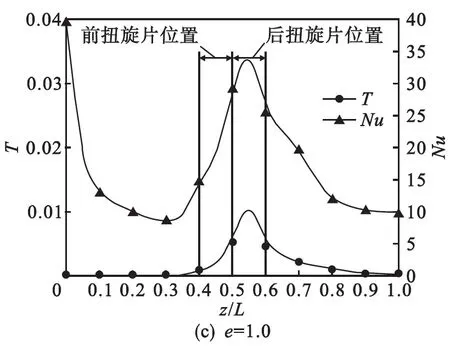
基于与前节同样的原因，本部分仍旧利用相对值反映径流数对努赛尔数的影响.相对努赛尔数定义与前节完全相同，而相对径流数表示为T/T0.其中，T0为理想径流数，利用管内二次涡流所形成的当量径向速度和轴向速度计算得到.假定扭旋片与管壁所形成的半圆形流道内，存在两个旋向相反的二次涡流，呈轴对称分布状态并与边壁相切，如图8所示.

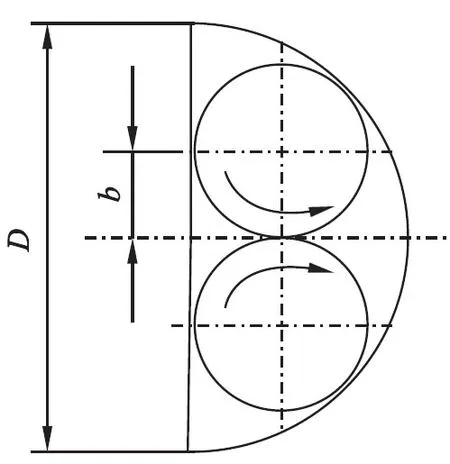
(5)

该式代表了较低的雷诺数下扭旋元件产生径向流动的能力，与长径比的平方成反比.

图9给出了相对径流数与相对努赛尔数对比关系曲线.由图9可以看出：相对径流数与相对努赛尔数沿轴向变化规律极其接近，相似程度甚至好于图6给出的相对旋流数与相对努赛尔数对比关系曲线；随着宽度比的增大，相对径流数和相对努赛尔数达到极值的轴向位置更为接近，且更为靠前.由此可见，径流数与旋流数均可以用于表征螺旋流传热强化能力，在分析过程中，两者同时使用能够起到校验作用.径流数除了可以用于螺旋流之外，也可用于错流射流研究过程，为射流传热强化提供一个定量参数.

3.3 雷诺数对旋流数与径流数的影响

3.1和3.2分析了Re=600情况下，旋流数和径流数轴向变化规律.为了分析雷诺数对旋流数与径流数的影响，本文在不同的雷诺数(Re=200～1800)及e=1.0结构下，求出了扭旋元件长度范围相对旋流数、相对径流数以及相对努赛尔数的平均值，其相互关系如图10所示.

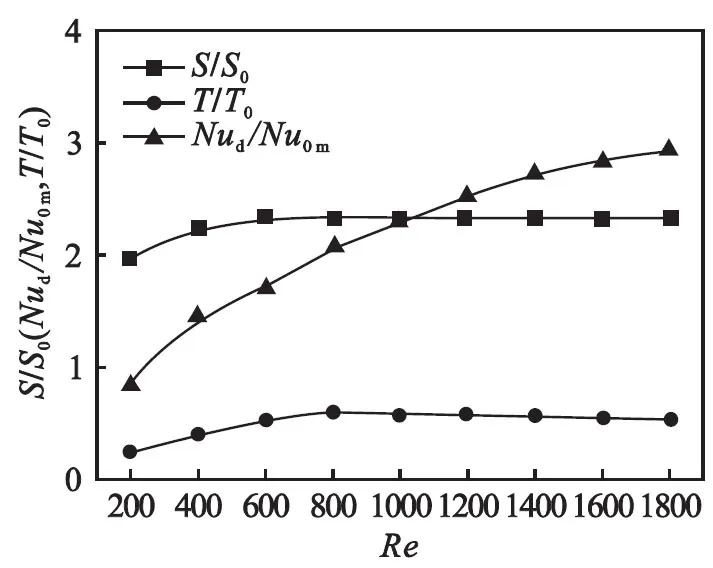
由图10可以看出：管内流体的努塞尔数随着雷诺数的增大而提高，说明流体轴向流速增大之后，周向速度和径向速度也相应增大，进而导致对流换热系数提高；相对旋流数和相对径流数在较小的雷诺数范围(Re≤800)随雷诺数增大而提高，而当雷诺数大于某值后(Re>800)几乎保持恒定，说明在扭旋元件长度范围内旋流的三维速度之间的相对值几乎保持恒定，与雷诺数关系微小.由此可见，旋流数和径流数的定义没能体现雷诺数对传热效果的影响，仅能反映换热管不同轴向位置传热系数的变化规律，因此，这两个参数有进一步改进的必要.

4 结 论

(1) 首次提出了表征螺旋流径向流动强度的“径流数”概念及其无量纲表达式，该参数体现了流体径向流动动能与轴向流动动能之比，与传统的“旋流数”相比，其与努塞尔数变化规律具有更好的吻合度.

(2) 管内流体在扭旋元件作用下，相对努塞尔数与相对旋流数、相对径流数在换热管轴向方向呈现相同的变化规律，在扭旋元件前缘前一定距离开始快速上升，在扭旋元件后缘一定距离开始快速下降，这两段距离均为半个扭旋片长度左右.

(3) 管内努塞尔数随着雷诺数的增大而提高，而旋流数及径流数在较小的雷诺数范围内(Re≤800)随着雷诺数的增大而提高，但当雷诺数大于某一定值后(Re>800)均保持恒定，这种现象说明旋流数和径流数虽然能够反映换热管不同轴向位置的变化规律，但是没能体现出雷诺数对传热效果的影响，这两个参数有进一步改进的必要.

(4) 管内螺旋流的旋流特性能够表征管内流体的传热性能，通过扭旋元件旋流特性的研究在一定程度上可以替代传热特性研究，缩短扭旋元件的研发周期.