FPSO单点系泊系统导缆器疲劳寿命预报方法
2019-04-20乐京霞王思宇刘玉亮陈鹏飞姚国全
乐京霞,王思宇,刘玉亮,陈鹏飞,姚国全
1武汉理工大学交通学院,湖北武汉430063
2东京大学工学院,日本东京113-8656
3上海勘测设计研究院有限公司,上海200434
0 引 言
近年来,随着海洋油气开发逐渐由浅海走向深海,适用于深海的浮式生产储油轮(Floating Production Storage and Offloading,FPSO)得到广泛应用。导缆器属FPSO系泊系统中的重要部分,主要用于改变系泊缆的走向,维持船舶或者平台的系泊状态。若导缆器损坏,易引起船舶运动状态的突然改变,对船上设备及船员安全具有较大影响。特别是在大风大浪的情况下,导缆器失效有可能导致船舶或者平台脱离系泊地,从而对船员生命及财产造成巨大影响。2010年,发现服役于英国北海的FPSO单点系泊系统的导缆器存在损坏问题[1]。目前,国内服役的FPSO虽然还未出现导缆器损坏的情况,但若在服役阶段发现导缆器损坏然后再对其进行置换,工作量将会非常大。因此,若能在导缆器的选用阶段通过数值计算方法对其疲劳寿命进行预报,将对系泊系统的设计大有帮助。
导缆器在工作时会承受系泊缆的作用力,在风、浪、流的联合作用下,系泊缆对导缆器的载荷就是一个不断变化的动载荷,容易引起结构的疲劳失效。李欣等[2]对FPSO单点系泊系统进行动力分析,并与模型试验结果进行对比,验证了动力方程与计算程序的可行性。许鑫等[3]针对波浪耦合作用对单点系泊系统的影响进行了研究,发现考虑波—流耦合作用时船体的水平位移与系泊缆的受力均会增大。Ma和Duan[4]针对海洋平台与系泊系统之间的耦合响应进行了研究。Yue和党之凡等[5-6]运用断裂力学方法,针对疲劳裂纹的扩展问题进行了研究。长期以来,国内外学者以及相关机构比较关注的都是系泊缆的布置和疲劳寿命,而针对系泊缆导向装置导缆器的研究则比较缺乏,可供参考的标准和规范也较少。挪威船级社(DNV)的海洋结构疲劳规范[7]针对导缆器的支撑结构提出了强度要求,并要求导缆孔或带滚柱的导缆器需具有足够大的开口,以便相关部件能顺利通过导缆装置。DNV的系泊定位规范[8]对导缆器材料的钢级、滚轮直径大小以及系缆状态下的设计载荷予以了规定,要求导缆器滚轮选用高强度钢,并且导缆器的使用寿命最少为20年,但并未给出直接计算指南。
本文将以研发中的旋转式导缆器为研究对象,提出一种预报其疲劳寿命的方法。首先,采用时域耦合计算理论计算FPSO单点系泊系统导缆器在南海百年一遇极限海况下承受的外载荷,通过有限元法分析在极端外载荷条件下导缆器的结构强度是否满足要求;然后,根据有限元计算结果计算其应力集中系数;最后,基于时域耦合分析法和有限元法,结合FPSO工作海域波浪散布图,得到各海况下FPSO单点系泊系统导缆器处缆绳张力时间历程和导缆器热点应力幅值时间历程。得到导缆器热点应力幅值时间历程后,再使用雨流计数法计数,并基于S-N曲线和Miner线性疲劳累积损伤理论对导缆器的疲劳寿命进行预报。
1 计算理论
1.1 时域耦合计算理论
浮体系泊于海洋会受到海洋环境载荷的作用,环境载荷中除波浪载荷外,还有风载荷和流载荷。时域下的波浪载荷是在频域计算的基础上,利用卡明斯脉冲理论和傅里叶变换而得到。风、流载荷最精确的计算结果是通过风洞实验测得,在没有风洞实验资料的前提下,可根据经验公式估算。除海洋环境载荷的作用外,浮体还将受到系泊系统提供的回复力的作用。系泊系统的回复力可通过求解系泊缆的动力学微分方程获得。所以,在已知水动力系数、波浪载荷和风、流载荷,以及系泊回复力的基础上,系泊系统的时域耦合运动方程可表达为[9]

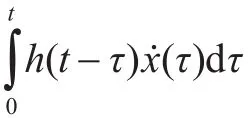
1.2 古德曼公式
由于雨流计数未考虑平均应力对疲劳寿命的影响,所以需要对雨流计数时采用的名义应力进行修正。目前,修正的方法有很多,其中,古德曼(Goodman)修正公式因计算简单和偏保守的估计而被广泛应用。
古德曼修正满足以下关系式:

式中:Sa为应力幅值;SNF为材料的疲劳强度;Sm为平均应力;Su为材料的极限抗拉强度。
2 FPSO单点系泊系统时域耦合分析
2.1 FPSO船舶参数
本船为无推进船舶,特点是单甲板、双底双舷侧,无球艏、无艏楼,12点锚泊定位,艏部设置有岛礁连接浮桥。作业海域为中国南海,其水深约1 000 m。船舶的疲劳寿命50年,载重量150 000 t。主尺度参数如表1所示。

表1 FPSO主尺度Table 1 The main dimensions of FPSO
2.2 FPSO单点系泊系统
FPSO采用内转塔式单点系泊系统进行定位。系泊系统共有12根系泊缆绳,分为3组,每组4根,每组系泊缆之间的夹角为120°,每组内相邻2根系泊缆绳之间的夹角为5°。系泊缆绳由3部分组成:靠近船体和近底部分为钢缆;中间部分为聚酯缆绳。系泊布置如图1所示,缆绳参数如表2所示。

图1 系泊布置图Fig.1 Mooring arrangement diagram

表2 系泊缆绳参数Table 2 Mooring cable parameters
2.3 环境条件
根据美国船级社(ABS)的规范[10]规定,FPSO必须按照100年重现期的波浪+相应的风和流,或者100年重现期的风+相应的波浪和流这两种生存环境组合条件之一进行设计。该FPSO作业于中国南海海域,水深1 000 m,海洋环境选择为南海百年重现期有台风的海况,海况参数如表3所示,波浪谱选用JONSWAP谱,风、浪、流的方向均为180°,即艏迎浪方向。

表3 环境条件Table 3 Environment condition
2.4 结果分析
使用水动力软件AQWA对FPSO单点系泊系统进行动力分析。在风、浪、流同向且均在艏迎浪方向条件下,FPSO纵荡运动响应和#1缆绳张力具有较大值,统计值如表4所示。

表4 FPSO最大纵荡运动响应值和缆绳张力值Table 4 The maximum values of FPSO surge motion response and cable tension
根据ABS规范[10],深水作业的FPSO的水平位移不得超过水深的10%;美国石油协会(API)规范[11]规定,在完整系泊工况下,采用动态法计算系泊缆绳的张力时安全因子取为1.67。表4的计算结果表明,该系泊系统设计是安全、可靠的。
本文研究的FPSO纵荡运动响应时间历程和#1缆绳张力的时间历程分别如图2和图3所示。

图2 纵荡运动响应时历曲线Fig.2 Time history curve of surge motion response
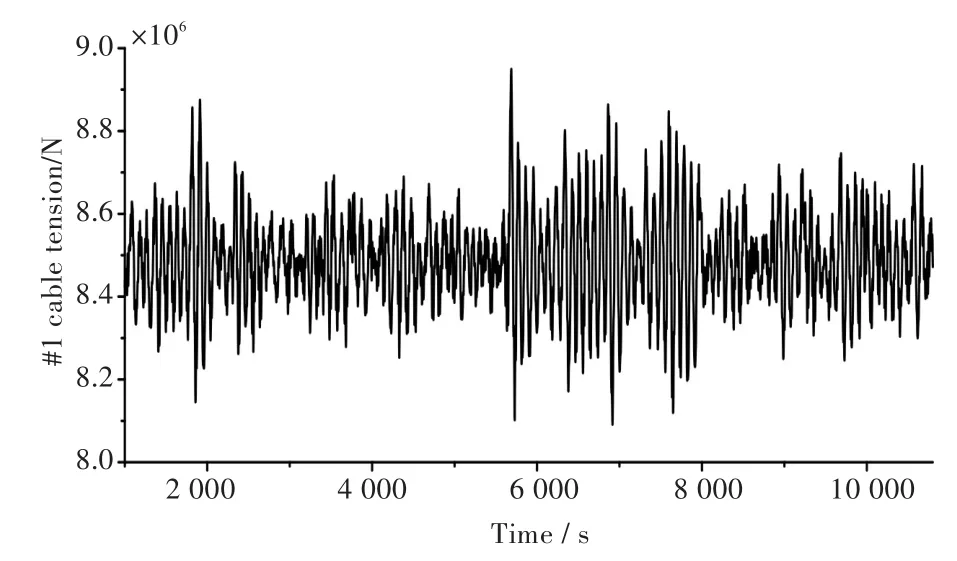
图3 #1缆绳张力时历曲线Fig.3 Time history curve of#1 cable tension
3 导缆器结构强度分析
3.1 有限元模型
处于研发中的旋转式导缆器高3.87 m,长3.68 m,板厚30,40 mm。导缆器与系泊缆绳接触的部位是一个滚轮,该滚轮连接在圆轴上,将受力传递到导缆器。系泊系统导缆器布置如图4所示,导缆器侧视图如图5所示。为简化计算,忽略计算模型中的滚轮,直接将载荷施加在圆轴上。计算时,将导缆器与FPSO的接触部分进行约束,载荷直接加载在圆轴上。
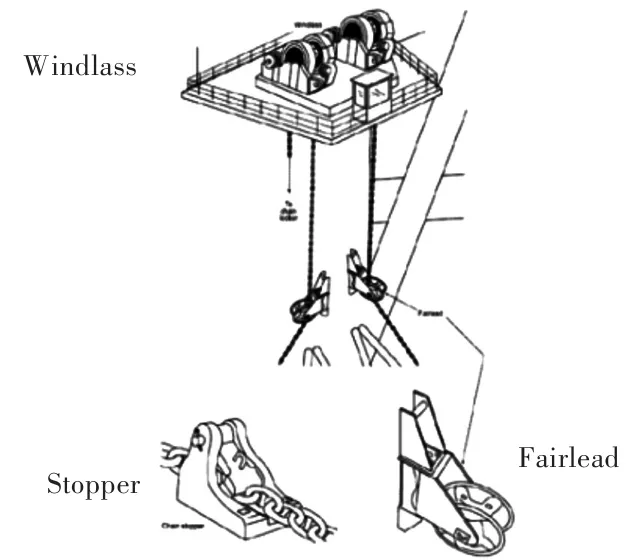
图4 系泊系统导缆器布置图Fig.4 Arrangement of fairlead of mooring system
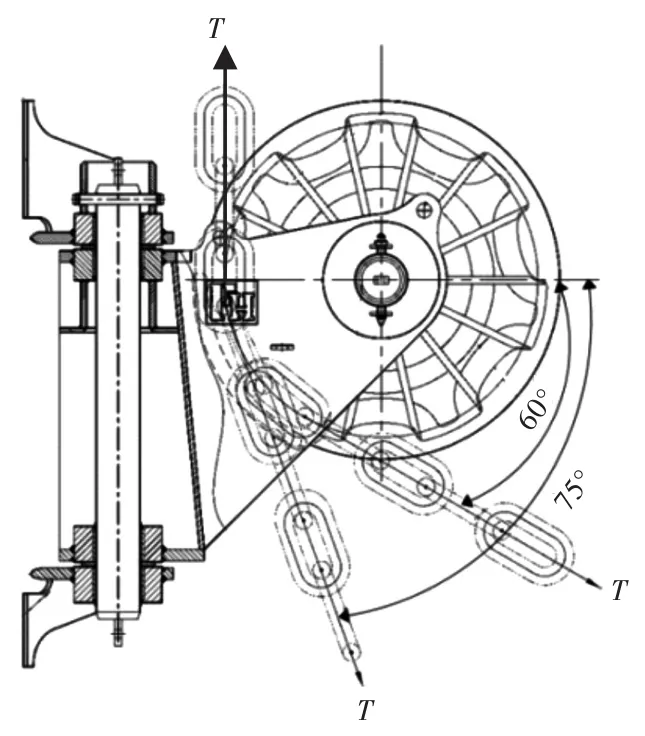
图5 导缆器侧视图Fig.5 Side view of fairlead
3.2 结果分析
导缆器在改变系泊缆绳方向的同时,也承受着来自系泊缆绳的压力。以FPSO百年一遇极端设计条件得到的#1系泊缆绳张力最大值作为外载荷,对导缆器进行强度分析。假设系泊缆绳的拉力为T,缆绳夹角与导缆器所受合力的关系图如图6所示。根据DNV的系泊定位规范[8],系泊缆绳在导缆器滚轮之间的夹角范围为120°~150°(图6所示红色范围)。如图7所示的导缆器滚轮受力图,当导缆器滚轮之间的夹角为120°时,合力大小为T,而当导缆器滚轮之间的夹角为150°时,合力大小为0.518T,可见该夹角对载荷影响很大。
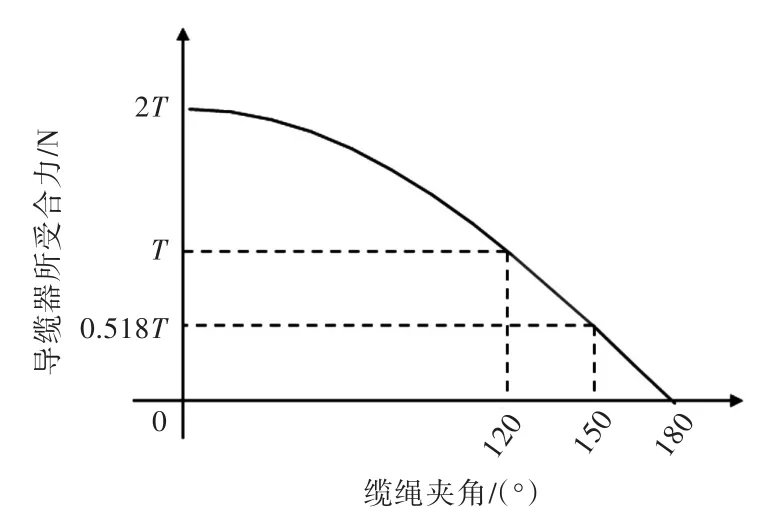
图6 缆绳夹角与导缆器合力关系图Fig.6 The relationship between cable angle and resultant force of fairlead
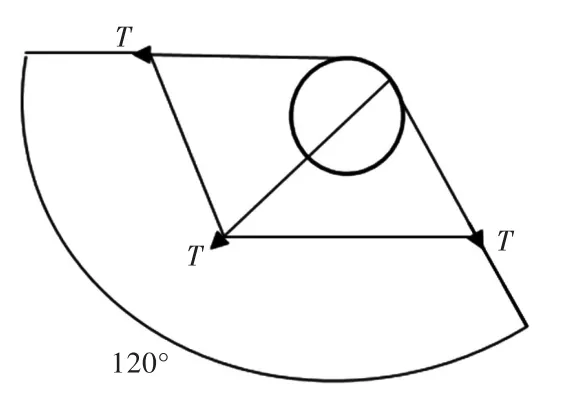
图7 导缆器滚轮受力示意图Fig.7 The force diagram of fairlead's roller
基于偏安全考虑,根据DNV规范[8]给出的夹角范围,在进行强度分析时导缆器滚轮之间的夹角取为120°。强度计算得到的导缆器应力云图如图8所示。由图可见,最大等效应力为367.745 MPa,应力最大点出现在侧板与前轴相交处。导缆器材料为低合金高强度钢Q420,屈服强度为420 MPa,最大等效应力小于0.9倍屈服强度。计算结果表明,导缆器的结构强度满足要求。
4 应力集中系数
所谓应力集中,是指结构由于缺口或截面积的变化而使得这些部位的应力变大的现象。应力集中是结构疲劳强度的薄弱环节,任何结构或零件几乎都存在应力集中。根据图8所示,疲劳点位于应力集中区域,所以在进行疲劳分析时必须考虑应力集中系数(SCF)。局部应力可由下式求出:

式中:σmax为局部位置的最大应力;σnominal为导缆器的名义应力。
因该导缆器现仍处于设计阶段,所以有限元计算是一种比较有效且可行的用来计算其应力集中系数的方法。
4.1 计算流程
计算导缆器应力集中系数的关键是准确得到最大局部应力和名义应力。缺口处最大应力可以由整体建模的有限元分析方便地得到,最大应力可取最大等效应力,名义应力则取净面积上的平均应力,最后根据式(3)计算得到应力集中系数。有限元计算导缆器应力集中系数流程如图9所示。

图9 计算流程图Fig.9 Calculational flow chart
4.2 应力积分
由主应力性质和载荷方向,确定积分路径如图10所示。积分路径垂直于外载荷方向,并根据有限元计算结果,选取最大主应力进行积分。

图10 积分路径Fig.10 Path of integration
应力积分的目的是求出净截面上的平均应力,即名义应力。若要求解得到图10中应力分布的平均值,首先应对图11中的应力曲线进行路径积分,然后再将积分值除以路径长度,即可得出净面积上的名义应力。如图12所示,曲线的峰值为117.31 MPa·m,即沿路径的应力积分值。
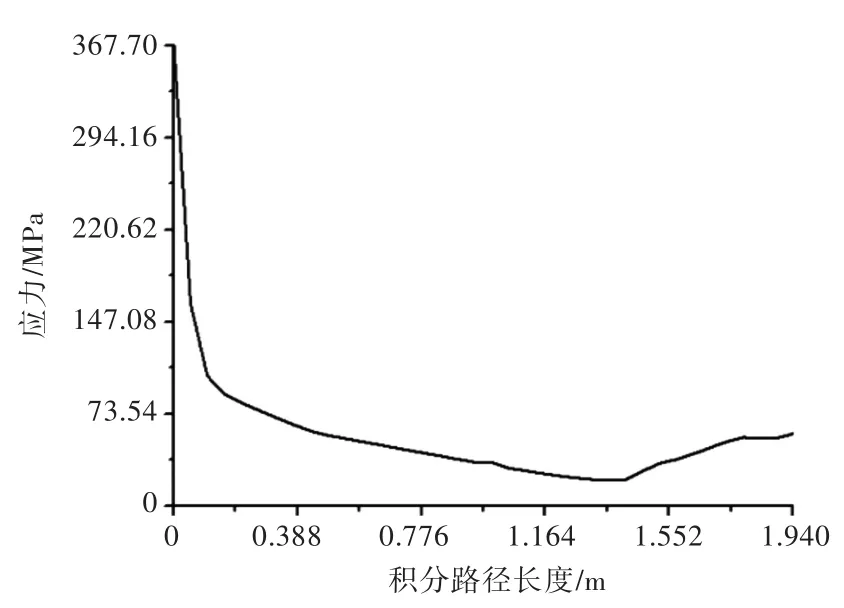
图11 路径上的应力分布Fig.11 Stress distribution along the path
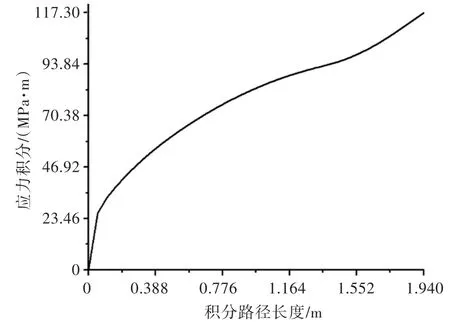
图12 路径上的应力积分Fig.12 Stress integral along path
4.3 应力集中系数求解
基于应力积分值,便可根据式(4)求出名义应力(单位:MPa)。
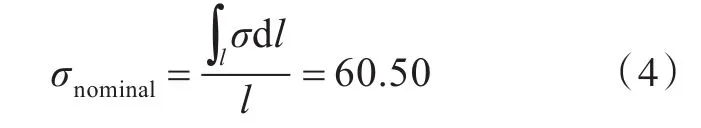
式中:l为路径长度;∫lσdl为上述应力沿路径的积分值。
根据应力集中系数的定义,便可求得导缆器的应力集中系数。

5 导缆器的疲劳寿命预报方法
5.1 计算说明
疲劳载荷主要由波浪载荷引起,在疲劳寿命评估中波浪的长期状态可以认为是由多个短期海况序列组成,每个短期海况可以用波高、周期、波谱、流速和风速等参数描述,且每个短期海况都有其确定的发生概率P。本文研究的FPSO长期作业于中国南海S4海域,该海域的波浪散布图如表5所示(表中,TZ为平均跨零周期)。根据波浪散布图,将长期海况离散成总计64种短期海况;波浪谱采用JONSWAP谱,谱峰升高因子γ=3.3;风采用定常风,风、浪、流均为180°方向。
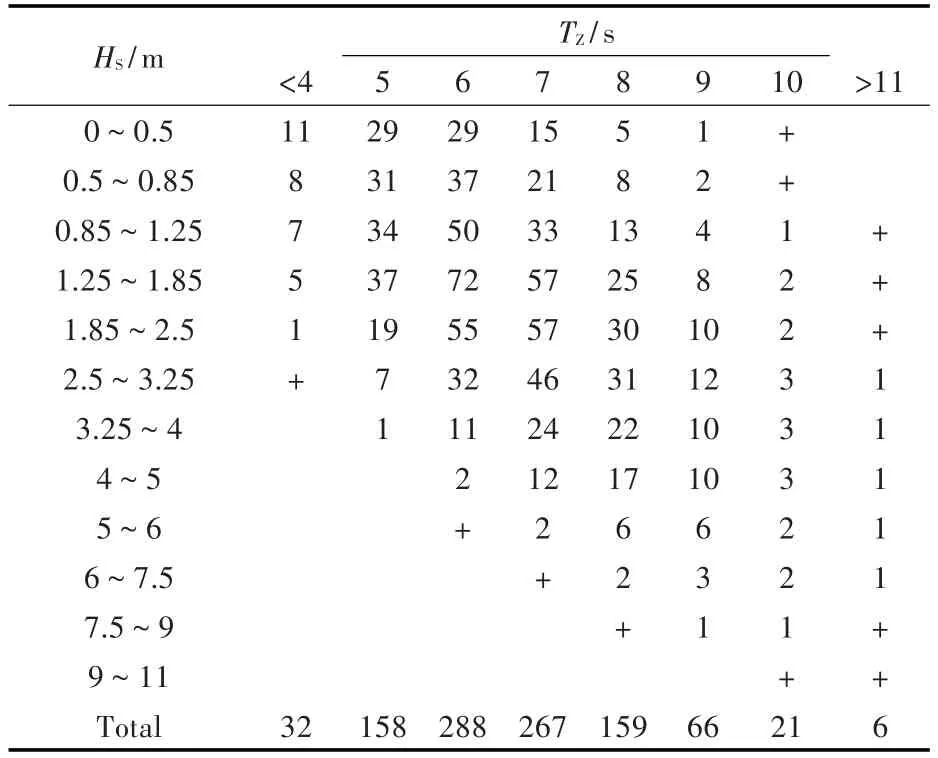
表5 中国南海S4海域波浪散布图Table 5 Wave scatter diagram of S4 area in South China Sea
基于时域耦合计算方法,可计算出上述64种短期海况下#1系泊缆张力的时间历程;基于强度计算,可建立#1系泊缆张力与导缆器应力之间的关系如图13所示。所以,通过时域耦合分析方法和有限元法,即可得到64种短期海况下导缆器的应力时间历程。导缆器应力经古德曼公式修正后,运用雨流计数对其时间历程进行处理,即可生成疲劳载荷谱。根据导缆器材料以及应力集中系数等参数,疲劳S-N曲线采用DNV经修正的非管节点S-N曲线中的D曲线[7],曲线如图14所示。
一水平中央泵房排水系统核定能力为16.41万t/a,二水平中央泵房排水系统核定能力为342.97万t/a,三水平中央泵房排水系统核定能力为173.01万t/a,矿井排水能力核定为532万 t/a。

图13 #1系泊缆张力与导缆器应力之间的关系Fig.13 The relationship between#1 cable tension and fairlead stress

图14 S-N曲线Fig.14 S-N curves
5.2 结果分析
64种短期海况下,#1系泊缆对应的导缆器疲劳累积损伤计算结果如表6所示。表中的疲劳累积损伤是基于时域耦合分析时长3 h得到的,一年内总共有2 920个3 h,所以#1系泊缆一年内的总累积损伤为表6计算结果的2 920倍。
根据Miner线性疲劳累积损伤理论,导缆器一年内的总累计损伤度D为
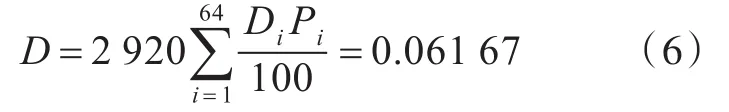
在不考虑结构安全系数的情况下,当结构疲劳累积损伤度D>1时,认为结构发生了疲劳破坏,或者不能满足疲劳强度设计要求。根据计算结果,导缆器一年内的总疲劳累积损伤度为0.06 167,疲劳寿命为16.21年,可以作为导缆器检修更换周期确定的依据。
6 结 论
本文以某尚处于研发中的旋转式导缆器作为研究对象,基于时域耦合分析方法和有限元法,提出了一种导缆器疲劳寿命预报方法。通过该方法,当系泊体的系泊方案和作业海域已定时,即可对系泊方案中选定的导缆器疲劳寿命进行预报,并以此判断选用的导缆器在整个服役阶段是否存在疲劳破坏的可能性,从而为系泊系统设计选择导缆器提供参考。主要结论如下:
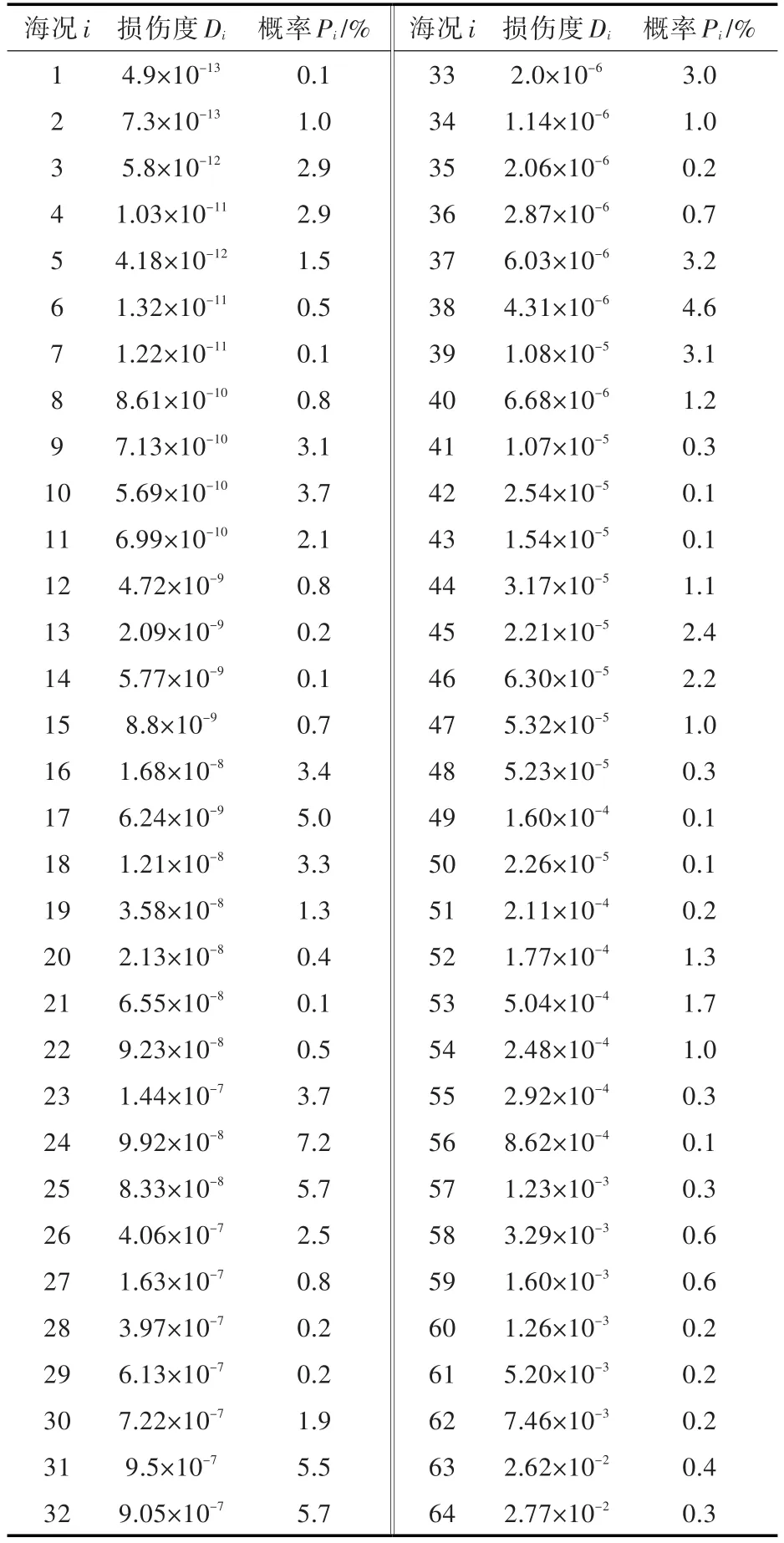
表6 导缆器疲劳累积损伤表Table 6 Fatigue damage of the fairlead
1)通过FPSO系泊系统时域动力学分析,可得到缆绳张力时间历程,再通过有限元计算将其转换为导缆器名义应力时间历程,并以此为基础估算导缆器的疲劳寿命,便可为导缆器疲劳寿命预报提供一种可参考的方法。
2)本文所研究的导缆器结构复杂,故无法通过规范或手册获取其应力集中系数。通过有限元方法计算导缆器的应力集中系数,在导缆器设计初期可为疲劳寿命估算提供依据。
