小水线面三体船与细长型三体船剩余阻力对比分析
2019-04-20张明霞韩兵兵卢鹏程
张明霞,韩兵兵,卢鹏程
大连理工大学船舶工程学院,辽宁大连116024
0 引 言
21世纪是海洋的世纪,海洋资源的勘测和开发,以及海军装备发展等对船舶设计和船舶性能提出了更高的要求。三体船型作为一种新型的高性能船型,引起了造船界的广泛关注[1-3]。小水线面三体船(TriSWACH)由1个小水线面型主体和2个侧体构成,侧体的排水量一般不超过主体或总排水量的10%[4-5],主体在水面附近为薄型立柱,水线面下设置有潜体。该船在继承细长型三体船优点的基础上,具有更小的波浪附加阻力和更好的耐波性[6],其在相当的船长条件下可以较多地增加排水量,提供更多有效载荷[7],在民用和军用领域具有广泛的应用前景[8-10]。作为排水型船舶,TriSWACH在中、高速时其剩余阻力是总阻力的重要成分,不同侧体布局位置导致的兴波干扰会对剩余阻力产生显著影响。合理布置侧体位置,以产生有利的兴波干扰,降低剩余阻力,是提高TriSWACH快速性的重要手段。在国外,Boulgy[11]和Smith[12]分别针对小水线面三体反潜护卫舰和小水线面三体近海巡逻艇进行了概念设计。McDonald等[13]对 TriSWACH 侧体舷侧内倾角在15°~40°范围内的阻力变化规律予以了研究。在国内,顾敏童等[6]通过模型试验,研究了潜体横剖面为椭圆形的TriSWACH的总阻力特征,并与船长相当、排水量较小的细长型三体船总阻力试验结果进行了对比,试验表明,TriSWACH的总阻力要优于细长型三体船的总阻力,但未考虑潜体横剖面形状因素对阻力性能的影响。刘嵩[14]利用Fluent软件,对傅汝德数 Fr=0.443~0.553、潜体横剖面为圆形和椭圆型的TriSWACH在规则波中的总阻力数值进行了计算,结果表明,潜体形状为圆形的TriSWACH的总阻力较小。该研究中的速度范围具有一定的局限性,且未对二者的剩余阻力进行分析比较。
目前,国内外对于细长型三体船的剩余阻力问题已进行了深入研究[15],但针对TriSWACH剩余阻力预报的资料却很少。按照通常处理船体阻力的方法,将三体船总阻力分为摩擦阻力和剩余阻力两部分。其中,摩擦阻力按单体船ITTC-57方法计算,而剩余阻力主要取决于片体间的兴波干扰,因此受三体船侧体布局的影响较大。本文TriSWACH阻力研究的重点是探究剩余阻力随航速及侧体布局变化的规律。在阻力研究方法中,船模试验结果最为可靠,但完成全部方案的船模试验周期较长、费用昂贵。现今,CFD技术在船舶阻力预报方面已取得显著成果,为此,本文将利用STAR-CCM+平台,在已验证该平台对三体船粘性流场阻力数值计算具有可靠性的基础上,研究系列航速下,不同侧体位置时,片体间兴波干扰对TriSWACH剩余阻力的影响,用以为一定航速阶段内阻力最优时的侧体布置提供一定的工程借鉴。
1 模型及方案设计
1.1 船型变换
以文献[16]中的细长型三体船模为依据,基于船长、船宽和排水量不变的原则,将细长型三体船模型线变换为TriSWACH船模型线,船模横剖面示意图如图1和图2所示。TriSWACH船模主尺度参数如表1所示,实船和模型的缩尺比λ=25。

图1 细长型三体船模横剖面示意图[1]Fig.1 Schematic diagram of cross-section of slender trimaran model[1]

图2 TriSWACH船模横剖面示意图Fig.2 Schematic diagram of cross-section of TriSWACH model

表1 TriSWACH船模主尺度参数Table 1 Main dimensions of the TriSWACH model
船体坐标系如图3所示。其中,x轴沿船长方向指向主体艏部为正,y轴沿船宽方向指向主体左舷为正。侧体中心线与主体中心线间的横向跨距为a,a始终为正值;侧体船舯与主体船舯的纵向偏距为b,当侧体位于主体船舯之前时,b为正值;当侧体位于主体船舯之后时,b为负值。
1.2 建模及网格划分
通过文献[17]中有关细长型三体船阻力计算值与试验值的对比发现,STAR-CCM+平台在计算三体船阻力方面具有一定的可靠性。假设忽略细长型三体船与小水线面三体船的船型差异,因此,可以应用其计算TriSWACH船模阻力数值。

图3 船体坐标系Fig.3 Ship hull coordinate system
首先,基于CATIA平台进行TriSWACH船体及计算流域的建模。TriSWACH三维视图如图4所示。由于TriSWACH为对称船型,因此本文取左舷一侧进行计算。计算流域为长方体,入口取主体艏部向上游延伸至3倍主体船长处,出口取艉部向下游延伸至5倍主体船长处;区域右侧边界为对称面(主体纵舯剖面),区域左侧边界为由对称面向左舷方向延伸1倍主体船长;计算流域高约2倍主体船长,空气层厚度约为0.75倍主体船长。

图4 TriSWACH三维视图Fig.4 The 3D view of TriSWACH
利用STAR-CCM+平台自动划分流域网格。在设置网格相关参数时,对船艏、艉处和自由液面处的网格进行加密处理,然后再以一定的梯度外推,以满足计算需要。计算流域空间采用切割六面体网格,共划分为336 821个网格单元。TriSWACH船体内部切割体网格及流域网格划分分别如图5和图6所示。计算流域的边界条件分别设置为速度进口、压力出口、对称面和壁面,如图7所示。

图5 船长方向内部切割体网格Fig.5 Internal cutting meshses in longitudinal direction

图6 流域表面网格划分图Fig.6 Surface mesh partition of fluid region

图7 流域边界条件Fig.7 Boundary conditions of fluid region watershed
1.3 侧体布局方案
与文献[16]中的速度、侧体位置方案设置相同,选择侧体3个纵向位置、2个横向位置共6种不同的侧体位置方案。每种方案分别计算Fr=0.105,0.234,0.338,0.494,0.598,0.701这 6种航速下的阻力数值。侧体位置方案如表2所示,其中L为船长。

表2 三体船模侧体位置方案[16]Table 2 Side-hulls scheme of trimaran model[16]
2 计算及结果比较
2.1 摩擦阻力系数计算
假设相同航速、不同侧体布局位置时三体船的摩擦阻力不发生变化,根据傅汝德阻力分类方法,将总阻力Rt分为摩擦阻力Rf和剩余阻力Rr两部分。采用文献[18]中的摩擦阻力计算ITTC-57方法计算得出系列航速,固定侧体布局位置时的细长型三体船、TriSWACH的整体摩擦阻力系数Cf如图8所示。
2.2 剩余阻力系数计算

图8 三体船整体摩擦阻力系数Fig.8 Overall friction resistance coefficients of trimaran
不同航速、侧体位置方案的细长型三体船总阻力Rt0由模型试验[16]得出,对应航速、侧体位置方案的TriSWACH总阻力Rt1利用STAR-CCM+平台,采用标准k-ε湍流模型、流体体积(VOF)法数值计算得出,总阻力数值见文献[17]。
剩余阻力系数计算结果分别如表3~表8所示。表中,Cr0为细长型三体船剩余阻力系数,Cr1为TriSWACH剩余阻力系数。

表3 Fr=0.105时的剩余阻力系数Table 3 Residual resistance coefficients when Fr=0.105

表4 Fr=0.234时的剩余阻力系数Table 4 Residual resistance coefficients when Fr=0.234

表5 Fr=0.338时的剩余阻力系数Table 5 Residual resistance coefficients when Fr=0.338

表6 Fr=0.494时的剩余阻力系数Table 6 Residual resistance coefficients when Fr=0.494

表7 Fr=0.598时的剩余阻力系数Table 7 Residual resistance coefficients when Fr=0.598

表8 Fr=0.701时的剩余阻力系数Table 8 Residual resistance coefficients when Fr=0.701
2.3 剩余阻力比较
首先,将细长型三体船剩余阻力系数Cr0和TriSWACH剩余阻力系数Cr1绘制成曲线,分别如图9和图10。然后,将剩余阻力系数曲线分成不同的傅汝德数区间分别进行讨论,如图11~图16所示。
从图9和图10中可以看出:
1)TriSWACH的剩余阻力系数Cr1相比细长型三体船的剩余阻力系数Cr0普遍较小。
2)细长型三体船的剩余阻力系数曲线波峰值为7.467,曲线波峰出现在Fr=0.35附近;TriSWACH的剩余阻力系数曲线波峰值为2.723,曲线波峰出现在Fr=0.5附近。这说明TriSWACH航行时波高较小。

图9 细长型三体船模剩余阻力系数[17]Fig.9 Residual resistance coefficients of slender trimaran[17]

图10 TriSWACH剩余阻力系数Fig.10 Residual resistance coefficients of TriSWACH

图11 Fr=0.1~0.3时细长型三体船模剩余阻力系数Fig.11 Residual resistance coefficients of slender trimaran when Fr=0.1~0.3

图12 Fr=0.1~0.3时TriSWACH剩余阻力系数Fig.12 Residual resistance coefficients of TriSWACH when Fr=0.1~0.3

图13 Fr=0.3~0.5时细长型三体船模剩余阻力系数Fig.13 Residual resistance coefficients of slender trimaran when Fr=0.3~0.5

图14 Fr=0.3~0.5时TriSWACH剩余阻力系数Fig.14 Residual resistance coefficients of TriSWACH when Fr=0.3~0.5

图15 Fr=0.5~0.7时细长型三体船模剩余阻力系数Fig.15 Residual resistance coefficients of slender trimaran when Fr=0.5~0.7

图16 Fr=0.5~0.7时TriSWACH剩余阻力系数Fig.16 Residual resistance coefficients of TriSWACH when Fr=0.5~0.7
从图11~图16中可以看出:
1)当Fr=0.1~0.3时,侧体位置改变对阻力的影响较小,其原因是低速时兴波阻力占总阻力的成分小,片体间兴波干扰的影响较小。相比而言,对于2种船型,方案1的剩余阻力系数较小,说明低速时侧体布局在主体前部能降低阻力,最大降阻可达10.66%。
2)当Fr=0.3~0.5时,Cr1曲线与Cr0曲线出现了相反的变化趋势,分析其原因,是随着航速的增大,试验中细长型三体船喷溅阻力的影响也随之增大,从而导致波峰提前出现[16]。在该航速范围下,TriSWACH的方案3和方案6的剩余阻力较小,说明将侧体布置在主体后部更有利于减阻,最大减阻可达17.95%。对比方案1和方案4、方案3和方案6的减阻效果,可知相比纵向位置,横向位置变化对阻力的影响较小。
3)当Fr=0.5~0.7时,TriSWACH的方案3和方案6,即侧体布置在主体后部时,对兴波产生了显著的有利干扰,有效降低了剩余阻力,最大降阻可达24.71%。
4)当Fr=0.3~0.7时,TriSWACH的Cr1曲线分布具有一定的规律性,曲线的排列顺序随着侧体纵向位置的后移逐渐降低。
2.4 阻力成分占比及变化梯度分析
结合文献[17]中得到的TriSWACH总阻力值,分析TriSWACH的摩擦阻力与剩余阻力在总阻力中的成分,如图17所示。同时,对比分析不同航速下TriSWACH相比细长型三体船的摩擦阻力增长梯度与剩余阻力降低梯度,如图18所示。其中,剩余阻力取各航速下6种侧体布局位置下计算得到的剩余阻力平均值。
从图17中可以看出,摩擦阻力占总阻力的49%~65%,剩余阻力占总阻力的35%~51%。在本文所研究航速范围内,当Fr=0.45~0.6时,剩余阻力占总阻力的比值高于摩擦阻力,除Fr=0.45~0.6外,摩擦阻力占总阻力的比值高于剩余阻力。由图18可以看出,相比细长型三体船,TriSWACH的摩擦阻力增长梯度范围为3%~17%,剩余阻力的降低梯度范围为18%~64%。由于摩擦阻力的增长梯度显著小于剩余阻力的降低梯度,导致TriSWACH的总阻力低于相同船长排水量时细长型三体船的总阻力。
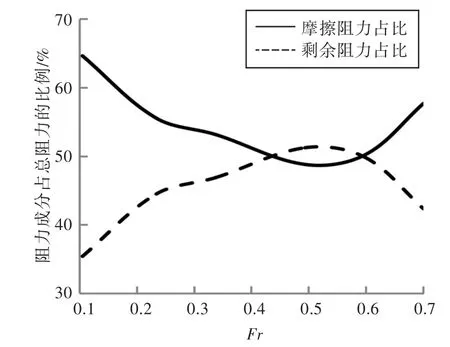
图17 阻力成分占比Fig.17 The proportion of resistance components

图18 阻力成分梯度变化Fig.18 Resistance component gradient change
3 兴波云图分析
首先,利用STAR-CCM+平台生成不同航速下TriSWACH主船体兴波云图;然后,将6种不同布局方案的侧体艏部位置绘制于主体兴波云图中,如图19~图24所示(图中,A~F分别代表方案1~方案6侧体艏部位置点)。由于侧体关于主体左右对称,故只给出了主体左侧的侧体位置。此外,为了更加直观地看出阻力最优时的侧体位置布局,绘制了TriSWACH在Fr=0.701下6种不同侧体位置的船体兴波云图,如图25~图30所示。其余航速下各方案的兴波云图此处省略。
结合TriSWACH的剩余阻力系数曲线,再对比图19~图24中的TriSWACH主体兴波云图,可以看出:
1)在同一航速下,当侧体艏部位于主体兴波波谷区域时,TriSWACH的阻力要小于侧体艏部位于主体兴波波峰区域时的阻力数值。

图19 Fr=0.105时的小水线面三体船主体兴波云图Fig.19 The wave-making contours of TriSWACH's main hull when Fr=0.105

图20 Fr=0.234时的小水线面三体船主体兴波云图Fig.20 The wave-making contours of TriSWACH's main hull when Fr=0.234

图21 Fr=0.338时的小水线面三体船主体兴波云图Fig.21 The wave-making contours of TriSWACH's main hull when Fr=0.338

图22 Fr=0.494时的小水线面三体船主体兴波云图Fig.22 The wave-making contours of TriSWACH's main hull when Fr=0.494

图23 Fr=0.598时的小水线面三体船主体兴波云图Fig.23 The wave-making contours of TriSWACH's main hull when Fr=0.598

图24 Fr=0.701时的小水线面三体船主体兴波云图Fig.24 The wave-making contours of TriSWACH's main hull when Fr=0.701

图25 方案1的小水线面三体船主体兴波云图Fig.25 The wave-making contours of TriSWACH's main hull(scheme 1)

图26 方案2的小水线面三体船主体兴波云图Fig.26 The wave-making contours of TriSWACH's main hull(scheme 2)

图27 方案3的小水线面三体船主体兴波云图Fig.27 The wave-making contours of TriSWACH's main hull(scheme 3)

图28 方案4的小水线面三体船主体兴波云图Fig.28 The wave-making contours of TriSWACH's main hull(scheme 4)

图29 方案5的小水线面三体船主体兴波云图Fig.29 The wave-making contours of TriSWACH's main hull(scheme 5)

图30 方案6的小水线面三体船主体兴波云图Fig.30 The wave-making contours of TriSWACH's main hull(scheme 6)
2)随着航速的增大,主体兴波的最大波谷逐渐后移,并有向主体收缩的趋势,这也印证了阻力最优时图14和图16中方案3与方案6的曲线变化趋势。
3)通过对比Fr=0.701时6种侧体位置下的船体兴波云图,发现当侧体艏部位置变化到主体最大波谷处时,获得的阻力最小,从而与上述结论相互印证。
4 结 论
综合上述分析,得到以下结论:
1)TriSWACH的剩余阻力普遍小于相当船长排水量细长型三体船的剩余阻力。
2)通过阻力成分占比分析发现,在本文所研究的航速范围内,TriSWACH的摩擦阻力占总阻力的49%~65%,剩余阻力占总阻力的35%~51%。相比细长型三体船阻力,TriSWACH摩擦阻力的增长梯度要小于剩余阻力的降低梯度,因此,TriSWACH的总阻力小于细长型三体船的总阻力。可见,在中、高速航线状态下,影响TriSWACH总阻力的关键因素仍为不同片体兴波干扰后的剩余阻力。
3)从剩余阻力系数曲线可以看出,作为排水型船舶,TriSWACH的设计航速可在Fr=0.338~0.494区间内获得最佳减阻效果。此时,剩余阻力降低的梯度最大,当最优侧体位置位于主体艉部时,最大减阻可达17.95%。因此,可进一步深入研究该航速区间内的船体水动力性能。
4)在全航速范围内,TriSWACH侧体艏部位于主体兴波最大波谷区域时获得的整船体阻力最小,据此,可得出不同航速下侧体位置布局的最优方案,具有一定的工程指导意义。
本文在进行TriSWACH的阻力数值模拟时,未考虑浮态变化对阻力结果的影响,因此,对于高速时浮态变化对阻力结果的影响仍需进一步研究。
