自然语言形式分析的奠基力作
2019-04-19冯志伟周建
冯志伟 周建


摘 要:1957年,乔姆斯基《句法结构》出版,这是对结构主义的一系列基本原理提出的挑战,是自然语言形式分析的奠基力作,标志着语言学中的“乔姆斯基革命”的开始。此书着重阐述了形式语言理论和转换语法。在形式语言理论中,乔姆斯基将语言看成是一个抽象的数学系统。为了描写和解释语言现象,他论证了语法的生成能力,认为应该把语法看成是能生成无限句子的有限规则系统。在转换语法中,乔姆斯基认为,转换语法模型由直接成分层级、转换层级、语素音位层级三个层级构成。在运用转换规则时,具体的操作方式主要有调位、复写、插入、消去,转换使语法具有更强的解释力。
关键词:乔姆斯基;《句法结构》;形式语言理论;转换语法
如果说,索绪尔语言学说的提出是语言学史上哥白尼式的革命,那么,乔姆斯基(N.Chomsky,1928— )的转换生成语法的提出,则是语言学史上的又一次划时代的革命,即“乔姆斯基革命”。
1916年索绪尔《普通语言学教程》的出版,开辟了现代语言学的新纪元,而1957年乔姆斯基《句法结构》的出版(Chomsky,1957),是对结构主义的一系列基本原理提出的挑战,标志着语言学中的“乔姆斯基革命”的开始。这场革命直到今天还没有完结(冯志伟,1982)。
《句法结构》一书出版已经60年了,这是一本对于现代语言学有重要影响的著作,也是自然语言形式分析的奠基力作,特写此文以志纪念。
一、乔姆斯基与《句法结构》
1928年12月7日,乔姆斯基出生于美国费城。他的父亲威廉· 乔姆斯基(William Chomsky)是一个希伯来语学者,曾写过《大卫·金西的希伯来语法》(Davis Kimhis Hebrew grammar)一文。幼年的乔姆斯基(他的名字叫诺阿姆,即Noam Chomsky)在父亲的熏陶下,就爱上了语言研究工作。1947年,他结识了美国描写语言学“后布龙菲尔德学派”的代表人物、著名语言学家海里斯(Z.Harris,1909—1992)。在研读了海里斯《结构语言学方法》(Method in Structural Linguistics)之后,他被海里斯那种严密的研究方法深深地吸引住,几乎到了心醉神迷的程度。从此,他立志以语言学作为自己毕生的事业,进入海里斯执教的宾夕法尼亚大学,专攻语言学。
乔姆斯基是熟悉希伯来语的,掌握了《结构语言学方法》的基本原理之后,他试图用海里斯的方法来研究希伯来语,但所获甚微。于是,他决定把海里斯的方法作适当的调整,建立一种形式语言理论,采用递归的规则来描写句子的形式结构,从而使语法获得较强的解释力。
从1947年到1953年,乔姆斯基花了整整六年时间来从事这项研究。其间,1949年在巴尔希列尔(Y.Bar-Hillel,1915—1975)的鼓励和支持下,提出了一套描写语言潜在形态的规则系统。1951年在宾夕法尼亚大学完成了硕士论文《现代希伯来语语素音位学》。1951年后,他到哈佛大学学术协会任职,以正式会员的身份从事语言研究工作。1953年,他在《符号逻辑杂志》(Journal of Symbolic Logic)上发表了《句法分析系统》(System of Syntactic Analysis),此文对美国描写语言学的方法进行了形式化描述。他感到,在结构主义的框架中研究语言,往往会得出错误的结论。
为了完成形式语言理论这一有意义的课题,在海里斯的建议下,乔姆斯基从1953年开始学习哲学、逻辑学和现代数学。这个时期,他受到了古德斯曼(N.Goodsman)的“构造分析法”的影响,也受到了奎恩(W.V.O.Quine)对逻辑学中的经验主义批判的影响,他采用的语言研究方法是严格的、形式化的。同时,他对美国描写语言学的方法越来越不满意,在哈勒(M.Halle)的支持下,乔姆斯基决心同结构主義思想彻底决裂,另起炉灶,走自己的新路。
1954年,乔姆斯基着手撰写《语言理论的逻辑结构》(The Logical Structure of Linguistic Theory)一书。在这部著作中,他初步勾画出生成语法的理论观点和思想方法。1955年,《语言理论的逻辑结构》(Chomsky,1975)书稿完成,乔姆斯基回到宾夕法尼亚大学,并以论文《转换分析》(Transformational analysis)获得了博士学位。
1955年秋,乔姆斯基经哈勒和雅可布逊推荐,到麻省理工学院(MIT)电子学研究室做研究工作,并在现代语言学系任教,给研究生讲授语言学、逻辑学、语言哲学等课程。麻省理工学院电子学研究室在著名学者魏斯奈尔(Jerome Wiesner)的领导下,为多学科的联合研究提供了良好的环境,这样,乔姆斯基就可以专心致志地从事自己的研究工作。
这时,乔姆斯基的形式语言理论的思想已基本成熟,他更加清晰地认识到结构主义的方向是完全错误的,他开始大胆地向结构主义挑战。
1956年,在哈勒的建议下,乔姆斯基把自己在麻省理工学院给本科生讲课的一些笔记,交给了荷兰摩顿(Mouton)公司的《语言学丛书》(Janua Linguarum)的编辑舒纳费尔德(C.V.Schoonefeld)。舒纳费尔德独具慧眼,答应出版这些笔记。经过一番修改之后,由摩顿公司在1957年以《句法结构》(Syntactic Structures)为题出版。此书的出版,得到了美国陆军通讯兵团,美国空军科学研究署、空军研究部、空军开发部和美国海军研究署的资助,还得到了美国国家科学基金会和伊斯特曼·柯达公司的资助。可见美国海陆空三军以及美国国家基金会对此书的重视。
从此,乔姆斯基的语言学说开始在语言学界传播开来,并进一步发展成为众所周知的转换生成语法(transformational generative grammar)。2002年,德国德古意特公司(De Gruyter GmbH&Co.KG)出版了《句法结构》的第二版(Chomsky,2002)。可以说,《句法结构》是自然语言形式分析的奠基性著作,对于现代语言学的发展具有重要的意义。
在撰写《句法结构》前后,乔姆斯基还在1956年至1963年间,发表了《语言描写的三个模型》(Chomsky,1956)、《论语法的一些形式特性》(Chomsky,1959)、《上下文无关语法和后进先出存储器》(Chomsky, 1962)和《语法的形式特性》(Chomsky,1963)等论文。本文也结合这些论文来分析《句法结构》,这样将有助于我们更加深入地理解《句法结构》的内容。
二、形式语言理论
乔姆斯基在《句法结构》中,以语言学家可以理解的方式介绍了他的形式语言理论(formal language theory)和转换语法(transformational grammar)。
(一)语法生成的方法
形式语言理论的研究对象,除了自然语言之外,还包括程序语言和其他人造语言。在形式语言理论中,语言(Language)被看成是一个抽象的数学系统,乔姆斯基把它定义为:按一定规律构成的句子(Sentence)或符号串(String)的有限的或无限的集合,记为L。
每个句子或符号串的长度是有限的,它们由有限数目的符号相互毗连而构成。构成语言的有限个符号的集合,叫做字母表 (alphabet)或词汇 (Vocabulary),记为V;不包含任何符号的符号串,叫做空句子(empty Sentence)或空符号串(empty String),记为ε。
如果V是一个字母表,那么,把由V中的符号构成的全部句子(包括空句子ε)的集合,记为V*,而把V中除了ε之外的一切句子的集合,记为V+。例如,如果V={a,b},则
V*={ε,a,b,aa,ab,ba,bb,aaa,…}
V+={a,b,aa,ab,bd,bb,aaa,…}
但是,某语言的字母表V中的符号相互毗连而成的符号串,并不一定都是该语言中的句子。例如,“the boy hit the ball”在英语中是正确的,叫做“成立句子”;而由同样符号构成的“*the hit the boy hall”在英语中却是不正确的,叫做“不成立句子”。为了区别一种语言中的成立句子和不成立句子,就有必要把这种语言刻画出来,从而说明在这一种语言中,什么样的句子是成立的,什么样的句子是不成立的。
乔姆斯基认为,可以采用三种办法来刻画语言。
第一种,穷尽枚举法,即把语言中的全部成立句子穷尽地枚举出来。
如果语言只包含有限数目的句子,要穷尽地枚举是能办到的;而如果语言中句子数目是无限的,用简单枚举的办法就行不通。
而且,在很多场合,对于语言中某一个长度有限的句子,还可以采用一定的办法将其长度加以扩展。例如,对于英语句子
This is the man.(这是那个男人。)
我们可以将其扩展为:
This is the man that married the girl.(这是那个同姑娘结婚的男人。)
还可以进一步扩展为:
This is the man that married the girl that brought some bread.(這是那个和带来了一些面包的姑娘结婚的男人。)
乔姆斯基认为,可以在句子里加上任意数目的that-从句,每加一个这样的从句就构成了一个新的更长的句子,而这些句子都是成立的。究竟能加多少个that-从句,只与讲话人的记忆力及耐心有关,而与语言本身的结构无关。从这个意义上说,人们能够加上无限数目的that-从句而使句子保持成立。在这样的情况下,用穷尽枚举的办法来刻画语言显然是行不通的。
第二种,语法生成法,即制定有限数目的规则来生成(generate)语言中无限数目的句子。
例如,上面三个句子可以这样统一地加以描述:
设X是一个初始符号,S为句子,R为that-从句,提出重写规则:
X→S
S→S︵R
这里,“→”是重写符号, “︵”是毗连符号,利用这两条规则,可以生成数目无限的带that-从句的句子。
乔姆斯基把这些数目有限的刻画语言的规则,叫做“语法”(grammar),记为G。语法是有限规则的集合,这些规则递归地生成潜在的无限的句子,并排除语言中的不成立句子。语法G所刻画的语言,记为L(G)。需要注意的是,乔姆斯基在这里所说的“语法”,与一般语言学书中所说的“语法”不是一回事,它有着如上所述的特定的含义。
乔姆斯基指出,早在19世纪初,德国杰出的语言学家和人文学者洪堡特(W.V.Humboldt,1767—1835)就观察到“语言是有限手段的无限运用”。但是,由于当时尚未找到能揭示这种观点的本质内容的技术工具和方法,洪堡特的论断还是不成熟的。那么,究竟如何来理解语言是有限手段的无限运用呢?
乔姆斯基认为,“一个人的语言知识是以某种方式体现在人脑这个有限的机体之中的,因此语言知识就是一个由某种规则和原则构成的有限系统。但是一个会说话的人却能讲出并理解他从未听到过的句子以及和我们听到的不十分相似的句子。而且,这种能力是无限的。如果不受时间和注意力的限制,那么由一个人所获得的知识系统规定了特定形式、结构和意义的句子的数目也将是无限的。不难看到这种能力在正常的人类生活中得到自由的运用。我们在日常生活中所使用和理解的句子范围是极大的,无论就其实际情况而言还是为了理论描写上的需要,我们完全有理由认为人们使用和理解的句子范围都是无限的。”(Chomsky,1982)
递归是体现“有限手段的无限运用”的最好办法。乔姆斯基提出的“语法”就恰恰采用了递归的办法。
第三种,自动机识别法,即提出一种装置来检验输入符号串,用这种装置来识别该符号串是不是语言L中的成立句子。如果是成立句子,这个装置就接收它;如果是不成立句子,这个装置就不接收它。乔姆斯基把这样的装置叫做“自动机”(automata),它是语言的“识别程序”(recognizer),记为R。
由此可见,刻画某类语言的有效手段,是语法和“自动机”。语法用于生成此类语言,而“自动机”则用于识别此类语言。
语法和自动机是形式语言理论(formal language theory)的基本内容。如果要想了解乔姆斯基关于语言“生成”的基本概念,必须认真地研究他的形式语言理论中关于语法的论述,否则,我们就很难理解“生成”这一概念的实质。
乔姆斯基从形式上把语法定义为四元组:
G=(VN,VT,S,P)
其中,VN是非终极符号,不能处于生成过程的终点;VT是终极符号,能处于生成过程的终点。
显然,VN与VT构成了V,VN与VT不相交,没有公共元素。我们用∪表示集合的并,用∩表示集合的交,則有
显然,由这个语法生成的语言的符号串,其数目是无限的。
下面,我们来给语法G所生成的语言L(G)下一个形式化的定义。为此,要引入表示V*上的符号串之间关系的符号及。
先对这两个符号的含义作一说明。
如果α→β是P的重写规则,φ1和φ2是V*上的任意符号串,应用重写规则α→β于符号串φ1αφ2,得到符号串φ1βφ2。那么,可写为φ1αφ2φ1βφ2,读为:在语法G中,φ1αφ2直接推导出φ1βφ2。就是说,当应用某个单独的重写规则从第一个符号串得到第二个符号串的时候,表示这两个符号串之间的直接推导关系。
假定α1α2,…,αm是V*上的符号串,并且α1α2,α2α3,…,αm-1αm,那么,这种关系可以写为α1αm,读为:在语法G中,α1推导出αm。由此可见,表示α1和αm这两个符号串之间的推导关系。换句话说,如果应用P中的若干个重写规则由α得到β,那么,对于两个符号串α与β,就有αβ。
这样,由语法G生成的语言L(G)的形式化定义为:
L(G) = (W︱W在中,并且SW)。
这个定义的含义是:对于一切符号串W的集合,W在中,并且有SW,那么,符号串W的集合就是由语法G生成的语言L(G)。
由此可见,一个符号串处于L(G)中要满足两个条件:
条件1:该符号串只包括终极符号;
条件2:该符号串能从初始符号S推导出来。
同一语言可由不同的语法来生成,如果L(G1) =L(G2),则语法G1等价于语法G2。
前面所定义的语法G=(VN,TT,S,P),其重写规则为φ→ψ,并且要求φ≠。
(二)语法生成的类型
以上定义的语法,生成能力过于强大。有鉴于此,乔姆斯基给上述语法加上了程度不同的限制,从而得到了生成能力各不相同的几类语法:
限制1:如果φ→ψ,那么,存在A,φ1,φ2,ω,使得φ=φ1Aφ2,ψ=φ1ωφ2。
限制2:如果φ→ψ,那么,存在A,φ1,φ2,ω,使得φ=φ1Aφ2,ψ=φ1ωφ2,并且A→ω。
限制3:如果φ→ψ,那么,存在A,φ1,φ2,ω,使得φ=φ1Aφ2,ψ=φ1ωφ2,A→ω,并且ω=aQ或ω=a,因而,A→aQ或A→a。
限制1要求语法的重写规则全都具有形式φ1Aφ2→φ1ωφ2,这样的重写规则在上下文φ1→φ2中给出A→ω。显然,在这种情况下,ψ这个符号串的长度(即ψ中的符号数)至少等于或者大于φ这个符号串的长度(即φ中的符号数),如果用|ψ|和|φ|分别表示符号串ψ和φ的长度,则有|ψ|≥|φ|。由于在重写规则φ1Aφ2→φ1ωφ2中,每当A出现于上下文φ1→φ2中的时候,可以用ω来替换A,因此,把加上了限制1的语法叫做上下文有关语法(context-sensitive grammar)或1型语法(type 1 grammar)。
限制2要求语法的重写规则全都具有形式A→ω,这时上下文φ1─φ2是空的,在运用重写规则时不依赖于单个的非终极符号A所出现的上下文环境。因此,把加上了限制2的语法叫做上下文无关语法(context-free grammar)或2型语法(type 2 grammar)。
限制3要求语法的重写规则全都具有形式A→aQ或A→a,其中,A和Q是非终极符号,a是终极符号。这种语法叫做有限状态语法(finite state grammar)或3型语法(type 3 grammar),有时也叫做正则语法(regular grammar)。
没有上述限制的语法,叫做0型语法(type 0 grammar)。
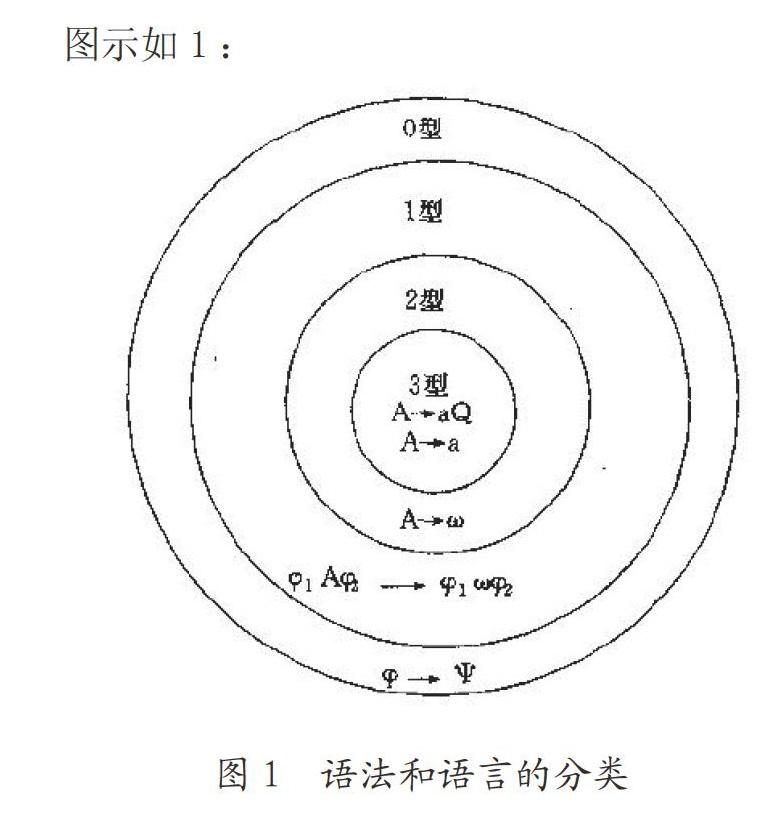
显而易见,每一个有限状态语法都是上下文无关的;每一个上下文无关语法都是上下文有关的;每一个上下文有关语法都是0型的。乔姆斯基把由0型语法生成的语言叫0型语言(type 0 language),把由上下文有关语法、上下文无关语法和有限状态语法生成的语言分别叫做上下文有关语言(context-sensitive language)、上下文无关语言(context-free language)和有限状态语言(finite state language),也可以分别叫做1型语言(type 1 language)、2型语言(type 2 language)和3型语言(type 3 language)。
由于从限制1到限制3的限制条件是逐渐增加的,因此,不论对于语法或对于语言来说,都存在着如下的包含关系①:
1.有限状态语法
有限状态法的重写规则为A→aQ或A→a(A→a只不过是A→aQ中,当Q=时的一种特殊情况)。如果把A和Q看成不同的状态,那么,由重写规则可知,当状态A转入状态Q时,可生成一个终极符号a。这样,便可把有限状态语法想象为一种生成装置,这种装置每次能够生成一个终极符号,而每一个终极符号都与一个特定的状态相联系。
我们改用小写字母q来表示状态,如果这种生成装置原先处于状态qi,那么,生成一个终极符号后,就转到状态qj;在状态qj再生成一个终极符号后,就转到状态qk,如此类推。这种情况可用“状态图”(state diagram)来表示。
如果这种生成装置原先处于某一状态qO,生成一个终极符号a后,转入状态q1,那么,其状态图为图3所示:
如果这种生成装置处于状态qO,生成终极符号a后转入状态ql,在状态q1,或者生成终极符号b后再回到q1,或者生成终极符号c后转入状态q2,在状态q2,或者生成终极符号b再回到状态q2,或者生成终极符号a后转入状态q3,那么,其状态图为图6所示:
第四,有限状态语法只能说明语言中各个符号的排列顺序,而不能说明语言的层次,因此,不能解释语言中的许多歧义现象(ambiguity)。如“o1d men and women”这个短语有两个意思:一个意思是“一些年老的男人和一些女人”(男人都是年老的,而女人未必都是年老的),另一个意思是“一些年老的男人和一些年老的女人”(男人和女人都是年老的)。这种现象不能用有限状态语法来说明其线性排列顺序上有何差异,也不能通过线性排列顺序的差异进行解释。可见,有限状态语法对语言现象的解释力不强。
2.上下文无关语法
为了克服有限状态语法的缺陷,乔姆斯基提出了上下文无关语法。
上下文无关语法的重写规则形式是A→ω。其中,A是单个的非终极符号,ω是异于ε的符号串,即|A|= 1≤|ω|。应该注意的是,“上下文无关”指的是语法中的重写规则形式,而不是指不能利用上下文来限制它所生成的语言。前面提到过的镜象结构语言的语法,其重写规则的左边都是单个的非终极符号S,右边都是异于ε 的符号串①,因而它是上下文无关语法。
上下文无关语法的推导过程,是由“推导树”(derivation tree)来描述的。乔姆斯基又把“推导树”称为语法的“C-标志”(C-marker)。“树”(tree)是图论中的一个概念。树由边(edge)和结(node)组成,它是由边连接着的结组成的有限集合。如果一个边由结1指向结2,那么,就可以说边离开结1而进入结2。如图14所示:
图14 树由边和结组成图
作为图论的树必须满足如下三个条件:第一,树中要有一个没有任何边进入的结,这个结叫做根(root);第二,对于树中的每一个结,都要有一系列的边与根连接着;第三,除根以外,树中的每一个结都只能有一个边进入它,因此,树中没有“圈”(loop)。
如果有一个边离开给定的结m,而进入结n,那么所有的结n的集合就叫做结m的“直接后裔”(direct descendant)。如果有一系列的结n1,n2,……,nk,使得n1=m,nk=n,并且对于每一个i来说,ni+1是ni的直接后裔,那么结n就叫做结m的“后裔”(descendant)。同时规定,一个结是它自身的后裔。
对于树中的每一个结,可以把其直接后裔按顺序从左到右排列起来。
设G=(VN,VT,S,P)是上下文无关语法,如果有某个树满足如下条件,它就是G的推导树:
第一,每一个结有一个标号,这个标号是V中的符号;第二,根的标号是S;第三,如果结n至少有一个异于其本身的后裔,并有标号A,那么,A必定是VN中的符号;第四,如果结n1,n2,……,nk是结n的直接后裔,从左到右排列,其标号分别为A1,A2,……,Ak,那么,A→A1A2……AK,必是P中的重写规则。
从这个推导树可以看出,1、3、4、5、7等结都有直接后裔。结1的标号为S,其直接后裔的标号从左算起为a、A和S,因此S→aAS是重写规则。结3的标号为A,其直接后裔的标号从左算起为S、b、A,因此A→SbA是重写规则。结4和结5的标号为S,它们每一个的直接后裔的标号为a,因此S→a是重写规则。结7的标号为A,其直接后裔的标号从左算起为b和a,因此A→ba也是重写规则。由此可见,刚才画出的语法G的推导树,满足了推导树所要求的各个条件。
在任何树中,总有一些结是没有后裔的,这样的结叫做“叶”(leaf)。如果从左到右读推导树中各个叶的标号,就可以得到一个终极符号串,这个终极符号串叫做推导树的“结果”(result)。可以证明,如果α是上下文无关语法G=(VN,VT,S,P)的结果,则Sα。例如,在上述推导树中,各个叶从左到右的编号为2、9、6、10、11和8,它们的标号分别是a、a、b、b、a、a,则推导树的结果α=aabbaa,因此,Saabbaa。
在实际使用中,常常将推导树的结及其编号去掉,把推导树加以简化。如前面的推导树可简化为图16:
4.0型語法
0型语法的重写规则是φ→ψ,除了要求φ≠之外,没有别的限制。乔姆斯基证明,每一个0型语言都是符号串的递归可枚举集;他还证明,任何一个上下文有关语言同时又是0型语言,而且还存在着不是上下文有关语言的0型语言。因此,上下文有关语言应包含于0型语言之中,它是0型语言的子集合。
但是,由于0型语法的重写规则几乎没有什么限制,用于描写自然语言颇为困难,它的生成能力太强,会生成难以数计的不成立句子。所以,在乔姆斯基的四种类型的语法中最适用于描写自然语言的还是上下文无关语法。
1985年,美国计算语言学家希布尔(S.Shieber)在《上下文无关性质的反证实例》一文中指出,在瑞士德语中存在着词序的交叉对应现象,也就是存在着如图24所示的符号串(Shieber,1985):
尽管自然语言的大部分现象可以使用上下文无关语法来描述,上下文无关语法是生成语法的基础部分。但是,从总体上看来,自然语言还不能算上下文无关的,自然语言的性质似乎介于上下文无关与上下文有关之间。乔姆斯基在《规则与表达》中指出(Chomsky,1980/2005),自然语言可能比上下文有关语言还要复杂,它是乔姆斯基层级上最复杂0型语言,这是一种“递归可枚举语言”(recursive numerable language)。
自然语言的这种性质反映了它的“计算复杂性”(computational complexity)。关于自然语言的计算复杂性的讨论是语言学理论中一个重要而饶有趣味的问题,我们应当关注这个问题。
乔姆斯基的形式语言理论,对于计算机科学有重大意义。乔姆斯基把他的四种类型的语法分别与图灵机、线性有界自动机、后进先出自动机及有限自动机等四种类型的自动机联系起来,并且证明了语法的生成能力和语言自动机的识别能力的等价性的四个重要结果,即:
第一,若一语言L能为图灵机识别,那它就能由0型语法生成,反之亦然。
第二,若一语言L能为线性有界自动机识别,那它就能由1型(上下文有关)语法生成,反之亦然。
第三,若一语言L能为后进先出自动机识别,那它就能由2型(上下文无关)语法生成,反之亦然。
第四,若一语言L能为有限自动机识别,那它就能由3型(有限状态)语法生成,反之亦然。
乔姆斯基的上述结论,提供了关于语言生成过程与语言识别过程的极为精辟的见解,这对计算机的程序语言设计、算法分析、编译技术、图像识别、人工智能等,都是很有用处的,因而在计算机界产生了很大的影响。特别是在计算机科学家们发现算法语言ALGOL60中使用的巴科斯—瑙尔范式(Bacus-Naur normal form),恰好与乔姆斯基的上下文无关语法等价之后,不少学者都投入了上下文无关语法的研究,精益求精,成绩斐然。在语言学界,上下文无关语法的研究也引起了不少学者的注意,国外有些机器翻译研究机构,就是采用上下文无关语法的基本理论,来进行机器翻译系统设计的。
三、转换语法
(一)转换语法的提出
形式语言理论的成就,并没有使乔姆斯基踌躇满志。他是一个语言学家,他的学术兴趣毕竟还是在自然语言的研究方面,而形式语言理论在自然语言的研究中,并不像在计算机科学的研究中那么奏效。于是,乔姆斯基继续探索,试图找出一种适于描写自然语言的语言理论来。
乔姆斯基认为,Ⅲ是语言理论的最起码的要求,而他自己正是采取第Ⅲ种语言理论的。那么,如何进行语法的选择呢?他提出,选择最优语法的标准有两条:第一条,语法的简单性;第二条,语法的解释力。如果一种语法很简单,解释力又很强,那么它就是一种好的语法。
在乔姆斯基的形式语言理论中,语法被理解为语言的生成规则的集合。如果仅从这一意义上来理解语法,那么这种语法也可以看成是一种狭义的语法。按照语法的簡单性和解释力来比较乔姆斯基的四种类型语法,可以看出,在描写自然语言方面,上下文无关语法较为简单,解释力也比较强,因而是一种较好的语法。
然而即使是从简单性和解释力的标准来衡量上下文无关语法,它仍然存在着美中不足之处。
第一,有些歧义的句子,用上下文无关语法的层次分析方法不能加以辨别和解释。如“the shooting of the hunters”的层次分析如图26所示:
然而,如果我们了解到“the shooting of the hunters”是从“they shoot the hunters(他们向猎人开枪)”变换来的,那么就可以肯定,它的意思是“射击猎人”,而不可能是“猎人射击”。
又如“Flying planes can be dangerous”这个句子也是有歧义的:一个意思是“开飞机可能是危险的”,一个意思是“飞着的飞机可能是危险的”。但不论是哪一个意思,其层次结构都是一样的,用上下文无关语法也不能加以解释。然而,如果了解到它是从“Planes which are flying can be dangerous”变换来的,就可以肯定它的意思是“飞着的飞机可能是危险的”。
层次分析反映的是一个句子的推导树的结构,它显示了一个句子的生成过程。因此,层次分析法这一方法,在实质上反映了形式语言理论中“生成”(generation)这一个基本概念,它不过是“生成”这一基本概念在方法上的体现。正如乔姆斯基所指出的,层次分析法无非就是加加标示,用用括弧,把句子切分成前后相续的成分,并且注明这些成分分别属于哪个范畴,然后再把这些成分切分成更小的范畴的成分等……这样可以一直分到最终成分。因此,这样的分析法,显示不出对语义解释极为重要的各种语法关系。
层次分析法的不足之处,说明了不能再继续停留在“生成”这一概念上。为了提高语言理论的解释力,必须从“生成”过渡到“转换”。
第二,上下文无关语法还不够简单。
假使我们用上下文无关语法生成了终极符号串(即句子)。
“The man opened the door.(那人开了那门。)”也可以用“The door was opened by the man.(那门被那人打开了。)”表达同样的意思。
此外,英语中还有像“The man did not open the door.(那人没有开那门。)”“Did the man open the door?(那人开了那门吗?)”“Didnt the man open the door?(那人没有开那门吗?)”“The door was not opened by the man.(那门没被那人打开。)”等等这样一些句子。
如果采用上下文无关语法来生成这些句子,那么势必要对每一个句子都建立一套生成规则。这样一来,语法就显得笨重不堪了。实际上这些句子是彼此相关的,如果我们以“The man opened the door.(那人开了那门。)”为核心句,其他句子都可以由这个核心句通过不同的转换而得到。这样就有可能把语言理论进一步简化。
可见,以语言理论的简单性这一标准来衡量,也有必要从“生成”过渡到“转换”。
于是,乔姆斯基另辟蹊径,提出了“转换语法”(transformational grammar)。这里我们采用“语法”这个术语,是因为“语法”已经不仅仅是指“生成”,而且还有着更为广泛的含义。
乔姆斯基关于转换语法的观点,既受到了法国哲学家笛卡儿(R.Descartes,1596—1650)及17世纪法国波尔·洛瓦雅尔语法学家们的影响,也受到了他的老师海里斯的影响。
法国波尔·洛瓦雅尔教派的语法学家阿尔诺(A.Arnaud)和朗斯诺(C.Lancelot),曾经使用转换的方法来分析句子(安托尼·阿尔诺, 2011)。例如:
“The invisible God has created the visible world.(无形的上帝创造了有形的世界。)”这个句子,是从“God who is invisible has created the world which is visible.”这个句子推出来的,而后面这个句子又可以从下面的核心句推出来:“God has created the world.(上帝创造了世界。)”“God is invisible.(上帝是无形的。)”“The world is visible.(世界是有形的。)”
乔姆斯基对波尔·洛瓦雅尔语法学家们的工作给以很高的评价。
海里斯早就看出了上下文无关语法的局限性,并提出了转换的初步概念。他认为,句子从其外部形式来看,是一个复杂的客体,它是由以某种方式结合起来的、一定数量的所谓“单纯形”(simplex)所组成的。这些单纯形的句子,叫做“核心句”(kernels)。核心句能用上下文无关语法生成或描写。但是,复杂的句子则是应用一系列规则的产物,这一系列的规则称为“转换规则”(transformational rules)。
例如,“John read the good book which was lent to him by Bill.(约翰读了比尔借给他的那本好书。)”这个句子,可以有下列核心句:“Bill lent a book to John.(比尔借了一本书给约翰。)”“The book is good.(这本书很好。)”“John read the book.(约翰读了这本书。)”
运用转换规则,便能由这些核心句生成上面的复杂句。
(二)转换语法的理论
乔姆斯基采用了海里斯的观点,提出了转换语法。而且,青出于蓝而胜于蓝,他走得比海里斯远得多,他对“转换”这一概念提出了严格的形式化的定义:
四、乔姆斯基的局限
乔姆斯基的上述句法理论,在欧美语言学界引起了很大的震动。以耶鲁大学的霍凯特(C.F.Hockett)为代表的“后布龙菲尔德学派”的一些学者,从各个方面来攻击和非难这套新理论。在论战中,同时也在用这种理论来研究英语的过程中,发现它确实还有不少的局限。主要是:
第一,转换语法把一些句子定为核心句,语言中的其他句子均由核心句转换而来。但在语言研究中,哪些句子是核心句,哪些句子不是核心句,很难定出一个确切的标准。乔姆斯基把主动句规定为核心句,但是在英语中,被动句用得相当普遍,许多在汉语中用主动句表达的意思,在英语中却用被动句表达。那么,为什么不能把被动句看成核心句呢?可见,所谓“核心句”的提法是不科学的,在实践中也是行不通的。所以,后来乔姆斯基只好取消了核心句的提法,因而也就放弃了强制转换和随意转换的区别的理论。
第二,不论是形式语言理论还是转换语法,对于语义都研究得很不够,它们都不能反映语义之间的搭配关系。例如,根据形式语言理论,提出一个适当的语法,便可生成“the man saw the ball”这样的句子,这个句子的各个成分在语义上可以很自然地搭配起来。但是,用同样的语法,也可生成“*the ball saw the man”,这个句子并不违背上下文无关语法的规则,可是其中的各个成分在语义上搭配不起来,因为saw这个动词要求前面的名词一定是“有生命的”。在上下文无关语法中却不能反映这种语义上的搭配关系,转换语法当然也说明不了这种语义上的搭配关系。
上面我们对于乔姆斯基的形式语言理论到转换语法的发展历程做了概括的说明,可以看出,60年前出版的乔姆斯基的《句法结构》一书,是自然语言形式分析的奠基力作,我们应当认真学习和研究本書中提出的理论和方法,以推动我们语言学的现代化进程。
参考文献:
[1]N.Chomsky.Three models for the description of language[J].The Journal of Symbolic Logic,1956,(3).
[2]N.Chomsky.Syntactic Structures[M].The Hague: Mouton,1957.
[3]N.Chomsky.On certain formal properties of grammars [J].Information and Control,1953,(2).
[4]N. Chomsky.Context-free grammar and pushdown storage, Quart.Prog.Dept.No.65,MIT Res.Lab.Elect,1962.
[5]N. Chomsky.Formal properties of grammars[A].Handbook of Math.Psych[C].NewYork:Wiley,1963.
[6]N. Chomsky.The Logical Structure of Linguistic Theory (LSLT)[M].NewYork:Plenum,1975.
[7]N.Chomsky.Syntactic Structuresc Second Edition[M].Berlin:Walter de Gruyter,2002.
[8]N.Chomsky.Rules and Representations,Manhatton:Columbia University Press,1980/2005.
[9]S.Shieber.Evidence Against the Context-Freeness of Natural Language[J].Linguistic and Philosophy,1985,(8).
[10][美]乔姆斯基.乔姆斯基序[A].赵辛而译.黑龙江大学外语学刊编辑部编.乔姆斯基语言理论介绍[C].哈尔滨:黑龙江大学,1982.
[11][法]安托尼·阿尔诺,克洛德·朗斯洛.普遍唯理语法[M].张学斌,柳利译,姚小平校.北京:商务印书馆,2011.
[12]冯志伟.形式语言理论[J].计算机科学,1979,(1).
[13]冯志伟.从形式语言理论到生成转换语法[A].语言研究论丛(第二辑)[C].天津:天津人民出版社,1982.
[14]冯志伟.生成语法的公理化方法[A].哈尔滨生成语法讨论会论文集[C].哈尔滨:黑龙江大学,1983.
[15]冯志伟.自然语言的计算复杂性[J].外语教学与研究,2015,(5).
