超大型矿砂船干模态分析

李 华, 王炫凯

(上海船舶运输科学研究所 航运技术与安全国家重点实验室,上海 200135)

0 引 言

船舶在波浪的作用下可能会产生很大的动力响应，在设计和使用过程中必须考虑其水弹性。已往在研究船舶在规则波中航行过程中的运动和受力情况时，通常假定船舶是刚性体，忽略其弹性变形，在采用“切片理论”求得船舶在波浪中的运动和受力情况之后，根据材料力学静平衡法得到船体各剖面上的波浪诱导弯矩和切力。实际上船舶是弹性物体，在波浪中航行过程中不仅会产生刚体六自由度运动，而且会产生振动和弹性变形，研究船舶在波浪作用下的振动,即是研究船舶水弹性，而船体干模态分析是船舶水弹性分析的基础[1]。

目前常用的船体干模态分析方法主要有迁移矩阵法和三维有限元法,其中:迁移矩阵法具有输入参数简单和计算效率高的优点，但难以考虑弯扭耦合振动，且无法获得局部振动振型;三维有限元法不仅能用来计算弯扭耦合振动，而且能获得船体局部板架的振型，缺点是需建立三维有限元模型，工作量较大。

本文采用三维有限元法进行干模态分析，对干模态分析的原理进行简要介绍，并以一艘超大型矿砂船为例进行计算分析。

1 三维有限元法干模态分析

超大型矿砂船由于船体的刚度较弱，局部板架振动可能会与船体总振动发生耦合，三维有限元法可用来分析这种耦合情况[2-4]，下面对该方法的原理进行简要介绍。

1.1 自由振动方程

多自由度无阻尼体系自由振动方程为

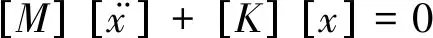
(1)

设x=φsin(ωt+α)，将其代入式(1)可得

([K]-ω2[M])[φ]=0

(2)

若式(2)有非零解，则其系数行列式为零，有

|[K]-ω2[M]|=0

(3)

上述问题归结为求式(2)的广义特征值。展开式(2)中的系数行列式，可得到该系统的n个自由振动圆频率ω1,ω2,ω3,…,ωn;将自由振动圆频率按从小到大的顺序排列成向量，称作圆频率向量，其中最小的圆频率称作第一圆频率。

对于ωi(i=1,2,3,…,n)，相应的主振型向量为

{φ}={φ}i,i=1,2,3,…,n

(4)

式(4)中:n为离散后船体结构的自由度数。主振型之间具有正交性，对于具有n个自由度的系统，可将其n个主振型向量组成方程，称之为主振型矩阵,即

(5)

1.2 兰索斯方法

Nastran程序含有7种特征值计算方法,其中兰索斯方法既能克服其他方法的局限性，又具有其他方法的优点。兰索斯方法采用Sturm序列，检查小于试验特征值的特征值数目，在指定的范围内求解小于试验特征值的所有特征，确保找到所有模态，不仅计算效率高，而且不会丢根，在求解中型或大型特征值问题上具有突出优势[5]，因此本文采用该方法进行正则模态计算。

2 实船分析

2.1 有限元模型

以一艘40万吨级超大型矿砂船为例，采用三维有限元法进行干模态分析，并对结果进行对比。船型主要参数为:规范船长353 m;型宽65 m;满载吃水22.998 m;压载吃水13.462 m;满载排水量45.1万t;压载排水量25.3万t。

在采用三维有限元法计算船体干模态时，应准确模拟船体质量的分布情况，压载水的质量和货物的质量都需考虑到。在干模态分析中，常用的装载质量加载方法有：

1) 精调密度法，即改变分段的材料密度模拟装载质量；

2) 集中质量法，即在舱壁各节点建立集中质量单元，各集中质量单元的质量为该段装载质量与舱壁上节点总数的比值。

上述2种方法都不能合理地模拟出装载货物的重心，本文采用多点约束(Multi-Point Constraint,MPC)建立RBE3柔性单元，将主节点设在装载货物的重心处，从节点为舱壁上各节点，这样既能模拟出装载货物的质量，又能保证有限元模型各段的重心位置与实际装载时船舶各分段的重心位置一致。图1为干模态分析有限元模型。

图1 干模态分析有限元模型

2.2 计算结果分析

1) 压载情况下的部分振动振型见图2，满载和压载情况下的固有频率计算结果见表1。从图2a～图2c中可看出，前几阶垂向振动几乎没有与水平振动和扭转振动发生耦合;从图2e中可看出,三阶水平振动虽然整体上表现为水平振动，但有比较明显的扭转振动，因此应是水平振动与扭转振动的耦合。由表1可知,固有频率由低到高分别为：二阶垂向振动、一阶扭转振动、三阶垂向振动、二阶扭转振动、二阶水平振动、四阶垂向振动、三阶水平振动。

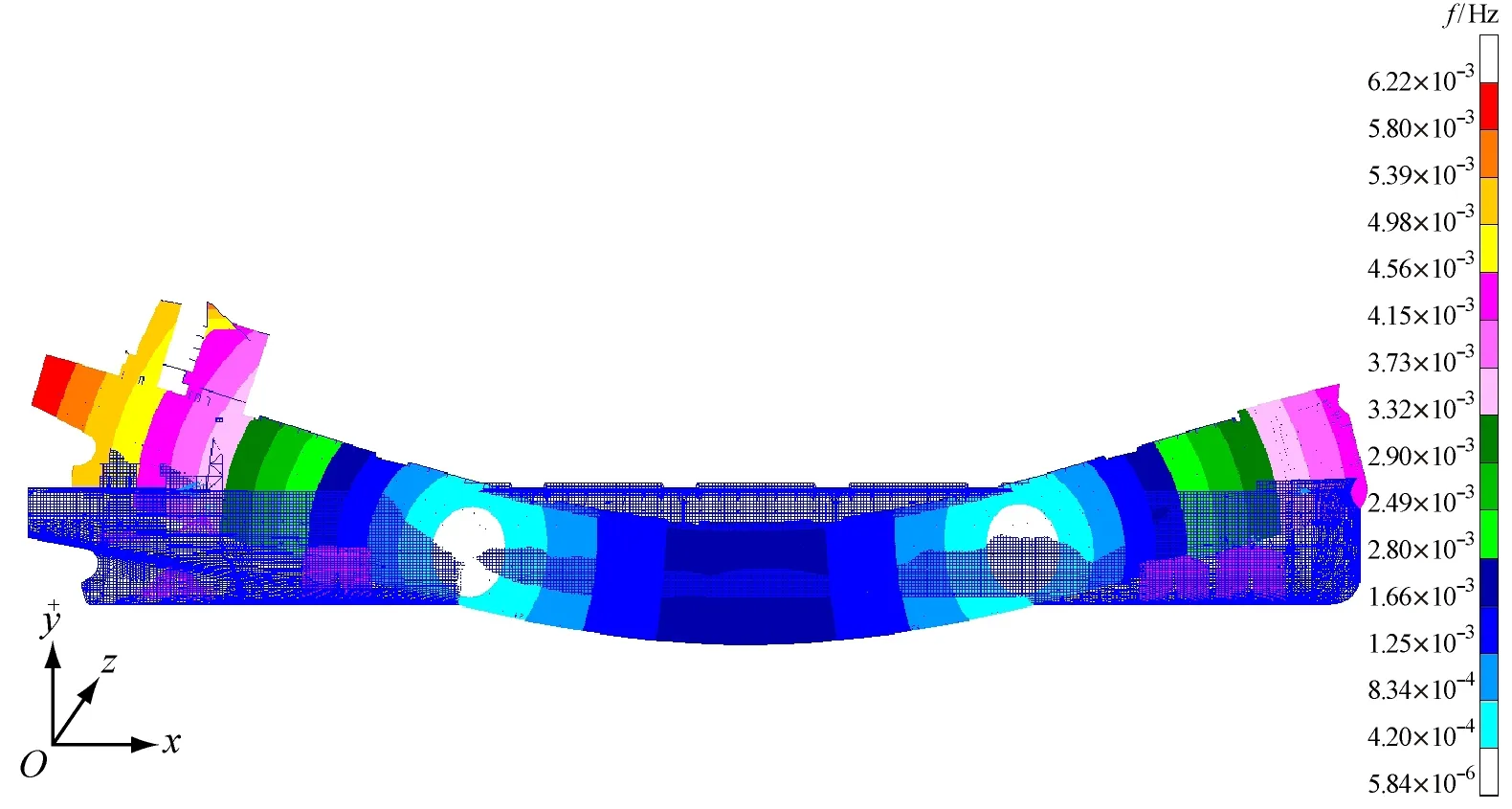
a) 二阶垂向振动

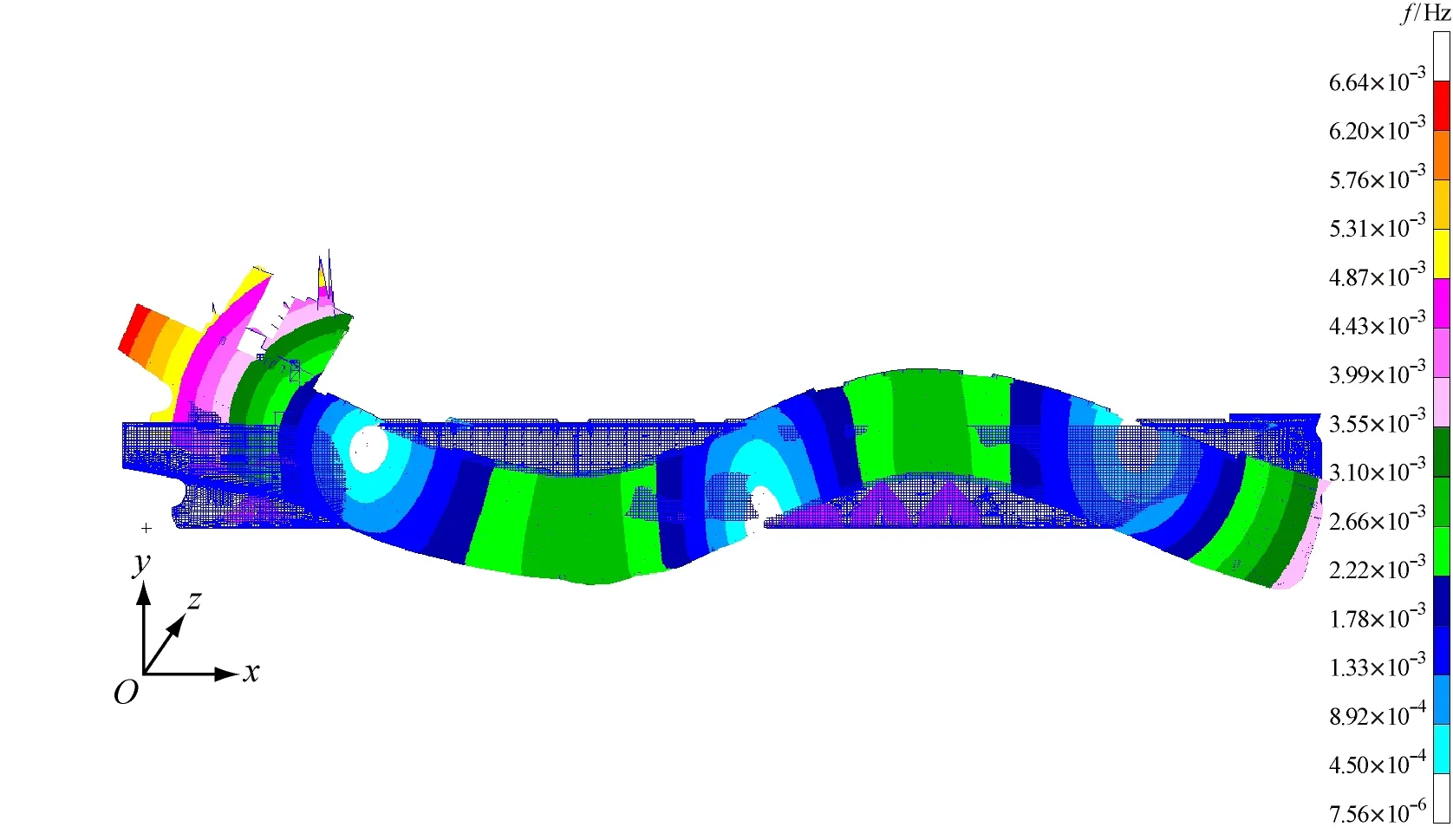
b) 三阶垂向振动

c) 四阶垂向振动

d) 二阶水平振动

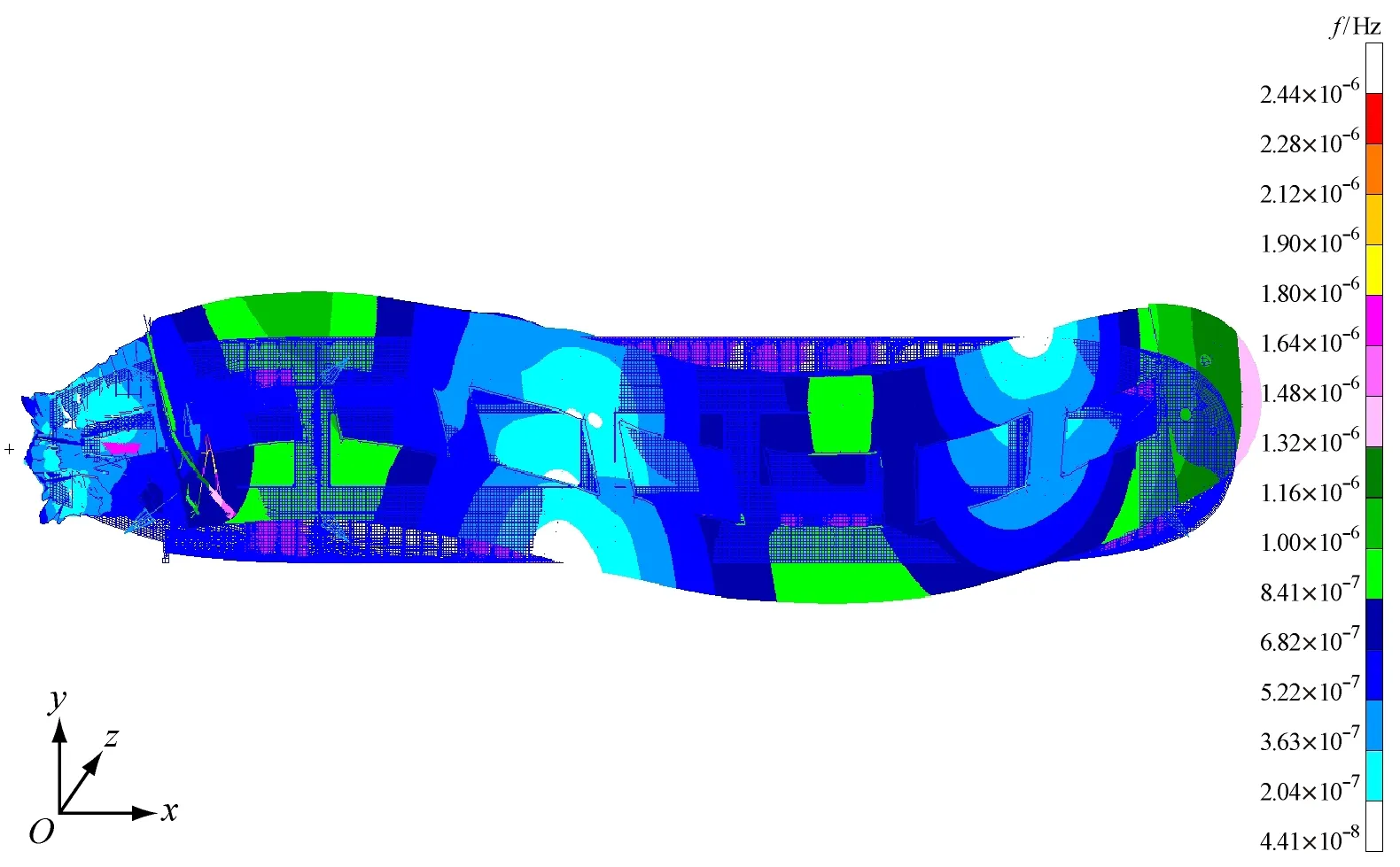
e) 三阶水平振动(俯视图)

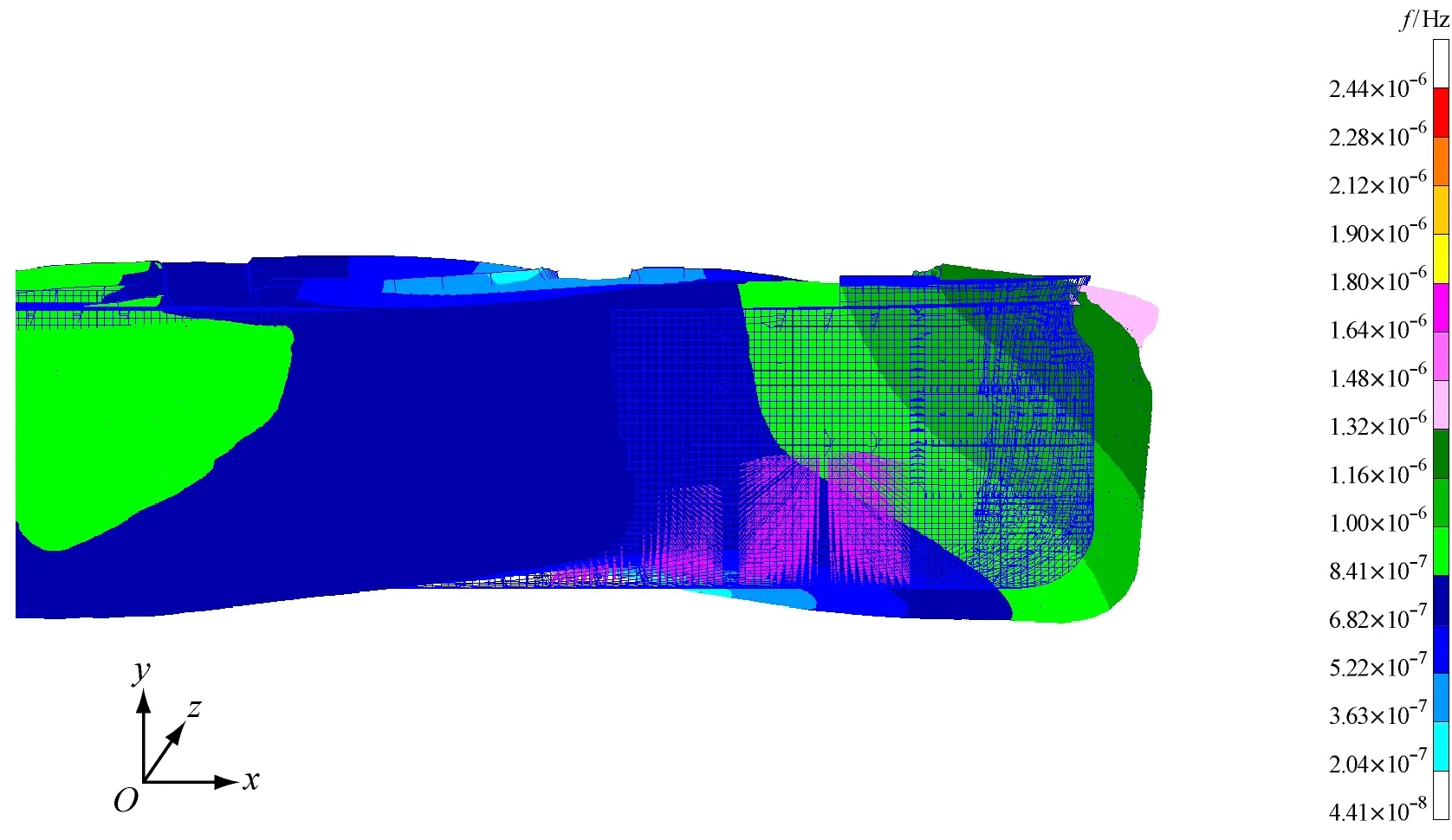
f) 三阶水平振动(侧视图)

g) 一阶扭转振动

2) 横向舱壁振动振型见图3。从图3b～图3d中可看出:对于船体三阶垂向总振动和二阶水平总振动，横舱壁出现一定的局部振动;对于船体四阶垂向总振动和三阶水平总振动，横舱壁表现出明显的局部振动。分析其原因，对于四阶垂向振动和三阶水平总振动，船体振动频率较高，易发生局部板架振动。从图3c和图3e中可看出，在远离振动节点的区域，局部振动更为明显，这是因为压载水的质量较大，在远离振动节点的位置上其惯性力较大，对局部振动的影响也较大。

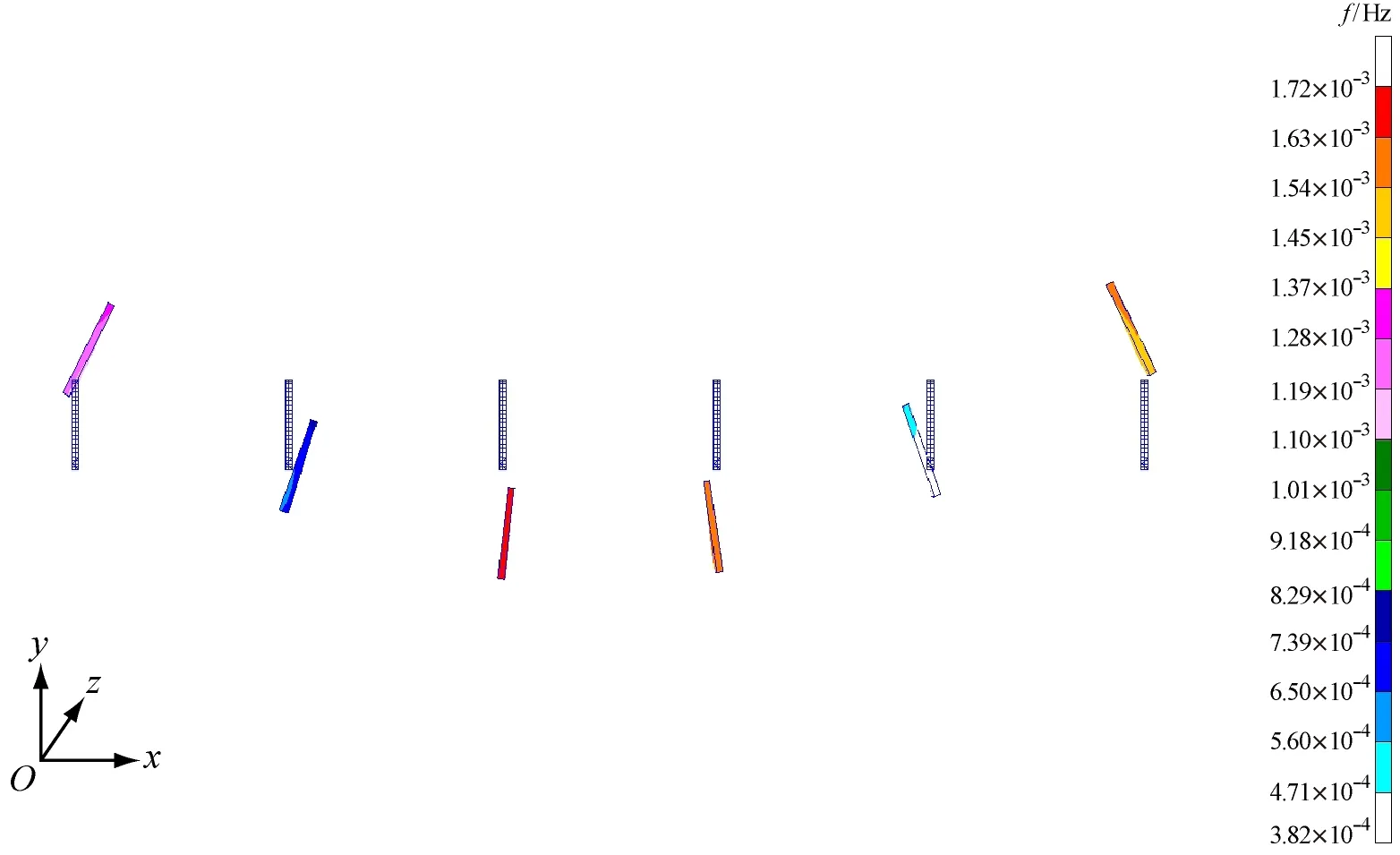
a) 二阶垂向振动

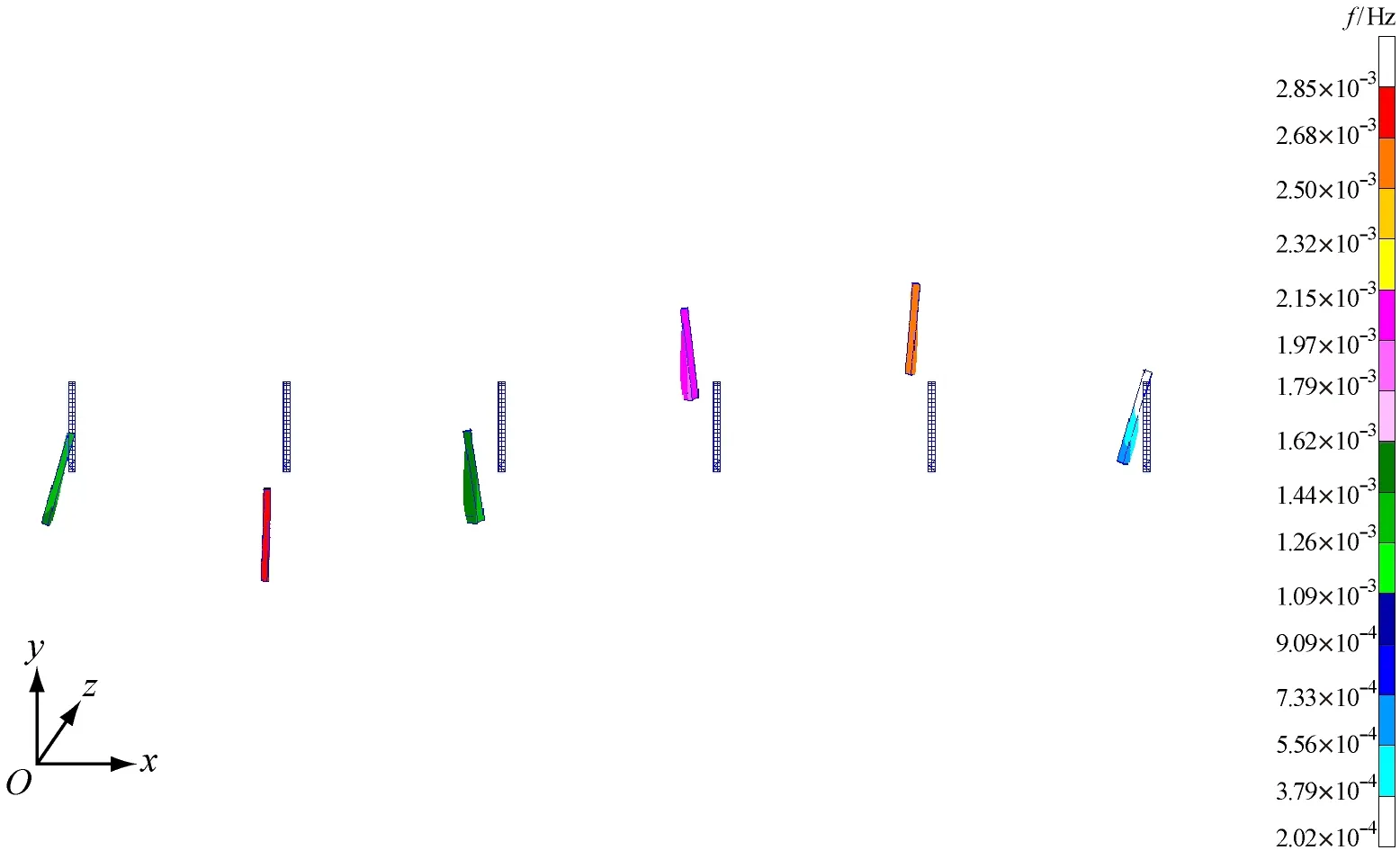
b) 三阶垂向振动

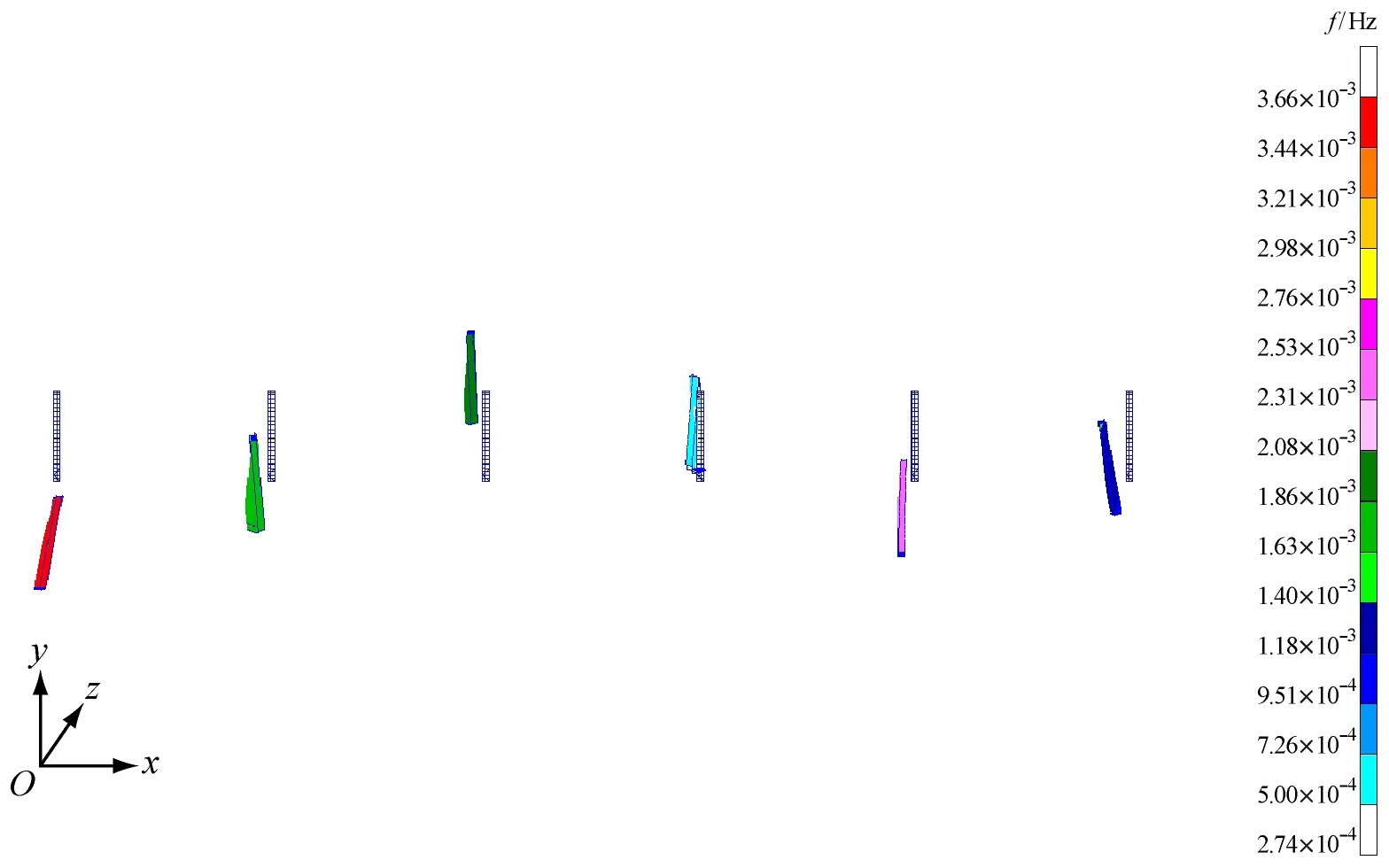
c) 四阶垂向振动

d) 二阶水平振动

e) 三阶水平振动

3) 内底板振动振型见图4。从图4中可看出，内底板的弯曲振动与船体总振动的一致性良好，需注意内底板是水平振动时有较为明显的扭曲现象。

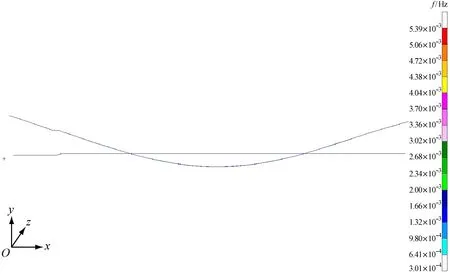
a) 二阶垂向振动

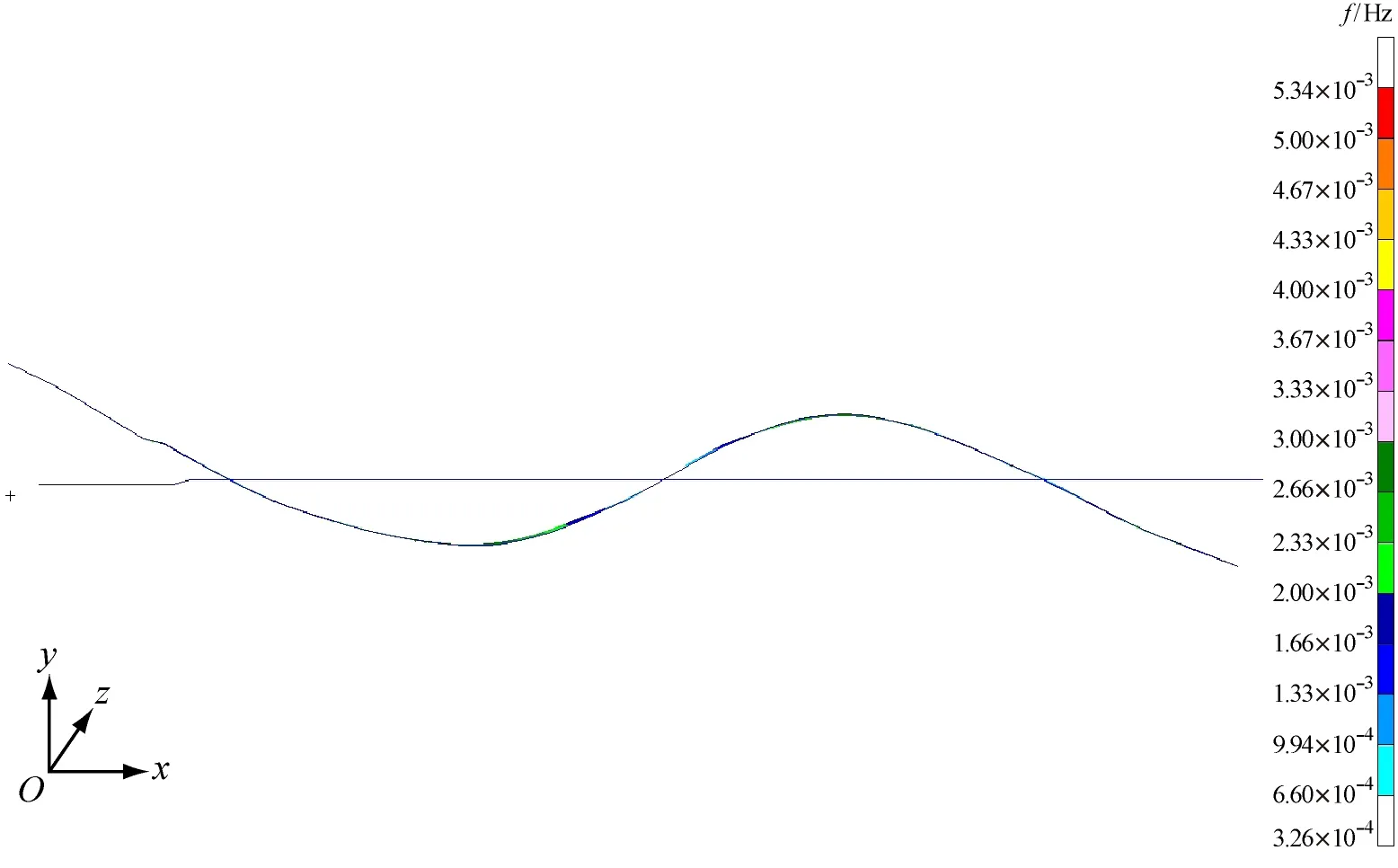
b) 三阶垂向振动

c) 三阶垂向振动

d) 一阶扭转振动

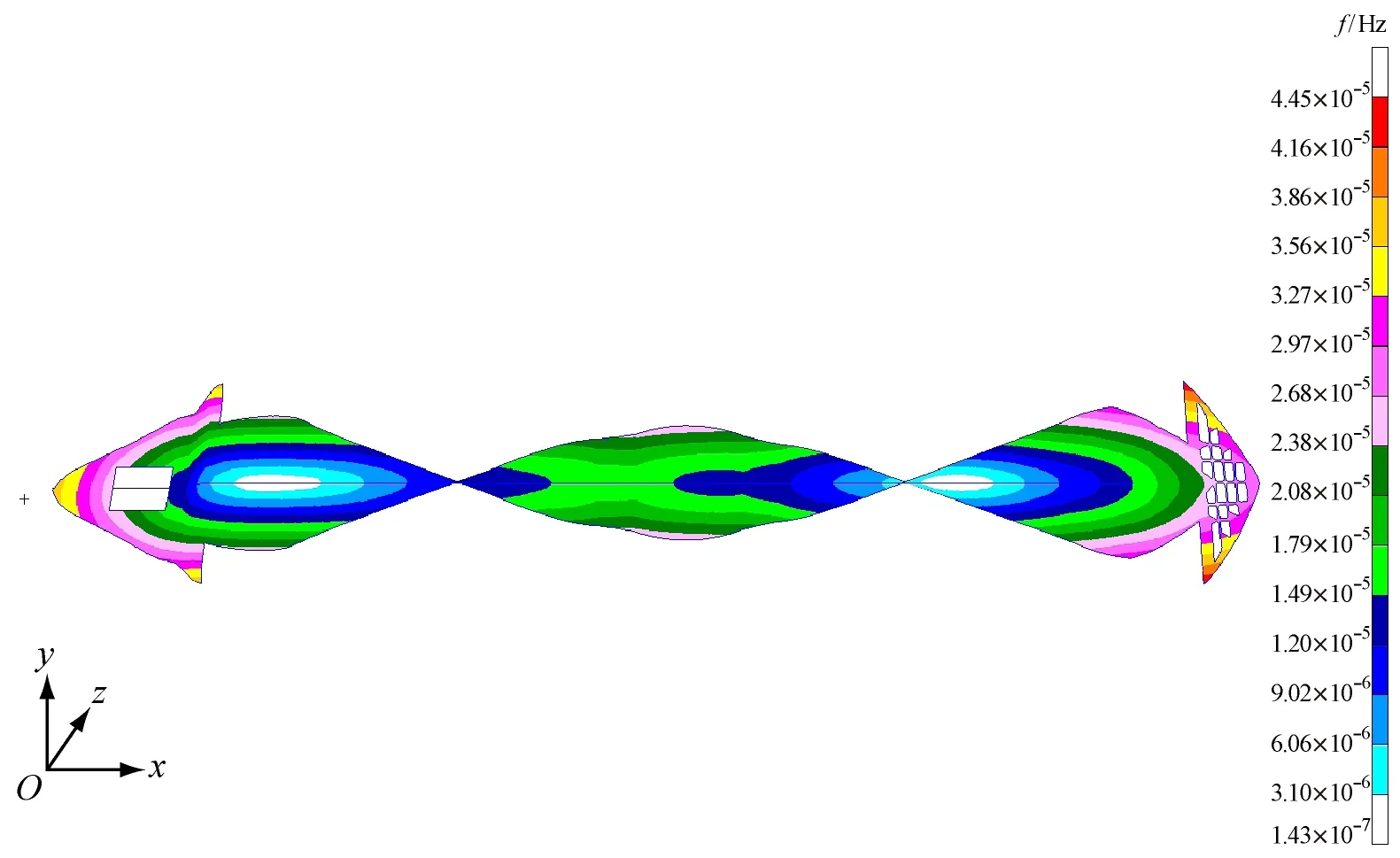
e) 二阶扭转振动

f) 二阶水平振动

g) 二阶水平扭转振动

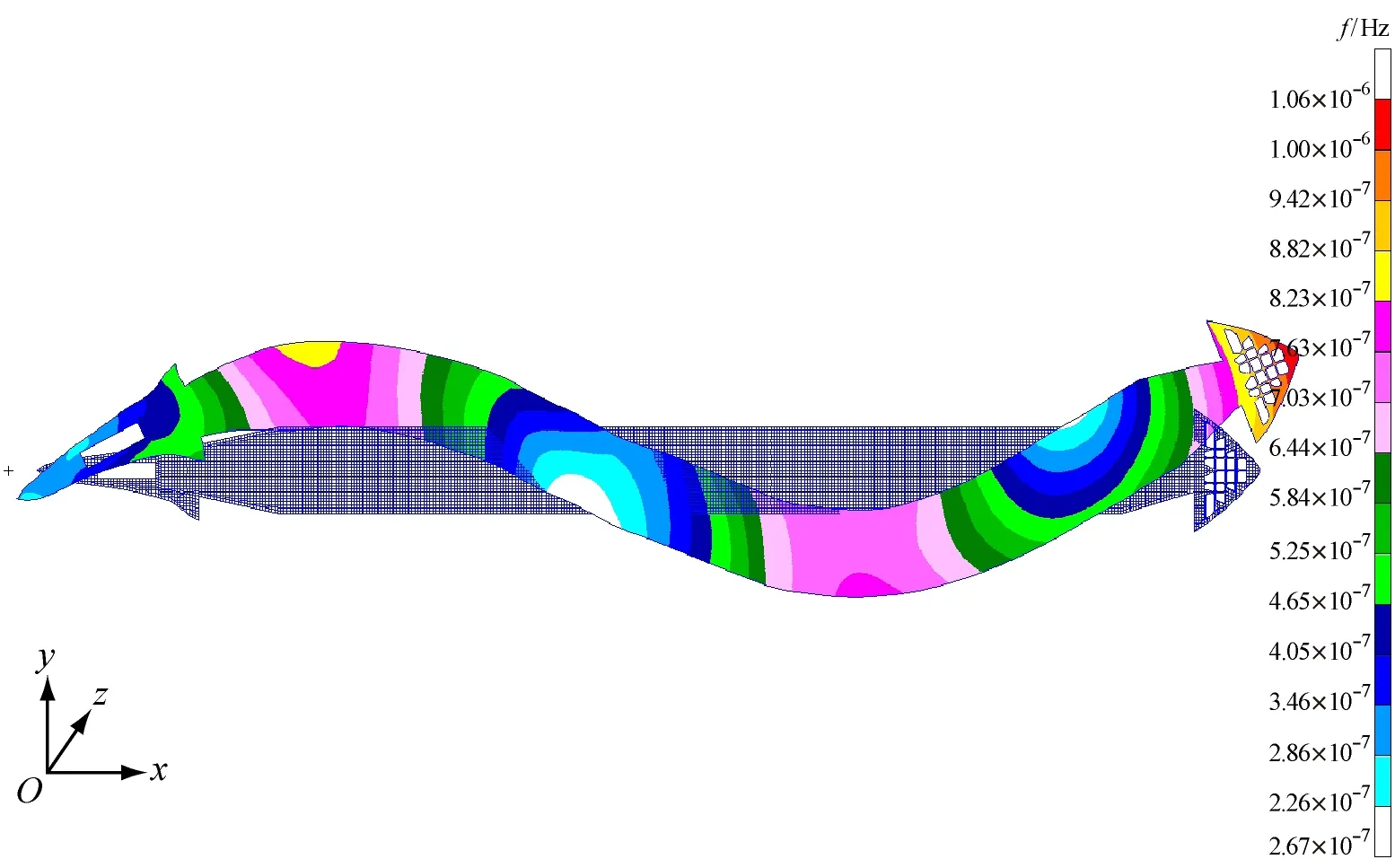
h) 三阶水平振动(侧视图)

i) 三阶水平振动(俯视图)

3 结 语

通过采用三维有限元软件对超大型矿砂船进行干模态分析可知，前几阶的垂向总振动几乎没有发生耦合，但三阶水平总振动发生了较为明显的扭转耦合。由此可知，随着振动频率的增大，耦合现象更容易出现。此外,通过对内底板振动和横向舱壁振动进行分析可知，二者的振动和总振动都具有较好的一致性，但随着振动模态阶数的增加和振动频率的增大，局部振动越来越明显。