六辊薄壁管材矫直机参数设计与仿真分析

杨会林 黄开旺 周传香

(东北大学机械工程与自动化学院 辽宁沈阳110819)

1 前言

六斜辊矫直机在国内矫直厚壁管材方面应用广泛[1]。其中，六个辊子分上下各3个且成对排列。其辊型都是双曲线辊型，但由于分布不同，主要起到的矫直作用也不同。第一对辊子主要起到咬入管材和圆整管材端面的作用，管材在经过第一对辊子时的弹塑性弯曲变形不是很大。当管材经过第二对辊子时，管材的反弯量会增大[2]。管材将发生较大变形，但管材的变形并不是连续的。也就是说会出现矫直盲区，即存在不能被矫直部分。这也是一般六斜辊矫直机的缺点，不能使被矫圆材实现全长矫直。常见的六斜辊矫直机能够相对均匀矫直厚壁管材，但不能用来矫直薄壁管材。

将以原有的六斜辊矫直机为基础进行了辊型的改进，将第二对的双曲线辊型设计为凹凸辊[3]，实现管材的全长矫直，并针对薄壁管特性设计相应的辊型参数。同时通过在压下系统中安装伺服机构可以实现自动补偿机架变形，保证机架能稳定工作，从而使被矫直的薄壁管材具有较高的矫直精度。

2 原理与参数设计

2.1 斜辊矫直原理[4]

2.1.1压扁矫直原理

斜辊矫直机在矫直管材时，管材同时受到反复的纵向弯曲和横断面压扁的综合作用，同时在矫直辊的带动下薄壁管材边旋转边前进。管材的旋转可以使薄壁管材同一个横断面处处得到压扁，起到圆整横断面的作用。不仅可以获得较好的矫直效果，还能对管材起到圆整效果。1处的管材外表面受拉应力，内表面受压应力。区域2处发生塑性变形，外表面受到压应力，内表面受到拉应力。区域3处同区域1处。

图1 管材压扁矫直时的受力状态和压扁力图

由图看出，管材处于矫直辊的辊腰处，并且辊子与辊子之间的距离即辊缝小于管材的外径。由于管材在矫直过程中不停的旋转，管材每一个圆断面上的各个方向都会压扁管材，使管材发生弹塑性变形。从而，起到圆整椭圆端面的作用。

2.1.2反弯矫直原理

多斜辊矫直机中，几对辊子与管材共同构成几个弹塑性弯曲矫直区，使管材每个断面都能被多次反弯，在一定程度上起到矫直的目的。管材在辊子的作用下会旋转，又使管材在不同方向上得到反弯，也就可以改变各个方向上的弯曲曲率，从而改变弯曲半径。被矫直工件每旋转一周就可以反弯两次，矫直辊的个数不需太多就可以达到一定的矫直效果。一般矫直辊构成l～3个弹塑性弯曲单元即可达到想要的矫直精度。

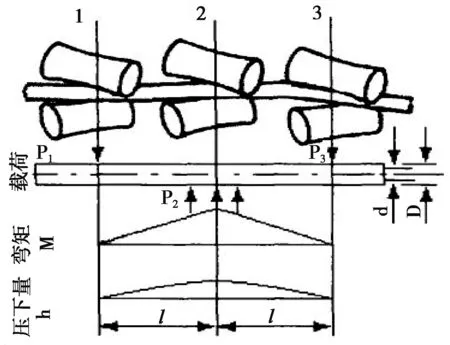
图2 管材弯曲矫直时的弯曲力矩与压弯量图

2.1.3辊系的选取

辊型采用双曲线形式，一方面可以保证矫直辊与管材成线性接触，保证矫直质量。另一方面，利用双曲线形的辊子来约束管材，使其在矫直加工过程中正常旋转前进并且不会偏离生产线。

辊系的安排对矫直精度有很重要的关系，需根据矫直材料的特性来安排辊系的布置，常见的辊系见图3。

图3 斜辊矫直机的典型辊系图a-辊形凹凸扁化； b-椭圆变形； c-管材矫直专用辊系；d-全部驱动辊; e-辊子后加l辊； f-7辊薄壁矫直机；g-9辊高速矫直机

2.2 薄壁管材矫直机辊型设计

2.2.1辊子与管材的关系

下图4显示辊子与管材关系。

图4 辊子与管材的关系图

可得几个速度关系：

矫直辊转动的圆周速度：

(1)

管材前进速度，即矫直速度：

v3=v0sinα

(2)

管材转动的圆周速度，即：

vn=v0cosα

(3)

矫直辊转动速度：

(4)

管材转动速度：

(5)

式中：D0-辊子与管材接触处辊子直径，mm；

n0-辊子的转速，rad/min；

α-辊子倾角，度；

d-管材直径，mm。

根据生产要求，设置矫直辊的转速为2.8rad/min，管材的转速为3.6rad/min，管材的前进速度为40m/min。

2.2.2辊子倾角α的选取

矫直辊与管材之间的夹角，对矫直质量和矫直速度都会有很大的影响。当倾角过小时，矫直速度小，能耗就大。当倾角过大时，管材和辊子的接触线短，管材在被矫直过程中容易发生应力集中，影响矫直质量，甚至出现废品。管材旋转一周前进导程为[5]：

t=πDtanα

(6)

管材的弯曲次数为：

i=lp/t

(7)

式中：D—管材外径，mm;

α—为辊子与管材之间倾角，度；

lp—为弹塑性变形区长度，mm。

从矫直次数方面考虑，若倾角过大，前进导程就大。从而矫直次数减少，使管材的弹塑性变形区面积减小，影响矫直质量。一般矫直机的倾斜角范围为25°—35°，本文选取的矫直辊的倾斜角为α=30°。

2.2.3矫直辊辊腰半径Rg的选取

矫直机的矫直速度为：

v=vgsinα=(2πRgngsinα)

(8)

式中：Rg-辊腰半径，mm ；

ng-为辊子转速，rad/min；

α-辊子倾角，度。

考虑到矫直速度，管材所受的约束力，加工制造成本等因素，基于以上原因，矫直辊的辊腰半径Rg要满足以下要求：

Rg≥(2～3)R

(9)

其中，R—管材外径，mm。

据本文所矫直的管材直径范围φ12～φ35mm，求得Rg=(2～3)R=(2～3)*17.5=35～52.5mm，Rg取为50mm。

2.2.4辊子长度Lg的选取

参照统计数据，采用下式来确定辊子长度：

t≥πDtanα

(10)

Lg=(2～3)t

(11)

式中：D-管材外径，为35mm；

t-为管材的螺旋导程，mm；

Lg-为辊子有效长度，mm。

经计算求得辊子有效长度127～354mm通过经验分析和设计要求，辊子有效长度取200mm。

2.2.5辊距p的选取

辊距的设计对矫直的结构，强度，尺寸都会有很重要的影响。而且，辊距的大小也会对矫直力有影响。辊距越大，矫直力越小，机架的受力就越好。

辊系中各对辊子间的距离可通过下式计算：

p=(2～2.5)Lg

(12)

为考虑设备占地面积，设计的矫直机的整体尺寸不需太大，辊距p取400mm。

2.3 管材的弯曲变形与弯矩分析

判定矫直效果的标准是与管材的塑性变形面积有关，当塑性变形的面积占环形弹塑性变形面积的75%以上时就可达到很好的矫直效果。管材的弯矩比[6]为：

(13)

式中：r-管材内半径，mm；

Rt-弹性核心半径，mm；

ζ1-弹区比，ζ1=Rt/R，无量纲；

α-管材内外半径比，α=r/R，无量纲。

图5 管材的弯矩比和弹区比曲线图

2.4 矫直力的计算

传统的六辊矫直机六个辊子的辊型全是双曲线形，而新六辊系统中间一对辊子设计为一凸一凹的形式。主要是考虑到凹凸辊可以实现管材的全长矫直的优点，然后进行了相应的改进设计。下面通过分析获得了新辊系弯矩和矫直力，见图6。并根据弯矩作用模型，进行的相应情况下3对辊子矫直力的计算。

图6 新222辊系矫直弯矩模型图

矫直力理论计算：

1)钢管内外径比α=r/R=0.77

其中R和r分别为钢管的外半径、内半径，R=17.5mm，r=13.5mm。

2)钢管弹性极限弯矩Mt为：

(14)

式中，σt管材的弹性极限，σt=σs=350MPa。

3)钢管的弹区比ζ=a-0.1=0.67

(16)

得Mmax=1701348N

5)按图8计算矫直力为，凹凸辊辊端弯矩M2由出入口的辊组来实现，力F3为两侧辊组的作用力，力臂为(ρ-Lg)/2。对于单向反弯辊形，在F3处增加一个压紧力F3Y：

式中：t-中间凹凸辊导程，t=Sd=Lg/4=50mm(Sd为中间凹凸辊精矫区，mm) ；

δ-管材壁厚，δ为4mm；

R-管材外径，R为17.5mm。

故F3求得：

(18)

最大弯矩出现在凹凸辊处，而且此处为2个等曲率反弯矩，所以最大矫直力出现在凹凸辊辊腰处为：

(19)

求得F∑=57988N。

轴承受力总和为：

(20)

其中，θ—轴承推角，θ=35°。

求得轴受力承总和即棍面法向受力总和F=24380 N。

2.5 压下系统

在以往矫直机设计中，矫直辊的压下行程和压下量都是人工调整，这就大大降低了工作效率。压下系统中增加了伺服驱动，可以自动补偿机架工作过程中的变形量。从而保证机架工作中的稳定性，实现高精度的要求。

压下过程可电动或手动控制实现。电机或手轮带动蜗轮减速机传动滚珠丝杆实现矫直辊的上下移动，压下采用伺服电机控制，可根据预设参数自动调整压下量，同时现场有位移量的指示表盘(指示精度0.1mm)及相关位移量参数的传感机构，在板式工控机显示压下位移量(显示精度0.01mm)，并可记忆。压下行程为100mm。每个上辊压下过程均为电动或手动单独调整，其压下过程是在非矫直

图7 压下系统图1-压下轴承座；2-压下丝杠；3-压下螺母；4-滑动套；5-矫直辊座；6-矫直辊

3 管材矫直过程仿真分析

验证被矫直管材能否达到想要的矫直精度,利用有限元分析软件模拟实际工作环境对管材矫直过程进行了动态仿真分析。本次仿真分析采用ANSYS/ Explicit STR显示动力学模块进行分析。

3.1 建立模型

在SolidWorks中建立矫直辊与管材的简化模型，导入ANSYS Explicit STR显示动力学模块。将三维模型导入ANSYS/Workbench中对管材的变形进行仿真分析。矫直过程简化模型，见图8。

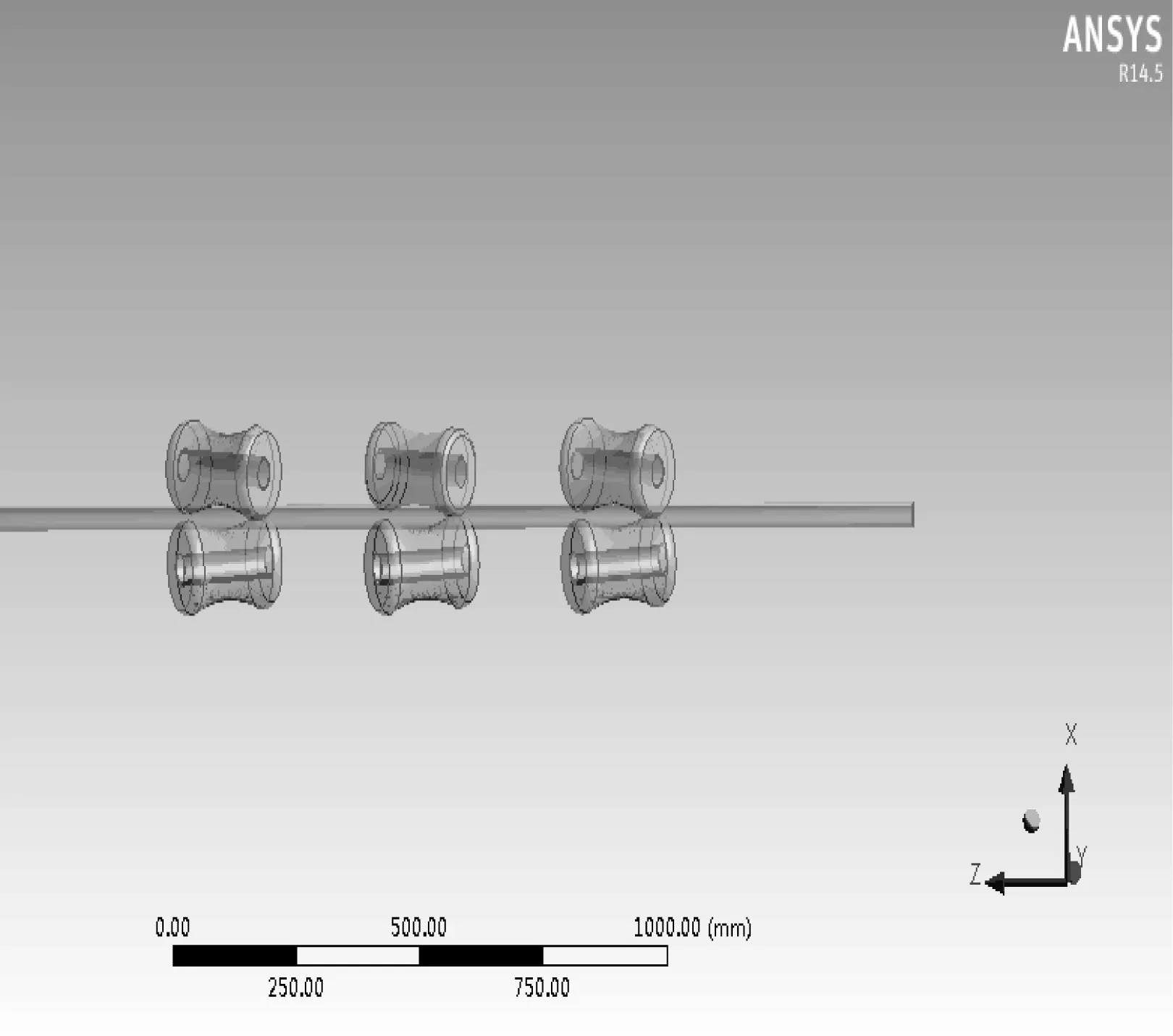
图8 矫直过程简化图

3.2 材料属性的定义

本文要矫直的薄壁管材属于不锈钢或合金管材，其材料特性相当于06Cr19Ni10的属性。管材的基本规格参数为：外径 为35mm，壁厚 为4mm，取管材长度为1000mm。该薄壁管材的材料属性，见表1。矫直辊的材质Cr12MoV,辊面硬度为 HRC58-62，其屈服强度为1370MPa，抗拉强度为1620MPa。

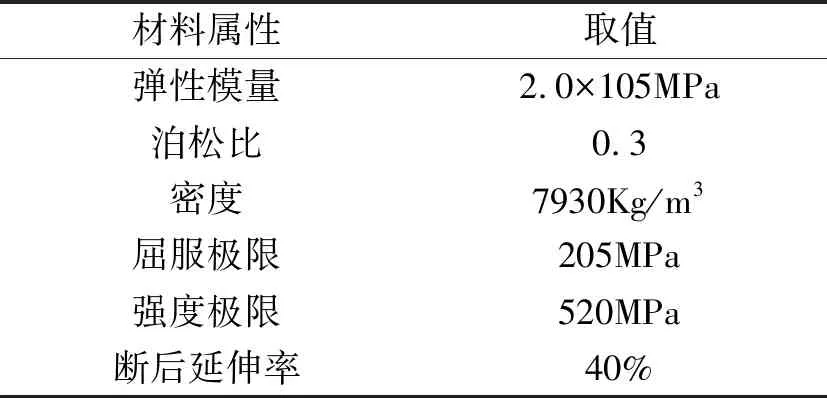
表1 钛合金管材的材料属性

3.3 网格划分

因矫直辊变形量小，为加快仿真速度，将矫直辊设为刚性体，将薄壁管设为变形体。采用自动网格划分。划分完网格后节点数为2512，单元数为11799。其网格划分情况，见图9。

3.4 其它定义

指接触的处理，载荷、边界条件和约束。通过压下系统调整辊子的压下行程和自转速度，管材在辊子的摩擦作用下一边旋转一边前进。同时，辊子给管材施加矫直力时管材被矫直。这里取动摩擦系数0.2，静摩擦系数0.3。6个矫直辊的转速都相同，都有驱动作用。管材矫直速度设为40m/min，转速设为3.6rad/min。

图9 矫直辊和管材网格图

3.5 求解

考虑到仿真存在不收敛现象。分析时间步长取0.0001s。

3.5.1管材矫直稳定状态分析

当矫直过程达到一个稳定状态时，对薄壁管材的变形进行分析，同样时间步长取0.0001s，通过分析最后获得矫直过程中薄壁管材的变形云图，见图10。

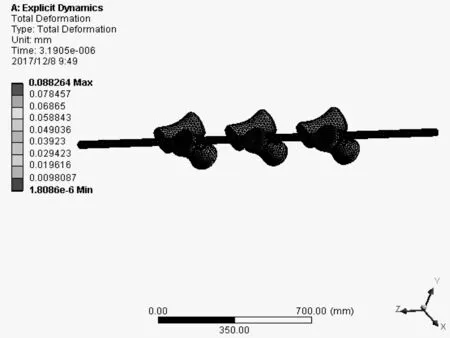
图10 薄壁管材变形云图

通过对矫直辊矫直薄壁管材的仿真变形仿真分析，可以看出随分析时间的变化薄壁管材的最大变形量为0.088264mm。本课题设计矫直精度要求≤0.3mm/m，说明管材在矫直过程中能正常运转，而且也能达到要求的矫直精度。

3.5.2凹凸辊矫直管材变形分析

中间一对辊子主要起到反弯作用，两边的辊子的应力相对中间的凹凸辊子小。对薄壁管材的变形进行了相应的变形分析，同样时间步长取0.0001s，通过对中间凹凸辊进行矫直过程的动态仿真分析，获得该薄壁管材的变形云图，见图11。

图11 薄壁管材变形云图

由管材变形云图可以看出管材在矫直过程中，变形主要在管材径向方向。分析的管材的变形最大为0.085468mm。本文设计矫直精度要求≤0.3mm/m，说明管材在凹凸辊矫直过程中能正常运转，也可达到一定矫直效果。