某下穿铁路U形槽结构设计及数值分析

2019-04-18宋志刚

铁道勘察 2019年2期

宋志刚

(中铁工程设计咨询集团有限公司太原设计院，山西太原 030000)

当前，在公路、铁路及市政道路等工程建设中，出现了大量的下穿立交工程[1]。在地下水位较高或地下水丰富的地区，U形槽结构得到了广泛应用。U形槽结构主要通过边墙抵抗墙背压力，通过结构、附属设施自重抵抗浮力，通过底板、边墙阻止本体外地下水的侵入，从而保证结构的稳定性和耐久性[2]。

目前，U形槽结构分析的主要方法有解析法与数值法。解析法是将结构边墙和底板分开计算，边墙按照浸水地区悬臂挡墙考虑，底板按照弹性地基梁(梁与地基共同作用)考虑[3-5]；但其未能考虑U形槽结构的整体抵抗荷载能力，不能直接算出结构各位置的变形、位移，具有一定的应用局限性。数值方法能够较全面地模拟分析U形槽结构各工况下的受力、变形情况，克服了传统分析方法的不足[6-9]，以下拟通过数值分析研究，总结U形槽结构位移变形、地基反力及结构弯矩的变形规律，对比分析其与解析方法的异同。

1 工程概况

该工程位于既有南同蒲铁路，为平交道口改下穿立交工程。引道走向与铁路一致，西侧引道外为某改移省道，公路外侧为汾河河滩，东侧引道外为某煤矿职工生活小区。

1.1 工程地质和水文地质

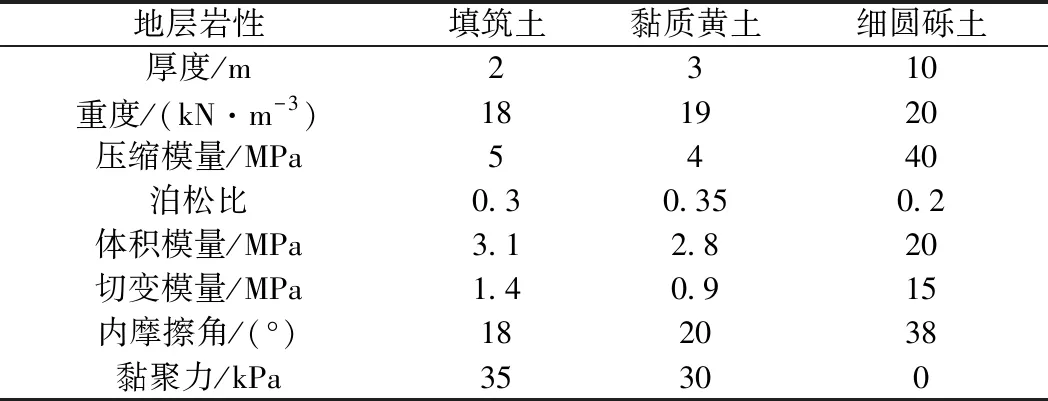
该工程位于汾河河漫滩之上，地形较为平坦，地面高程约为532.1 m。主要地层有：①填筑土(Q4ml)，中密，稍湿，成分以砂质黄土及碎石土为主，厚2～3 m；②黏质黄土(Q4al)，硬塑，层厚0.8～3.1 m；③细圆砾土(Q4al+pl)，中密，稍湿-饱和，层厚5.8～10 m。

地下水以松散岩类孔隙水为主，属潜水。地下水稳定水位为524.15 m。场地位于汾河河漫滩，临近汾河主河道，地下水位受河水影响较大，考虑到季节变幅、汾河洪流等综合因素的影响，地下水位变幅取523.15～526.65 m。

1.2 槽体尺寸

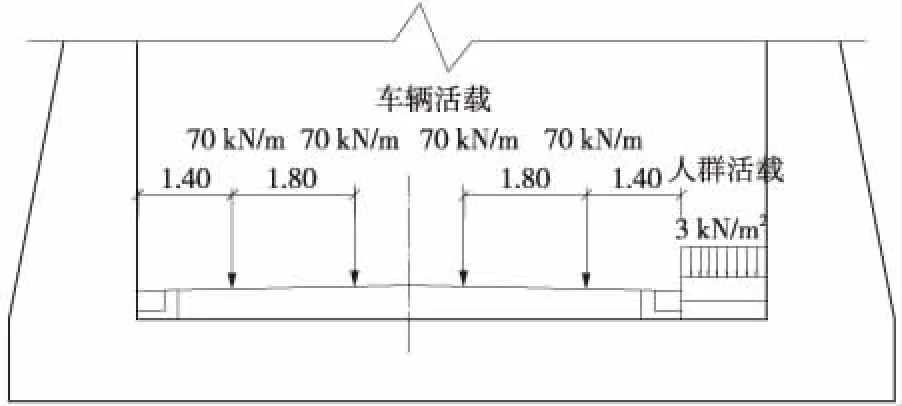
因地下水位高于下穿段路面设计高程，故引道部分地段设U形槽进行防护。结构底面净宽9.25 m，底板宽13 m，厚1.2 m；边墙高7.5 m，顶面宽0.4 m，内侧竖直，外侧边坡坡率为1: 0.20。公路路面宽8.0 m，为双车道设计，机动车路面采用C25素混凝土垫层，厚0.4 m，人行道宽1.25 m，结构横断面示意见图1。

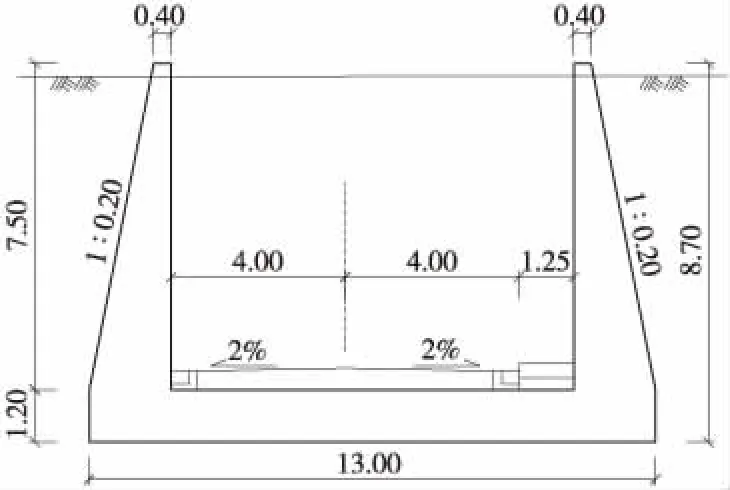
图1 U形槽结构横断面(单位：m)

1.3 结构参数

(1)结构采用C35混凝土，容重γ=25 kN/m3，

(2)路面垫层厚度为0.4 m，采用C25混凝土浇筑，容重γ=23 kN/m3；右侧人行道采用C25混凝土铺设，高出路面0.2 m，宽1.25 m，容重γ=23 kN/m3。

(3)根据《公路桥涵设计规范》[10]，车辆荷载标准值取后轴轴载(140 kN)，按集中力考虑；车辆荷载立面、平面尺寸参照《公路桥涵设计规范》之图4.3.2-1；人群荷载标准值取3.0 kN/m2，均布作用在人行道上。

(4)墙后回填黄土及部分圆砾，内摩擦角φ=30°，填土与墙背摩擦角δ=φ/2=15°，容重γ=18 kN/m3，饱和容重γsat=20 kN/m3。

(5)墙底置于细圆砾土层，地基基本承载力容许值fa0=500 kPa，墙底摩擦系数为0.4。

(6)边墙背侧设计低水位为9.0 m(距墙顶)，设计高水位为5.5 m(距墙顶)。

2 U形槽设计及验算

2.1 计算模型选取

针对U形槽结构特点，取纵向单位长度进行简化计算[11]。边墙按一般刚性悬臂式挡土墙考虑，主要承受侧向土压力、水压力荷载，按受弯构件进行内力及配筋计算[12]；底板按弹性地基梁考虑，主要荷载包括结构自重、浮力、垫层自重、边墙传递荷载及机动车人群活载等[1]。另外，其结构尺寸还应满足抗浮及地基承载力的验算要求。

2.2 抗浮验算

进行抗浮稳定性检算时，设计水位应采用最高水位，抗浮荷载只计主体结构自重。抗浮稳定安全系数为主体结构自重与所受浮力的比值，其值不应小于1.05[2]，其计算公式为

(1)

式中，Gk为结构自重/kN；Flk为结构主体所受浮力/kN；γ为荷载分项系数，一般取0.9。

对于本工程，主体结构自重为968.01 kN，所受浮力为411.08 kN，Kf=2.35，满足设计要求。

2.3 地基承载力验算

一般情况下，U形槽结构自重小于与其同体积的原状土自重，地基承载力能够满足设计要求。当地基为软土层时，应进行地基承载力验算。检算时采用设计低水位，考虑车辆和人群活载作用[13]，检算公式为

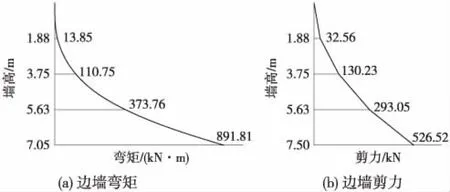
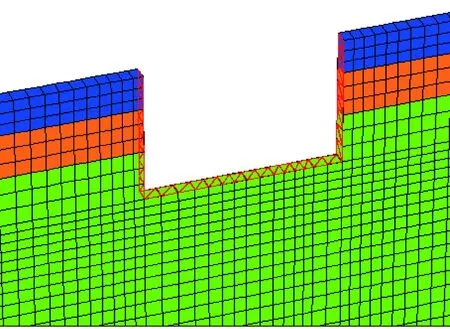
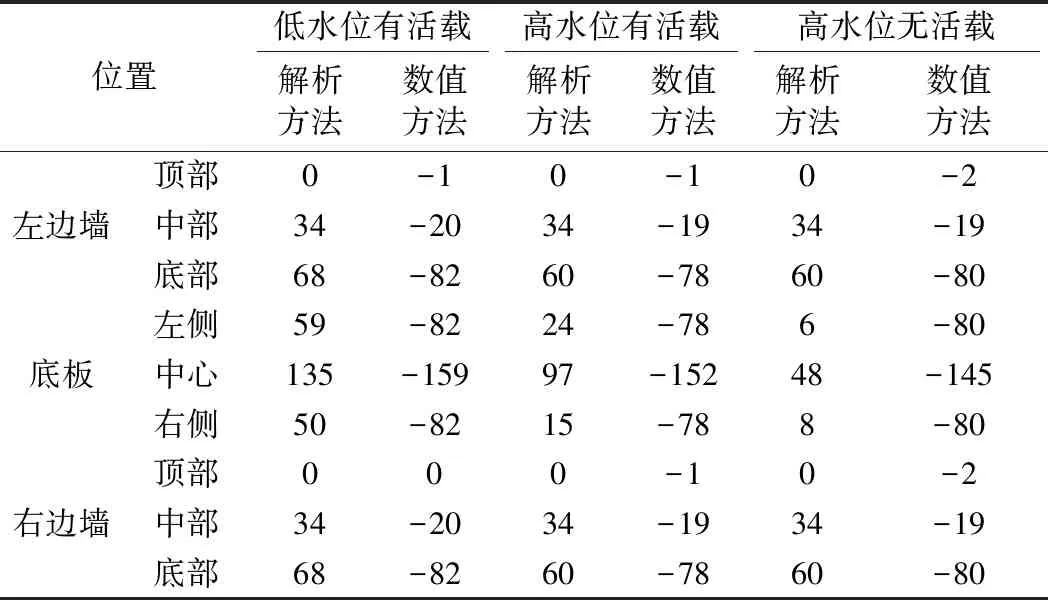
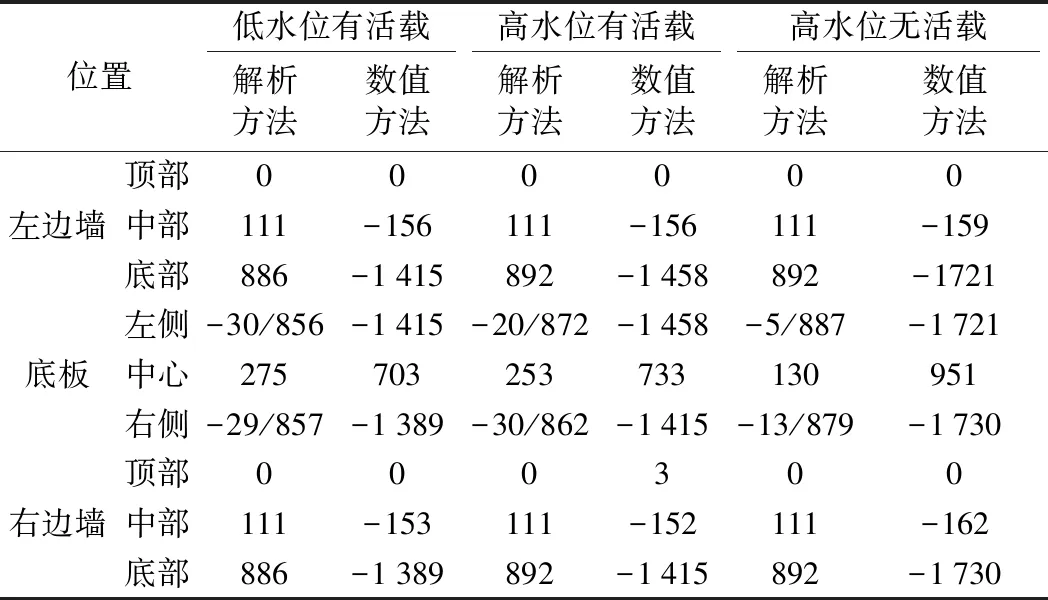
式中，Pz为底板底面地基附加应力值/kPa；faz为底板底面经深度修正后的地基承载力特征值/kPa。

经计算，该U形槽底板底面附加应力值为96.3 kPa，远小于修正后的地基承载力特征值(654 kPa)，地基承载力满足要求。

2.4 边墙强度计算

边墙按悬臂式挡土墙考虑，并采用设计高水位(设计低水位一般不具控制作用)。边墙荷载主要包括边墙自重，边墙墙背土、水压力[11]。边墙自重按初步拟定尺寸计算，墙背土压力和水压力一般采用“水土分算”和“水土合算”两种方法。对于黏性土等渗透性较弱的土质采用“水土合算”，对于砂土等渗透性较强的土质采用“水土分算”[14]。另外，由于结构与土体基本无相对位移，可采用静止土压力形式进行计算[15]。

根据上述设计方法，对边墙进行受力分析，其弯矩及剪力如图2所示。

图2 边墙弯矩及剪力

根据内力计算结果，对边墙进行截面抗弯、抗剪强度检算和裂缝宽度验算。最终确定边墙外侧受拉钢筋选用φ25@100，内侧受压钢筋选用φ12@100，箍筋选用两肢φ14@200。裂缝宽度0.043 mm<0.2 mm，满足规范要求。

2.5 底板强度计算

底板按弹性地基梁(梁与地基共同作用)考虑，其承受荷载包括结构自重、浮力、端部弯矩、车辆及人群活载等。边墙底部截面的弯矩(作为集中弯矩荷载)施加在两者连接处(按刚性连接考虑)[11]。车辆及人群活载参考《公路桥涵设计规范》[10]取值，车辆荷载应按作用在最不利位置处考虑，并按该工况对底板进行强度计算。底板的计算荷载组合应考虑各种外力的最不利组合，一般为四种情况：设计低水位有活载、设计高水位有活载、设计高水位无活载、设计低水位无活载(不具控制作用)。

对前三种荷载组合下的底板内力进行计算(车辆活载按图5位置施加)，内力值：高水位无活载>高水位有活载>低水位有活载。高水位无活载工况下底板内力如图3所示。根据受力情况，进行底板抗弯、抗剪强度检算及裂缝宽度验算。根据检算结果配筋如下：底板下部纵筋选用φ30@100，上部纵筋选用φ18@100，箍筋选用两肢φ12@200。

图3 底板弯矩及剪力

3 数值分析

3.1 结构建模及参数

利用FLAC3D软件的有限差分法进行数值模拟分析。取沿引道方向单位长度1 m进行分析研究，地基本构采用Mohr-Coulomb模型[16]，地基模型宽100 m，深50 m，纵向长1 m。地基位移约束情况为：底面固定、顶面自由，侧面约束法向位移[6]。地下水采用孔隙水压力模拟，U形槽结构采用衬砌(Liner)单元模拟。根据结构实际尺寸，对边墙、底板进行不同衬砌厚度赋值。土层计算参数见表1，衬砌结构单元参数见表2，结构模型见图4。

表1 土层计算参数

表2 U形槽结构单元(衬砌结构单元)参数

图4 U形槽结构模型

3.2 荷载施加

按照三种荷载工况对U形槽结构进行数值分析。恒载主要包括U形槽结构自重、浮力、垫层重力及人行道重力，活载主要为车辆荷载及人群荷载。荷载工况主要分为低水位有活载、高水位有活载与高水位无活载三种，活载施加位置见图5。

图5 U形槽活载施加位置

3.3 结果分析

数值结果分析主要包括槽周土体位移、地基反力及槽身弯矩。

(1)槽周土体位移分析

各荷载工况下槽周土体位移见图6。

三种荷载工况下槽周土体位移呈现以下特征：

① 边墙土体位移普遍较底板位移小，尤其在水位以上的部位。三种工况下，低水位有活载时位移较大，高水位无活载时次之，高水位有活载时最小。由图6可知，水位对边墙土体位移影响较大，活载对边墙位移影响较小。

② 三种工况下，底板土体位移均向上呈马鞍形分布，中部较大，两侧较小。三种工况下，底板土体最大位移均在2 mm左右，相差不大，说明活载及水位对底板土体位移的影响主要体现在位移分布形状上，对位移数值影响较小。

(2)地基反力分析

三种荷载工况下地基反力见图7。

图6 槽周土体位移(单位：m)

注：FLAC3D规定压应力为负值。图7 地基反力(单位：Pa)

图8 结构弯矩(单位：N·m)

三种荷载工况下地基反力有以下特点：

①边墙地基反力自上而下随深度增加而增大，同时，下部较上部的地基反力变化率也较大。三种荷载工况下，边墙同一位置处地基反力数值相近。

②三种工况下底板地基反力变化规律相同，由边墙至底板中心呈马鞍形分布，在大致距边墙1/4底板长度的位置达到最大值。由边墙至底板中心，反力变化速率由急剧趋于平缓。三种荷载工况下，低水位有活载时反力较大，高水位有活载时次之(与无活载时相差不大)，高水位无活载时最小。说明底板地基反力值随水位深度增加而增大。

(3)结构弯矩分析

三种荷载工况下结构弯矩见图8。

三种荷载工况下结构弯矩有以下特点。

①边墙弯矩自上而下数值增大，且下部变化较为显著，最大值出现在墙底与底板交界处。三种荷载工况下边墙弯矩变化趋势一致：高水位无活载>高水位有活载>低水位有活载，表明水位及活载对边墙弯矩均有影响。

②底板弯矩最大值出现在边墙及底板跨中位置，边墙弯矩为负，底板跨中位置为正，零弯矩点出现在边墙至跨中1/3距离处。三种荷载工况下，高水位无活载时最大正弯矩值最大，低水位有活载时次之，高水位有活载时最小。

4 数值分析与解析方法对比分析

4.1 结构变形

数值分析中，认为槽周土体变形等同于结构变形。数值分析是将整个结构作为整体进行计算，可以直接得到结构的变形值。而解析法将边墙、底板分开考虑，无法得到结构各位置的变形值。

4.2 地基反力

三种荷载工况下，两种方法地基反力如表3所示。

表3 U形槽地基反力分析结果 kPa

通过对表3的分析可知：

(1)对于边墙地基反力，两种方法结果较为接近。解析方法中边墙地基反力与水位有关，而与荷载无关，而数值分析结果显示，边墙地基反力与荷载有弱相关，但影响极为轻微，可忽略不计。

(2)对于底板地基反力，二者变化规律基本一致，但数值相差较大(数值方法要大于解析方法)。三种工况下，底板同一位置处，解析算法得到的地基反力变化较大，而数值分析得到的地基反力变化较小。究其原因，数值分析方法将整个U形槽结构体视为一个刚性整体，整体刚度较大，地基反力较小。而解析算法将底板单独考虑，在水位及荷载作用下产生的地基反力就较大。

4.3 结构弯矩

三种荷载工况下，两种方法结构弯矩如表4所示。

表4 U形槽结构弯矩分析结果 kN·m

通过对表4的分析可知：

(1)解析方法的边墙弯矩较数值分析方法普遍较小。解析方法中边墙弯矩与水位有关，而不考虑底板荷载的影响；而数值分析方法结果显示，边墙弯矩不仅与水位有关(高水位工况数值大于低水位工况数值，与解析方法趋势一致)，并且随着底板活载的施加而减小。两种分析方法的差异主要在于解析方法将边墙单独作为悬臂墙计算，而数值分析方法将边墙、底板作为整体计算(考虑了底板荷载对边墙内力的传递)。

(2)两种方法得到的底板弯矩变化规律基本相同，基本呈马鞍形分布，底板弯矩最大值均出现在边墙及底板跨中位置。不同的是，解析算法中边墙与底板跨中位置弯矩值符号相同，而数值分析方法中则恰好相反。这说明二者的数值差异较大，分析其原因：数值分析将底板与边墙作为刚性体整体计算，而解析算法仅仅考虑了边墙荷载对底板的传递，并未考虑边墙在底板抵抗荷载时的协同作用。