障碍空间中基于网格的不确定数据聚类算法*
2019-04-18崔美玉何云斌
崔美玉,万 静,何云斌,李 松
哈尔滨理工大学 计算机科学与技术学院,哈尔滨 150080
1 引言
近年来,数据挖掘[1]技术受到越来越多人的关注,聚类[2]分析也成为了最近几年研究的热点。聚类分析是一种分析数据间关系的无监督方法,是数据挖掘的预处理步骤,它将数据最终划分成多个聚簇,使每个聚簇内的数据对象之间的相似性较高,而簇与簇之间的相似性较低。聚类分析应用在很多领域,例如图像模式识别、传感器网络[3]等。
聚类分析算法主要有基于划分的(如K-means、UK-means[4])、基于密度的(如DBSCAN(density-based spatial clustering of applications with noise)[5]、FDBSCAN(fast density-based spatial clustering of applications with noise)[6])、基于层次的(如 HDCA(hierarchy distance computing based clustering algorithm)[7])和基于网格的(如IGrid[8])等。文献[9]提出了核聚类算法,通过对样本特征的优化,使得算法收敛速度加快,性能得到了较大的改进。文献[10]提出了一种基于原型的凝聚层次聚类U-AHC(uncertain-agglomerative hierachical clustering)算法,采用了信息论和期望距离来比较不确定数据对象。文献[11]提出了PDBSCAN(paralell density-based spatial clustering of applications with noise)算法,通过定义分层密度、模糊核心距离和模糊可达距离来解决自适应阈值的问题。
由于现实生活中,存在一些地理条件的限制(如湖泊、建筑、车辆等),因此在进行相似性度量时,需要考虑障碍的存在,以上算法并没有考虑到障碍的存在。文献[12]提出的带障碍约束的聚类算法实用价值更高。
由于在采集时数据会受到周围环境的影响,因此数据具有不确定性[13],不确定数据的聚类[14-16]研究也成为了热点。现实生活中的障碍物也不可能一直静止不变,空间障碍物可能会发生动态改变,如建筑物的拆迁、楼盘的新建或者车辆的移动等,这些障碍物的改变可能使得原有聚类结果发生改变,因此静态障碍空间和动态障碍空间下的不确定数据聚类的研究有着重大的意义。
现有的数据聚类研究成果大多都是针对确定数据的聚类问题,因此本文解决的是障碍空间中的不确定数据聚类问题,利用网格对数据进行划分。根据障碍集合是否变化提出了静态障碍环境下的不确定数据聚类算法和动态障碍环境下的不确定数据聚类算法,其中动态障碍环境分为障碍动态增加、障碍动态减少、障碍动态移动三种情况。
2 定义与性质
不确定数据点集用X={X1,X2,…,Xn}表示,其中pi为概率值;网格空间由S={S1,S2,…,Sm}组成;障碍集用O={O1,O2,…,Om}表示。文献[17]对数据空间进行了均匀网格划分;文献[18]给出了聚簇代表点质心Ci的定义;文献[19]给出了数据点之间可视性的定义。基于以上定义,本文进一步给出如下定义。
定义1(KL距离[18])KL距离衡量的是空间里的两个概率分布的差异情况,KL距离函数表达式为:
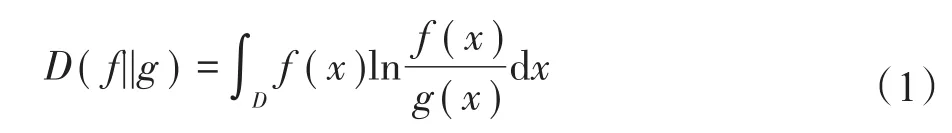
在连续的定义域D中,不确定数据用概率密度函数(probability density function,PDF)表示,连续域下的KL距离表达式为:
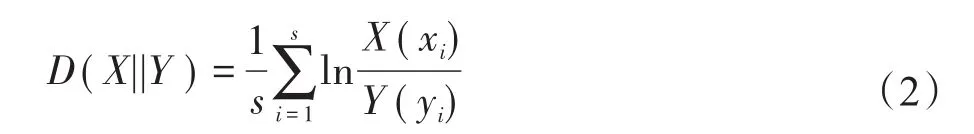
在离散的定义域D中,不确定数据用概率质量函数(probability mass function,PMF)表示,离散域下的KL距离表达式为:

定义2(聚类半径R[18])聚簇网格内所有不确定数据点与代表点Ci的KL距离的均值,即为不确定聚类半径,聚类半径R表达式为:
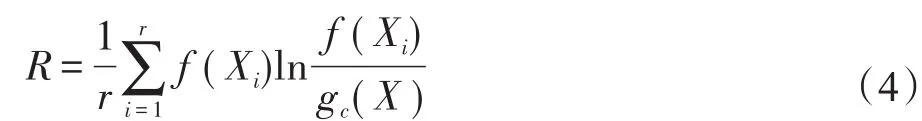
定义3(密度阈值ε)

其中,n表示不确定数据总数,m表示单元网格总数。假定单元网格内不确定数据点的数目大于ε时为稠密网格;单元网格内不确定数据点的数目小于ε时为稀疏网格。
定义4(不确定数据点之间的障碍距离)给定障碍集O,数据点Xi和Ci,Xi和Ci之间互为可视时,表示为D(Xi||Ci)。当Xi和Ci之间不可视时,表示为dist(Xi,Ci),两个数据点之间的障碍距离是绕过障碍的路径最小距离,障碍距离如图1所示。

Fig.1 Example of definition 4图1 定义4的示例

3 算法描述
由于现实生活中障碍物的位置、数量可能会发生变化,因此根据障碍集合是否发生变化分别解决静态障碍和动态障碍空间下的不确定数据聚类问题。
3.1 静态障碍空间下不确定数据聚类算法
本节研究的静态障碍物环境指的是空间障碍物的位置、点集和边集都不会发生改变。
规则1假定稠密网格内可视集合为P1,不可视集合为P2。若Count_P1≥ε,说明稠密网格内的数据在进行相似性度量时大多计算的是直接距离,障碍对数据可视性影响较小。若Count_P2≥ε并且Count_P1<ε,说明稠密网格内的数据在进行相似性度量时计算的是障碍距离,网格内的障碍对数据可视性影响较大,由于障碍距离必然大于可视时的直接距离,因此将此时的稠密网格加入到备选集T2中。
算法的主要步骤:首先根据文献[17],计算步长t,然后计算每个网格的密度ρ,假定可视集合为P1,不可视集合为P2,对集合P1中的不确定数据利用式(2)或者式(3),集合P2中的不确定数据利用式(6)计算;最后根据网格的邻接特性,最终实现不确定数据的聚类,邻接网格的示例如图2所示。
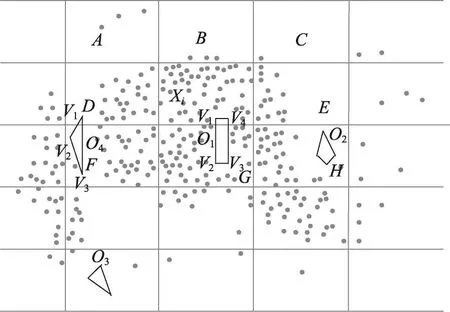
Fig.2 Example of adjacency grid图2 邻接网格的示例
不确定数据点Xi所在网格的邻接网格为A、B、C、D、E、F、G、H。
基于以上的分析和讨论,进一步提出静态障碍环境下基于网格的不确定数据聚类STA_GOBSCAN算法,如算法1所示。
算法1STA_GOBSCAN(X,O,Eps)

3.2 障碍物动态增加情况下的不确定数据聚类算法
算法1解决了静态障碍物情况下的不确定数据聚类问题,由于现实生活中的空间障碍物可能会发生动态改变,因此提出障碍物动态变化情况下的不确定数据聚类算法。
规则2首先定位新增障碍的位置,判断新增障碍的加入是否改变了网格中不确定数据点之间的可视性,若没有改变可视性则调用算法1;若新增障碍的加入,改变了不确定数据点之间的可视性,则只需重新判断由可视的不确定数据点变为不可视集合中的不确定数据点的聚类结果是否改变。
假定障碍动态增加之前可视集合为P1,不可视集合为P2;对应的障碍物新增加之后的可视集合为P1′,不可视集合为P2′。
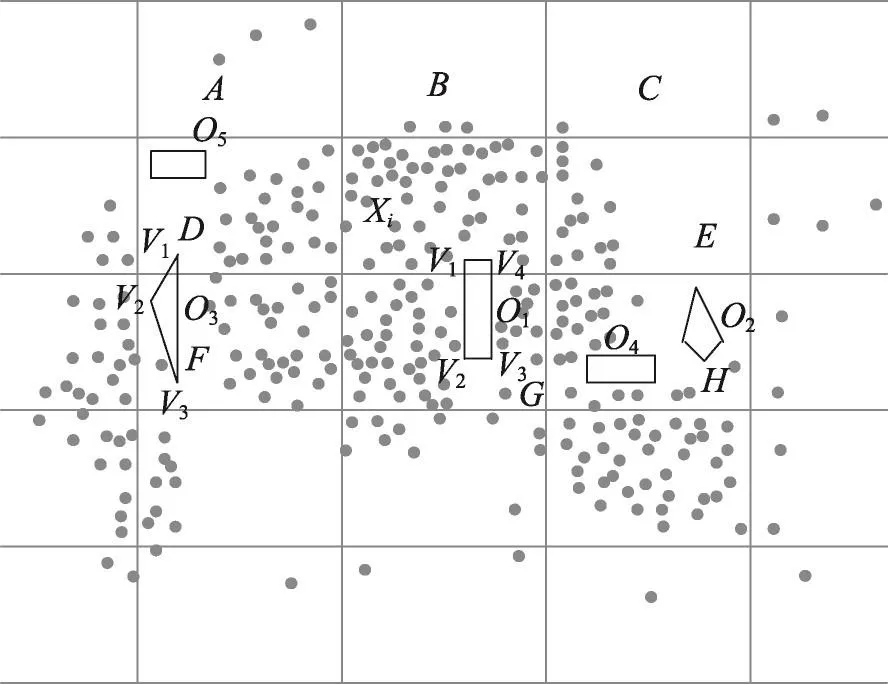
Fig.3 Example of dynamic increase of obstacles图3 障碍物动态增加的示例
如图3所示,不确定数据Xi所在的邻接网格中,原始障碍集合为O={O1,O2,O3},新增障碍O4和O5之后,Onew={O1,O2,O3,O4,O5}。障碍O4的动态加入,使得网格H中部分数据变得不可视,P1>P1′并且P2<P2′,因此障碍O4的动态加入对聚类结果产生了影响。障碍O5的动态加入,不确定数据点之间依然是互为可视的,P1=P1′并且P2=P2′。综上分析,新增加的障碍可能对聚类结果产生影响,也可能对聚类结果没有影响。规则2通过判断新增障碍所在的局部网格空间中的不确定数据点来代替全体数据点的重新聚类,减少了大量的障碍距离的判断,使得算法的效率提高。
基于以上分析,进一步提出障碍物动态增加情况下的不确定数据聚类DYN_GOCBSCAN算法,如算法2所示。
算法2DYN_GOCBSCAN(X,O,Oi)

3.3 障碍物动态减少情况下的不确定数据聚类算法
由于空间障碍物的数量可能发生变化,空间障碍物的减少可能使得原始的聚类结果发生改变。如图4所示,当障碍物减少时,障碍集标记为Onew,其中Oi为减少的障碍物。在障碍物动态减少之前,可视点集合为P1,不可视集合为P2。在障碍物动态减少之后,可视点集合标记为P1′,不可视点集合为P2′。
规则3首先定位动态减少的障碍物的位置,得到障碍物动态减少前的P1和P2,障碍物动态减少后的P1′和P2′。若动态减少的障碍物没有改变网格中不确定数据的可视性,则调用算法1;若动态减少的障碍物改变了不确定数据的可视性,则只需重新判断障碍减少时由不可视变成可视时集合中的不确定数据点的聚类。
如图4所示,动态减少的障碍用虚线表示,假设原始障碍集合O={O1,O2,O3,O4,O5},动态减少的障碍为O4和O2,Onew={O1,O3,O5}。障碍O2的动态减少,并没有改变网格H中的数据间的可视性,P1=P1′并且P2=P2′,聚类结果没有改变。障碍O4的动态减少,使得P1<P1′并且P2>P2′,因此聚类的结果发生改变,判断障碍动态减少的位置是有必要的。

Fig.4 Example of dynamic reduction of obstacles图4 障碍物动态减少的示例
算法的主要思想:障碍物的减少对不确定数据聚类的影响是局部的,规则3对障碍物动态减少前后的可视集合和不可视集合的变化进行分析,并对减少的障碍物不改变聚类结果的情况调用算法1。
基于以上分析,本节提出了障碍物动态减少时的不确定数据聚类算法DYN_GORBSCAN,如算法3所示。
算法 3DYN_GORBSCAN(X,O,Oi′)


3.4 障碍物移动情况下的不确定数据聚类
本节中的障碍物移动指的是障碍物的大小、数量不发生改变,只是障碍物的位置发生改变。
规则4假设障碍物由位置A移动到位置B,在位置A时,障碍物标记为Oib,障碍物的变化情况相当于障碍物动态减少的情况,因此需要分析障碍物动态减少的情况;在位置B时,障碍物标记为Oia,相当于障碍物的动态增加,因此需要分析障碍物动态增加的情况。综上分析,障碍物的移动可以分解成障碍物的动态减少和障碍物的动态增加两部分。
如图5所示,用带箭头的虚线表示障碍移动的前后位置变化情况,障碍物移动之前标记为Oib,障碍物移动之后标记为Oia。

Fig.5 Example of dynamic movement of obstacles图5 障碍物移动的示例
根据障碍物动态移动的前后位置,可以分为以下4种情况:(1)在以网格质心Ci为中心,聚类半径R为半径的覆盖圆内,障碍物Oi在覆盖圆内移动,动态移动后的障碍集为Onew=O-Oib+Oia,如图5障碍O4移动到O6的情况。(2)障碍物Oi由覆盖圆内移动到覆盖圆外,则Onew=O-Oib,如图5障碍O4移动到O7的情况。(3)障碍物Oi由覆盖圆外移动到覆盖圆内,则Onew=O-Oib+Oia,如图5障碍O8移动到O9的情况。(4)障碍物Oi在覆盖圆外移动则Onew=O-Oib,如图5障碍O8移动到O10的情况。
基于以上的分析,进一步给出障碍物动态移动情况下的不确定数据聚类DYN_GOMBSCAN算法,如算法4所示。
算法4DYN_GOMBSCAN(X,O,Oi)


3.5 障碍空间中的基于网格的不确定聚类算法
本节研究的G_OBSCAN算法主要整合了前四节的算法,使得最终的算法可以高效地解决静态障碍空间和动态障碍空间中的不确定数据的聚类问题。
算法的主要思想:首先判断障碍集合的变化情况,若满足O=Onew,则表示障碍是静止不变的,调用算法1;如果满足O≠Onew,则表示障碍物是动态变化的,需进一步判断是障碍的数量发生改变还是障碍的位置发生改变。若只是障碍的位置发生改变,则表示障碍物是移动状态,需要调用算法4来解决,若是障碍的数量发生变化,则需要调用对应的算法2或者算法3来解决。
基于以上分析,给出障碍空间中基于网格的不确定聚类算法G_OBSCAN,如算法5所示。
算法5G_OBSCAN(X,O,Onew)


4 实验比较与分析
由于现有的研究成果大多处理的是静态障碍空间中的不确定数据聚类问题,而没有研究障碍动态变化时的不确定数据聚类问题。为了验证本文方法的有效性和准确性,根据障碍集合是否发生改变,对文献[19]所提的OBS_UK_means算法进行处理。若障碍集合不发生任何改变,则不需要对OBS_UK_means算法进行任何处理,并与本文提出的STA_GOBSCAN方法进行实验对比;若障碍集合发生了改变,可以分为以下障碍动态增加、障碍动态减少和障碍移动3种情况。
(1)障碍集O≠Onew,并且 Count_O<Count_Onew时,表示障碍物动态增加,对障碍集为Onew时调用OBS_UK_means算法。
(2)障碍集O≠Onew,并且 Count_O>Count_Onew时,表示障碍动态减少,对障碍集为Onew时空间中所有不确定数据点调用OBS_UK_means算法。
(3)障碍集O≠Onew,并且 Count_O=Count_Onew时,表示障碍物移动的情况。对移动后的障碍集合Onew重新调用OBS_UK_means算法来实现聚类。
本章主要通过实验对本文所提出的算法进行性能分析与比较,实验硬件环境为8 GB内存,Intel®CoreTMi5处理器,Windows 7操作系统,使用eclipse编译环境,实验使用标准的UCI实验室中的数据集,实验所需数据集的详细情况如表1所示。
实验主要对数据基数n、障碍数、CPU运行时间等几方面进行对比。实验采用Silhouette评测指标(S)作为聚类内部有效性评测,实验采用F-measure熵作为聚类外部评测标准。

Table 1 UCI laboratory datasets表1 UCI实验室数据集
图6给出了不确定数据点规模的增加对CPU执行时间的影响。实验的障碍物数量为100,由图可知,随着不确定数据点规模不断增加,OBS_UK_means算法的CPU执行时间呈急剧上升趋势,而算法STA_GOBSCAN的执行时间上升较缓慢并且执行时间始终少于OBS_UK_means算法。
表2的CPU执行时间为执行50次算法的平均时间,障碍数量初始值为100,当障碍数量增加到110时,OBS_UK_means算法的CPU执行时间大于DYN_GOCBSCAN算法,说明了DYN_GOCBSCAN算法优于OBS_UK_means算法。

Fig.6 Influence ofnon CPU execution time图6 数据量n对CPU执行时间的影响
如表3所示,反映了障碍物动态减少时DYN_GORBSCAN算法与OBS_UK_means算法的CPU执行时间比较,其中障碍数量初始为100,当障碍数量较少到90时,表中算法的CPU执行时间都减少,因为障碍距离的计算比可视距离的计算更复杂,障碍的减少使得部分障碍距离变为直接距离,使得总的计算量减少,所以总的CPU执行时间也减少。由于规则3的提出,判断了障碍减少的情况,障碍的局部处理代替了OBS_UK_means算法的全局重新聚类,因此DYN_GORBSCAN算法的CPU执行时间更少。

Table 2 Comparison of algorithms of obstacles dynamic increase表2 障碍动态增加时的算法比较

Table 3 Comparison of algorithms of obstacles dynamic reduction表3 障碍动态减少时的算法比较
表4展现的是当障碍物动态移动时DYN_GOMBSCAN算法与OBS_UK_means算法的CPU执行时间的比较。由于OBS_UK_means算法分别对障碍移动前和障碍移动后重新聚类,因此OBS_UK_means算法的CPU执行时间大于DYN_GOMBSCAN算法。
如表5所示,分别对算法进行50次独立聚类实验,统计每次实验的结果,并对每种算法求50次实验结果的平均值,对比算法的实验结果。结果显示,对以上4组数据集,本文提出的G_OBSCAN算法的F-measure指标平均值和S指标均值均高于OBS_UK_means算法的评测指标。通过实验可看出,G_OBSCAN算法表现出更好的聚类效果。
通过以上实验分析可知,本文提出的算法均具有较高的效率和准确率。
5 结束语
根据国内外研究发现,传统的聚类算法大多利用欧式距离进行相似性度量,本文主要利用网格对数据空间划分并使用KL散度进行相似性度量。由于现实生活中的障碍可能是动态变化的,因此本文研究了静态障碍空间中和动态障碍空间中的不确定数据聚类问题,通过判断障碍集合的前后变化,提出了G_OBSCAN算法,理论研究和实验分析表明,本文所提算法均具有较高的效率。
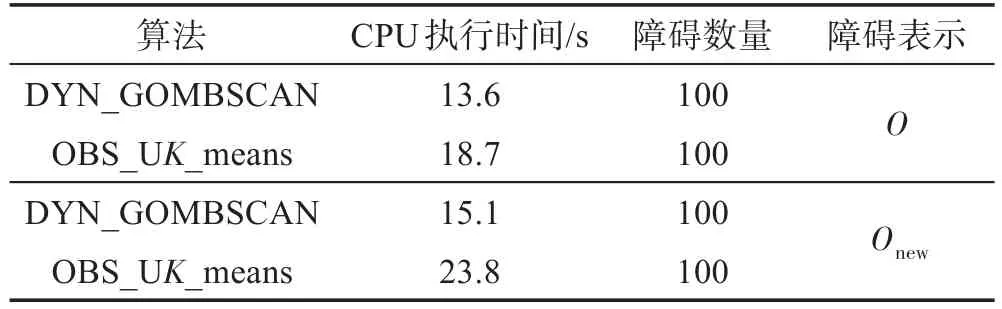
Table 4 Comparison of algorithms of obstacles dynamic movement表4 障碍动态移动时的算法比较

Table 5 Comparison of algorithm effectiveness表5 算法有效性的比较
