多方强隐私保护记录链接方法*
2019-04-18佟丹妮申德荣韩姝敏聂铁铮
佟丹妮,申德荣,韩姝敏,聂铁铮,寇 月,于 戈
东北大学 计算机科学与工程学院,沈阳 110819
1 引言
当今社会,链接来自多方的大型数据库记录的需要日益增加,链接的同时要求保护存储在这些数据库中实体的隐私。为此,呈现出了对PPRL(privacypreserving record linkage)的研究,即不同机构数据库间的记录链接需要满足下述要求:第一,记录中的敏感信息不能透露给记录所有者以外的其他参与方;第二,攻击方不能获取这些敏感数据。PPRL技术可以使数据需求者只在数据库中获取其需要的某些记录的部分属性,来实现隐私保护下数据整合的目的。当前PPRL的研究领域主要包括医疗保健、政府服务、犯罪检测以及商业应用等。例如,医药研究人员为调查新药物的不良反应,需要整合来自不同医院、诊所和药房的数据,在该项研究中,研究人员只获取使用该新药后患者表现出的症状,而不知道患者的其他信息。又如,一个国家的犯罪调查单位需要利用执法机构、互联网服务提供商和金融机构等单位的国家数据库中的机密数据,采用PPRL技术,只获取链接上的记录对应的人员身份信息(如某些可疑人员的身份信息),而不必获取全部数据,这将大大减少隐私泄露的风险。
PPRL技术作为记录链接技术的一个分支研究,主要包括分块和匹配两个阶段。在分块阶段,将相似记录划分在同一分块内,以此减少生成的“候选记录组”数量。在匹配阶段,应用相似度函数对每个候选记录组进行计算,将候选记录组归类为匹配记录组或不匹配记录组。但不同于传统的记录连接,PPRL的两个阶段中都需要考虑额外的隐私保护需求。
然而现有的PPRL分块方法[1-5]均不能使PPRL同时达到高查全率和高查准率,主要源自于如下两方面:一方面,分块后还会生成过多真实情况下并不匹配的候选记录组,造成额外的计算代价;另一方面,分块后损失真实匹配的记录组,未对其进行匹配计算。而已有PPRL中的匹配方法大多适应于两个数据方间的记录链接,而多个数据方间的匹配方法[6-10]均不能同时达到强隐私性和高效性。强隐私保护记录链接可完全防止攻击方的攻击,而现有的多方强隐私保护下的匹配方法均具有很高的匹配计算代价,导致匹配时间过长,使其不适用于大数据环境下的记录链接。
针对已有工作的不足,本文提出了一种多方强隐私保护记录链接方法(multi-party strong-privacypreserving record linkage method,MP-SPPRL),其在大数据环境下同时具有高查全率、高查准率和高效性。本文的主要贡献有:
(1)提出了一种LSH(locality sensitive Hashing)结合后缀的二次分块方法,根据LSH分块后的分块分散度设定后缀分块的后缀长度,使二次分块在保证MP-SPPRL高查全率的前提下提高查准率。
(2)提出了一种基于滑动窗口的多方分块合并方法,提高链接的容错率,进一步保证MP-SPPRL的高查全率。
(3)设计了一种基于SMC的可伸缩多方记录匹配算法,通过缩减同态加密记录数量和提前终止不可能匹配的候选记录组的距离计算,降低匹配的时间代价,使该算法适用于大数据环境下。
(4)通过实验证明,本文提出的二次分块方法可以同时保证MP-SPPRL的高查全率和高查准率,提出的匹配算法相较于已有的利用SMC的匹配方法更高效。
2 相关工作
在PPRL研究领域,文献[11]指出许多分块方法已经被采用。Al-Lawati等人[12]首次把标准分块技术引入PPRL,具有相同BKV(block key value)的记录被分到同一块内,而分块属性将影响生成的候选记录组的质量和数量。基于排序的分块算法[3]根据分块参数排序所有记录,并沿着已排序记录列表滑动一个窗口,所有出现在同一个窗口中的记录被放置在同一分块内,窗口大小决定分块大小以及每个记录将被放置在多少个分块内。Vries等人[2]介绍了基于后缀数组的分块方法,其基本思想是将记录的BKV及其后缀插入到基于倒排索引和字母顺序的列表中,按其对记录进行分块。嵌入式分块方法[3]使用一组参考集来定义嵌入空间,数据方通过计算他们的记录和参考集内记录之间的距离向量来嵌入记录到该空间,如果记录相似,它们与嵌入空间中参考记录的距离向量也会相似。LSH分块方法[4]是一种高效并广泛使用的大数据分块方法,它通过独立且随机地从哈希函数集合中选择函数来映射数据,这些哈希函数对距离度量是局部敏感的,如果用相同函数来哈希两个实体,产生相同结果的概率取决于它们的距离。
由于Bloom Filter可以保持属于不同数据集的原始记录字符串之间的距离(相似度),它是PPRL中广泛应用的编码方式。在Bloom Filter上对记录进行LSH分块是一种流行的方法。Durham[13]首先提出了基于Bloom Filter的LSH隐私分块方法,并通过实验证明了LSH方法的高查全率。Karapiperis和Verykios[4]提出了利用LSH函数分块的PPRL框架,并比较了三种类型的LSH函数,其中Hamming-based LSH表现最好,可以高效地生成候选记录对。在多方分块方面,Ranbaduge等人[14]提出了基于LSH的多方PPRL分块方法。虽然LSH分块方法在PPRL的查全率方面表现优异,但其查准率过低,会造成后续过多不必要的匹配计算。
在PPRL匹配方法研究中,目前的研究大多数是两个数据方间的记录匹配,没有考虑到多个数据方参与可能。在少数多方匹配问题研究中,第一个方法由Quantin等人提出[15],借助第三方来比较记录的哈希编码值,以此对多个数据方的记录进行匹配。文献[16]提出了一种结合动态阈值、检查机制和安全合计的多方近似匹配方法。但这两种方法均不能完全防止攻击方的攻击。SMC(secure multi-party computation)[17]是一种足够安全且计算准确的多方计算方法,能够保证多方PPRL的强隐私性,即能够在某一数据方与攻击方串通的情况下保护链接的隐私性。O’Keefe等人[6]提出了基于SMC的方法,在特定记录传输协议下完成匹配,此方法在实现绝对安全的同时也会导致极高的时间代价。类似地,Vatsalan等人[10]设计的基于SMC的多方匹配算法也存在时间代价大的不足。已有的基于SMC的匹配方法均不能实现可伸缩的PPRL,不适用于大数据环境下。
针对LSH分块方法查准率低的问题,本文提出的LSH结合后缀的二次分块方法,在损失少量查全率的情况下,大幅度提高了查准率,再通过保证链接容错率的基于滑动窗口的分块合并方法生成候选记录组。针对SMC匹配方法存在计算代价大的问题,本文设计了一种适合MP-SPPRL的基于SMC的可伸缩多方记录匹配算法,通过缩减同态加密记录数量和提前终止距离计算机制改善了SMC匹配方法时间代价大的问题,可以在大数据情况下进行MPSPPRL,保证强隐私性同时有效控制链接时间。
3 问题定义
定义1(MP-SPPRL) 对于 来自n个数据方P1,P2,…,Pn的数据集D1,D2,…,Dn,识别出n个数据集中表示同一真实实体的记录组,同时要求没有任何数据方的私密信息泄露给链接过程中的其他数据方和额外参与方Pn+1。
定义2(Bloom Filter序列)对记录属性值Bloom Filter编码后得到的由0和1构成的序列。每条记录对应两个由所属数据方对记录编码得到的Bloom Filter序列,分别是表示记录分块属性值的bf和表示匹配属性值的BF,所有Bloom Filter序列的长度均为L。
在进行分块前,从n个数据方共同拥有的属性中选取出分块属性和匹配属性,需要各数据方用相同的函数各自对记录进行Bloom Filter编码。
定义3(候选记录组)由n条分别来自n个数据方的相似记录r1,r2,…,rn的编号组成的n元组,需要计算此n条记录相互之间的距离,判断此n条记录是否表示同一实体。
本文设计的MP-SPPRL流程如图1所示。首先,各数据方对其数据集Bloom Filter编码;其次,数据方各自对其数据集进行二次分块;接着,一个额外的参与方Pn+1合并各数据方的相似分块,在合并后形成的最终分块内生成候选记录组;最后,n个数据方和Pn+1共同对候选记录组进行匹配,得到匹配记录组集合M。
4 LSH结合后缀的二次分块方法
4.1 二次分块模型
二次分块是指在LSH分块的基础上进行后缀分块。分块过程中各数据方的记录不会传递给其他数据方,可确保分块阶段隐私性。传统LSH方法不能有效地控制分块内记录的数量,会生成较多实际并不匹配的候选记录组,导致查准率较低。本文在LSH方法生成的分块上进行后缀分块,生成新的分块,相较于LSH分块方法提高查准率,同时具有LSH方法查全率高和可以对大型数据集快速划分的特点。
LSH分块:多个数据方确定J组一致的Hash函数Hj,j=1,2,…,J,每组Hj由K个哈希函数构成,k=1,2,…,K。对于每组Hj,n个数据方各自用其进行LSH分块,将每条记录划分到一个分块内。方法是用Hj对记录的bf进行哈希映射,得到长度为K的向量即hash key,向量值相同的记录被分到同一LSH分块内。选择J组函数是为了避免因表示同一实体的记录形式不一致而造成候选记录组损失的情况。
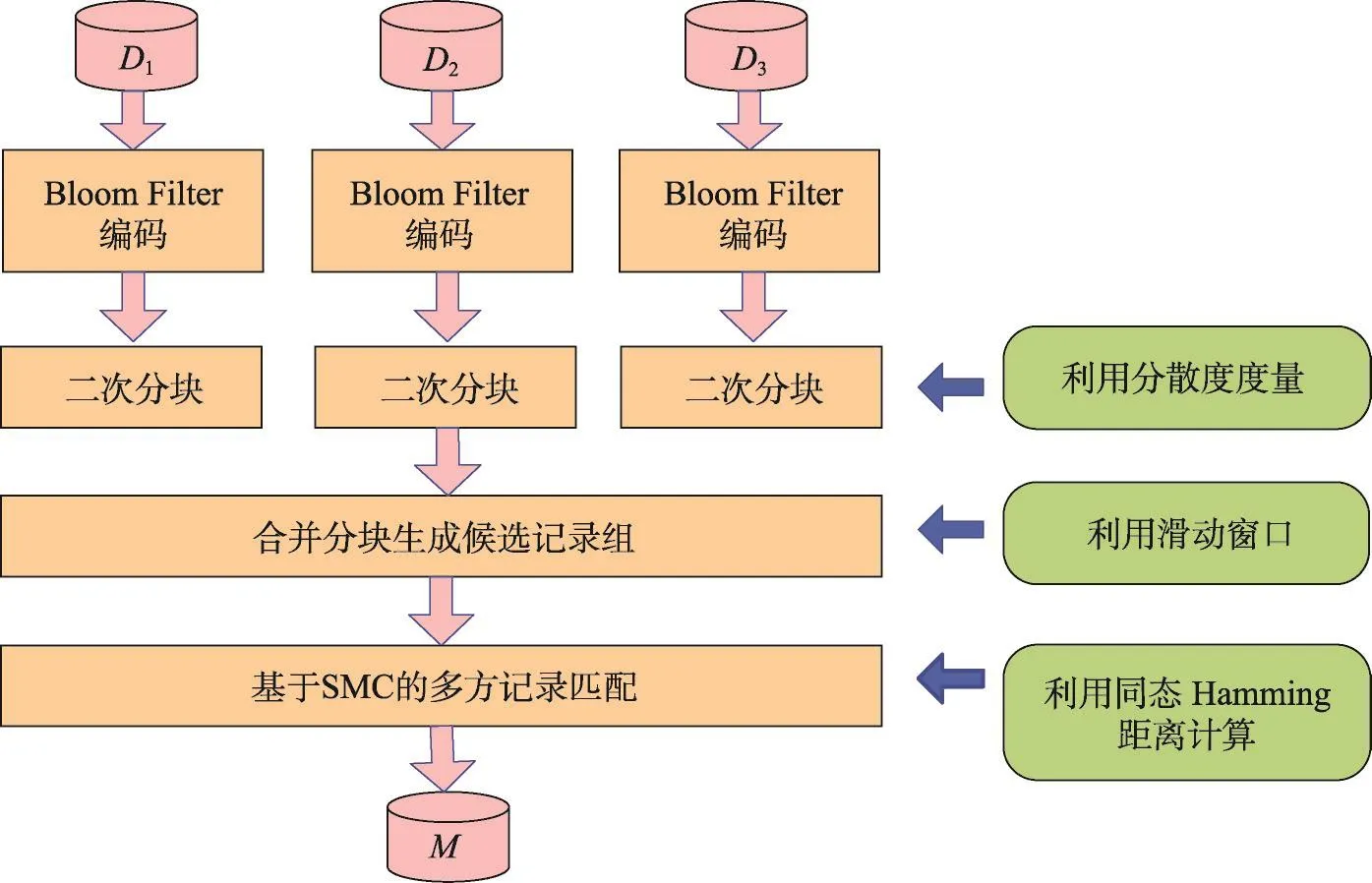
Fig.1 MP-SPPRL process图1 MP-SPPRL流程图
后缀分块:对于每组通过Hj生成的LSH分块,分别利用x种不同长度(lmin,lmin+1,…,lmin+x-1)的后缀对每个LSH分块进行x次后缀分块,每个LSH分块内bf后缀值相同的记录被分到同一个分块内,则二次分块后,一条记录会出现在J×x个分块内。
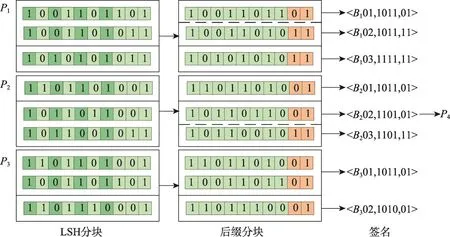
Fig.2 Double blocking process图2 二次分块流程图
二次分块后,一个分块用一个签名<id,LSH-key,suffix>表示,其中id是分块编号,LSH-key是LSH分块过程中对应的向量值,suffix是后缀分块过程中对应的后缀值。各数据方将代表其分块信息的签名及各分块内记录编号传递给额外的参与方Pn+1。
本文利用Hamming LSH方法及其对应的Hash函数hjk(bf)=bf[l],函数映射得到的哈希值为bf的第l个位置的值,l是从区间[0,L)中随机选取的。如图2所示,LSH分块表示的是一组由4个hjk组成的Hash函数Hj对n=3个数据方记录的分块过程,选择的4个哈希函数的l分别是1、3、5、7,如P1中的第一条bf通过Hj得到的向量即为<1,0,1,1>。在后缀分块过程中,后缀长度为2,P1的第一个LSH分块包含两条记录,它们长度为2的后缀值分别是01和11,于是后缀分块后它们属于不同的分块。图2仅为利用一组哈希函数和一种长度后缀的二次分块过程。
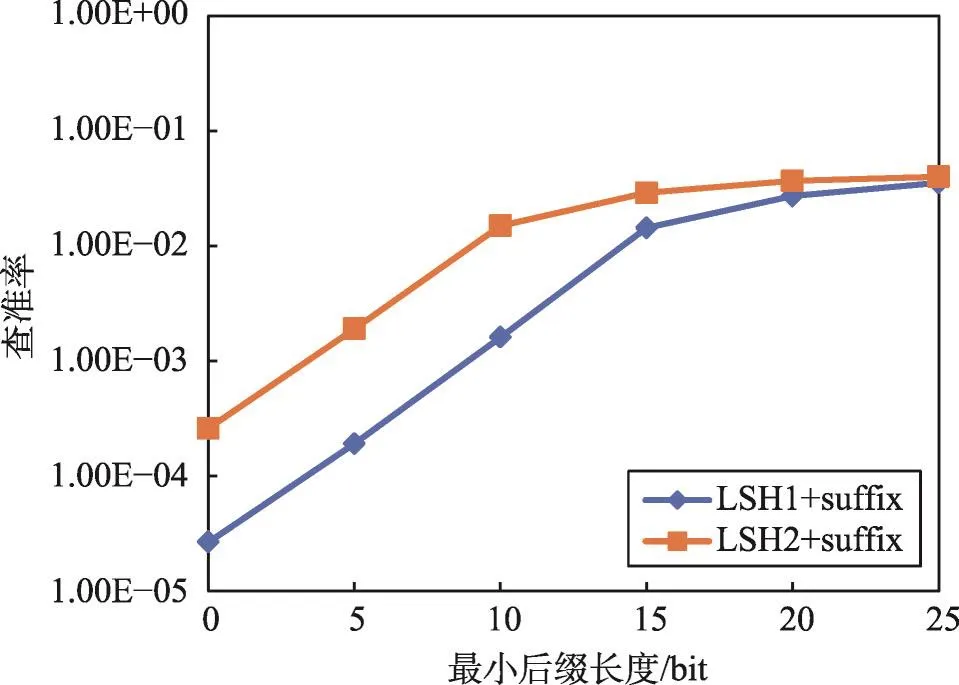
Fig.4 Relationship of precision and lmin图4 查准率与最小后缀长度关系图
4.2 基于LSH分块分散度的后缀长度确定
4.2.1 后缀长度对MP-SPPRL查全率和查准率的影响
图3和图4说明了二次分块中最小后缀长度lmin(x=2)与MP-SPPRL查全率和查准率之间的关系。LSH1+suffix和LSH2+suffix是对同一数据集采用不同的函数进行LSH分块的两种二次分块,lmin为0时等同于只进行LSH分块,lmin大于0时为进行LSH分块和后缀分块的二次分块。在图3和图4中,随着lmin增加,查全率下降缓慢,查准率上升迅速。当lmin达到15后,LSH1+suffix的查全率和查准率都趋于平稳,则对于此二次分块应选择的lmin为15。而LSH2+suffix对应的二次分块适合的lmin为10。可见,不同的LSH分块集群适合不同的后缀长度。
4.2.2 基于信息熵的分块分散度度量模型
本文引入分块分散度度量来确定后缀分块的后缀长度。在LSH分块后,n个数据方记录构成LSH分块集群,可依据表示集群分块内记录差异程度的分块分散度确定后缀长度。分散度足够低说明LSH分块方法已经能够有效地对记录进行划分,若继续划分会造成真实匹配记录组的损失。反之,还可继续划分。二次分块时LSH分块集群的分散度越高,应选取越大的后缀长度。
本文提出基于信息熵的分块分散度度量模型:单块分散度和整体分散度两类。单块分散度由分块所属数据方计算,整体分散度由任一数据方或额外参与方计算。分析含有记录数量过少的分块会造成分析得不准确,分析时应排除此类情况的分块。
每个数据方在其大小大于X的分块中随机选取N个(远小于存在的分块数量),分别从这N个分块内随机选取q条记录(远小于分块内记录总数)。在bf上随机选择m个LSH分块函数不曾作用的位置,连接每条记录bf这m个位置的值形成一个序列,统计一个分块内序列的差异程度。n个数据方应确定一致的x、N、q取值和m个位置。单块分散度如式(1)所示:

其中,j表示n×N个分块中的第j个,。为此分块内I种不同序列出现的概率,i=1,2,…,I。
根据单块分散度计算整体分散度,据此来评估n个数据方综合的分块分散情况,则整体分块分散度如式(2)所示:

通过阈值θ判断是否需要进行后缀分块,θ的取值和数据扰乱程度相关。通过增加LSH中每组Hash函数的个数,确定仅通过LSH分块就达到可接受的查准率时的Hs值为θ。但仅通过LSH分块达到此查准率时对应的查全率远低于通过二次分块达到此查准率时对应的查全率,尤其是数据扰乱比例大的情况下。当LSH分块集群的Hs小于等于θ时,表明LSH方法已经将相似度低的记录划分到不同的分块内,无需进行后缀分块,后续分块合并步骤只需将各方LSH-key相同的分块合并即可。若初步分块的Hs大于θ,则选取的最小后缀长度lmin如式(3)所示:

其中,Ht是对和需要链接的数据集质量相同的数据进行LSH分块后测试得到的整体分散度,lt是Ht对应的最佳最小后缀长度。
4.3 基于滑动窗口的分块合并
由于不同数据方对同一实体的描述方式不一定相同,这可能会导致真实匹配的候选记录组的损失。通过图5来说明分块过程中这一问题。Peter和Pete是P1和P2的两条表示同一实体的记录的分块属性值,它们所属分块的LSH-key相同但suffix不同,合并分块时需要将Peter和Pete所属的两个分块融合在一个最终分块内。为此,本文提出基于滑动窗口的分块合并方法以提高MP-SPPRL的容错率。分块合并步骤是Pn+1利用滑动窗口对n个数据方各自的分块进行融合生成最终分块的过程。然后在含有n方记录的最终分块内生成候选记录组。要求分块合并方法使n方的相似记录存在于同一最终分块内,并避免过多不匹配的候选记录组生成。多方分块合并方法具体如下:
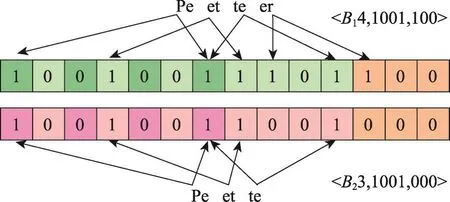
Fig.5 Example of different records for the same entity图5 表示相同实体的不同记录举例
首先,Pn+1统计接收的n方分块签名,对LSH-key相同且suffix长度相同的分块签名按suffix值二进制大小顺序排序形成签名列表。
如图6所示,n=3时,在使用一组Hj的LSH分块和x=2的两次后缀分块后,对LSH-key为1011,suffix长度分别为2和3的两组分块签名排序,并形成两个签名列表(图6中的前5行为第一个签名列表,后7行为第二个签名列表)。
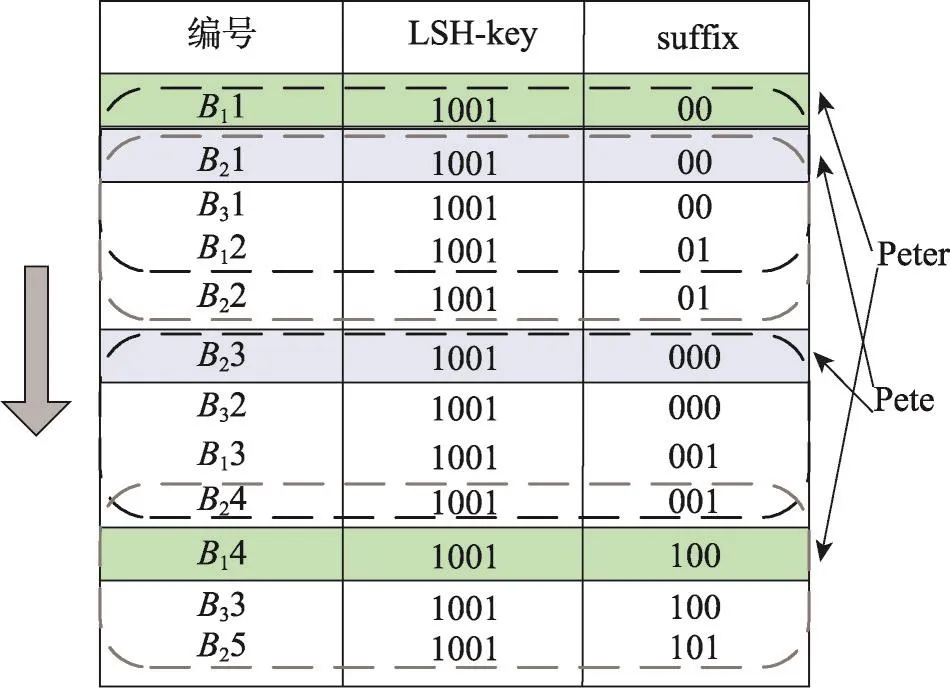
Fig.6 Blocks combining based on sliding window(n=3)图6 基于滑动窗口的分块合并(n=3)
之后,采用大小为w的滑动窗口对每个签名列表进行滑动,在同一窗口内若存在来自n个数据方的分块,此窗口内的所有分块才会被合并生成一个最终分块。最终分块内每n条来自不同数据方的记录组成候选记录组。其中,滑动窗口大小w通过实验测试确定,要求w大于等于n,查全率随w增大而升高,查准率随w增大而降低。
图6中的w为4,suffix长度为2的分块签名列表中有5条分块签名,窗口从顶部向下滑动,每次滑动一行,直至底部,则对于此签名列表,生成两个最终分块,分别由编号为B11、B21、B31、B12和编号为B21、B31、B12、B22的分块合并得到,编号Bij表示数据方Pi的第j个分块。
根据上述方法,发现当用长度为3的后缀进行分块时,图5中两条记录所在的LSH-key相同的分块对应的后缀值分别是100和000,因为后缀值第一个比特位值不同,两个分块排序后会相隔较远,同时存在于滑动窗口内的可能性低,但当用长度为2的后缀进行分块时,两记录所在分块的后缀值均为00,排序后一定会出现这两个分块同时存在于滑动窗口内的情况,并且这两个分块会被合并。以此避免拼写错误等情况造成的真实匹配候选记录组的损失,提高MPSPPRL的容错率。可根据一条记录内拼写错误的平均字符数量确定x和w。
5 强隐私保护下基于SMC的可伸缩多方记录匹配算法
PPRL普遍考虑的攻击模式是HBC(honest-butcurious behavior)[17],即PPRL的参与方均遵守规定的链接规则,但他们试图获取其他数据方的输入信息。在这种攻击模式下,数据方可以和额外的参与方Pn+1串通,从而获取其他数据方的敏感信息。
采用同态加密的SMC匹配方法可以在HBC模式下防止数据方和Pn+1串通引起的攻击,其强隐私性在PPRL中具有很高的应用价值,但同态加密计算方法时间复杂度大,因此之前没有应用在大数据多方PPRL中。
为此,本文提出了一种基于SMC的可伸缩多方记录匹配算法,通过缩减加密时间和提前终止机制,在保证匹配强隐私性的同时大幅度降低时间代价,面对大数据集和数据方个数增加时,具有可伸缩性的匹配算法依然能保证时间代价在可控范围内。
数据集大小均为z,传统SMC方法的加密记录个数为n×z,而本文根据改进的同态加密距离计算[4]两条记录只需加密一条的特点,设计的算法只需选择接近z条记录进行同态加密,各数据方的加密时间约缩减为原来的1/n。加密方指派原则为同一LSH-key值对应的候选记录组中只对一个数据方记录的匹配属性值BF进行同态加密。Pn+1确定各LSH-key值对应的加密方,使得加密时间最长的一方加密时间最小化。提前终止匹配机制是在Pn+1确认候选记录组已不匹配的情况下,Pn+1通知数据方终止不必要的距离计算,缩减候选记录组匹配时间。
本文基于加密方指派原则和提前终止匹配机制,采用同态Hamming距离计算,提出了可伸缩多方记录匹配算法,在一个候选记录组中,若加密记录与其余n-1条记录均相似,则认为这n-1条记录也相互相似,判断此候选记录组为匹配的。记录对相似度sim=1-d/L,因此本文用Hamming距离来判定候选记录对相似性。由于数据质量问题,规定当两记录距离d>T时视此记录对不相似,反之,为相似记录对。阈值T的选取与表示同一实体的记录对匹配属性值可能出现的不同字符数量有关。
算法1可伸缩多方记录匹配算法
1~4行是Pn+1指派各LSH-key值对应的加密方,并将指派结果EncryptingPartyInfo和候选记录组集合G发送给n个数据方。5~6行是数据方根据指派加密BF并传递给其余n-1方。7~14行是根据计算得到的记录间Hamming距离将不匹配的记录组从候选记录组集合G中移除。对于每个Pi不是加密方的候选记录组{r1,r2,…,rn},Pi利用BFi和BFj*计算ri和加密方Pj的记录rj形成的记录对的Hamming距离d∗,多组候选记录组包含相同的记录对,计算一次即可,Pi将d∗传递给Pn+1,Pn+1对d∗解密,如果距离大于阈值T,则判断包含此记录对的候选记录组均不匹配,并通知数据方将它们从候选组集合G中移除,节省数据方不必要的记录组距离计算。15~20行是Pn+1对未被移除候选记录组的核查,如果候选记录组g的加密方记录rk与其余n-1条记录rl,l=1,2,…,k-1,k+1,…,n均进行过距离计算则判定g为匹配的,否则需要完成遗漏的距离计算再判断g是否匹配。最后,仍存在于G的记录组被认定为匹配的记录组,返回匹配记录组集合M=G。
6 实验与结果
6.1 实验设置
(1)实验数据集
本文采用的数据集为北卡罗来纳州选民登记数据集(NCVR),选取记录的姓和名作为分块属性,选取通信地址作为匹配属性,bf和BF长度均为100。
实验环境如下:主机采用Intel®CoreTMi7 CPU,3.4 GHz双核处理器,内存容量为8 GB,操作系统为64位Windows 7。本文用Python(3.6.3)实现文中提出的方法。
(2)评价准则
实验通过查全率(Recall)、查准率(Precision)[3]和运行时间(Runtime)评价二次分块方法,通过错误率(Error rate)和运行时间(Runtime)评价可伸缩多方记录匹配方法,并与已有的分块及匹配方法进行对比评估。
查全率是候选记录组中真正匹配的记录组数量与数据集中真正匹配的记录组数量的比率(见式(4))。

查准率是候选记录组中真正匹配的记录组数量与候选记录组数量的比率(见式(5))。

其中,TP是实际匹配的候选记录组数量,FP是实际不匹配的候选记录组数量,FN是由于分块步骤损失的实际匹配的记录组数量。
错误率是判定为匹配的记录组集合M中实际不匹配的记录组所占比例,错误率与匹配方法的精确性成反比。
PPRL的运行时间可划分为两阶段。第一阶段为PPRL开始至生成候选记录组所用时间,此段时间可用以评估分块方法的时间性能,所用时间受分块操作简单性和生成的候选记录组数量影响。第二阶段为对候选记录组进行匹配计算至得到匹配记录组集合M所用时间,此段时间可用以评估匹配方法的时间性能,所用时间和匹配方法的计算复杂度有关。
(3)对比方法及参数确定
本文对提出的二次分块方法与已有的LSH分块方法[4]和后缀分块方法[2]进行对比实验,提出的可伸缩匹配算法与已有的利用SMC的匹配算法[10]进行对比实验。实验数据有扰乱比例30%和75%两种,每个数据方的数据集大小为5×103条记录至1×105条记录,数据方个数为3、5、7或9。
表1为仅通过LSH分块方法得到的查全率及查准率,当Hs的值在0.27和0.55之间时,查全率和查准率均趋于平稳,且查准率可以接受,则合适的θ取值应在此范围内。图4和图5已经测试出扰乱比例为30%时两组整体分散度及对应的最佳的最小后缀长度,一组作为计算参数Ht=1.4,lt=15,另一组(1.11,10)用于测试θ取值,在0.27~0.55范围内测试不同的θ值,当θ被设置为0.5时,根据式(3)计算出的Hs=1.11对应的lmin=10.16符合lmin的真实值10,因此本文实验中扰乱比例30%数据的θ=0.5。类似地,设置扰乱比例75%数据的θ=0.3。
实验中的LSH方法和二次分块方法中均选择3组哈希函数,每组20个,选择两种长度的后缀(x=2),通过θ=0.5和θ=0.3确定两种扰乱比例数据对应的后缀长度均为15、16位。后缀分块方法的窗口大小为6,后缀长度为15、16。实验数据集匹配属性值由扰乱最多可造成两个字符的不同,且考虑不同字符映射到Bloom Filter同一比特位的冲突情况,根据测试确定T的最佳值为3。

Table 1 Hs,Recall and Precision of LSH blocking表1 LSH分块的Hs与查全率、查准率
图7为数据方个数不同时,MP-SPPRL的查全率随分块合并方法中滑动窗口大小w增加的变化情况。利用滑动窗口的目的是使各方的相似记录存在于同一分块内,w越大相似记录越可能被聚合在同一最终分块内,查全率越高。因为绝大多数相似记录所在分块在签名列表中位置会相近,w足够大后,绝大数相似记录会被聚合,w继续增大作用很小,对查全率改变并不明显。可以看出对于3、5、7、9个数据方,当w分别达到5、7、9、12后,查全率趋于平稳。同时,查准率一定会随w增加持续降低。因此下面实验中4种数据方个数的MP-SPPRL方法对应的w分别设置为5、7、9、12。
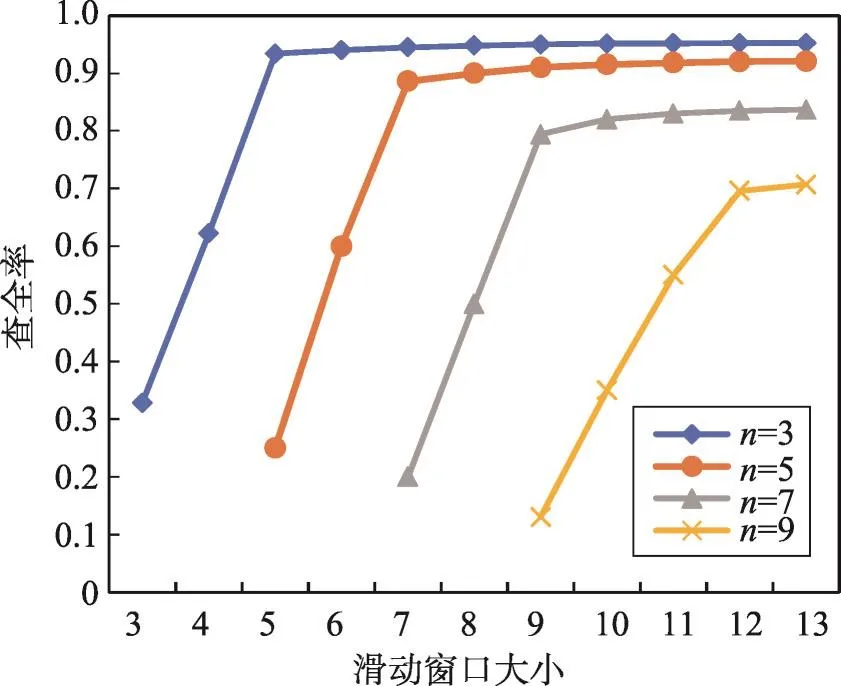
Fig.7 Relationship of recall and window size图7 查全率与窗口大小关系图
6.2 实验结果及分析
(1)基于滑动窗口的分块合并方法的作用
图8实验在数据方各自二次分块后,对比了简单合并和基于滑动窗口合并两种方法,简单合并为仅将不同数据方签名中LSH-key和suffix相同的分块合并。P1表示数据的扰乱比例为记录的30%,P2表示数据的扰乱比例为记录的75%,每个数据集的大小|Di|=20 000。图8(a)中,基于滑动窗口的分块合并方法查全率高于简单合并方法,尤其是数据扰乱比例大时,基于滑动窗口的分块合并方法具有容错性,因此显著优于简单合并方法。图8(b)中,基于滑动窗口合并方法查准率低于简单合并方法,因为其为保证容错率合并了更多分块。虽然基于滑动窗口的合并方法会导致需要匹配更多的候选记录组,但为避免数据扰乱造成的真实匹配记录组的过度损失,相较于简单合并方法,此方法更优,并且本文提出的高效的可伸缩匹配算法也可弥补此不足。
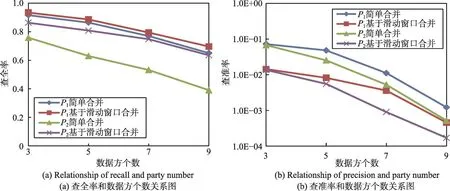
Fig.8 Comparison of common block merging and window-based block merging图8 简单分块合并与基于滑动窗口的分块合并对比
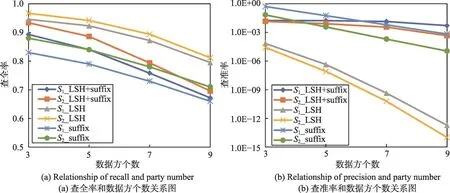
Fig.9 Comparison of double blocking,LSH and suffix blocking in different database sizes图9 不同大小数据集下二次分块、LSH和后缀分块对比
(2)分块方法查全率及查准率评估
图9和图10实验对不同大小和不同扰乱比例的数据集分别进行二次分块(结合基于滑动窗口的分块合并)、LSH分块和后缀分块,以数据方个数为自变量,查全率与查准率作为因变量,比较三种分块方法。
以往对分块方法查准率的评估均是在两方情景下进行的。文献[4]中两方Hamming-based LSH分块方法对每方大小为2.5×105的数据生成的候选记录对数量为5×107,推断其查准率必然低于0.005,扩展到多方时会生成更多的候选记录组,显著降低查准率。文献[2]中大小仅为5×103的数据集对应的查准率在0.2到0.6之间,当数据集规模增大时,查准率会持续降低。LSH方法简明的分块方式适合多方间的PPRL,但其查准率相较于其他分块方法较低。二次分块方法极大改善了LSH分块方法的查准率。

Fig.10 Comparison of double blocking,LSH and suffix blocking in different disturbances图10 不同扰乱比例下二次分块、LSH和后缀分块对比
图9中,S1表示每个数据方的数据集大小|Di|=10 000,S2表示|Di|=20 000,数据的扰乱比例均为30%。如图9(a)所示,三种方法均为S2比S1查全率高,因为数据集较大时分块内的记录较多,真实匹配的候选记录组损失的可能性就比较低,查全率由高至低分别是LSH分块方法、二次分块方法和后缀分块方法。随着数据方个数的增加,三种方法的查全率均有所下降,其中LSH方法下降最为缓慢,二次分块方法下降最为迅速。如图9(b)所示,三种方法均为数据集较大时查准率低,随着数据方个数的增加,LSH方法的查准率跨数量级迅速下降,二次分块方法和后缀分块方法的查准率缓慢下降,因为通过LSH方法形成的最终分块内记录数量明显多于其余两种方法。
图10中,P1表示数据的扰乱比例为记录的30%,P2表示数据的扰乱比例为记录的75%,每个数据集的大小|Di|=20 000,对两种扰乱比例下通过三种分块方法得到的查全率与查准率进行评估。如图10(a)所示,在数据方个数相同的情况下,数据的扰乱比例由30%增加到75%,二次分块方法和后缀分块方法的查全率比LSH方法降低明显,因为这两种方法的最终分块内记录数量少,数据扰乱比例高的时候更有可能损失真实匹配的记录组。图10(a)的其他情况与图9(a)一致。如图10(b)所示,扰乱比例的增加会造成分块方法查准率一定程度的下降,这是由于识别出的真实匹配候选记录组数量的减少造成的,其他情况与图9(b)基本一致。
上述实验表明,本文提出的二次分块方法查全率略低于LSH方法,查准率显著高于LSH方法,随着数据方个数的增加,LSH方法的查准率急剧下降,而二次分块方法的查准率下降趋势较为平缓,并且二次分块方法的查全率和查准率均优于后缀分块方法。实验结果说明,相较于LSH方法和后缀分块方法,本文提出的二次分块方法更适用于多方大数据集间的记录链接。
(3)多方可伸缩匹配算法精确性评估
图11实验采用P1=30%和P2=75%两种扰乱比例,表示同一实体的记录组数量为500的数据集。通过实验可以看出,错误率随数据扰乱比例值增加而升高。数据方个数增加时,错误率降低,匹配算法对候选记录组的判定更为精确。
(4)MP-SPPRL方法时间性能评估
图12中,实验测试了三种分块方法随数据方个数增加对应的第一阶段时间,每个数据集的大小|Di|=20 000,数据的扰乱比例为30%。可以看出相同数据方个数时应用LSH方法的时间明显高于应用二次分块和后缀分块两种方法的时间,且随数据方个数增加,应用LSH方法时间的增长速度快于应用其余两种方法。造成此情况的原因是,虽然LSH分块方法的操作更为快速,但其形成的分块内记录数量多,会导致生成大量候选记录组的时间花费大,生成候选记录组花费的时间同样是评价分块方法时间性能需考虑的因素。
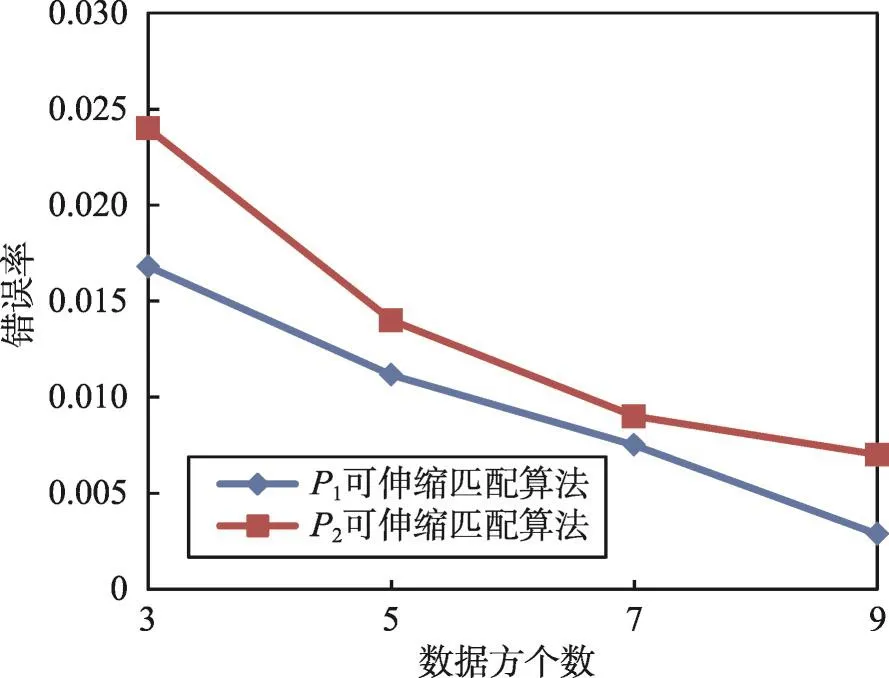
Fig.11 Error rate of scalable multi-party matching algorithm图11 可伸缩多方记录匹配算法错误率

Fig.12 Relationship of blocking runtime and party number图12 分块方法运行时间与数据方个数关系图

Fig.13 Relationship of matching runtime and data size图13 匹配算法运行时间与数据集大小关系图
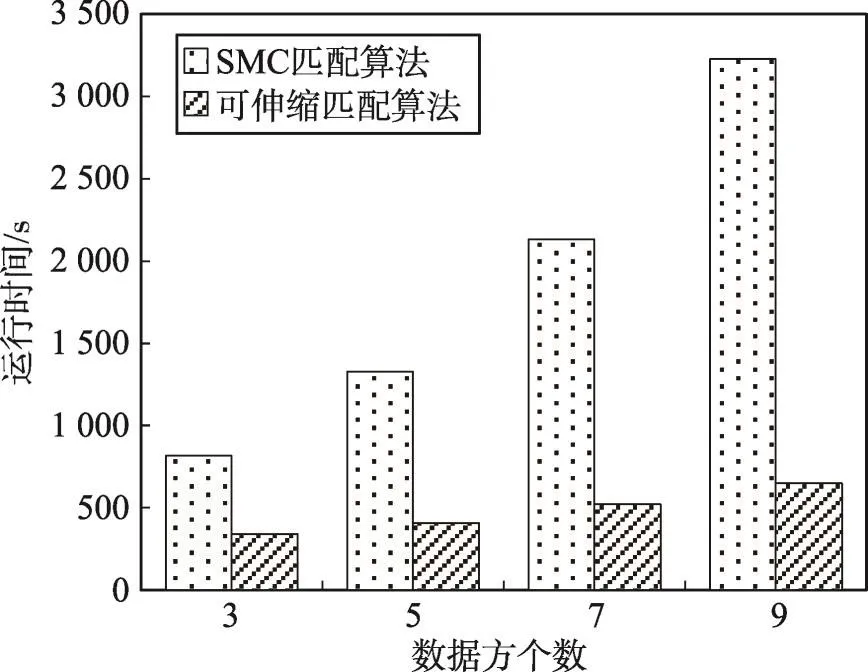
Fig.14 Relationship of matching runtime and party number图14 匹配算法运行时间与数据方个数关系图
在图13和图14实验中,数据的扰乱比例为30%,提前对数据集进行了二次分块及分块合并。图13实验表明了数据方个数n=3时,两种匹配算法的运行时间均随数据集大小的增加而升高,本文提出的可伸缩多方记录匹配算法所用时间约为SMC匹配算法时间的一半,可伸缩匹配算法在大小为1×105的大数据集下合理的运行时间说明了其具有良好的扩展性。图14实验表明了在|Di|=20 000数据集下,随着数据方个数的增加,两种匹配算法的运行时间都增加,但可伸缩多方记录匹配算法的时间增速明显小于SMC匹配算法,说明基于改进同态加密计算和提前终止匹配机制的可伸缩匹配算法在多个数据方的情况下表现突出。由图13和图14可以得出本文提出的可伸缩多方记录匹配算法在多方大数据集情景下具有高效性的结论。
7 结束语
本文提出了结合LSH分块和后缀分块的二次分块方法,在损失少量查全率的条件下大幅度提高查准率,同时具有高精确性与高效性。同时,将分块分散度度量引入二次分块,支持二次分块中两种分块方法的自调节,有效地控制查全率的损失。此外,基于滑动窗口的分块合并方法可以和二次分块方法结合,提高MP-SPPRL的容错率,避免真实匹配的候选记录组的损失。本文设计的基于SMC的可伸缩多方记录匹配算法能在保证强隐私性的前提下,明显缩减匹配时间,提高匹配效率,使其适用于大数据环境下。但是,随着数据方个数的增加,已有的PPRL方法和本文提出的MP-SPPRL方法的查全率均会下降,下一步,将试图在本文的基础上解决这一问题。
