基于改进EKF算法的航空锂电池SOC估算研究

王玲玲，周洁敏，郑 罡，朱悦铭

（南京航空航天大学，江苏 南京 211106）

0 引 言

多电飞机技术的应用形成了新型的飞机电气系统构架，促使电能取代部分机械能、液压能和气能成为机上主要的二次能源，飞机电源系统重要性达到了新的高度[1]。飞机电源系统中，蓄电池一般作为应急和辅助电源确保应急状态下的飞行安全，主要功能有：（1）在主发电机和应急发电机不能工作时，向维持飞行所必需的负载应急供电，如应急照明（由专用蓄电池供电）、无线电通信、应急仪表、应急电动机等；（2）作为飞机主发动机或辅助发动机的起动电源；（3）航前、航后时维护用的电源等[2]。荷电状态（State of Charge，SOC）是航空蓄电池监控系统中重要的状态指标。高精度SOC值可以为飞行员提供蓄电池可持续的供电时间、健康状况等状态信息，从而帮助飞机人员做出准备判断，以保证应急状态下的安全飞行和着陆。然而，航空蓄电池处于高空复杂多变的特殊环境，准确估计SOC值较为困难[3]。

目前，国内外进行SOC估算的研究方法主要有开路电压法、AH积分法和卡尔曼滤波法等[4]。由于环境温度和充放电电流等因素的影响，使用单一算法进行SOC估算存在一定局限性，如AH积分法的SOC初值及电流积累误差、开路电压法的不可在线测量、卡尔曼滤波法的近似线性估算误差等[5]。因此，本文将AH积分法和扩展卡尔曼滤波算法（Extended Kalman Filter，EKF）进行优势互补，考虑温度、电流等因素的作用，以实时性较强的改进AH积分法建立电池状态空间模型，然后使用EKF算法修正温度、电流等因素对SOC估算产生的影响。

1 改进的AH积分法

传统AH积分法中[6]，放电过程中t时刻的电池SOC为：

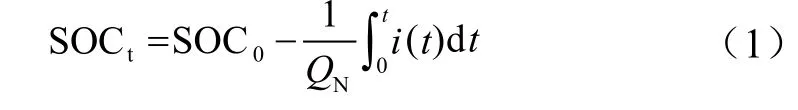
式中，SOC0是锂电池初始时刻的SOC，QN是电池额定容量，i(t)是充放电电流。

文献[7]通过实验研究了容量对SOC估算精度的影响。结果表明，锂电池容量随温度、电流因素的变化而变化，若不考虑温度、电流因素，会影响SOC估算精度。传统的AH积分法简单，能够较好地实现SOC估算，但是没有考虑温度、充放电效率因素对电池容量的影响。因此，本文对AH积分法进行修正，在电量计算过程中加入温度和充放电效率的补偿，使估算精度更高。

锂电池的充放电效率由Peukert等式得出，电池可用电量Q与放电电流I的关系为：

式中，A是与电池活性物质有关的常数；n是电池结构常数，一般取1.15～1.42。在初始条件相同的情况下，A和n的取值相同，因此可以得到充放电效率η：

式中，Ta是标准温度，T是当前温度。

分析可以得到修正的AH积分法为：

其中，Kt是温度影响系数，η是充放电效率系数。

2 锂电池等效电路模型建立

2.1 锂电池等效电路模型

Thevenin模型考虑了锂电池充/放电过程中内部出现的极化效应，精度较高，可以较精确地体现锂电池特性[8]。本文根据改进AH积分法，对Thevenin模型进行相应的优化改变，如图1所示。

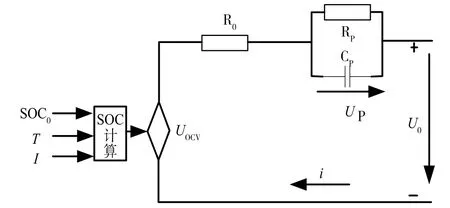
图1 改进型Thevenin模型

该模型考虑温度、电流因素的影响，加入SOC计算模块，采用改进AH积分法进行电池容量校正，更能精确地体现锂电池的动态特性。其中，UOCV为开路电压OCV，在一定温度下与锂电池SOC存在固定的对应关系；i为负载电流，充电时电流为负，放电时电流为正；R0为锂电池的欧姆内阻；RP、CP分别为锂电池的极化电阻和极化电容，主要用来表述锂电池内部的极化效应；UP为极化电容两端电压，U0为锂电池的输出电压。

根据基尔霍夫电压定律，可得：

2.2 模型参数辨识

2.2.1 OCV-SOC对应关系

为了获取锂电池OCV与SOC之间的关系函数，本文对型号为ICR18650-26F的钴酸锂电池进行实验研究。考虑温度的影响，在不同温度下，以0.2 C的放电率进行脉冲放电实验，在释放出10%容量后停止放电并静置1 h，在1 h末端锂电池电压几乎稳定不变，此时记SOC=0.9，然后进行下一轮放电。以0.1 SOC为步长进行循环放电，直至电池电压接近2.8 V时，停止放电。记录静置阶段结束时刻的端电压OCV和相应的SOC，采用MATLAB软件进行实验数据处理可以获得OCV-SOC的对应关系，如图2所示。

图2 不同温度下OCV-SOC对应关系

以25 ℃下SOC-OCV数据为例，如表1所示，利用MATLAB进行7阶拟合可得到拟合曲线，如图3所示。拟合公式如式（8）所示，其中和方差误差为0.003 679，均方根误差为0.022 93，拟合度达到99.83%。

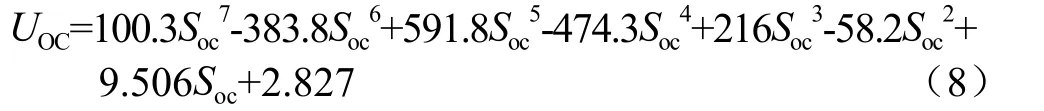
表1 OCV-SOC对应数据表

图3 OCV-SOC关系曲线

2.2.2 R0、RP和 CP参数辨识

模型参数R0、RP和CP不能直接测量，必须通过脉冲实验识别。图4显示了部分脉冲测试的端电压响应曲线。

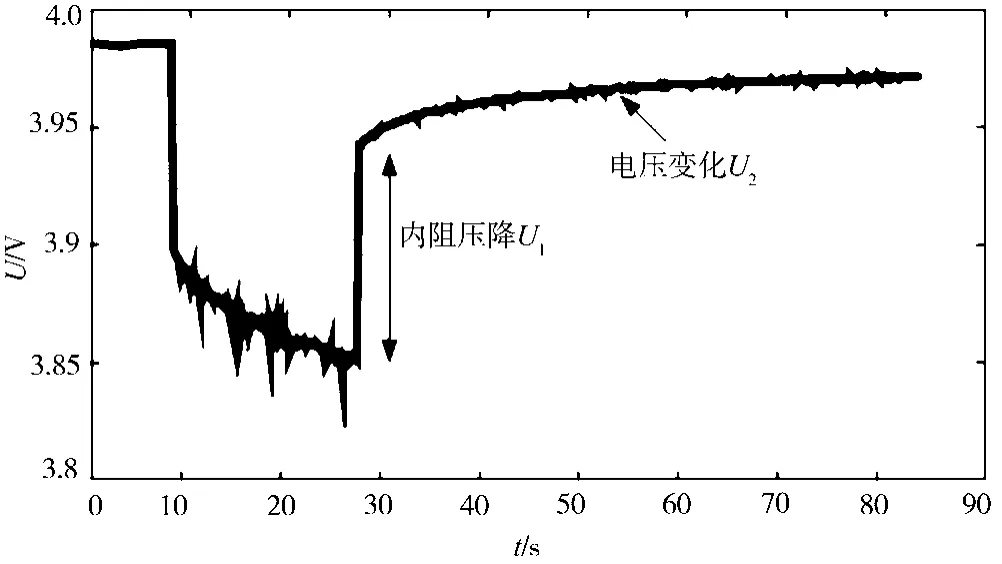
图4 脉冲放电时电压变化曲线

根据图4端电压响应曲线，加载和撤离电流瞬间引起的电压跃变是由电池内阻引起的。根据式（9），可以得到参数R0：

静置阶段，Thevenin模型电路处于零输入响应状态，此时的端电压满足：

其中UP=U2=IRP，UOCV为静置结束时的端电压，τ=RPCP为零输入响应时间。根据静置时端电压、时间等数据，采用MATLAB对式（10）的系数进行曲线拟合，可以取得参数τ，然后通过简单计算可以得到参数RP和CP，各参数辨识结果如图5～图7所示。

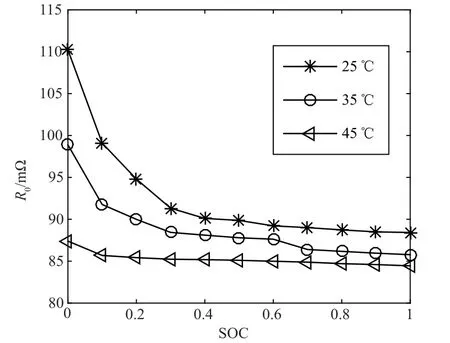
图5 R0辨识结果

图6 RP辨识结果

把辨识结果数值代入模型后进行验证，将仿真结果与试验结果进行比较，得到了很好的模拟效果，如图8所示。

2.2.3 充放电效率η和温度影响系数Kt

锂电池放电过程是一个复杂的电化学反应过程，表现出高度的非线性。它的SOC受多种因素的影响，除一些不能改变的因素，主要受电流和温度因素的影响[9]。改进的AH积分法加入了电流和温度补偿系数，可以修正电流、温度对电池容量的影响，减小SOC估算误差。

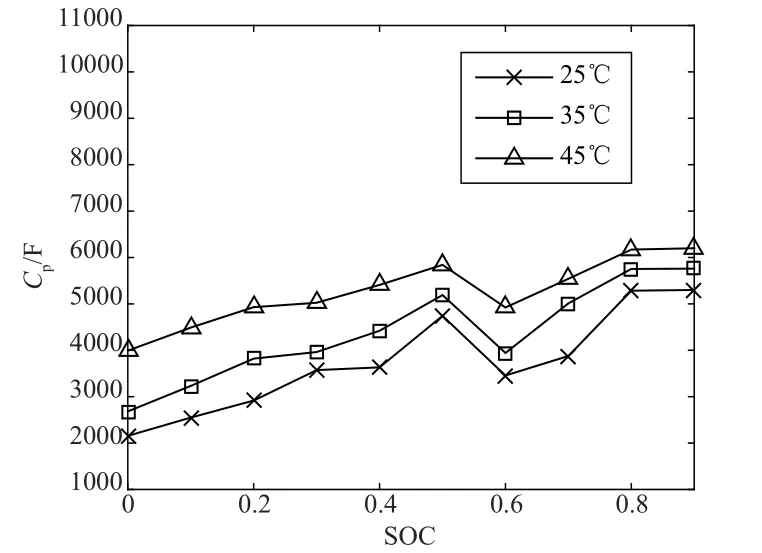
图7 CP辨识结果

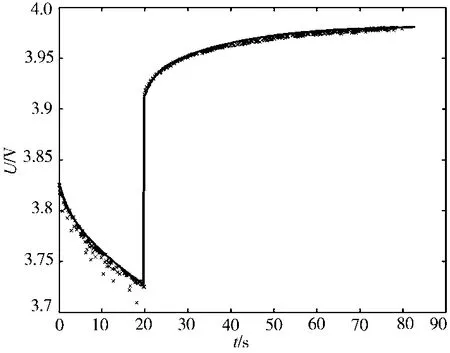
图8 电路模型仿真结果与试验数据比较

为了研究放电率和温度对锂电池容量的影响，对锂电池进行不同放电率、不同温度下的恒流放电实验，计算电池实际容量与放电率、温度的关系，并用最小二乘法拟合曲线，结果如图9和图10所示。

图9 锂电池实测容量和放电率关系图

实测容量Q与放电率x的关系式为：

实测容量QNT与温度T的关系式为：

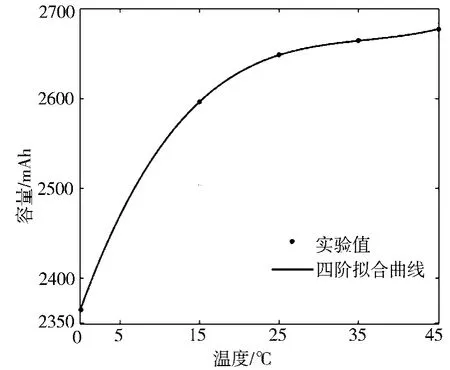
图10 锂电池实测容量和温度关系图

所以，温度影响系数Kt为：

3 基于EKF算法的锂电池SOC估计

卡尔曼滤波器主要用于估计线性时变模型，而锂电池是一个非线性系统，因此需要采用扩展卡尔曼滤波器EKF对锂电池状态空间模型进行处理，以提高锂电池SOC估计精度[10-13]。

EKF状态空间模型为：

式中，Ak、Bk、Ck+1和Dk+1分别为状态空间模型系数，Xk是状态向量，Yk是观测向量，Uk是控制向量，Wk、Hk+1分别是系统过程噪声和观测噪声。EKF算法的基本流程如式（16）～式（20）所示。

（1）时间更新

进行SOC估算前，需要得到锂电池状态空间模型，对AH积分法和电池电路方程进行离散化处理，得到：

式中，f(SOC)为锂电池OCV-SOC对应关系的拟合函数。

结合改进的AH积分法，本文选取SOC和电压UP作为状态变量，采用EKF算法进行线性化处理后，得到SOC估计的状态空间模型为：

式中，Δt是采样时间，QN是电池额定容量，ω1,k、ω2,k是系统噪声，υk+1是观测噪声。结合EKF状态空间模型，可以得到EKF所需要的矩阵：

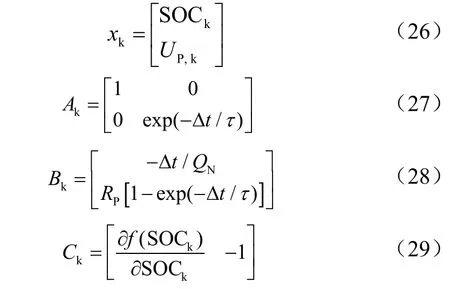
基于状态空间模型，结合EKF算法的递推流程式（16）～式（20），可以实现基于EKF算法的在线SOC估计。

综上所述，锂电池SOC的估算策略如图11所示。

图11 SOC估算策略

4 仿真建模及结果分析

为了验证基于改进AH积分法的EKF算法对SOC在线估计的准确性和鲁棒性，通过Matlab/simulink建模及软件编程实现SOC在线估计仿真，系统框图如图12所示，主要包括电流效率、容量校正、电池模型以及EKF算法模块等。

采用锂电池实验平台对ICR18650-26F锂电池进行实验研究，将实验获得的脉冲电流、端电压、环境温度等数据导入建立的模型中进行SOC估计的仿真验证，并根据仿真结果分析改进算法实现SOC估计的准确度。

图13是传统安时积分法、改进EKF算法与根据放电实验获取的SOC对比图，可以得出改进EKF算法估计SOC更加接近理论值，消除了传统AH积分法的初值误差和电流积累误差，在整个过程中收敛性更好。

图14是改进EKF算法进行SOC估计的误差曲线，可以看出整个过程误差较小，基本控制在2%以内，具有较高的估计精度。

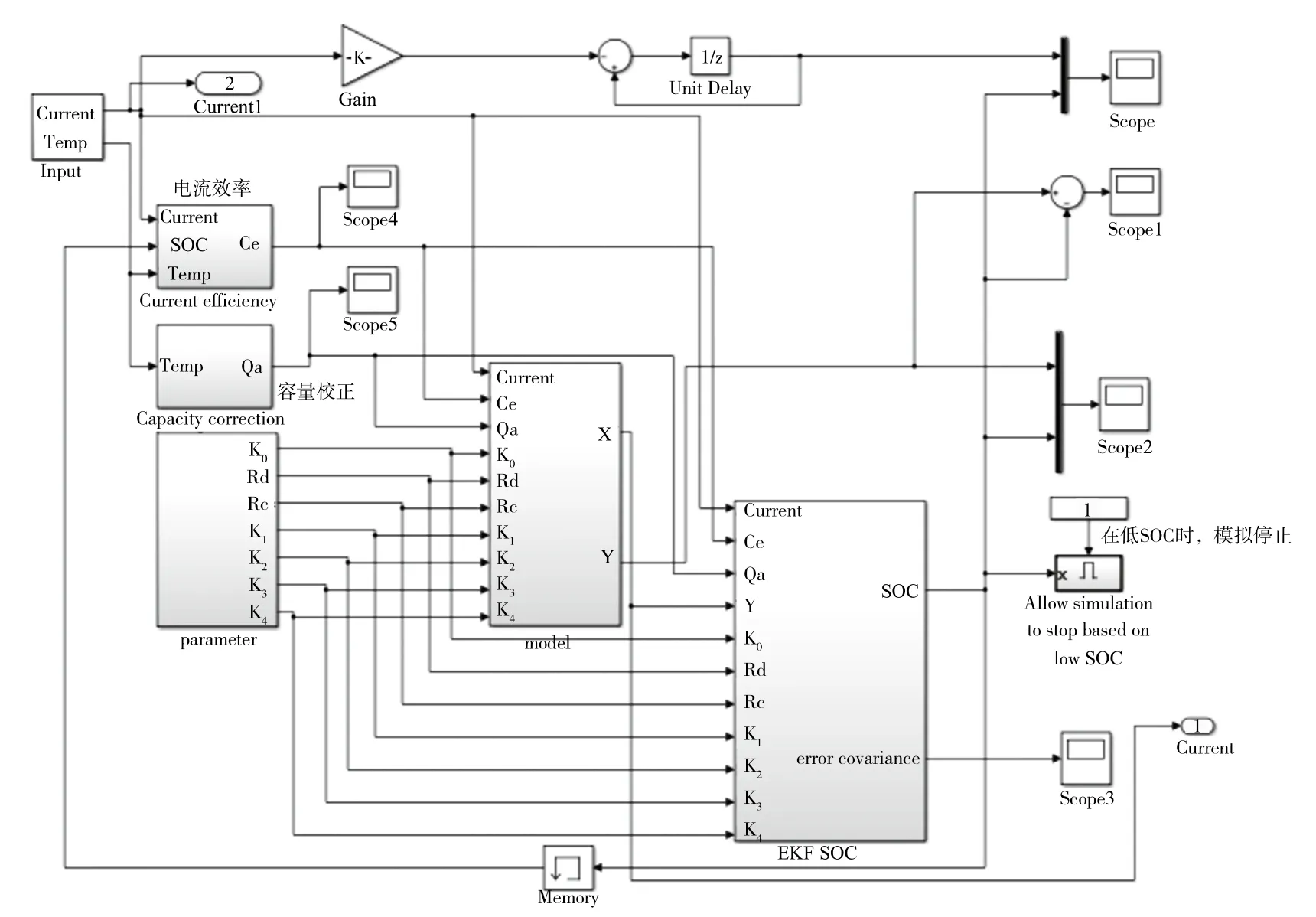
图12 扩展卡尔曼滤波系统框图

图13 SOC估计值与真实值对比

图14 改进EKF算法的SOC估计误差

5 结 论

（1）本文采用改进的电池模型，通过将改进的安时积分法、EKF算法相结合进行优势互补，实现了SOC的在线估算。仿真结果显示，该算法能较好地修正安时积分法的初值误差和电流积累误差。

（2）本文采用的算法相比于安时积分法，提高了估算精度，误差基本控制在2%以内。

（3）电池模型参数受多种因素影响，参数辨识的准确性会直接影响仿真精度。本文考虑温度、电流因素对锂电池SOC估计的影响，能较大程度地提高SOC估计精度。