低秩及几何约束的嵌入式阵列膛口波测向方法

王旭， 赵兆， 许志勇

(南京理工大学 电子工程与光电技术学院, 江苏 南京 210094)

0 引言

单兵便携式声探测系统、机器人、无人平台等现代侦察装备对小型麦克风阵列大气被动声探测系统的需求日益增长，相关功能涵盖对战场声源目标的检测、定位、识别等[1-3]。其中，便携式枪声探测系统因能快速捕获突发枪击事件并确定其射击点位置信息[4]，在近年国际反恐战争中战果显著，已被各国重视，具有重要的军事国防、公共安全价值。

弹头出膛时形成的膛口冲击波[5]是主要的枪声定位信息。在众多的麦克风阵列声源测向方法中[6-8]，基于阵元间波达时间差(TDOA)测量的最小二乘(LS)估计方法因实现复杂度低、环境适应性好等优点而广泛应用于包括枪声定位在内的各种实时声探测任务中[8-9]。然而，受外形结构、空间尺寸、使用运输等条件限制，便携式枪声探测系统所用的麦克风阵列通常采用嵌入式安装方式，导致部分阵元由于外壳遮挡而与目标处于非通视(NLOS)状态。考虑到远距离传播的枪声膛口波信号能量主要集中在数百赫兹的低频范围，NLOS阵元相关的实际TDOA主要受壳体衍射传播效应影响，不再与阵元间距和目标来向保持理想全通视条件下的理论对应关系，进而造成基于LS的膛口波方向估计结果出现明显偏差。

有关NLOS声源目标定位问题，许多文献主要关注声探测系统整体因障碍阻隔而无法直视目标时的解决方案[10-12]，一般不涉及壳体遮挡对嵌入式阵列目标方向估计的影响及其处理方法。而现有针对仅有部分NLOS阵元的研究通常采用球麦克风阵列声场模型来获得精确的声源目标方位估计[13]，但这种基于模型的衍射传播效应抑制方法一般较为复杂，难以实时实现；同时受成本、结构、使用方式等制约，便携式枪声探测系统通常阵元数很少，很难严格满足均匀球形阵列的模型要求，实践中也难以通过建模查表的方式来解决，而现有基于数据的方案虽然可以通过求解基于低秩和异常值个数约束的非凸优化问题有效校正阵元间TDOA测量噪声及个别异常值[14]，但却无法校正由于壳体遮挡衍射传播所造成的实际TDOA偏差，因为这种偏差既非测量误差也非异常值。

针对上述问题，本文以一种小型嵌入式四元平面麦克风阵列系统作为研究对象，通过在施加低秩约束的同时再增加几何约束，实现对实测TDOA矩阵中随机测量误差和壳体遮挡衍射传播偏差的联合抑制，同时选取距离目标最近的通视麦克风作为参考阵元，形成了一种新的枪声膛口波测向算法，明显减小了LS测向偏差的统计均值与方差。

1 问题描述

便携式枪声探测系统采用360°全方位远距离探测方式，目标通常远至数百米甚至上千米，相应的嵌入式四元平面麦克风阵列实物及其俯视二维测向示意图如图1所示。图1中S为远场目标，4个阵元M1、M2、M3、M4以嵌入式方式分别安装于扁平长方形壳体的4个侧面，顶端均与壳体侧面平齐。令阵列平面中心为本地坐标系原点O，各阵元的坐标向量分别为m1=[47 mm, 39.5 mm]T、m2=[34 mm, -52.5 mm]T、m3=[-47 mm, -39.5 mm]T、m4=[-34 mm, 52.5 mm]T。实际枪声探测任务中的目标俯仰角通常较小，以200 m外射击点目标为例，即使目标高度达到30 m(约10层楼高)，目标相对于阵列平面的俯仰角也仅为8.5°. 本文仅讨论枪声膛口波的方位角估计问题，较小的目标俯仰角对其方位角测量性能的影响可被忽略[9]。

由图1(b)可以看出，总是存在至少1个阵元与目标之间处于NLOS状态。考虑到远距离传播的膛口波能量主要集中在低频范围，NLOS阵元接收到的枪声信号主要是沿壳体衍射传播而来，传播延时增大，使得相关的实际TDOA偏离理想全通视直线传播模型下的理论值。以来自第二象限的远场目标为例，为尽量减小衍射传播效应的不利影响，可选择波达时间(TOA)最小的通视阵元M4作为参考麦克风，则在理想全通视条件下，目标方向对应的理想阵元间TDOA向量b应满足[8-9]：

(1)

式中：s=[sx,sy]T=[cosφcosθ, cosφsinθ]T为远场目标方向矢量，θ和φ分别为目标方位角(逆时针为正)和俯仰角(向上为正)；τij为阵列Mi和Mj之间的TDOA，i、j=1,2,3,4,i≠j；c为声速；A为阵列系数矩阵。

(1) 式所示的超定方程存在唯一的线性LS解为

s=A†b=(ATA)-1ATb=[x,y]T,

(2)

式中：A†为矩阵A的Moore-Penrose逆；x和y分别为cosφcosθ和cosφsinθ的估计，从而可得远场目标方位角的LS估计为

θ=arctan (y/x),

(3)

arctan(·)表示四象限反正切函数。

假设200 m处某个膛口波目标的方位角和俯仰角分别为120°和0°，结合4个阵元位置坐标可计算出理想全通视直线传播模型下各阵元的TOA理论值，进而可得以最小TOA阵元M4作为参考麦克风时的TDOA理想值向量b=[-0.151 0 ms, -0.364 3 ms, -0.213 4 ms]T，代入(2)式和(3)式可得目标方位角的LS估计为120.000 5°；即使目标距离近至本文验证试验所用的15 m，目标方位角的LS估计也为120.006 6°，估计误差仍可忽略。但实际阵元间TDOA因存在壳体遮挡引起的衍射传播延时而将大于相应的理想值，再加上不可避免的随机测量噪声和异常值等实际因素，基于理想全通视模型的目标方位角LS估计结果将出现明显偏差。例如前期试验中在120°方位角处的5次TDOA实测值对应的目标方位角估计分别为125.59°、127.07°、125.45°、130.47°、126.73°，误差高达5.45°～10.47°. 更为棘手的是，这种测向误差是随目标来向和环境因素的不同而变化，造成在目标位置未知的实际应用条件下，壳体遮挡衍射传播效应引起的测向误差方向和误差程度都难以实时预测，因而枪声探测系统的膛口波测向性能必须根据实际测量数据进行校正。

2 TDOA矩阵校正

考虑到枪声探测系统采用的麦克风阵列形状和阵元位置信息均为已知的先验知识且通常固定不变，本文以图1所示的四元嵌入式平面麦克风阵列为例，提出一种TDOA矩阵校正方法，通过同时施加低秩及几何约束分别抑制TDOA测量值中的随机测量噪声和衍射传播影响，从而明显减小嵌入式平面阵列的膛口波测向偏差。

令远场目标信号传播至阵元Mi的波达时间为ti，i=1,2,3,4. 定义阵列的TOA向量为x=[t1,t2,t3,t4]T，以及阵元Mi和Mj之间的τij=ti-tj，i、j=1,2,3,4,i≠j，结合全1向量1=[1, 1, 1, 1]T可得相应的反对称TDOA矩阵

M=x1T-1xT.

(4)

显然，(1)式中TDOA向量b的所有信息均已包含在矩阵M中。当同时存在TDOA测量噪声以及少量异常值(含丢失值赋值)时，实测TDOA矩阵可表示为

=M+N+S,

(5)

式中：N为反对称的测量噪声矩阵；S为TDOA矩阵中的加性异常值。对于俯仰角较小的远场目标，(4)式所示理想全通视TDOA矩阵M的秩为2，不会出现所有阵元与目标距离相同的平凡解情况(此时M为全零矩阵)。基于这一事实，文献[14]采用低秩和异常值个数约束将(5)式中对矩阵M的估计任务转化为一种非凸优化问题并求解。值得注意的是，文献[14]中方法有效的前提是存在一个隐含假设，就是(5)式右式中的M+S不能分解为(4)式所示形式，即不存在一种实际阵列构型，它的无噪TOA向量x能通过(4)式得到秩2的反对称矩阵M+S.

然而对于嵌入式平面阵列，当部分NLOS阵元受壳体遮挡衍射传播效应影响时，情况将与之不同。若不考虑其他任何TDOA异常值和随机测量误差，实际的无噪TDOA矩阵仍然可以表示为M+S形式，但此时的M和S将分别由理想全通视TDOA值和衍射传播TDOA偏差构成。由于嵌入式阵列中NLOS阵元因其对应的实际TOA大于理想全通视情况而可等效于阵列形状发生了改变，此时(5)式中的M+S将与受衍射传播影响的实际无噪TOA向量对应，即无论是M和S本身还是M+S作为一个整体，都可以分解为(4)式所示的反对称秩2矩阵构成方式。由于衍射传播TDOA偏差矩阵S还随目标来向变化且难以实时预测，因此仅采用秩2约束无法分辨M和S，使得文献[14]所提方法因其隐含假设不再成立而无法准确重构理想全通视TDOA矩阵M，即不能校正衍射传播引起的TDOA偏差。

为了同时抑制TDOA实际测量值中的随机测量噪声与衍射传播偏差，本文在现有低秩约束基础上又施加了对应阵列形状特征的几何约束，即将(5)式中对理想全通视TDOA矩阵M的估计任务转化为如下有约束凸优化问题：

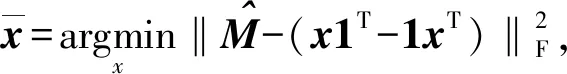
(6)

式中：‖·‖F为Frobenius范数；约束矩阵D=[1,c]，c为几何约束向量，包括1Tx=0和cTx=0两部分，前者与理想全通视TDOA矩阵M应为秩2的低秩要求密切相关，用于抑制高斯随机测量噪声[14]，后者则体现了图1所示平行四边形麦克风阵列所对应的形状特征几何约束。由于τ12=τ43，因而(6)式中

c=[1, -1, 1, -1]T.

(7)

针对(6)式应用Lagrange乘数法构造函数

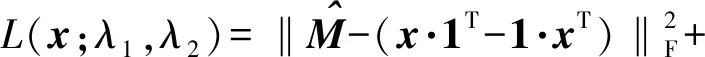
(8)

式中：λ1、λ2为拉格朗日乘子。

考虑到

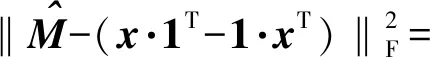
则令(8)式分别对x、λ1、λ2的1阶导数为0，可得

(9)

(10)

最后可得校正后的理想全通视TDOA矩阵估计为

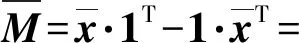
(11)

3 嵌入式平面阵膛口波测向方法

本文提出的嵌入式平面阵膛口波测向算法主要包括3个主要步骤：参考麦克风选取、TDOA矩阵校正、LS方位角估计。

首先，考虑到与目标距离最小的阵元处于通视状态，选择该阵元作为参考麦克风有利于减小(1)式中TDOA向量b受壳体遮挡衍射传播效应的影响程度，从而为降低LS方位角估计偏差提供良好基础。由(4)式可知，TDOA矩阵M中每一列都是TOA向量x加上不同的时间参考点，因而理论上每一列中与最近通视阵元序号对应的元素均应在该列中数值最小，即TOA最短。但需要强调的是，由于TDOA估计过程中不可避免地会存在测量噪声甚至出现个别异常值，实测TDOA矩阵中每列各元素之间的大小关系有可能发生偶然随机变化。因此采用多数表决方式确定参考麦克风序号，即首先记录实测TDOA矩阵中每列最小值所在的行序号，然后以最小值出现记录最多的行序号作为距离目标最近的通视阵元序号，并选取该阵元作为参考麦克风。

需要说明的是，通过改变各矩阵或向量的维数以及几何约束的表现形式，上述膛口波测向算法就可直接推广到阵元数量或阵列形状各不相同的其他嵌入式麦克风阵列系统。

4 试验验证

验证试验在较空旷的室外环境进行，试验布设示意图及试验现场照片如图2所示。图2中的嵌入式四元平面麦克风阵列系统被水平固定在三脚架上，以阵列中心为坐标原点，通过水平顺时针旋转阵列系统来等效从小到大地改变目标方位角。作为模拟射击点目标的扬声器与阵列高度基本相同，放置在距离阵列中心15 m处，该距离远大于阵列孔径，因而可模拟远场情况。试验中，目标方位角从0°开始以30°步进递增变化一周，在每个目标方位角位置进行26次独立试验，12个方位角位置共计进行312次独立试验。每次试验中扬声器播放一段含有外场实测的枪声膛口波信号录音。

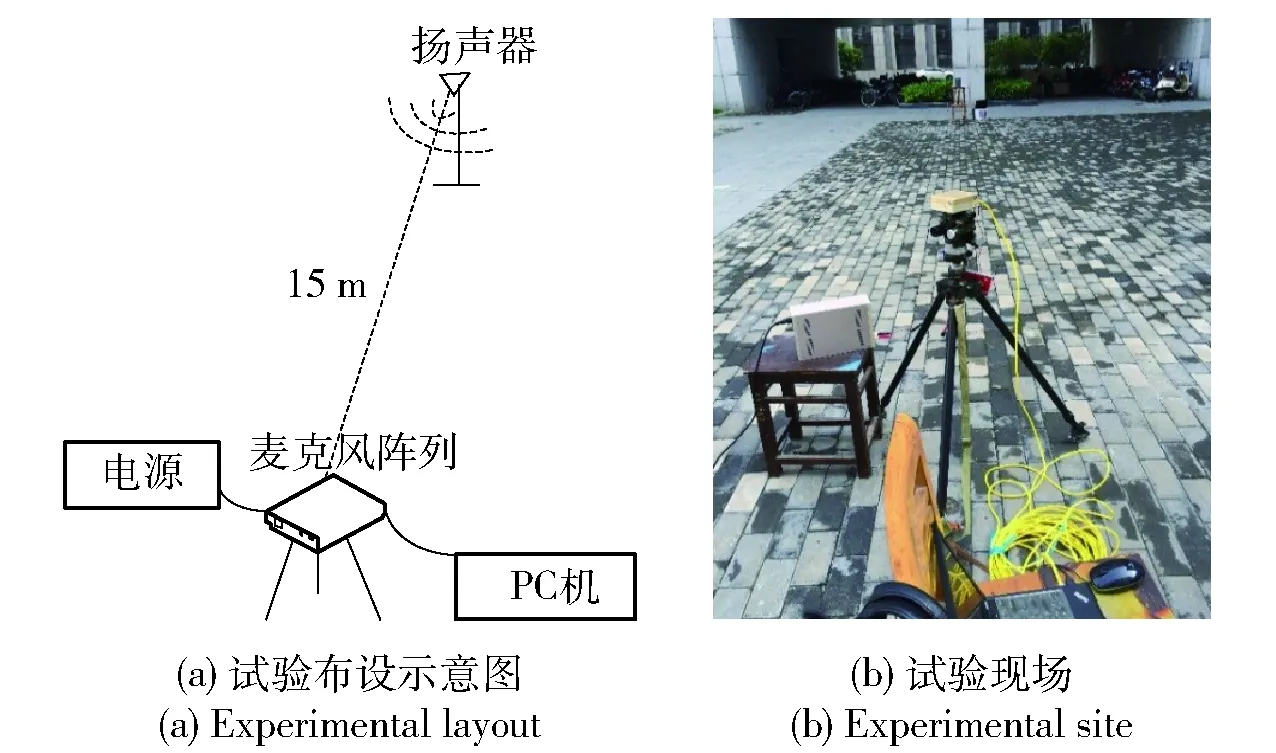
图2 试验布设示意图及试验现场Fig.2 Experimental layout and experimental site

采用理想全通视直线传播模型下基于TDOA的常规LS测向算法(下文简称常规方法)作为性能对比，并定义测向误差为目标方位角估计值与真实值之差。

图3给出了本文方法和常规方法在12个测试方位角上各26次独立试验的测向误差分布。图3中，常规方法的测角误差在一些方位角处散布较大，而经过本文方法校正后，各方位角的测向误差分布则已趋向集中。

图3 本文方法和常规方法的测向误差分布Fig.3 Distribution of azimuth estimation errors of the proposed and conventional methods

图4比较了两种方法的测向误差总体分布直方图。对比图4(a)、图4(b)可以看出，常规方法的测向误差主要集中分布在-2.03°～5.14°范围内(上下四分位数误差范围)，分布均匀程度较高，且误差绝对值的最大值高达23°. 而本文方法测向误差则主要集中分布在-1.38°～2.84°范围内(上下四分位数误差范围)，相应频度随着误差绝对值增大而很快下降，误差绝对值的最大值也降为10°.

图4 本文方法和常规方法的测向误差分布直方图Fig.4 Histograms of azimuth estimation errors of the proposed and conventional methods

图4中，常规方法和本文方法的测向误差统计均值正负标准差分别为1.73°±5.87°和0.90°±3.55°，统计中值分别为1.88°和0.87°. 实际目标方位角通常未知且随机，通常假设实际目标方位角在0°～360°之间均匀分布。为使全方位的总体测角性能相对均衡，同时考虑到两种方法测向误差的统计均值与统计中值基本相等，实际应用时可预先补偿上述统计均值。两种方法在均值补偿后的测向误差绝对值所对应的累积概率分布对比如图5所示。需要强调的是，就枪声探测系统实战环境下的技术指标而言，当前以英国Ears SWATS II代、美国Boomerang Warrior-X系统为代表，这些国外同类便携式产品的枪声膛口波测向性能通常以±7.5°为测向精度考核标准[4]。通过考察图5可知：针对测向误差绝对值在7.5°以内的累积概率，常规方法仅为0.86；而本文方法达到0.94，测向性能明显提升。

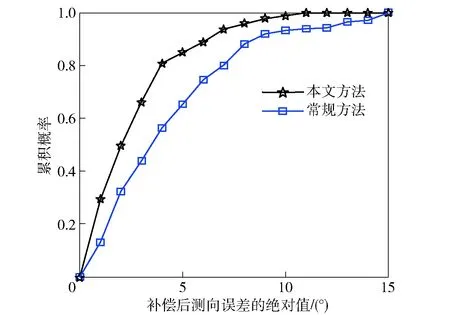
图5 均值补偿后两种方法的绝对测向误差累积概率分布Fig.5 Cumulative probability distributions of absolute azimuth estimation errors after mean value compensation

5 结论

对于小型嵌入式平面阵枪声探测系统，部分阵元将因壳体遮挡而不能直视目标。低频能量集中的枪声膛口波信号传播至NLOS阵元会因衍射传播而出现额外延时，导致实际阵元间TDOA不再满足与阵元间距和目标方向之间的理论函数关系，使得基于理想全通视直线传播模型的常规LS测向结果发生较大误差，该误差在实际中很难预测和建模。通过在低秩约束的基础上增加阵列形状几何约束来构建凸优化问题，同时选取距离目标最近的通视麦克风作为参考阵元，能够有效抑制TDOA随机测量噪声与壳体遮挡衍射传播效应，明显提高基于TDOA的LS测向精度。试验结果表明，所提方法的膛口波测向误差绝对值在7.5°以内的累积概率由常规方法的0.86提升至0.94，误差分布也更为聚集，能够满足实际便携式枪声探测系统的测向指标要求。