基于悬吊法的汽车发动机惯性参数测试分析

廖美颖， 王小莉， 李利平， 梁广源

(1.广州汽车集团股份有限公司 汽车工程研究院， 广州 511434； 2.广东技术师范大学 汽车与交通工程学院， 广州 510665； 3.华南理工大学 机械与汽车工程学院， 广州 510640)

准确获取发动机惯性参数是汽车发动机系统设计与优化的重要前提之一。发动机的惯性参数包括：质量、质心位置以及在一个坐标系下的转动惯量和惯性积。基于悬吊法的三线扭摆系统通过引入万向节连接装置，当万向节的一端连接形状复杂的物体时，物体质心自然落在扭摆轴线上[1]。但是，在实际测试过程中会频繁出现测试误差偏大甚至错误的问题[2]。本文基于开发中的三线扭摆的惯性参数测试试验台，在阐述基本测试原理的基础上，分析汽车发动机惯性参数测量时的测试方法、数据处理方法和误差分析方法，以及某具体型号发动机惯性参数的测试流程和测试精度分析。

1 惯性参数测试及计算原理

1.1 悬吊法测试原理

基于悬吊法惯性参数测试系统[1]如图1所示，包括扭摆圆盘、十字轴万向节、摆线、摆臂、平衡调整块、万向节连接套筒等。其中3个摆臂为等圆周分布，以确保扭摆装置处于水平状态。

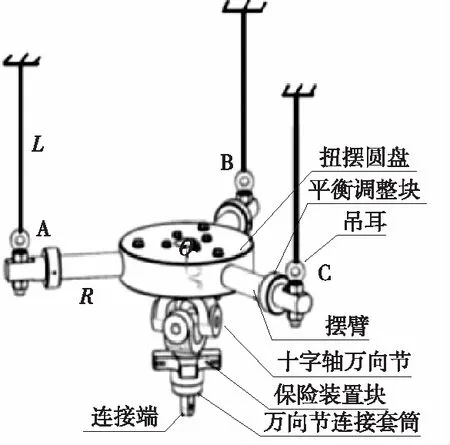
图1 悬吊法扭摆测试系统

当给定三线扭摆系统某一小角度(3°～5°)的初始角位移，被测刚体的转动惯量Jc为[3]：

(1)

式中：R为扭摆半径；L为摆长，穿在吊耳上；m为被测刚体的质量；m0为空摆质量；Ts为系统扭摆周期；T0为空摆扭摆周期。

1.2 坐标系及转换原理

悬吊法在解决传统三线扭摆法多种姿态调整弊端的同时，需要对直接测量点的坐标进行不同坐标系之间的变换，进而计算刚体惯性参数[4]。

1) 参考坐标系：用于描述刚体质心位置坐标系，如图2所示。

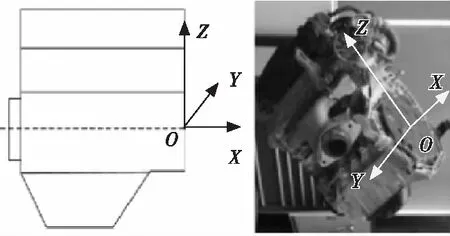
图2 发动机参考坐标系

2) 质心坐标系：用于描述刚体的惯性参数的坐标系。以刚体的质心为原点，坐标轴的方向平行于参考坐标系的坐标轴。

3) 摆盘坐标系：用于描述扭摆轴线方位，以下圆盘中心点O1为原点，摆盘坐标系的Z1轴刚好为扭摆轴线X1轴在下圆盘平面内，远离圆心方向为正；Y1轴由右手定则确定。

坐标转换法适用于点或者矢量在两坐标系中的转换。某点k在不同参考系下坐标之间存在以下关系[4]：

(2)

式中:α1、β1和γ1分别为O2X2与O1-X1Y1Z1的坐标轴的夹角；α2、β2和γ2分别为O2Y2与O1-X1Y1Z1的坐标轴的夹角；α3、β3和γ3分别为O2Z2与O1-X1Y1Z1坐标轴的夹角。

1.3 质心计算原理

由于重力的作用，被测刚体的质心是落在扭摆轴线上的。一般以刚体两种不同姿态下的扭摆轴线之间的公垂线中点表示质心[1]，为精确测出质心位置，需要测出多种不同姿态下的扭摆轴线。计算过程中，以第1、2组求解一个质心，第3、4组求解一个质心，最后通过最小二乘原理拟合出质心位置，质心具体计算原理见参考文献[1]。

根据1.2节对坐标系的定义可知，基于三坐标仪确定的扭摆轴线是定义在摆盘坐标系中的，但是发动机质心坐标要求定义在参考坐标系中。因此，需要将摆盘坐标系中定义的质心坐标转换到参考坐标系中。

1.4 转动惯量和惯性积计算原理

根据刚体转动惯量的转轴定理[1]，被测刚体对扭摆轴线的转动惯量Jc与对刚体质心坐标系的惯性参数(Jx、Jy、Jz、Jxy、Jyz和Jzx)之间存在以下关系：

Jc=Jxcos2α-2Jxycosα·cosβ+Jycos2β- 2Jyzcosβ·cosγ+Jzcos2γ-2Jzxcosγ·cosα

(3)

其中α、β和γ分别为扭摆轴线与刚体质心坐标系三坐标轴的夹角。要计算出被测刚体在质心坐标系下的惯性参数，则至少要测出6组不同姿态下被测刚体绕扭摆轴线的转动惯量及其扭摆轴线与质心坐标系的方位角。对于实测多种不同姿态的同一被测刚体而言，式(3)可扩展成下列矩阵形式：

Jc=AJ

(4)

被测刚体在质心坐标系下的惯性参数矩阵：

J=(ATA)-1ATJc

(5)

根据经验，应测10～12组数据较为合适[4]。

2 测试误差分析及精度确定

基于悬吊法的惯性参数测试，误差主要有：系统误差和过失误差[2]。系统误差包括：试验台的加工误差、坐标的测量误差、周期测量误差以及三线扭摆装置的质量、扭摆长度和半径等的测量误差；过失误差包括：设备使用不规范产生的误差，如扭摆角度较大等。为提高测试精度，系统误差可采取有效措施来减小，过失误差可通过数据处理的方法来避免。

2.1 系统误差分析

为了减小系统误差，应提高试验台的加工精度；采用高精度三坐标测量点的坐标；使用高精度光电传感器测量扭摆周期。同时，还需要进行试验台的参数标定，以消除三线扭摆装置的质量及扭摆长度的测量误差[5]。

理论上，悬吊法三线摆的摆线是无质量、无弹性、无阻尼的线[1]。根据试验台的设计情况，金属线的质量对空摆质量有一定贡献。扭摆装置安装后，扭摆长度L难以直接测出。将2个大小不同的标准圆柱块(图3所示)悬吊在万向节连接套筒上，对空摆质量和扭摆长度L进行标定。标准块1直径为200 mm，高为80 mm，质量为19.39 kg；标准块2直径为300 mm，高为70 mm，质量为38.48 kg。

(a) 标准块1

(b) 标准块2

由式(1)可知，对于标准块1：

(6)

对于标准块2：

(7)

上式中，2个标准块的质量M1和M2可通过电子秤测量得到；2个标准块绕轴线的转动惯量J1和J2可根据理论力学计算得到；扭摆周期T1和T2通过光电传感器测出；扭摆半径R可通过测出两摆线的距离再根据几何关系计算得到，如图1所示。因此，通过求解方程组可得到标定的空摆质量M0和扭摆长度L。标定结果如下：空摆质量M0=51.05 kg，扭摆长度L=3 163.56 mm。

为检验标定后试验台测试转动惯量的精度，将2个标准块用双头螺栓串联成标准检验块，将转动惯量的实测值与数模理论值进行比较，确定转动惯量的测试精度。标准检验块的质量为57.87 kg，测得其扭摆周期为1.383 2 s，转动惯量为0.534 4 kg·m2，与理论计算值0.530 9 kg·m2比较，相对误差0.664 6%，小于1%。经过标定后的试验台测试转动惯量的精度较高。

2.2 过失误差分析

为了减小过失误差，可通过数据处理的方法来避免。对于已经测量的10～12组数据，若数据中存在相对误差偏大的数据，可采取剔除的方式来处理。为此，专门编制了数据处理软件，方便对已测量的数据进行数据处理，避免过失误差对试验精度的影响。

2.3 测试精度的确定

根据误差传递规律[6-10]，结合试验台的结构和测试原理，试验台测试相对误差主要由以下几部分组成[1]：

(8)

由于空摆质量M0和扭摆长度L已经标定过，因此等号右边前两项相对误差可忽略不计，其余各项的误差最大值为：

|ΔR/R|=0.2%，|ΔT/T|=0.3%

则转动惯量测试的相对误差ΔJ/J≤1%。

为了确定该试验台的测试精度，实测某标准测试件(由尺寸分别为120 mm×150 mm×175 mm，230 mm×260 mm×160 mm的2块长方体焊接而成，如图4所示)的惯性参数，再与理论值作对比。根据工程经验，一般情况下，质心坐标的识别精度用绝对偏差描述，以小于±1 mm为宜；惯性矩阵的识别精度可用多方位的转动惯量相对误差描述，以约为1%为宜[4]。

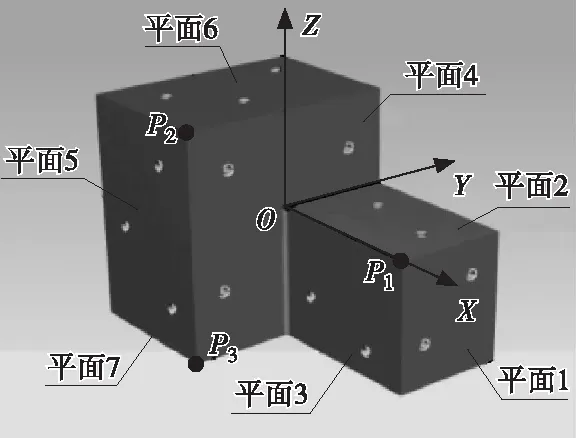
图4 长方体组合标准测试件

实测标准测试件11种不同姿态下绕扭摆轴线的扭摆周期，以及在摆盘坐标系下确定姿态坐标系的固定点(P1、P2和P3)坐标值，基于直接测量的扭摆周期和不同姿态下标准测试件绕扭摆轴线的转动惯量，部分数据如表1所示。

利用表1中的11组测试数据拟合出的质心坐标值见表2。由表2可知，11组数据拟合出的质心测试值与理论值之间误差较大(>1 mm)，由表1测试转动惯量和转动惯量的拟合值数值对比可知，第3、4和9组转动惯量测试值与拟合值的相对误差绝对值大于1%。经现场分析发现，第3、4和9组的悬吊点位置选择不合理。因此，剔除后再进行一次拟合，拟合的转动惯量见表1所示。利用有效的8组数据计算质心坐标见表2。从表2可知，剔除第3、4、9组数据后，质心测试值与理论值之间的误差小于1 mm，符合测试要求。

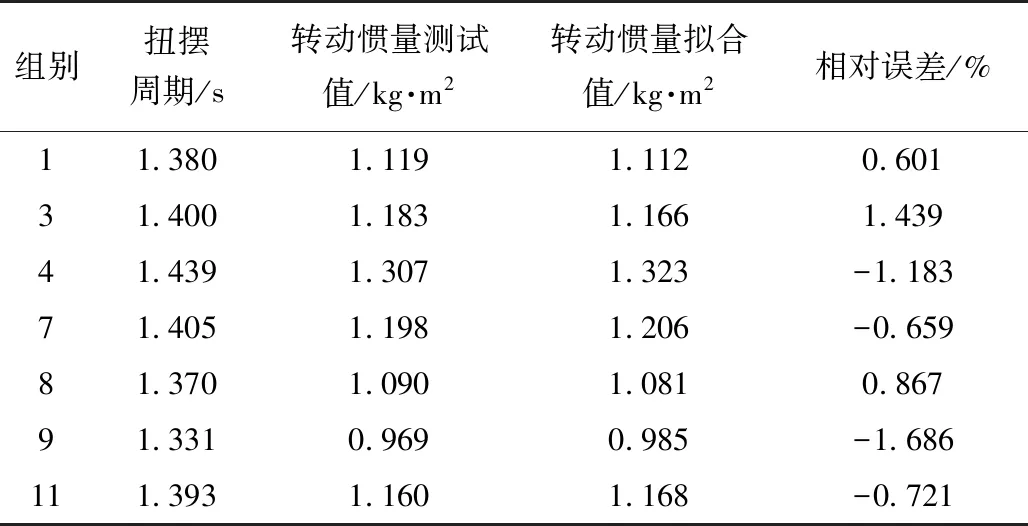
表1 扭摆周期和转动惯量实测数据

表2 剔除前/后标准测试件质心坐标测试值 mm

利用有效的8组测试数据，基于式(7)可计算出标准测试件在质心坐标系下的惯性参数，转动惯量测试值与理论值进行比较，相对误差均<1%。结果表明，该惯性参数测试试验台测试精度较高，测试方法有效，无需对试验台进行校正处理，能用于实测汽车发动机惯性参数。

3 某发动机惯性参数的实测及误差分析

以某汽车发动机为测试对象，探究其惯性参数的测试方法。该汽车发动机的质量经电子秤称量为83.8 kg。根据机体的实际情况，选择10个吊装用螺纹孔，用于10种不同的悬吊姿态。在发动机上非共线的3个螺纹孔上安装加工精度较高的轻质球头螺栓，取这3个球头的圆心作为确定发动机姿态坐标系的3个固定点(P1、P2和P3)。测试流程如下：

1) 建立发动机参考坐标系与姿态坐标系坐标转换关系：用三坐标测量仪建立发动机参考坐标系，建立方法见1.2中1)；以发动机参考坐标系为基准，测出确定姿态坐标系的固定点(P1、P2和P3)的坐标值。

2) 选择合适的悬吊点，将发动机与三线扭摆装置通过专用夹具连接安装，测出该姿态下的扭摆周期。

3) 用固定支架固定发动机。

4) 基于三坐标测量仪和摆盘坐标系的定义，建立摆盘坐标系。

5) 在摆盘坐标系下测出确定姿态坐标系的固定点(P1、P2和P3)的坐标值。

6) 重复步骤(2)(3)和(5)，按照悬吊点的顺序，测出10种不同姿态下发动机的扭摆周期和在摆盘坐标系下对应的确定姿态坐标系的固定点(P1、P2和P3)的坐标值。

7) 将上述测试数据，代入相应的计算公式，得出利用试验台测试的发动机惯性参数，部分见表3。

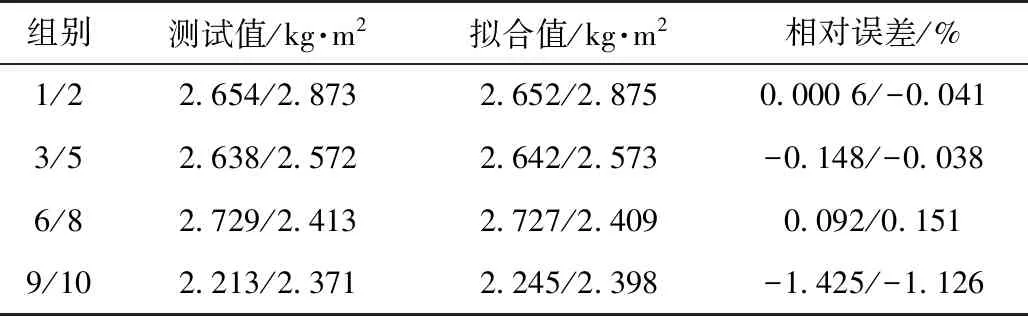
表3 转动惯量测试值和拟合值

测出10种不同姿态下发动机的扭摆周期和球头螺栓对应的3个球心点坐标，基于此直接测量数据计算出发动机的转动惯量，第9组和第10组测试转动惯量与拟合的转动惯量的相对误差均>1%。剔除后再对惯性参数进行计算，最终获得基于试验台测试得到的发动机惯性参数，见表4。

表4 某发动机惯性参数的测试值

4 结束语

本文阐述了悬吊法惯性参数测试试验台的测试原理，探究了试验台测试流程、数据分析方法及误差分析方法。分析了试验误差来源，并对试验误差的减小方法进行了阐述，结果表明该试验台的测试精度符合工程实际要求。最后实测某汽车发动机的惯性参数，验证了该测试方法的可行性与可重复性。