刘徽和祖冲之曾计算圆周率的近似值吗?
2019-04-16鞠实儿张一杰
鞠实儿 张一杰
(中山大学逻辑与认知研究所,广州 510275)
1 问题与方法
1.1 周径率是圆周率π吗?
明末西学东渐,西方数学开始传入中国。万历三十五年(1607),徐光启和利玛窦完成Elements(《几何原本》)前六卷的翻译,在数学领域实施中西会通。([1],页374)其中:徐利二人将几何中的“Circulus”翻译为中国算学(以下简称:中算)中的“圆”([2],页31)。根据这一翻译,中算本土概念“圆”被等同于欧氏几何之“Circulus”(1)在没有特别指明的情况下,本文用“欧氏几何”指在起源于欧几里得《几何原本》,在近现代已经成熟的欧氏平面几何。此处“Circulus”与后文“Circle”的所指为同一对象,即欧氏几何中的圆。。这一事件使得作为圆周率π概念之基础的几何对象Circulus被引入到中国传统语境中,两者被等价。康熙五十二年(1713),康熙皇帝下令御制之《数理精蕴》,于六十一年(1722)铜活字印刷。([3],页613—620,641—643,647—674)此书体现了康熙帝所倡“西学中源”说:“有汤若望、南怀仁、安多、闵明我,相继治理历法,间明算学。而度数之理,渐加详备。然询其所自,皆云本中土所流传。”([4],页3—16;[5])把西方传教士传入的历法算学说成“中土流传”,又云“其圆方矩度之规,推测分合之用,莫不与西法相为表里。……以明数学之宗,使学者知中外本无二理焉尔。”(2)康熙学自传教士、最终修订入《数理精蕴》之7卷本《几何原本》,并非徐利二人译本,属于另一版本链,见[6][7]。亦参见[3],页613—620,641—643,647—674。乾隆年间,《四库全书》收录之《数理精蕴》提要云:“径一者,周三一四一五九二六五,泰西法亦同其率”(3)见[8],页799。原文为“六二五”,下划线为笔者所加。耐人寻味的是,此处对率的表述在论断“泰西亦同”的同时,仍保留中算传统的一组率数的形式。;通过皇权,以官方经典的方式确立:中国古算中周径相与之率(本文简称:周径率)就是欧氏几何中的圆周率π(4)周径相与之率,即魏晋数学家刘徽《九章筭术》的注解中对古算圆周与径的关系的描述。。
进一步,近现代学者在介绍中国的数学成果时,往往也把周径率翻译为圆周率π。咸丰二年(1852),传教士伟烈亚力(Alexander Wylie,1815—1887)以欧氏几何中的“circle”和“ratio”(“比率”)来描述刘徽和祖冲之的计算成果;同时,最先以圆周率的形式向西方介绍了中算家刘徽(活跃于263)和祖冲之(429—500)(简称刘祖)在周径率计算方面的成果([9],页170—171)。1913年,数学史家三上义夫(Mikami Yoshio)发表了数学史专著《中日数学发展史》。在此书中,他亦将中算的周径率等同于欧氏几何中圆周率,用分数形式记祖冲之求得的“周率355、径率113”为355/113,并称之为“π的祖冲之分数值”,([10],页135—137)进而命名之为祖冲之率(以下简称祖率)([10],页50)。1917年,茅以升在《中国圆周率略史》中向国内介绍了三上义夫的发现[11]。中国数学史奠基人李俨、钱宝琮的著作中亦是以圆周率π解释刘祖关于周径率的成果[12][13]。由此,刘祖曾计算圆周率的近似值成为中外公认的事实。
根据以上所述,经明末清初西学东渐和近现代中外学人共同努力,刘徽算学中的圆和周径率最终分别被等同于欧氏几何学的Circle和π,从而将刘徽和祖冲之关于周径率的研究纳入世界数学发展之主流。但是,除了引证《墨经》关于圆的描述之外,对于上述等同性是否成立这一关键问题,尚未作深入探讨。对此作进一步研究,将导向对中国古代算学本土特性更为全面的理解。
1.2 中算史研究的本土化程序
正如后期维特根斯坦(Ludwig Wittgenstein)所述,词汇系统或语言在其使用过程中获取意义(5)见[14],维特根斯坦《哲学研究》中对语言游戏和词的含义的论述,如其第一部分编号1—31,37—43。。而语言使用是语境制约下的社会活动。语境主要包括如下要素:文化传统、基于文化传统的社会政治制度、处于文化传统和制度中的语言使用者的具体境况等。这些要素蕴含了文本形成和传播的动因、支撑文本的概念框架和预设,以及阐明文本中结论所依据的理由。正是在社会文化语境中,社会成员书写文本,进行交流和形成意义。因此,如果我们致力于把握文本的原意,那么只能依据文本在其中生成并获取意义社会文化语境,对文本进行解读和解释,将文本展现相应社会文化语境中自然生成的事物(6)文本研究人员所把握的文本原义,实际上是指:经过研究得到的关于原义的可靠假说。虽然,它不能等同于原义;但研究人员可以对它进行修改,使之与现有的古代文献和解读相一致;它与悖离原义的误解具有明显的区别。。这就是据中释中思想的合理性根源。
长久以来,在中国古代算学史研究中有一种方法论传统:尽量运用现代数学的概念与方法,从原始数学文献中发现数学事实,解释或证实所发现事实的数学意义及其正确性。其实质就是:采用主要源自西方的现代数学所具有的概念、原理和方法作为基本框架,分析、整理和解释中国古代文献;试图在中国传统算学发现相应于现代数学的成果。这就是中算史研究中所谓的“据西释中”方法。与之相对立的是“据中释中”:根据文献所处历史文化背景和中国古代已有的算学和其他领域的知识,拒绝利用中国古代文化中不曾具有的元素,对相应的古代数学文献进行解释(7)这一方法也可以扩展到其他传统文化研究领域,如佛教因明研究,见[15],页116—117。。
从语言人类学角度,不同的文化具有不同的语言,不同的语言各自具有划分世界和构建经验范畴的词汇系统。([16],页54—56)从中国古代社会文化语境及其从中产生的中国古代知识文本,与源于西方文化的语言及其学术思想大相径庭。从语用学的观点看,文本的意义既依赖于相应社会文化中业已形成的知识系统,又依赖于文本在其中出现的具体语境。因此,隶属于不同社会文化的文本的意义至多部分相同。如果用在西方或近现代文化中生成的知识和语言系统,去描述、解释和重构中国古代文本,那么这些被重构的文本将在西方或近现代文化中获取意义,而由此获取的意义是中国古代文本原先所不具有的。这就是我们据斥据西释中的原因。
在数学史研究方面,吴文俊分析了据西释中方法的一个典型案例——各家用添加平行线或代数方程方法对《海岛算经》诸题结论的证明,指出这类据西释中的方法易于引发的“错误”:“充其量只是用现代方法验证了刘徽的那些公式与定理都正确无误而已。这非特完全不足以反映当时的数学情况, 反而使古代辉煌的成就因之而淹没不彰。……这些错误方法已经泛滥于绝大多数流行的数学史著作之中,致使古代数学的真实情况不仅淹没不彰,而且面目全非,许多巴比伦神话、印度神话以及丢番图神话之所以产生,这是主要的原因之一。”([17],页128—129)简言之,这种方法导致了数学史研究中滥用现代数学概念与符号去接受古代数学成果的倾向[18]。
正因为如此,在“《海岛算经》古证探源”一文中,吴文俊提出古证复原三项原则。([19],页162)其核心是:要根据中国古代史实史料和当时当地算学实际发展水平,来描述当时当地的算学证明;不能套用现代的或其他地区的数学成果与方法,人为地构建预知的结果。因此,古证复原的先决条件是:按中算的本来面貌描述它的概念框架和研究方法。否则,中算包括古证的基本思想从一开始就被遮蔽了。这就是说:在研究中国古代算学史中的“证明”时,不能简单地“据西释中”。
为了克服上述方法论的局限,本文提出中算史本土化研究程序。其要点是:根据文献学的研究成果,选择合适文本;根据汉语言文字学,解读文本;运用历史学的方法,描述文本所在的社会文化语境;拒绝使用当时和当地不存在的理论框架和社会文化因素解读文本;仅将文本置于它所在的社会文化语境,根据当时语境解释文本,进而完成对文本的据中释中。
本文的目标是:根据中算史本土化研究程序,重新解读刘祖计算周径率概念及其计算方法,进而说明周径率异于圆周率;最后,在此基础上从古为今用的角度展望刘祖周径率研究的现代价值。
2 刘徽圆之概念及其起源
2.1 先秦学者的圆概念
在现代英文语境中,圆周率被定义为“the ratio of a circle’s circumference to its diameter”,记为π。在现代汉语中,它被译为:圆的周长与它的直径的比,同样也用希腊字母π标记。数学家已经证明π是无理数,而现代数学的工作之一就是计算它的近似值(8)近年来逐渐演变为对电子计算机的测试。。值得一提的是:数学史家一般认为,刘徽在《九章算术注》中计算了圆周率π的近似值(9)如文献[12],页20—22;[13],页65—68;[20],页249;[21],页225,234—243。。但是,如果刘徽眼中的“圆”及“周径率”的所指并非欧氏几何术语“圆”及“圆周率”的所指,而周径率和圆周率又具有不同的数学性质,那么我们就有理由怀疑这一看法的正确性。因此,要完成本文的目标,首先必须澄清刘徽的术语“圆”和“周径率”的含义。
根据刘徽所处时代已有的中国古代典籍记载,作为中国古代算学研究对象的圆,它是一类可感知、可想象的具体对象。首先,圆是用器具(圆)规制作而成:
《诗经·小雅·沔水》郑玄笺:“规者,正圆之器。”([22],页665)
《墨经·经上》:“圆,一中同长也。”([23],页311)
《墨经·经说上》:“圆,规写交也。”([23],页343)
《孟子·离娄上》:“不以规矩,不能成方圆。”([24],页475)
其中,“规写交也”描述一个经验可观察的作圆过程:一部具有两个距离固定之端点的器具,使其一端不动,移动另一端,保持“一中同长”即两端点距离不变,刻画一首尾相交的形状;从而具体说明了作圆器具和操作过程所具有的经验特征即“一中同长”,解释了《经》中相对应的条目。相比较而言,欧氏几何的圆是由定义给出的理想客体,用物理器具尺规作出的物理图形本身不是几何客体,而是一种象形文字,作为示意图展现几何客体的特性。
不仅如此,规和矩还是判定圆和方这类物体的方法:
《荀子·赋》(亦见《庄子》):“圆者中规,方者中矩。”([25],页474)
《周礼·考工记》:“规之以视其圆也,矩之以视其匡也。”(10)[22],页1077。矩原作“萭”,郑众云“书或作矩”。
其中,“视”表明:用规矩判方圆是一个经验直观的过程。而欧氏几何拒绝使用任何经验的方式来判定几何图形的性质。
最后,从方可做圆,破觚可为圆:
《周髀筭经》:“圆出于方,方出于矩。”“万物周事而圆方用焉,大匠造制而规矩设焉,或毁方而为圆,或毁圆而为方。”([26],页33,36)
《史记·酷吏列传》:“破觚而为圆。”([27],页3803)
这表明:有先秦时期学者认为,在日常生产实践中存在对方或觚进行加工的方法,其结果是可用规判定为圆的物体。
在这种观点之下,中算中的圆具有以下三大特征:
(1)用规矩可制作方圆,它们是可观察的具体物体;
(2)用规矩可判定方圆,判定的过程是日常的直观的;
(3)圆和方并非不相容,可从方做圆。
为了便于比较,用当下的术语说:规是物理器具,用它制作和判定的物体就是日常可触摸的物体。其次,作为器具制作而成的经验物体,圆的边缘不可能理想地光滑。因此,上述先秦文献中界定的圆从本性上不同于欧氏几何定义的作为理想物体的圆。
2.2 刘徽继承了先秦学者的圆概念
从刘徽《九章》注中“规”字的用法可以说明:他在注中所论及的圆具有上述三大特征,进而继承并沿用了先秦时期关于圆的这种界定(11)当然,无论先秦时期或刘徽,“圆”仍可用于指更广义的圆形,如“天圆地方”,“圆穹”等。不过本文考察的是作为古算计算对象的圆。。其中,符合上述特征1的情形有:
《九章筭术·少广章》:规之为圆囷,径二寸,高二寸(12)本文所引《九章》及其刘徽注,底本为[28]。并参考[29]之校勘,后文及注释亦简称“《汇校》本”。。
此处规作为动词使用,意谓用规制作圆形之体。
符合上述特征2的情形有:
《九章筭术·方田章》:弧体法当应规。
《九章筭术·方田章》:周三者,从其六觚之环耳。以推圆规多少之觉(较),乃弓之与弦也。
此处引文一表明:弧的形状应该与圆弧重合,其中规意指圆(13)参见[30]中66页注9。。引文二指出:若将周率三的六觚之环作为圆周,这个“圆周”与真正的圆周相比,就像弓和弦一样。显然,规在这一引文中用作判定圆的标准和规范。
进一步的证据是,在《九章》刘徽注中“规”共出现9次,其用法出处如下表:

表1 在《九章》刘徽注中“规”的用法出处
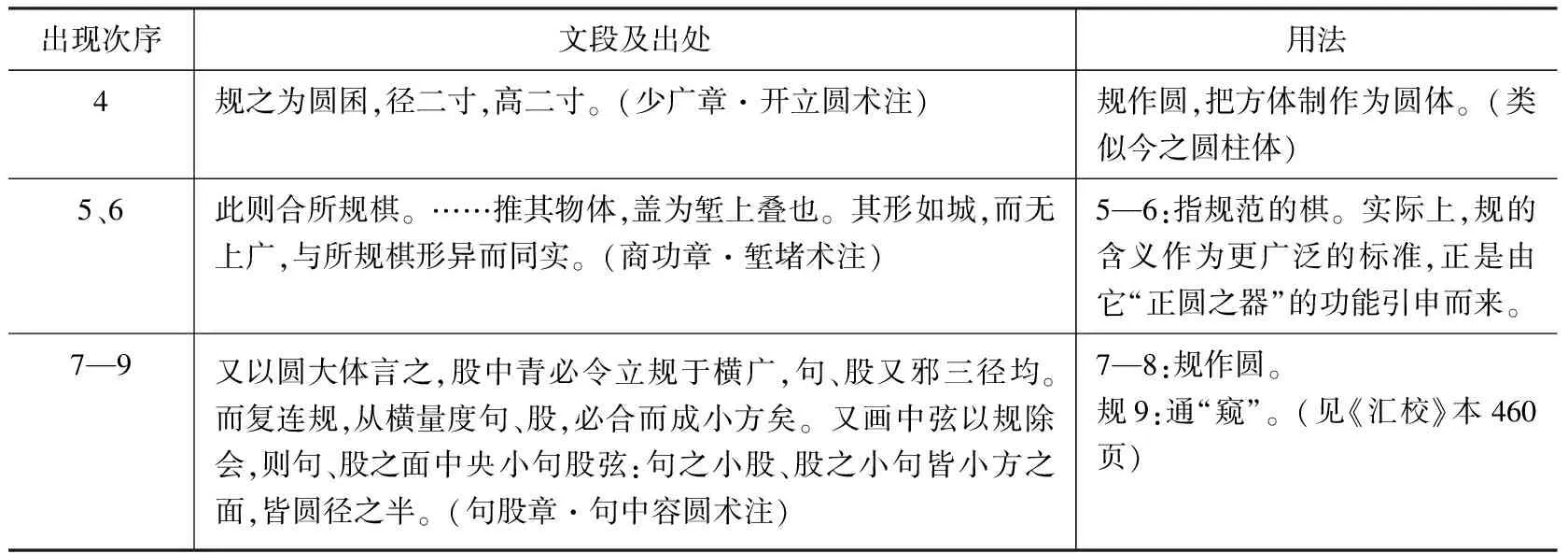
续表1
不难看出,除去堑堵术中,规意指“规范”和一处通假字;刘徽用“规”不出此三种含义:1.规作圆;2.规判圆/圆体;3.规就是指所作的圆/圆体(14)如同“范”以其作为铸造的标准器具一样,“规”在“规范”一词中很可能正是以“圆之标准”为义,才构成了其意为标准的“规范”语义。如果去掉现代汉语“规范”作为理解的中转,上表第5、6次“规”字可以理解为从“圆之标准”引申到“标准”。。
最后,刘徽在割圆术中割觚得圆,郭书春认为这源于汉代“破觚而为圆”的工艺(15)参见[31],页7。。这就是说,他所理解的圆可从方制作而得。值得一提的是:刘祖都曾用实物新莽嘉量的数据与自己的计算结果作比较,进一步验证所得结果。所有这一切表明:刘徽完全继承了上述先秦的圆概念,将圆看做一类日常可制作的物体。
2.3 刘徽圆之概念
更为重要的是,刘徽还进一步发展了先秦学者关于圆的思想;在其《九章筭术》圆田术注中系统地给出破觚为圆的方法;进而表明:圆不仅是一类日常物体,而且还可以被描述为一种特殊的多角形。他指出:
《九章筭术·圆田术注》:为图。以六觚之一面乘一弧半径,三之,得十二觚之幂。若又割之,次以十二觚之一面乘一弧之半径,六之,则得二十四觚之幂。割之弥细,所失弥少。割之又割,以至于不可割,则与圆周合体而无所失矣。
此处,割是指:从给定的某个圆内多角形(即觚形)出发,通过二分觚面(边)的方式,做出面数翻倍的圆内多角形的过程。在这一过程中,随多角形的面增加,面的长度变小。刘徽认为,割的过程将终止于其边不可再割的多角形,进而与圆周完全重合。由此,刘徽通过常识上可想象的加工过程,构造了一个其边不可再割的多角形,并将该物体视为可用于算学研究的对象。
刘徽对圆本性的看法根植于先秦学者关于物体有穷可分性的思想。如所周知,分割物体的过程是否有终点,这是先秦时期引人关注的论题之一:
《庄子·天下》引辩者论题:一尺之捶,日取其半,万世不竭。([32],页1099)
这就是所谓尺捶论题。其正题是:一尺长的物体可以无休止地二分;其反题是:二分过程在某一时刻终止于物体不可分的部分。墨子反对正题,支持反题:
《墨经·经下》:“非半弗斱,则不动,说在端。”([23],页326—327)
《墨经·经说下》:“非:斱半,进前取也。前,则中无为半,犹端也。前后取,则端中也。斱必半,毋与非半,不可斱也。”([23],页383—384)
《墨经·经上》:端,体之无厚而最前者也。([23],页312)
《庄子·养生主》:彼节者有间,而刀刃者无厚。以无厚入有间,……。([32],页125)
引文前两句表明:物体每次都截取其一半,当它不能被取半时,物体就是不可斫,而此不可分或取半的物体被称为端;端可以出现在物体的前部,也可以出现在它的中间。后三句表明: 端无厚无间,是物体极薄、不可分之部分。同时,根据上述对分物体的方式可知,被分物体有前部和后部,故有穷大小。因此,按照《墨经·经下》和《庄子·天下》对斱半和尺捶取半过程的描述,我们有:这类被分割的物体大小有穷;随着时间的展开逐次对它们进行分割;当物体分割至不可分的单元时,分割过程经有穷次运行后终止。
上述思想可表述成所谓的有穷可分命题:一个有穷物体经过有穷次分割,将终止于有穷大小的不可分割的部分。有穷可分思想恰是尺捶论题的反题,而与之相对立的正题就是物体无穷分解的观点。辩者的论题在同时代就遭到许多贬斥:《庄子·天下》中指出辩者“能胜人之口,不能服人之心”,([32],页1104)荀子斥为“治怪说,玩琦辞,甚察而不惠,辩而无用,多事而寡功,不可以为治纲纪”([25],页93—94)。汉代独尊儒术之后,辩者之说也随着名辩之学的衰落而乏人问津。
因而,刘徽“割至不可割”的论断正是上述有穷可分思想的体现[33]。在此思想的基础上,刘徽在九章圆田术注中对上述物体圆实施割觚,进而得出物体圆由不可割的觚面组成这一结论。值得一提的是:在注中,刘徽并没有实际完成割觚过程,上述圆概念是他在先秦有穷可分思想的基础上对日常实践中的割圆过程进行扩展的产物。我们称在上述割觚过程基础上形成的、其边不可割的多角形为“刘徽圆”。而刘徽所要计算的周径率正是刘徽圆的性质。
3 周径率误解
3.1 刘徽的率及其性质
本文所关心的是刘徽注中周径率的性质与计算。因此,必须先对率这一概念进行考察。对《九章筭术》及刘徽注中的率概念,郭书春和李继闵都曾进行过详尽的分析(16)参见[34]和[35]。亦参见林力娜法译本《九章筭术》术语表中的“率”字条([36],页956—958)。。刘徽是首位对率做出清晰界定的中算家(参见[35],页25)。他在《九章·经分术注》指出:
凡数相与者谓之率。率者,自相与通。有分则可散,分重叠则约也;等除法实,相与率也。(17)依《汇校》本34页校勘记校改。
郭书春([35],页25)指出,这里数相当于今天数学中的量,相与则是相关性。换言之,相关事物的量构成了率,以周径之长具有的关系为例,《九章》所用率为“周三径一”。为了行文方便,我们将这一表达相与关系的率称为率关系;将相与关系中的某个事物或某个项的具体数量,称为(某个物的)率,在上例中即为:周率三,径率一。
上述引文中“有分则可散,分重叠则约也”一句指出:对各率中包含(筹筭)分数的情形可以运用《九章》中的分数计算方法进行通分和约分。然后刘徽提出了“等除法实”,即各率同时除以“等数”(见约分术),由此可得到“相与率”。更具体地说,“率者,自相与通”和《九章·衰分章注》:“凡所得率者,细则俱细,粗则俱粗,两数相抱而已。”(18)依《汇校》本121页,125页校勘记校改。这两句表述了率关系的一个性质:各率乘或除同一个数,仍然描述原来的率关系(19)郭书春([35],页35)和李继闵([34],页233)都用比例关系和线性关系来解释率关系。换言之,一个率关系可以用多组率来描述,而将其中的一组率乘以不同的数就得到其他组率。最后,根据“等除法实”,刘徽界定相与率:相与率是同一率关系中这样一组率,由这一率关系中的其他率关系对等数进行等除得到。刘徽所求“周径相与之率”中“相与率”概念亦如此意(20)郭书春([35],页27)指出,这相当于互素概念。李继闵也有同样结论([34],页232),并指出刘徽实际行文中并不严格区分“率”和“相与率”。。
刘徽不仅界定了相与率,还给出了相应的理论依据。他在今有术注中指出:
少者多之始,一者数之母,故为率者必等之于一。据粟率五、粝率三,是粟五而为一,粝米三而为一也。欲化粟为米者,粟当先本是一。一者,谓以五约之,令五而为一也。讫,乃以三乘之,令一而为三。如是,则率至于一,以五为三矣。
这一段引文给出了确定率关系的原则:“为率者必等之于一”(21)郭书春([35],页26)认为这也是确定率的方法。。同时,运用率关系“粟五粝三”的案例,对这一原则及其运用进行说明。
在率关系中,某物的率是一个数量;该数量(单位随物而定)的某物能看作为“一”。此处的“一”是物品互换中的“一份”([35],页26;[34],页229)。例如:“粟五为一”和“粝三为一”分别是说:五个单位的粟可看作一(份),三个单位的粝可看作一(份)。根据“为率者必等之于一”的原则,若粟与粝之间有率关系,那么一份粟对等于一份的粝;而两者间的率关系就是:“粟率五、粝率三”。若化粟为粝,先要看已有的粟中包含多少份粟。这就是将粟的数量除以粟率5;再将粟的份数乘以粝的率3,得到份数相同的粝的数量。由此,根据粟与粝之间的率关系,一定数量的粟对等于份数相同但数量不同的粝。
不仅如此,上述引文还指出:“少者多之始,一者数之母”。刻画了数量的基本性质。首先,它以对仗的形式表明:事物的量与率之间有对应关系。其次,基于这一关系,前一句为后一句提供理由,说明数量由一而生。换言之,刘徽的率理论用两种方式刻画事物的数量关系。一方面,用度量单位描述事物数量的大小(以单位记),这是具体的情形;另一方面,从率的角度,对关联的事物用单位“一”描述——它们具有同样多的“一”。例如:在粟粝交换关系中,粟10斗和粝6斗对等,而以率粟5粝3论,此实例中粟粝皆是二份“一”。
郭书春([35],页26)对刘徽上述思想的方法论特征进行了总结:“衡量一组物中诸物的率,要有一个公度,这个公度就是单位度量,亦即一,刘徽称之为‘数之母’。”李国伟进而指出:一者数之母的思想实质上体现的中国古代数学的朴素信念,即几何物件都能用适当选择的单位度量出一个数值来[37]。因此,在刘徽看来,任何一个“数”都是由一生成,周径率的精确值也是如此。用现在的话说:周径率是一组整数。
3.2 周径率及其近似值
在刘徽之前,人们就认识到了圆的周与径之间具有相关性。《九章筭术》取周径率为周三径一。在《九章筭术·圆田术注》中,刘徽继承并发展了这一观点:
此以周径,谓至然之数,非周三径一之率也。……方圆之率,诚著于近,则虽远可知也。
根据引文的前一句话,刘徽认为:周三径一中的“周三”不是周率的准确值,故不能用来准确地表达周和径之间的率关系;而准确的周径率,即至然之数,是周率与径率的准确值之间的关系。由此,如同《九章筭术》作者,刘徽肯定周径之间存在率关系。另一方面,根据刘徽的率理论,周径率作为一个率关系的特例,它由一对相互之间没有等数的数组成,它们分别对应于周率和径率的准确值。
进一步的问题是如何求得周径率。刘徽通过割圆过程构造刘徽圆,论证了圆田术的正确,为计算周径率的方法奠定了基础。根据这一方法,当圆内割觚割至不可割时,得到的觚就是刘徽圆;所谓周径率就是刘徽圆的周与径之间的相与之率。不过,刘徽并未将圆“割至不可割”,只是从理论上对之进行分析。所以在实际计算中,刘徽使用的是一种近似计算方法:先给定圆的径,从径二尺的圆开始割觚,逐次求各觚的面,亦即得到觚周,再通过圆田术求觚幂。由于实际上没有将觚割至不可割,他先计算实际所得觚的幂;根据这一觚幂,对圆幂做出估计,再用圆田术“半周半径相乘为圆幂”逆求圆周。事实上,刘徽对192觚实施上述方法,得到他的第一组周径率【周157,径50】。另一方面,求觚面过程中要用到开方术,从而多半要遇到开方不尽的问题。在实际计算中,刘徽的处理方法是:把开方的结果截止在某个长度单位上(一般是忽位),以满足实际计算需求和可行性。
刘徽深知其计算结果只是周径率的近似值。对于上述结果,他指出:“周率犹为微少。”其后,刘徽又总结道,“新术径率犹当微少。则据周以求径,则失之长;据径以求周,则失之短……”不仅如此,刘徽还给出由逐次获取的觚幂构成的序列,认为序列各项之间的差值构成率关系;从而“以率消息”,以此估算192觚幂与圆幂差值,求得近似圆幂;再割觚到3072觚幂来验算,最终求得另一组率【周3927,径1250】(22)具体讨论,可参考[38],其中,朱一文认为刘徽估算的是192觚幂与3072觚幂差值,再以后者来定圆幂。本文暂不分析刘徽的“以率消息”的具体细节。另,对这个率的相关记载,也有说法认为是祖冲之注(如李俨),本文采纳钱宝琮的意见[39],认为是刘徽创作。。在实际应用中,刘徽推荐使用第一组率,对此组结果的评价则是“盖尽其纤微矣”。所有这一切表明:刘徽本人清楚地认识的到:他给出的均只是周径率的近似值,而不是“至然之数”(23)目前来看,刘徽的方法从本质上也只能给出近似值。不过,刘徽心目中理想的周径率也是“至然之数”组成的率,因而这个理想的周径率也必须满足前述所总结的率的重要性质:以一组率数组成的数量关系,且“等之于一”。。
对于周径率计算,中国古代数学家中祖冲之的成果最为显赫。据《隋书》载:“宋末南徐州从事史祖冲之更开密法。以圆径一亿为一丈,圆周盈数三丈一尺四寸一分五厘九毫二秒七忽,朒数三丈一尺四寸一分五厘九毫二秒六忽,正数在盈朒二限之间。密率圆径一百一十三,圆周三百五十五。约率圆径七,周二十二”([40],页388)。此处的关键是:祖冲之明确提出有圆周“正数”存在,即存在圆周准确值,而上述密、约两率是周径率的近似值而非精确值。
可惜的是,记载祖冲之如何计算周径率的著作今已不存。对于祖冲之如何求“圆周正数”,李俨([12],页28)认为“或因刘徽割圆术方法继续推算”,钱宝琮([13],页95)假定“他采用和刘徽割圆术相仿的方法”,《九章》李淳风注云:“徽虽出斯二法,终不能究其纤毫也。冲之以其不精,就中更推其数”。清《畴人传》:“徽创以六觚之面割之……厥后祖冲之更开密法,仍是割之又割耳,未能于徽注之外,别立新术也。”《中国数学史大系》中,何文炯([41],页121—122)据此二文献记载,认为祖冲之“可能延续刘徽的工作”。最后,《中国科学技术史·数学卷》([3],页270)指出:“一般认为,他(指祖冲之)是利用刘徽的计算圆周率的程序求得π的8位有效数字的。”因而,在没有发现新的文献材料之前,本文亦沿用上述结论(24)对于祖冲之究竟如何求出约率(355,113)和密率(22,7),学界尚未有定论。本文所关注亦非讨论祖冲之如何从“正数”范围求得上述两个近似的率关系的具体方法。。
综上所述,刘徽采用基于日常实践的有穷方法研究和阐明了周径相与之率的基本性质。该方法的要点是:圆是日常实践活动中可触摸的物体,而物体有穷可分性,即通过有穷次切割可将有穷物体分割成有穷个不可再分割的部分;数量的一可公度性,即在恰当的单位下有穷事物的量总可用某一单位来度量或整数表达([21],页146)。在这一方法的基础上,刘徽构造刘徽圆,明确相与率概念,将周径长度之间恒定的共变关系表达为周径相与之率,即一组相互关联的没有等数的整数,最后计算周径相与之率的近似值。而后,根据我国学者的考证与分析,正是沿用了这一理论途径,祖冲之得到了他的周径率。
3.3 周径率与π的比较
在欧氏几何中,圆周(circle,或欧氏圆)被定义为:距平面上一定点之距离为定长的点的轨迹,而定点称为圆心;连结圆周上两点并过圆心的线段为直径([42],页4—5)。而线是无穷多点的轨迹,线只有长度,但没有宽度;平面只有宽度和长度,但没有厚度;图形是点线面体的任意集合([42],页1)。因此,欧氏圆、圆周和直径作为平面几何图形,圆周与直径之比(ratio)的圆周率只是这些几何图形之间的关系。欧氏几何学用公理化的方法描述这些几何对象及其关系的性质。基于上述定义和公理给定的基本概念,圆的相关性质就可以被演绎地推导出来,如圆周曲线的连续性,圆周率π具有无理性和超越性等;而欧氏几何学家给出的是π的近似值。
相应地,中国算学家刘徽继承和发展先秦学者关于方圆是可触摸物体的观点和物体有穷可分思想;认为圆是其边不可再割的多角形物体;周径率则是能够从可触摸物体加工而成的物体的数量关系。同时,根据刘徽所阐发的数一可共度和相与之率的思想,周径率的精确值是一组整数。最后,刘祖在日常实践活动有穷方法的基础上设计算法,通过计算给出一组周径率的近似值。
两相比较,不难得出如下结论:从研究对象看,刘徽圆不同于欧氏几何圆,刘祖所计算的周径率不是圆周率;从数学性质看,能构成周径率的周径之量须“等之于一”,其精确值是一组整数,圆周率的精确值是无理数π;从计算结果看,刘祖计算的是周径率而不是π的近似值。值得一提的是:周率和径率之比值这一类概念未于刘祖二人所遗留的文字。李继闵早就指出,古今“率”含义不同,古率并非比例值。([34],页241—242)实际上,“率”字用来指比值是始于近代的用法。如果我们回到现代数学的语境,用今天之比值来描述古算周径率的话,那么也可以说:中国古代的圆周和直径之比值是一个有理数。
虽然,在研究对象、方法和结论等方面,上述源于两种不同传统的理论大相径庭。然而,这绝不意味着两者之间不具可比性。从应用的角度看,它们是用不同的方法处理相同的日常可触摸物体。当欧氏传统学者面临一个经验的具体的圆形物体的计算问题时,他首先将该经验性圆形物投射为欧氏圆,或用后者描述前者;然后采用欧氏几何处理相应的计算问题,得到相应的结论;最后对该结论做经验解释,使得解释后的结论成为原圆形物计算问题的解。相较之下,当中算传统的学者面临同样的计算问题时,他会将该圆形物视为刘徽圆,采用中算的方法处理相应的计算问题,并将计算结果视为原圆形物计算问题的解。根据历史数据,在涉及圆形物的周长和直径关系的应用领域,刘徽的方法在较长的历史时期内都能取得比欧氏几何更为精确的计算结果。这种可比性或许也是将周径率误认为圆周率的原因之一。
4 总结与展望
本文按照中算史本土化研究程序,采用据中释中的方法研究刘徽《九章筭术注》中的周径率理论,主要结论可概括如下:在先秦文化的背景下,刘徽采用有穷主义方法构建刘徽圆;在“等之于一”的率概念基础上,提出不同于当今平面几何中圆周率概念的周径率概念,并计算了周径率的近似值。由此展现了中算的特点。
反观当今科技,对于计算机和人脑信息处理过程而言,信息被有穷编码、有穷输入、有穷步加工、有穷输出信息,故整个过程是有穷的。同时,目前的科学认识支持如下观点:我们人类认知系统是有穷的和离散的。因此,如何采用有穷方法处理经验对象?这是一个值得关注的问题。
本文的研究表明:由刘徽发展起来的基于经验的有穷方法,能直接用于解决一些涉及经验对象计算问题,在历史上曾具有较强的解决问题能力。我国科技发展的经验表明:借鉴本土历史文化资源,能够为解决当代问题提供有价值的启发。因此,我们将进一步采用据中释中的方法,探讨刘徽处理经验图形的有穷方法,在当代科学的背景下古为今用,探索更有效的信息和数据处理方法,为解决上述问题作出努力。
致 谢感谢朱一文副教授,他在本文写作过程中提供了许多帮助和有益的意见;感谢韩琦教授,他对本文提供了文献和史料上的帮助和宝贵的修改意见。本文的不足与舛误,责任由作者承担。
