一种近景大斜角的限界检测相机标定方法
2019-04-16陈猛何越磊龚佩毅李再帏路宏遥
陈猛,何越磊,龚佩毅,李再帏,路宏遥
一种近景大斜角的限界检测相机标定方法
陈猛1,何越磊1,龚佩毅2,李再帏1,路宏遥1
(1. 上海工程技术大学 城市轨道交通学院,上海 201620; 2. 上海欣铁机电科技有限公司,上海 201100)
研究一种基于单目视觉的非接触式站台限界检测系统,并针对近景大范围下相机标定的问题,提出一种基于大型点阵标定板的新的综合标定方法。提取有效标定区域进行预处理,并提出一种局部阈值迭代分割的方法分割出基准圆,然后提取圆心坐标并编码,最后利用透视变换求出最优变换矩阵进行图像矫正还原,像素标定误差可达到2以内。经在上海地铁的现场测试验证,本文方法标定后的检测系统可准确获取站台断面轮廓几何尺寸,多次反复测量后轨距精度在±1 mm以内,站台高度和站台距离精度可达到±5 mm以内。
站台限界;近景大斜角;局部阈值迭代分割;最优变换矩阵
地铁站台限界是为确保安全行车,列车与沿线建筑物、设备之间的相互空间关系[1],因此,站台限界检测是在地铁车辆运营期日常检测的一个重要工作。近几年,在地铁限界检测领域,除了采用传统的接触式测量方法外,非接触式机器视觉测量的方法也逐步被应用。在高精度的视觉测量中,系统标定是影响系统精度的一个关键环节[2]。目前,常用的平面标定板为棋盘格式[3]和圆点阵列式[4]。其中,针对棋盘格的有张正友标定法[5],利用Harrris角点检测寻找世界坐标与图像坐标之间的关系,降低了算法的复杂度。然而,在棋盘格图像中,由于图像角点处的模糊现象使得实际角点附近的一个或者多个点的Harris响应值较高,角点位置的确定通常会出现偏差。卜鹏辉等[6−7]分别对张正友标定法进行改进,实现了立体视觉的全自动化和大视场标定,但其均是基于多目视觉和多幅棋盘格图像进行标定,操作起来复杂繁琐,工作量大。圆形标志点由于其识别方便且定位精度高的优点,在立体视觉领域得到广泛应用。梁力等[8−10]在圆形标志点提取的算法方面进行了大量研究,使用渐变圆形或者大、小相间实心圆作为靶点进行标定,使用的靶标为圆形渐变模板[8]、渐变标定板[9−10],徐佳磊等[11]指出,在地铁运行安全检测中对站台几何关系的测量,往往需要近景大范围摄影测量,所采集到的图像产生畸变较大,特征提取困难,而上述标定算法中,相机与靶标夹角较小,采集的靶标图像往往畸变不大,特征点提取方便,不适应于本系统标定要求。本文提出一种近景大斜角的站台限界检测系统相机标定方法,基于大型点阵标定板,利用提出的局部阈值迭代分割和质心算法识别定位标定板中的基准圆并提取圆心坐标,依据圆心特征点进行图像矫正还原,完成相机标定工作。
1 标定模型建立
1.1 摄像机标定模型建立
根据测量原理,建立的近景大斜角的相机标定模型如图1所示。在相机标定时,系统激光发生器所发出的结构光光带与标定板处于同一切面,而系统工装的设计、仪器的操作和相机参数的设置,确保了相机的与标定板的夹角、采集图像的画幅在采集过程的不变性,即保证多次采集到的标定板图像的一致。
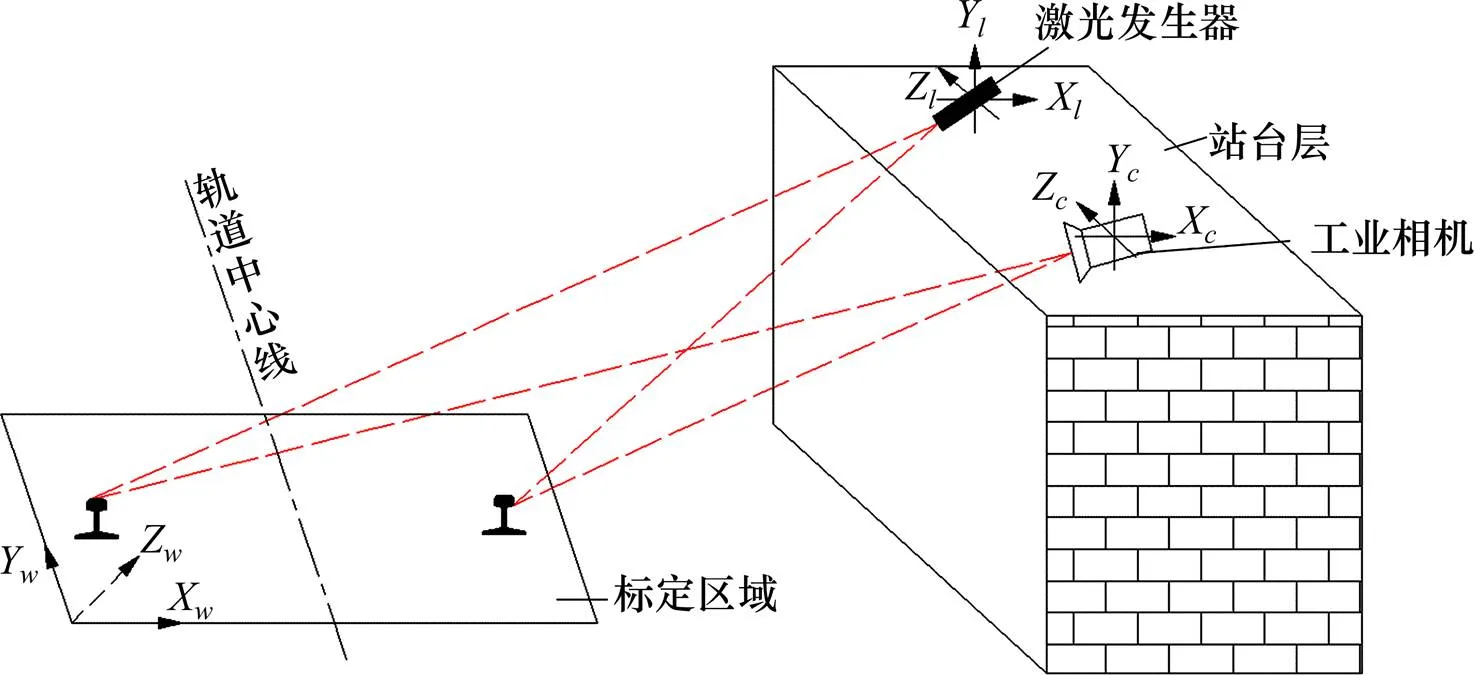
图1 相机标定模型
1.2 标定区域选择
采用圆心间距为40 mm,半径为20 mm,加工误差为±0.02 mm的大型点阵标定板,在图1所示的相机标定模型下,实际拍摄的标定板图像如图2所示,拍摄的钢轨图像如图3所示。
由于相机在同一拍摄模型下分别拍摄标定板和钢轨轮廓,2幅图具有相同的尺寸大小,将2幅图按不同的透视度比例融合在一起,查看钢轨廓形在标定板中的位置,并选定标定区域,如图4(a)中框线所示。为了提高测量标定精度,综合考虑相机的视场、分辨率和钢轨廓形,选取的标定区域为21行56列基准点圆范围。该区域的选择避免了在进行基准圆的圆心距标定时,边缘位置的变化对标定的像素精度的影响。
实际上,站台限界的现场测量受灯光影响较大,比如站台侧面广告灯光、站台层天花板的灯光,在选定的标定板区域用白色胶带布上一些干扰条件,增加特征基准圆分割难度,如图4(b),然后再进行图像处理,这样会使本站台限界系统在实际应用中适应性更强。

图2 标定板

图3 钢轨轮廓

(a) 标定区域选定;(b) 提取的标定区域
2 基准圆圆心提取及图像变换
世界坐标系中,标定板上基准圆变换后在图像中显示为椭圆,此外,如图6,左下角的标定板畸变更大,矫正困难。因此,对标定区域的图像处理结果的好坏将直接影响基准圆的提取和圆心的定位。本文先采用高斯模糊算法[12]对图像进行降噪,其次基于阈值分割法[13]并结合灰度直方图提出局部阈值迭代法分割出基准圆,然后采用连通域的原理[14]和求取图像质心的方法对二值化后的椭圆图像进行圆心坐标提取,最后根据不同大小的四边形角点圆心点坐标作为特征点求取变换矩阵,并结合误差分析得出最优变换矩阵作为图像的全局变换系数进行图像变换矫正。
2.1 基准圆的识别定位
阈值分割法主要分为全局阈值分割法和局部阈值分割法,全局阈值分割法代表的有大津阈值法,简称Otsu。它是按图像的灰度特性,将图像分成背景和目标2部分。背景和目标之间的类间方差越大,说明构成图像的2部分的差别越大,当部分目标错分为背景或部分背景错分为目标都会导致2部分差别变小。因此,使类间方差最大的分割意味着错分概率最小。然而对于本文中标定图像,由于设置干扰点以及近景大斜角拍摄标定板,噪声干扰大、光照不均匀、图像畸变较大的特点,使用Otsu算法获得的全局单一阈值往往不能兼顾图像各个区域的实际情况,难以进行有效的图像分割。
结合大津阈值法和图像标定区域中各子区域灰度值的变化,提出一种自适应性较强的局部阈值迭代分割法,实现流程如图5所示。
通过多次试验,图像子区域的最佳阈值分割范围为30~50。
图6给出了全局阈值分割法和本文所提的阈值分割法的二值化图像。
2.2 圆心提取
连通区域(Connected Component)一般是指图像中具有相同像素值且位置相邻的前景像素点组成的图像区域。
常用的邻接关系包含2种:4邻域和8邻域。4邻域一共4个点,若存在像素点,则四邻域为该点的上、下、左、右相邻点,8邻域除了包含4邻域中的点外,还包括4个对角点。本文基于8邻域标记算法和质心定位算法,并结合所采用的大型点阵标定板,实现基准圆圆心坐标的提取并进行编码,如图7。
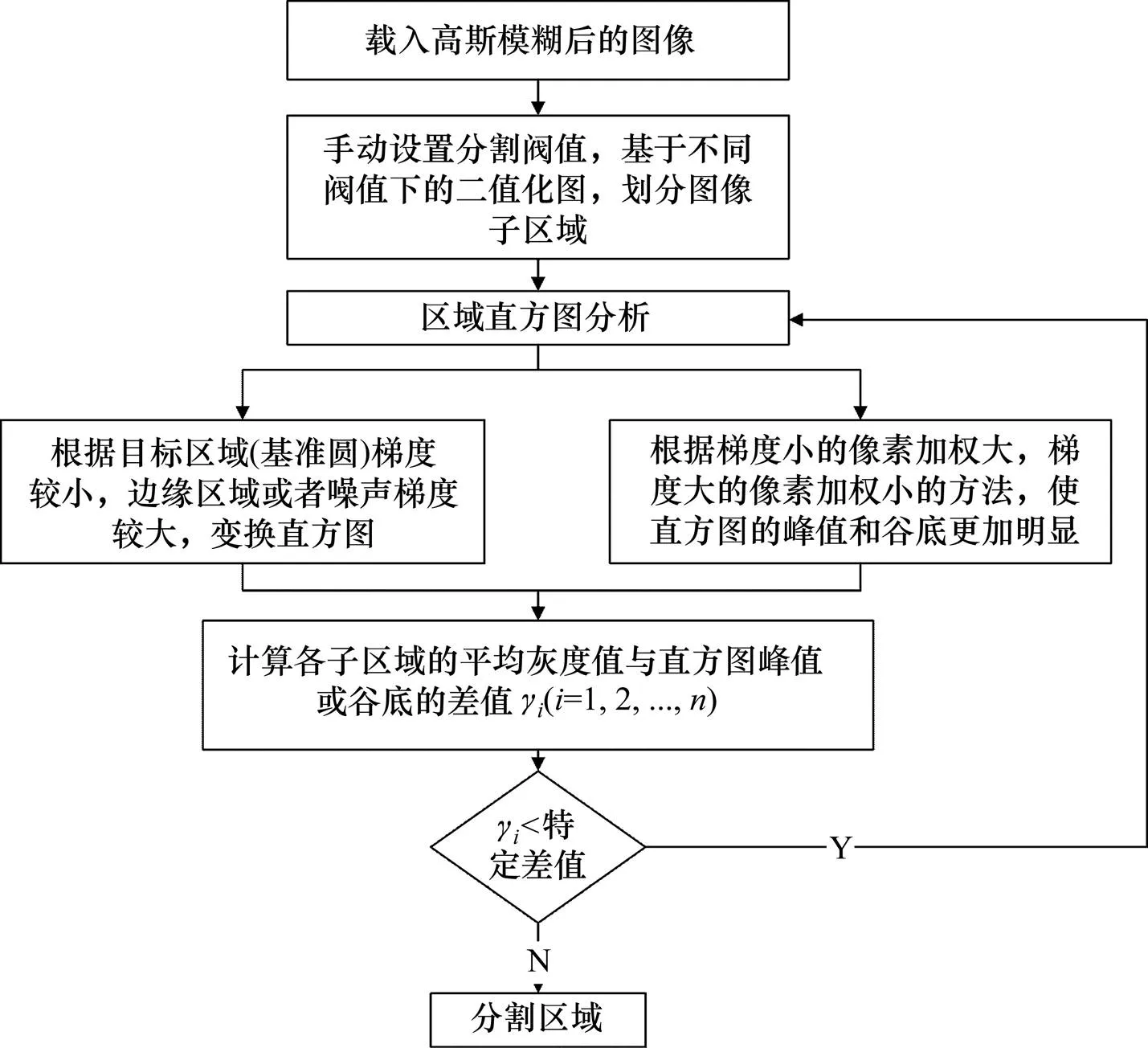
图5 局部自适应迭代分割

(a) 全局阈值分割;(b) 传统局部阈值;(c) 本文方法
2.3 图像变换


(a) 圆心标记;(b) 圆心编码

图8 物点、像点的坐标关系
透视变换[15]本质是将图像投影到一个新的视平面,通用的公式为:




由式(2)~(3)可推导得到:






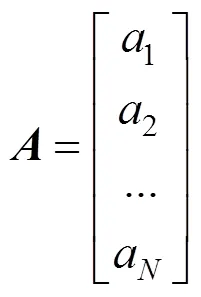
同样的对应可得到矩阵:
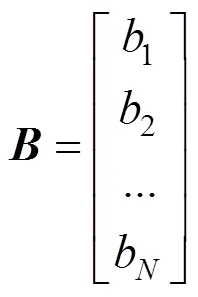
求解矩阵:
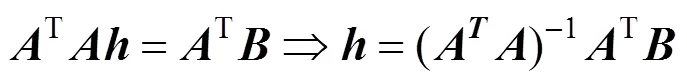
得出的即为所求的透视变换矩阵。显然,矩阵中存在8个未知量,需要提供至少4个点对进行求解,依次选取原图像中不同大小四边形4个角点基准圆圆心坐标,构建8个方程并求解。
结合本文采用的标定板,利用matlab软件实现图像变换,具体操作步骤如下。
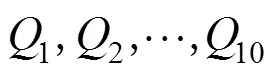

Step 3:构建矩阵和,并根据式(11)求解透视变换矩阵1;
Step 4:根据变换矩阵1,求取图像变换后的4个顶点11,12,13和14的坐标值;
Step 5:从变换后的图像中逆向寻找原图像中像素值,对于原图像变换到新图像中消失的像素点值,采用双线性插值的方法填补;
Step 6:按本文所述的圆心提取方法提取变换后基准圆圆心坐标并输出坐标文件1;
Step 7:依次选取四边形2,…,104个角点基准圆的圆心作为变换的特征点,重复Step 2~Step 6的步骤,依次计算出变换矩阵2,…,10和坐标文件2,…,10;
Step 8:通过3.1的方法分析图像变换后基准圆圆心间距的理论与实际差值,选取差值最小的一组变换矩阵作最优解。
根据上述的操作步骤,得到图像透视变换的最优化矩阵为:

变换后的标定板图像及圆心提取如图9所示。
(a) 变换后的标定板图像;(b) 圆心编码
图9 变换后的图像结果
Fig. 9 Transformed image results
3 实验验证
为了分析本文的标定算法的准确性和系统精度,从2个方面对标定的精度进行验证,一方面从每个相邻基准圆圆心间的像素长度实际值与理论值进行误差分析,另外一方面利用本系统在地铁现场实测的站台限界的几何轮廓值与目前地铁上常用的检测手段检测出的轮廓值进行对比,分析误差。
3.1 标定精度的鲁棒性
根据标定板基准点圆在透视变换后圆心坐标,计算变换后所有相邻基准圆圆心距1,2,…,2275,已知变换后的基准圆圆心距,计算圆心距绝对误差值Δ:

根据式(13)计算的结果可得到圆心距绝对误差值分布如图10所示。
(a) 竖向圆心距绝对差值(20*56);(b) 横向圆心距绝对差值(21*55)
图10 圆心距绝对值误差分布
Fig. 10 Absolute error distribution of the center-to-center distance
3.2 现场实测的数据对比
为了进一步验证本文标定方法的鲁棒性和系统精度,在上海某地铁站进行现场测试,图11为现场测试的图像。
对轨距、站台高度(钢轨顶面至站台层距离)和站台距离(轨道中心线至橡胶条边缘的距离)3个几何尺寸进行检测,随机抽选地铁上行线或者下行线中5个站台断面,并通过地铁站台检测常用的检测工具轨距尺(精度±0.5 mm)、站台尺(精度±1 mm)和本系统对每个断面分别连续采集5次,并对5次的采集数据平均值进行误差分析,验证本系统数据检测的有效性和稳定性。

(a) 仪器采集轮廓;(b) 相机滤光后的断面图

表1 轨距数据分析

表2 站台高度数据分析

表3 站台距离数据分析
由表1~3可知,2种检测方式采集的轨距平均值最大绝对误差为0.2 mm,最大绝对标准差差值0.099 5 mm,最大检测误差为0.6 mm,满足《城市轨道交通工程测量规范》(GB50308—2008)的要求。站台高度平均值最大绝对误差为0.6 mm,最大绝对标准差差值0.387 3 mm;站台距离平均值最大绝对误差为0.4 mm,最大绝对标准差差值0.295 4 mm。说明2种检测方式的测量数据基本吻合,且最大检测误差均满足《地铁限界标准》(CJJ 96—2003)的要求。以上检测结果的数据分析验证了本文所述标定方法的标定精度的可靠性。
4 结论
1) 在近景大范围视角下,系统相机采集的靶标图像畸变较大,基于大型点阵标定板的综合标定方法,选择出关键的标定区域,并采用高斯模糊进行图像预处理,提出局部阈值迭代分割法有效地分割出基准圆并提取圆心,根据圆心找出特征值并求出最优透视变换矩阵进行图像变换。
2) 经验证,本文的标定方法具有较高的鲁棒性,像素误差在2以内且在现场测试中,轨距检测精度能达到±1 mm以内,站台距离和站台高度在±5 mm以内,满足规范测量要求。
3) 与传统的检测工具不同,本检测仪器便携、可拆卸,同时,操作人员无须进入站台轨行区作业,测量速度快,系统带有水平调节可保证测量基准的唯一性,测量精度高,能够满足地铁停运作业的时间和精度要求。
[1] 李甍, 于龙, 张冬凯. 地铁设备限界随机因素分析[J].铁道科学与工程学报, 2015, 12(3): 657−662. LI Wei, YU Long, ZHANG Dongkai. Analysis on random factors of subway equipment boundary[J]. Journal of Railway Science and Engineering, 2015, 12(3): 657−662.
[2] 史红梅, 吴攀, 余祖俊, 等. 基于点集配准的非接触式地铁限界检测系统标定方法研究[J]. 铁道学报, 2014, 36(11): 16−22. SHI Hongmei, WU Pan, YU Zujun, et al. Study on calibration method of contactless metro boundary detection system based on point set registration[J]. Journal of the China Railway Society, 2014, 36(11): 16−22.
[3] 钱丽丹, 杨军伟. 基于精密运动的激光平面标定方法[J]. 计算机工程, 2013, 39(4): 318−321. QIAN Lidan, YANG Junwei. Laser plane calibration method based on precise motion[J]. Computer Engineering, 2013, 39(4): 318−321.
[4] 吴凡路, 刘建军, 任鑫, 等. 基于圆形标志点的深空探测全景相机标定方法[J]. 光学学报, 2013, 33(11): 147−153. WU Fanlu, LIU Jianjun, REN Xin, et al. Calibration method of deep space exploration panoramic camera based on circular landmarks[J]. Journal of Optics, 2013, 33(11): 147−153.
[5] ZHANG Z Y. A flexible new technique for camera calibration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2000, 22(11): 1330−1334.
[6] 卜鹏辉, 赵宏, 谷飞飞, 等. 一种基于平面靶标的全自动标定方法[J]. 光学学报, 2014, 34(10): 200−204. BU Penghui, ZHAO Hong, GU Feifei, et al. A fully automatic calibration method based on planar targets[J]. Acta Optica Sinica, 2014, 34(10): 200−204.
[7] 刘震, 尚砚娜. 立体视觉传感器的一种灵活靶标新标定方法[J]. 光学学报, 2013, 33(3): 205−211. LIU Zhen, SHANG Yanna. A new calibration method for flexible targets of stereo vision sensors[J]. Acta Optica Sinica, 2013, 33(3): 205−211.
[8] 梁力, 尹东斐, 王川. 高精度摄像机标定模板的设计及识别算法[J]. 西安交通大学学报, 2011, 45(4): 82−85. LIANG Li, YIN Dongfei, WANG Chuan. Design and recognition algorithm of high-precision camera calibration template[J]. Journal of Xi’an Jiaotong University, 2011, 45(4): 82−85.
[9] 夏仁波, 刘伟军, 赵吉宾, 等. 基于圆形标志点的全自动相机标定方法[J]. 仪器仪表学报, 2009, 30(2): 368−373. XIA Renbo, LIU Weijun, ZHAO Jibin, et al. Automatic camera calibration method based on circular marker[J]. Chinese Journal of Scientific Instrument, 2009, 30(2): 368−373.
[10] 胡浩, 梁晋, 唐正宗, 等. 大视场多像机视频测量系统的全局标定[J]. 光学精密工程, 2012, 20(2): 369−378. HU Hao, LIANG Jin, TANG Zhengzong, et al. Global calibration of video camera measurement system for large field of view[J]. Optics and Precision Engineering, 2012, 20(2): 369−378.
[11] 余佳磊, 何越磊, 龚佩毅, 等. 基于区域生长重心的大型多阵列圆标定板基准点的提取技术[J]. 计算机测量与控制, 2017, 25(11): 146−149. YU Jialei, HE Yuelei, GONG Peiyi, et al. Extraction techniques of large-scale multi-array fixed plate reference points based on regional growing gravity[J]. Computer Measurement & Control, 2017, 25(11): 146−149.
[12] Flusser J, Farokhi S, Hoschl C, et al. Recognition of images degraded by Gaussian blur[J]. IEEE transactions on image processing: a publication of the IEEE Signal Processing Society, 2016, 25(2): 88−99.
[13] Sezgin M, Sankur B. Survey over image thresholding techniques and quantitative performance evaluation[J]. Journal of Electronic Imaging, 2004, 13(1): 146−168.
[14] 闫建平, 梁强, 李尊芝, 等. 连通域标识法在FMI图像溶洞信息定量拾取中的应用[J]. 地球物理学报, 2016, 59(12): 4759−4770. YAN Jianping, LIANG Qiang, LI Zunzhi, et al. Application of connected domain identification method in quantitative pickup of karst information in fmi images[J]. Chinese Journal of Geophysics, 2016, 59(12): 4759− 4770.
[15] 蔡国榕, 李绍滋, 吴云东, 等. 一种透视不变的图像匹配算法[J]. 自动化学报, 2013, 39(7): 1053−1061. CAI Guorong, LI Shaozi, WU Yundong, et al. A perspective-invariant image matching algorithm[J]. Acta Automatica Sinica, 2013, 39(7): 1053−1061.
A close-range detector camera calibration method with high close angle
CHEN Meng1, HE Yuelei1, GONG Peiyi2, LI Zaiwei1, LU Hongyao1
(1. School of Urban Transportation, Shanghai University of Engineering Science, Shanghai 201620, China; 2.Shanghai Xintie Mechanical & Electrical Technology Co., Ltd, Shanghai 201100, China)
In this paper, a non-contact platform limit detection system based on monocular vision was studied, and a new comprehensive calibration method based on large-scale lattice calibration plate was proposed for the problem of camera calibration under a wide range of close-range vision. The effective calibration region was extracted for preprocessing. And this paper propose a local threshold iterative segmentation method to segment the reference circle, then extracts the center coordinates and encode, and finally uses the perspective transformation to find the optimal transformation matrix for image correction and reduction, pixel calibration error can be Within 2. After field tests in the Shanghai subway, the detection system after calibration of this method can accurately obtain the geometrical dimensions of the platform section profile. After repeated measurements, the gauge accuracy is within ± 1mm, and the platform height and platform distance accuracy can be within ±5 mm.
platform limit; close-range high angle; domain center algorithm; optimal transformation matrix
10.19713/j.cnki.43−1423/u.2019.03.031
U231+.4
A
1672 − 7029(2019)03 − 0796 − 08
2018−04−27
上海市科委重点支撑项目(16030501400);上海市科学技术委员会地方院校能力建设资助项目(14110501300)
何越磊(1972−),男,辽宁锦州人,教授,博士,从事轨道交通安全与检测技术方向研究;E−mail:hyldoc@163.com
(编辑 阳丽霞)
