分级加载下铁路路基粗粒土动力特性研究

李扬波，张家生, 2，朱志辉, 2，王晅, 2，石熊



分级加载下铁路路基粗粒土动力特性研究

李扬波1，张家生1, 2，朱志辉1, 2，王晅1, 2，石熊1

(1. 中南大学 土木工程学院，湖南 长沙 410075； 2. 中南大学 高速铁路建造技术国家工程实验室，湖南 长沙 410075)

利用大型动三轴试验仪对铁路路基粗粒土填料开展分级加载的循环三轴试验，分析围压、加载频率对粗粒土动应力-动应变关系、动弹模以及阻尼比等动力特性的影响。试验结果表明：随着围压或频率的增加，土体的动强度、动弹性模量和阻尼比均增大；动应变较小时频率或围压对阻尼比的影响较小，动应变较大时频率或围压对阻尼比影响较大。在试验基础上建立基于Hardin-Drnevich骨架曲线和符合广义Masing准则的粗粒土非线性动本构模型，并在ABAQUS中UMAT二次开发平台编制相应的子程序。通过与试验结果比较，验证了粗粒土非线性动本构模型的正确性。

粗粒土；大型动三轴试验；动弹性模量；阻尼比；二次开发

我国铁路建设发展迅速，高速铁路通车里程已居世界第一，在列车动力荷载作用下，铁路路基会产生沉降变形和翻浆冒泥等病害，影响铁路的安全运营。因此研究铁路路基填料在列车荷载作用下的动力特性对保障路基安全服役性能具有重要意义。Suiker等[1]研究了道砟及底砟的力学特性，得出循环荷载作用下试样的强度和刚度相对于静力试验会显著增加。Bian[2]研究了围压和动力幅值对道砟及底砟的轴向应变和体积应变等特性的影响。Trinh等[3]研究了含水率和饱和度对法国老铁路结构下受污染道砟层粗粒土试样的力学特性的影响，并建立了一个可考虑应力水平、循环次数和土体含水率等因素的本构模型。冷伍明等[4]研究了动应力幅值、含水率以及围压对粗粒土累计变形规律的影响，并提出了粗粒土动力变形稳定界限及判别标准。以上研究大多是针对铁路路基填料的静力特性及动力稳定性，关于动强度等动力特性方面的研究较少。路基中动应力传递规律对铁路路基设计具有重要指导意义，实测方式[5]是研究路基中动应力分布规律的主要手段，但现场实测具有受外界影响因素多、成本高昂和测点数目少等局限性，很难真实反映路基中动应力的时空变化规律。要正确评估列车荷载作用下路基中的动应力，有必要通过试验方法对铁路路基填料在动力荷载作用下的动弹性模量等动力特性的变化规律开展研究。岩土材料在动力荷载作用下表现出非线性和滞后性等动力特性，动弹性模量和阻尼比是反映土体非线性和滞后性的首要参数。土体动弹性模量和阻尼比研究已取得较丰硕的成果，如Hardin等[6]研究了粗粒土的最大剪切模量以及剪切模量随剪应变变化关系。Enomoto等[7]研究了未扰动级配良好粗粒土强度、变形特征及小应变特性。Cabalar[8]分析了砂土细粒含量与砂土动孔隙水压、动剪切模量和阻尼比等动力特性的关系。张希栋等[9]通过动三轴试验研究了黄土在双向动荷载作用下剪切模量影响因素，并采用修正Hardin模型描述了动剪切模量与动剪应变关系。陈乐求等[10]研究了干湿循环作用对化学改良泥质板岩粗粒土动弹性模量和阻尼比等力学特征参数的影响。粗粒土填料的动弹性模量和阻尼比是进行铁路路基动力响应分析的重要参数，对铁路路基设计具有重要意义，而目前关于铁路路基粗粒土填料动弹性模量及阻尼比等动力特性的研究较少，不能满足铁路路基动力设计的需求。土的非线性动力本构模型是反映土体动力特性的最基本关系[11]，然而商业软件中缺少土体动力本构模型，无法合理反映动力荷载作用下土体动力特性，在商业软件中对动力本构模型进行二次开发，是解决该问题的有效途 径[11−13]。铁路路基粗粒土填料动力本构模型研究较少，特别是模拟铁路路基动力响应时，通常使用Drucker-Prager等静力本构[14−15]，与列车荷载作用下土体实际动力响应特征相差较大。综上所述，目前对列车荷载作用下路基粗粒土填料动力响应规律的认识仍较模糊，有待进一步研究。本文以铁路路基粗粒土填料为试验材料，通过大型动三轴试验仪，分析围压、荷载频率对粗粒土动应力−动应变关系、动弹性模量以及阻尼比等动力特性的影响。基于试验结果建立基于Hardin-Drnevich骨架曲线和符合广义Masing准则的粗粒土非线性动本构模型，并在ABAQUS中编制了相应的粗粒土非线性动本构模型子程序。

1 试验方案

1.1 试验仪器及试验材料

采用TAJ-2000大型动静三轴试验仪对粗粒土试样开展动力特性试验，该仪器由主机、油压源系统以及电控系统组成，主机构造如图1所示。该仪器能实现应变控制、应变速率控制和应力控制3种控制方式，能施加环向和轴向动静力荷载。数据采集系统能采集动应力、动应变、动孔隙水压力以及体变等数据。试样尺寸为直径300 mm、高600 mm。

试验所用原始粗粒土填料为长沙市南郊公园附近的细角砾土，粗颗粒为青灰色砂岩，采用碎石对原始填料进行改良，按50:50的质量比例配成试验土样，符合《铁路路基设计规范》[16]中规定的粗粒土B组填料。通过筛分试验，获得试样的级配曲线如图2所示，试样最大粒径约为60 mm，由DJ30-5重型电动击实仪进行击实试验，获得试样的物理指标如表1所示。

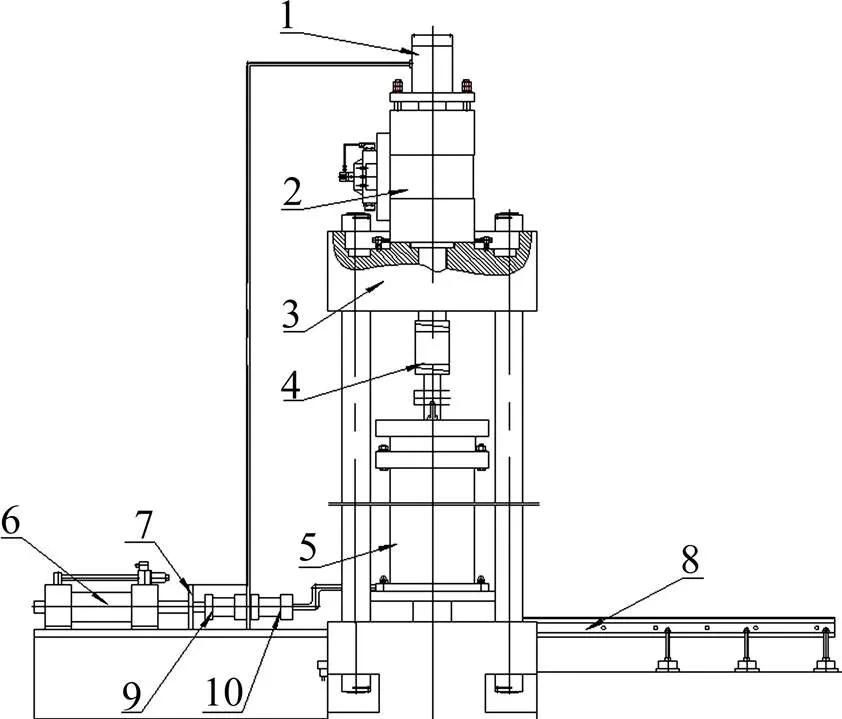
1—串联水缸；2—轴向液压缸；3—机架；4—负荷传感器；5—三轴压力室；6—侧向液压缸；7—侧向水缸；8—导航；9—反压液压缸；10—反压水缸

表1 试样的物理参数

图2 试样级配曲线

1.2 试验方案

试验严格按照《铁路工程土工试验规范》中相关规定开展[17]，试验分为制样、饱和、固结和加载4个步骤。根据相关规定[16]，压实系数控制在0.97，为保证压实效果，分5层对试验土样进行击实，每层击实后对表面进行刮毛；试样采用真空抽气法从下而上进行饱和，当上部出水20 min后，改用水头饱和法进行饱和，当孔压力系数达到0.95后饱和完成；采用双向排水等压固结，逐级对试样施加轴向和侧向压力直至达到固结围压，同时监测试样的排水量，固结完成的标志为试样在30 min内排水量小于15 mL；为研究不同动应力幅值下试样的动力特性，采用应力控制式加载方法，每个试样进行分级加载试验，每级加载试验施加相同幅值的循环荷载6次，试验时逐级改变动荷载幅值，初始动荷载幅值取围压的0.1倍，然后每级动荷载幅值增加围压的0.1倍，如图3所示，当应变波形明显发散时结束加载。

图3 试验加载曲线

铁路路基动应力实测数据表明[4]，在列车荷载作用下路基动应力呈现明显的周期效应，因此本次试验采用正弦波循环荷载加载。列车荷载作用对路基影响最大的频率等于列车运行速度除以车厢长度，取每节车厢长度为25 m，本试验加载频率取1，3和5 Hz，分别对应列车运行时速为90，270和450 km时对路基的作用频率。试验围压分别为200，300和400 kPa，考虑到列车荷载作用在路基的时间很短暂，采用不排水三轴试验，共开展9组试验。

2 试验结果分析

2.1 骨架曲线

试验得到试样在不同幅值动力荷载作用下动应力−动应变滞回曲线，取动应力−动应变滞回曲线顶点处对应的动应力和动应变，得到反映动应力−动应变非线性的骨架曲线，计算时统一取每级动荷载幅值下第3个循环的动应力−动应变滞回曲线为依据。图4所示为相同围压下加载频率对试样骨架曲线的影响。

(a) 围压200 kPa；(b) 围压300 kPa；(c) 围压400 kPa

由图4可知，粗粒土试样动应力−动应变关系呈现出明显的非线性特征，且具有应变硬化的趋势。当动应变较小时，试样动应力−动应变近似为线性关系，即在此应变量级下，试样呈现出近似弹性特性；随着动应变的增大，土体非线性特征越来越明显。从图中可知，围压一定时，加载频率越大，试样的动应力−动应变骨架曲线就越高，说明在相同围压下，试样的动强度随着加载频率的增加而增加，粗粒土试样骨架曲线的变化规律与频率成正相关性。粗粒土试样压实度要求较高，但颗粒之间仍然存在孔隙，SUN等[18]指出不同频率荷载作用下不同粒径颗粒的响应程度不同，较细的颗粒在较高频率荷载的作用下更易产生响应而进行重新排列，在不引起颗粒破碎的情况下粗粒土试样强度主要与土颗粒间的重新排列有关[19]。因此，在较高频率荷载作用下，细颗粒能更好的填充在大颗粒之间的孔隙中，使颗粒排列更密实，从而提高土体强度，即试样的动强度随着加载频率的增加而增加。

2.2 动弹性模量

在动荷载作用下，土体内部产生的动应力和动应变响应均为时间的函数，而其弹性模量在动荷载作用下不是固定的，动弹性模量取每级荷载下动应力−动应变滞回圈顶点与原点连线的斜率，表达 式为：

式中：d和d分别为各时刻对应的动应力和动应变。

通过式(1)求得不同动应变下试样的动弹性模量，如图5所示。可知，动应变较小时，动弹性模量随着动应变的增大急剧减小，该阶段土体由弹性状态逐渐向弹塑性状态转变；随着动应变的增大，动弹性模量衰减变慢，因为该阶段土体以塑性变形为主，动弹性模量逐渐趋于稳定。图5(a)为围压等于300 kPa时，不同加载频率条件下粗粒土试样动弹性模量随动应变变化规律。可知在相同围压下，粗粒土试样的动弹性模量随着作用荷载频率的增大而增大。图5(b)所示为荷载频率等于3 Hz时，不同围压下粗粒土试样动弹性模量随动应变变化规律，可知在相同作用频率下，粗粒土试样的动弹性模量随着围压的增大而增大，由于围压增大导致试样土体颗粒接触更紧密，试样刚度增大，即试样的动弹性模量随着围压的增大而增大。由此可知，粗粒土试样的动弹性模量与频率和围压均成正相 关性。

2.3 阻尼比

在周期荷载作用下，土体发生变形时内部阻力消耗能量的性质可用阻尼比反映，其体现了土体动应变相对于动应力的滞后特性，是反映土体动力特性的重要指标。土的阻尼比可用如下公式表示：

其中：Δ为一个周期内损耗的能量；为作用的总能量。如图6所示，土体损耗能量可用滞回曲线所围面积的1/4表示，而1个周期内动荷载作用的总能量等于原点到最大幅值点连线下的三角形面积，即图6中阴影部分面积。

(a) 围压300 kPa；(b) 频率3 Hz

图5 动弹性模量与动应变关系曲线

Fig. 5 Relation curves of dynamic elastic modulus and dynamic strain

图6 滞回曲线

(a) 围压300 kPa；(b) 频率3 Hz

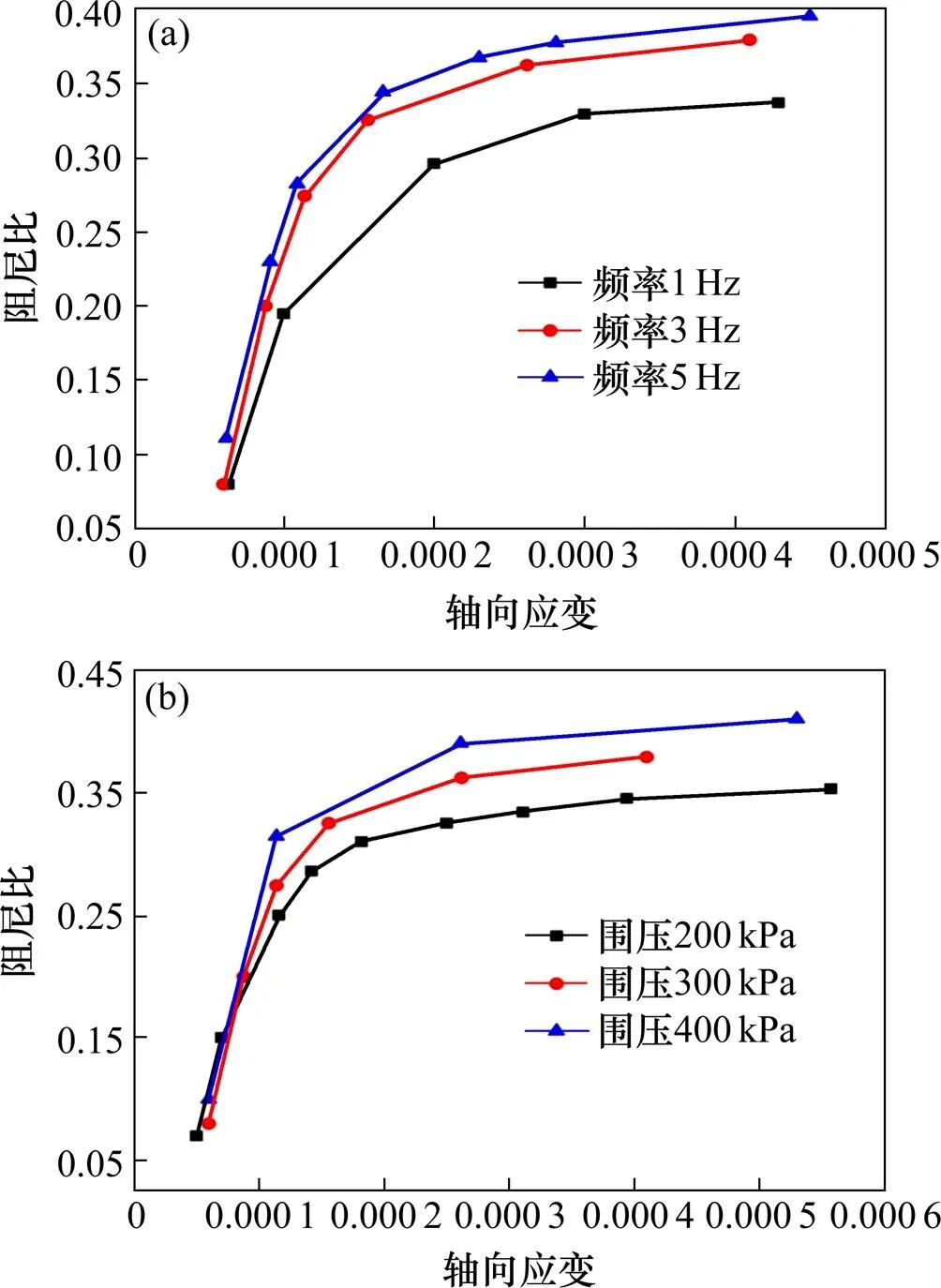
利用式(2)可求得粗粒土试样不同动应变下的阻尼比，如图7所示。可知在动应变位于10-4~10-3范围内粗粒土试样的阻尼比随动应变增大而增大，非线性特征明显。在该应变范围内阻尼比呈现急剧增长−缓慢增长−趋于平缓的过程，即在动应变较小时，阻尼比随着动应变的增大而急剧增大，随着动应变继续增大，阻尼比增长逐渐变慢，最后趋于平缓。随着动应变的增大，即随着动力加载幅值的增大，土体结构逐渐发生破坏，土颗粒间产生相互翻越、错动和滚爬等行为，导致动力波在穿越土体时消耗更大能量，最终表现为阻尼比随着动应变的增大而增大。图7(a)所示为围压相同时加载频率对试样阻尼比与轴向应变关系曲线的影响。可知相同应变下试样的阻尼比随着加载频率增大而增大，在动应变较小时，频率对阻尼比的影响较小，动应变较大时，频率对阻尼比的影响较大。图7(b)所示为加载频率相同时围压对试样阻尼比与轴向应变关系曲线的影响。动应变较小时，围压对粗粒土试样阻尼比的影响不明显，但应变较大时，粗粒土试样的阻尼比呈现出随着围压增大而增大的趋势。

3 粗粒土动本构模型

3.1 粗粒土动本构及二次开发

由图4可知，粗粒土试样动应力−动应变骨架曲线近似为双曲线，因此采用如式(3)所示的Hardin- Drnevich双曲线模型对粗粒土动应力−动应变骨架曲线进行描述。

式中：max为轴向最大动弹性模量；max为轴向最大动应力。

弹性压缩模量和弹性剪切模量可由下式进行转换：

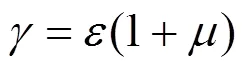
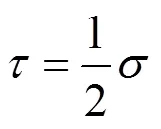
则Hardin-Drnevich双曲线模型可写成：

式中：d为动剪应力；r为参考剪应变；d为动剪应变；0为初始剪切模量。

初始剪切模量0为[20]：

式中：a为大气压力；和为试验参数；′为平均有效主应力。

参考剪应变表达式为：

y可由摩尔−库伦破坏理论求得：

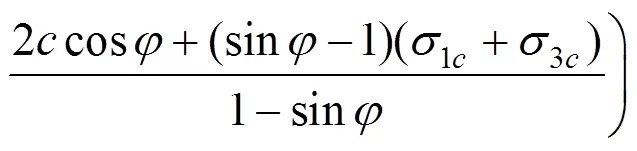
式中：1和3表示主应力；为黏聚力；为内摩擦角；1c为轴向固结压力；3c为侧向固结压力。

Masing准则认为骨架曲线和滞回曲线中加载曲线及卸载曲线的形状均一致，而动应力−动应变滞回曲线坐标比尺是骨架曲线的2倍，且剪切模量在加卸载转变后的瞬时等于初始最大剪切模量0，则粗粒土非线性动本构滞回曲线的表达式为：

根据式(7)对等号两边同时对应变求偏导，可得在骨架曲线上任意时刻对应的剪切模量为：

同理，通过对式(11)等号两边同时对应变求偏导，则任意时刻下滞回曲线上的剪切模量可表 示为：

式中：dm为滞回曲线加卸载转折点对应的剪应变。

如式(13)所示，加卸载的判断将影响剪切模量的取值，在对土体开展三维动力非线性分析时，可采用八面体应力−应变关系表示土的应力−应变关系[12]，本文选择以八面体剪应变来判定土体的加卸载状况：

式中：0表示八面体剪应变；1，2和3表示主 应变。

则是否发生加载或者卸载的判断方式为：

式中：Δ0为任意时刻增量下的土体应变增量；γ表示当前八面体剪应变。

土的三维黏弹性模型为：

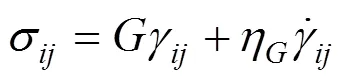
式中：为土体体积模量；为剪切模量；η为体积黏滞系数；η为剪切黏滞系数；ε为体积应变；ε为应变偏量。

采用中心差分法推导雅克比矩阵，其通项表达式如下：

式中：为时间；为任意可导函数。

将式(16)结合中心差分法写成增量形式：

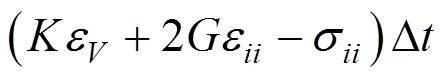
两边分别对Δε和Δε求偏导，得：

同理对式(17)进行变换，可得：

由此可得到雅克比矩阵，根据以上分析，在ABAQUS中的UMAT二次开发平台上编写了粗粒土非线性动本构模型子程序。

3.2 程序验证

为验证本文开发的粗粒土非线性动本构模型子程序的正确性，将其应用在图8所示的数值模型中，与试验结果进行比较。模型直径300 mm，高600 mm，加载时在上部施加分级循环动力荷载，加载方式与三轴试验加载方式一致。由式(7)可知粗粒土非线性动本构模型包含2个试验参数，其中初始剪切模量0取值如表2所示，参考剪应变r在围压为200，300和400 kPa时的取值分别0.000 35，0.000 4和0.000 43。

表2 初始剪切模量

图8 数值模型

(a) 围压200 kPa；(b) 围压300 kPa；(c) 围压400 kPa

图9所示为试验数据与数值模拟结果得到的动弹性模量对比。可知本文模拟结果与试验结果吻合较好，粗粒土非线性动本构能较好的模拟弹性模量随轴向应变的变化趋势，说明本文开发的粗粒土非线性动本构模型可较好的反映动力荷载作用下粗粒土填料的非线性特征。表明本文所开发粗粒土非线性动本构模型的正确性，可为列车重复荷载作用下铁路路基动力响应数值模拟提供动力本构模型。

4 结论

1) 粗粒土试样的动应力-动应变骨架曲线呈现出非线性特征，且具有应变硬化的趋势；频率越大，试样的骨架曲线就越高，即试样的动强度越大。

2) 粗粒土试样的动弹性模量随着荷载作用频率的增加而增加，随着围压的增大而增大，粗粒土试样的动弹性模量与频率和围压均成正相关性。

3) 粗粒土试样的阻尼比随着加载频率增大而增大；在动应变较小时，频率和围压对阻尼比的影响较小；动应变较大时，频率和围压对阻尼比的影响较大。

4) 推导了三维空间下基于Hardin-Drnevich骨架曲线和符合广义Masing准则的粗粒土非线性动本构模型，并开发了相应的子程序。通过试验结果比较，验证了该本构模型的正确性，试图为列车荷载作用下铁路路基动力响应数值模拟提供合理的动力本构模型。

[1] Suiker A A, Selig E T, Frenkel R. Static and cyclic triaxial testing of ballast and subballast[J]. Journal of Geotechnical and Geoenvironmental Engineering (ASCE), 2005, 131(6): 771−782.

[2] Bian. Cyclic and postcyclic triaxial testing of ballast and subballast[J]. Journal of Materials in Civil Engineering (ASCE), 2016, 28(7): 1−11.

[3] Trinh V N, Tang A M, Cui Y, et al. Mechanical characterisation of the fouled ballast in ancient railway track substructure by large-scale triaxial tests[J]. Soils and Foundations, 2012, 52(3): 511−523.

[4] 冷伍明, 刘文劼, 赵春彦, 等. 重载铁路路基压实粗颗粒土填料动力破坏规律试验研究[J]. 岩土力学, 2015, 36(3): 640−646. LENG Wuming, LIU Wenjie, ZHAO Chunyan, et al. Experimental research on dynamic failure rules of compacted coarse-grained soil filling in heavy haul railway subgrade[J]. Rock and Soil Mechanics, 2015, 36(3): 640−646.

[5] 郭志广, 魏丽敏, 何群, 等. 武广高速铁路无砟轨道路基动力响应试验研究[J]. 振动与冲击, 2013, 32(14): 148−152. GUO Zhiguang, WEI Limin, HE Qun, et al. Tests for dynamic response of ballastless track subgrade of Wu-Guang high-speed railway[J]. Journal of Vibration and Shock, 2013, 32(14): 148−163.

[6] Hardin B O, Kalinski M E. Estimating the shear modulus of gravelly soils[J]. Journal of Geotechnical and Geoenvironmental Engineering (ASCE), 2005, 131(7): 867−875.

[7] Enomoto T, Hassan Qureshi O, Sato T, et al. Strength and deformation characteristics and small strain properties of undisturbed gravelly soils[J]. Soils and Foundations, 2013, 53(6): 951−965.

[8] Cabalar A F. Applications of the oedometer, triaxial and resonant column tests to the study of micaceous sands[J]. Engineering Geology, 2010, 112(1/4): 21−28.

[9] 张希栋, 骆亚生. 双向动荷载下黄土的动剪切模量特性研究[J]. 岩土力学, 2015, 36(9): 2591−2598. ZHANG Xidong, LUO Yasheng. Study of dynamic shear modulus of loess under bidirectional dynamic loads[J]. Rock and Soil Mechanics, 2015, 36(9): 2591−2598.

[10] 陈乐求, 陈俊桦, 张家生. 干湿循环作用下水泥改良泥质板岩粗粒土动力特性[J]. 湖南大学学报(自然科学版), 2017, 44(9): 107−113. CHEN Leqiu, CHEN Junhua, ZHANG Jiasheng. Dynamic properties of cement-improved argillite-slate coarse-grained soil under drying-wetting cycles[J]. Journal of Hunan University (Natural Sciences), 2017, 44(9): 107−113.

[11] 张如林, 楼梦麟. 基于达维坚科夫骨架曲线的软土非线性动力本构模型研究[J]. 岩土力学, 2012, 33(9): 2588−2594. ZHANG Rulin, LOU Menglin. Study of nonlinear dynamic constitutive model of soft soil based on davidenkov skeleton curve[J]. Rock and Soil Mechanics, 2012, 33(9): 2588−2594.

[12] 胡勤, 戚承志. Ramberg-Osgood土动力非线性模型在ABAQUS软件上的开发及应用[J]. 岩土力学, 2012, 33(4): 1268−1274. HU Qin, QI Chengzhi. Development and application of Ramberg-osgood soil dynamic nonlinear constitutive model on ABAQUS code[J]. Rock and Soil Mechanics, 2012, 33(4): 1268−1274.

[13] 邹炎, 景立平, 崔杰, 等. 基于Hardin曲线的土体边界面本构模型在ADINA软件中的实现[J]. 岩土力学, 2015, 36(1): 75−82. ZOU Yan, JING Liping, CUI Jie, et al. Hardin curve based boundary surface constitutive model of soil and implementation in ADINA software[J]. Rock and Soil Mechanics, 2015, 36(1): 75−82.

[14] 薛富春, 张建民. 移动荷载作用下高速铁路路基动应力的空间分布[J]. 铁道学报, 2016, 38(1): 86−91. XUE Fuchun, ZHANG Jianmin. Spatial distribution of dynamic stresses in embankment of high-speed railway under moving loads[J]. Journal of the China Railway Society, 2016(1): 86−91.

[15] 杜衍庆, 白明洲, 倪守睿. 列车相向运行对双线无砟轨道高速铁路路基动应力响应分析[J]. 北京工业大学学报, 2014, 40(4): 580−585. DU Yanqing, BAI Mingzhou, NI Shourui. Analysis of the subgrade dynamic stress under the trains opposite running on double-rack high-speed railway[J]. Journal of Beijing University of Technology, 2014, 40(4): 580−585.

[16] TB 10001—2016, 铁路路基设计规范[S].TB 10001—2016, Code for design on subgrade of railway[S].

[17] TB 10102—2010, 铁路工程土工试验规程[S]. TB 10102—2010, Code for soil test of railway engineering[S].

[18] SUN Q D, Indraratna B, Nimbalkar S. Deformation and degradation mechanisms of railway ballast under high frequency cyclic loading[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2016, 142(1): 1−12.

[19] 蔡袁强, 赵莉, 曹志刚, 等. 不同频率循环荷载下公路路基粗粒填料长期动力特性试验研究[J]. 岩石力学与工程学报, 2017, 36(5): 1238−1246. CAI Yuanqiang, ZHAO Li, CAO Zhigang, et al. Experimental study on dynamic characteristics of unbound granular materials under cyclic loading with different frequencies[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(5): 1238−1246.

[20] 谢定义. 土动力学[M]. 北京: 高等教育出版社, 2011. XIE Dingyi. Soil dynamics[M]. Beijing: High Education Press, 2011.

Study on dynamic characteristics of coarse grained soil filler in railway subgrade under stepped axial cyclic loading

LI Yangbo1,ZHANG Jiasheng1, 2, ZHU Zhihui1, 2,WANG Xuan1, 2, SHI Xiong1

(1. School of Civil Engineering, Central South University, Changsha 410075, China; 2. National Engineering Laboratory for High Speed Railway Construction, Central South University, Changsha 410075, China)

A large scale dynamic triaxial test apparatus was used to carry out cyclic triaxial tests on Railway Subgrade coarse grained soil fillers. The effects of confining pressure and loading frequency on the dynamic stress-strain relationship, dynamic modulus and damping ratio of coarse grained soil were analyzed. The experimental results show that with the increase of confining pressure or frequency, the dynamic strength, dynamic elastic modulus and damping ratio of the soil increase. When the dynamic strain is small, the influence of frequency or confining pressure on damping ratio is relatively small, and the larger the dynamic strain is, the greater the impact is. On the basis of experiments, a dynamic nonlinear constitutive model of coarse grained soil based on Hardin-Drnevich skeleton curve and generalized Masing criterion is established, and the corresponding subroutine (UMAT) is compiled on the secondary development platform of ABAQUS. The correctness of the dynamic nonlinear constitutive model of coarse-grained soil is verified by comparison with the experimental results.

coarse grained soil; large scale dynamic triaxial tests; dynamic modulus; damping ratio; secondary development

10.19713/j.cnki.43−1423/u.2019.03.009

TU44

A

1672 − 7029(2019)03 − 0620 − 09

2018−04−26

国家自然科学基金资助项目(51678576，51378514)

石熊(1985−)，男，湖南邵阳人，博士，从事路基动力学研究；E−mail：shixiong126@126.com

(编辑 涂鹏)