考虑梁柱节点黏结−滑移模型的混凝土框架滞回性能研究

2019-04-16唐昌辉黄超淼

铁道科学与工程学报 2019年3期

唐昌辉，黄超淼

唐昌辉，黄超淼

(湖南大学土木工程学院，湖南长沙 410082)

基于有限元软件OpenSEES中已有的梁柱宏观柔性节点单元和梁柱纵筋黏结滑移模型，对国内研究者已经完成的钢筋混凝土框架以及型钢混凝土框架水平低周往复荷载试验得到的滞回曲线、位移延性、滞回面积以及耗能能力等滞回性能进行有限元模拟分析，并与试验结果进行比对。根据有限元模拟结果建立基于OpenSEES软件的钢筋混凝土框架和型钢混凝土框架考虑梁柱宏观柔性节点的计算模型,为钢筋混凝土框架和型钢混凝土框架的设计计算提供一条有效途径。

型钢混凝土框架；宏观柔性节点模型；OpenSEES；滞回曲线；黏结滑移

由于计算机应用的飞速发展，建筑结构分析变得越来越快捷，复杂的运算和存储可由计算机来完成，计算模型的建立就显得尤为重要。目前，混凝土框架的分析模型主要有基于材料本构层面的纤维模型[1−3]。伍永飞等[4]利用弹塑性纤维模型来模拟梁柱单元。Taucer等[5]采用纤维梁柱单元对钢筋混凝框架结构在地震作用下的响应进行了模拟。吕西林等[6]基于纤维模型并结合分段刚度概念推导建立了便于框架结构非线性分析应用的纤维杆元模型。在框架结构中，混凝土梁柱节点的强度损伤和刚度下降都对整个结构的性能有着重大影响。但在以往的有限元分析方法中，节点的这些影响很少考虑，在模拟混凝土框架非弹性反应的作用时，梁柱节点都被视为刚性，通常通过在框架结构的梁柱单元中加入塑性铰来考虑梁柱节点的非弹性反应[7−8]。此方法能够在一定程度上描述节点的受力特性，但是它不能考虑节点的剪切变形以及节点区内钢筋的黏结滑移带来的影响，因此不能很好地反映地震作用下框架结构真实的受力和变形情况。为此，本文针对这一问题，从考虑梁柱宏观柔性节点的混凝土框架有限元模型出发，利用OpenSEES有限元软件中已有的梁柱宏观柔性节点单元和梁柱纵筋黏结滑移模型，对国内研究者已经完成的低周往复荷载作用下的钢筋混凝土框架以及型钢混凝土框架的滞回性能进行分析，并与试验数据进行比较，获得的结论可为混凝土框架在进行整体结构的非弹性分析时有必要考虑宏观柔性节点模型提供理论依据与支撑。

1 混凝土框架有限元模型的建立

OpenSEES是由加州大学伯克利分校和太平洋地震工程研究中心共同开发的一款开源且有强大非线性模拟能力的有限元非线性分析软件，具有效率高、精度高的特点。本文基于OpenSEES有限元软件已有的梁柱节点单元[9−13]，建立考虑梁柱宏观柔性节点的钢筋混凝土和型钢混凝土框架有限元模型。

框架的梁和柱均采用基于柔度法的非线性梁柱单元(nonlinear Beam Column)，整体有限元模型如图1所示。单元中的混凝土材料采用能够考虑刚度退化和箍筋约束作用的Kent-Scott-Park模型；钢筋材料采用基于Giuffre-Menegotto-Pinto的本构模型；单元截面则采用由混凝土纤维和钢筋纤维组成的纤维截面模型。

基于朱孝辉等[14]对混凝土框架节点滞回性能的研究，宏观柔性节点模型采用由Lowes等[15−17]提出，并由Mitra[18]改进的节点模型，该模型采用3种元件模拟节点的3种破坏机制：即用1个剪切板元件(Shear panel component)来模拟由于节点核心区剪切失效引起的强度和刚度的退化；8个0长度的钢筋滑移弹簧元件(Bar-slip component)来模拟梁柱纵筋在节点区的黏结退化引起的节点强度和刚度的退化；4个0宽度的交界面剪切弹簧元件(Interface-shear component)来模拟节点与梁柱交界处的传递剪力能力的退化。

图1 考虑梁柱宏观柔性节点的框架有限元模型

同时，采用刚性节点假定，即不考虑梁柱宏观柔性节点模型对钢筋混凝土框架结构进行建模，建立的非线性数值模型与考虑梁柱宏观柔性节点模型的框架有限元模型对比，整体有限元模型如图2所示。梁柱单元采用易于收敛的塑性铰单元(beam With Hinges)，单元中的混凝土材料仍采用能够考虑刚度退化和箍筋约束作用的Kent-Scott-Park模型；钢筋材料采用基Giuffre-Menegotto-Pinto的本构模型；截面也仍采用纤维截面模型。

图2 不考虑梁柱宏观柔性节点的框架有限元模型

2 混凝土框架滞回性能研究

2.1 试验概况

选取张鹏[19]完成的两榀混凝土框架F30和F50进行有限元非线性分析，以验证运用OpenSEES中的宏观柔性节点模型对混凝土框架进行非线性分析的可靠性，并对比考虑宏观柔性节点与不考虑宏观柔性节点(刚性节点假定)时的计算结果。

试验在同济大学土木工程防灾国家重点实验室完成。混凝土和钢筋的实测力学性能分别如表1和表2所示。

表1 混凝土的力学性能

表2 钢筋的力学性能

2.2 试验结果及有限元模拟分析

图3(a)和图4(a)分别为框架F30和F50考虑宏观柔性节点模型时混凝土框架荷载−位移滞回曲线的模拟和试验的对比结果，图5(a)和图6(a)分别为框架F30和F50考虑宏观柔性节点模型时混凝土框架骨架曲线的模拟和试验对比结果；图3(b)和图4(b)分别为框架F30和F50不考虑宏观柔性节点模型时混凝土框架荷载−位移滞回曲线的模拟和试验的对比结果，图5(b)和图6(b)分别为框架F30和F50不考虑宏观柔性节点模型时混凝土框架骨架曲线的模拟和试验对比结果。从图5可以看出，考虑宏观柔性节点模型计算的混凝土框架荷载−位移滞回曲线和骨架曲线与试验测得的混凝土框架实际的荷载−位移滞回曲线和骨架曲线吻合良好。

(a)考虑宏观柔性节点模型；(b)不考虑宏观柔性节点模型

考虑宏观柔性节点模型时混凝土框架荷载−位移滞回曲线，在卸载和反向加载时，较好地体现了节点区混凝土的剪切变形和纵筋的黏结滑移特性引起的刚度退化和捏缩效应，能较好地模拟框架滞回曲线的捏拢现象。不考虑宏观柔性节点模型时混凝土框架的荷载−位移滞回曲线在卸载和反向加载时曲线的刚度退化和捏缩效应均不明显，不能很好地模拟框架滞回曲线的捏拢现象。

考虑宏观柔性节点模型时混凝土框架荷载−位移骨架曲线的模拟和试验结果吻合良好，而不考虑宏观柔性节点模型(刚性节点假定)的混凝土框架在正向加载时的承载力高于混凝土框架通过试验测得的实际承载力，结构的刚度和强度退化均不明显，不能很好的反映由于节点核心区剪切失效和黏结滑移引起的强度退化和刚度退化。

表3 框架的抗侧承载力

框架F30和F50的抗侧承载力max，位移延性系数f以及与耗能相关的滞回阻尼系数e的试验值与按考虑宏观柔性节点模型的有限元模拟计算值均分别见表3 和表4。从表3和表4可以看出，根据有限元模拟得到的各项数值的计算值与试验值吻合良好。框架F30和F50在低周反复水平荷载作用下的滞回阻尼系数e实测值分别为0.160和0.224，延性系数f分别为3.91和4.45，框架表现出良好的滞回延性性能。

表4 框架的位移延性与耗能

3 型钢混凝土框架滞回性能研究

3.1 试验概况

唐昌辉[20]完成了三榀型钢混凝土柱组合框架KJ-2，KJ-3和KJ-4的低周反复水平荷载试验并进行有限元非线性分析。试验在工程结构损伤诊断湖南省重点实验室的SCHEHCK电液伺服系统上进行，框架基本数据如表5所示，钢材的力学指标如表6所示。

表5 框架试验基本数据

表6 钢材力学性能指标

3.2 试验结果及有限元模拟分析

运用OpenSEES中的宏观柔性节点模型对型钢混凝土框架进行非线性分析，与实验结果进行比对以验证模型的可靠性。分析时型钢混凝土梁柱单元选用基于柔度法的非线性梁柱单元(nonlinear Beam Column)，截面采用由混凝土纤维和钢筋纤维组成纤维截面，其中型钢混凝土柱纤维截面图如图7所示。单元中材料的选取以及节点模型的选取则与普通混凝土框架一致。

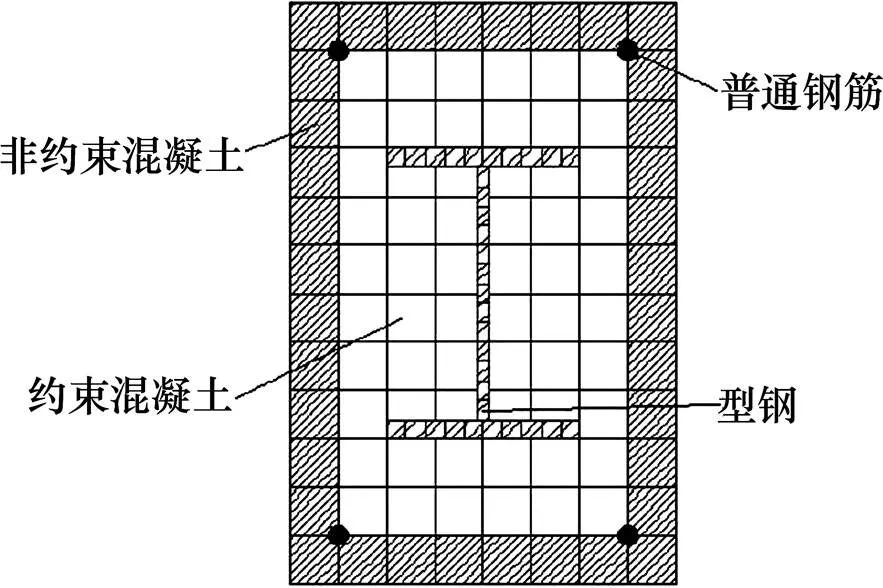
图7 型钢混凝土柱纤维截面

图8~10分别为型钢混凝土框架KJ-2，KJ-3和KJ-4考虑宏观柔性节点模型时荷载-位移滞回曲线和骨架曲线的模拟和试验对比结果，从图中可以看出，模拟的结果与试验结果符合良好。

考虑宏观柔性节点模型计算的滞回曲线在卸载和反向加载时，能较好地模拟了节点区混凝土的剪切变形和纵筋的黏结滑移特性，并较好地模拟框架滞回曲线的滞回规则。图8~10中三榀框架的滞回曲线均较为饱满，滞回耗能较大，结构延性较好，且随着柱轴压比越低“捏缩”现象越不明显，滞回曲线越饱满，延性越好。同样三榀框架反向加载滞回曲线的丰满程度比正向好，在同一加载控制阶段反向荷载和位移均大于正向。

考虑宏观柔性节点模型的型钢混凝土框架荷载−位移骨架曲线存在明显的特征点，骨架曲线在开裂点、钢筋屈服点和峰值点表现出明显的弯折，特别是曲线过了峰值点后，荷载−挠度骨架曲线平缓下降，表明型钢的存在使得构件此时仍具有一定的承载力。

表7 框架的抗侧承载力

三榀框架的抗侧承载力max，位移延性系数f以及与耗能相关的滞回阻尼系数e的试验值与计算模拟值见表7~8。从表7和表8可以看出，各项数值的计算模拟值与试验值符合良好。组合框架在低周反复水平荷载作用下的滞回阻尼系数e实测值为0.164~0.278，延性系数f为2.51~3.34，框架表现出良好的滞回延性性能。

表8 框架的位移延性与耗能

(a) KJ-2的荷载−位移滞回曲线；(b) KJ-2的荷载−位移骨架曲线

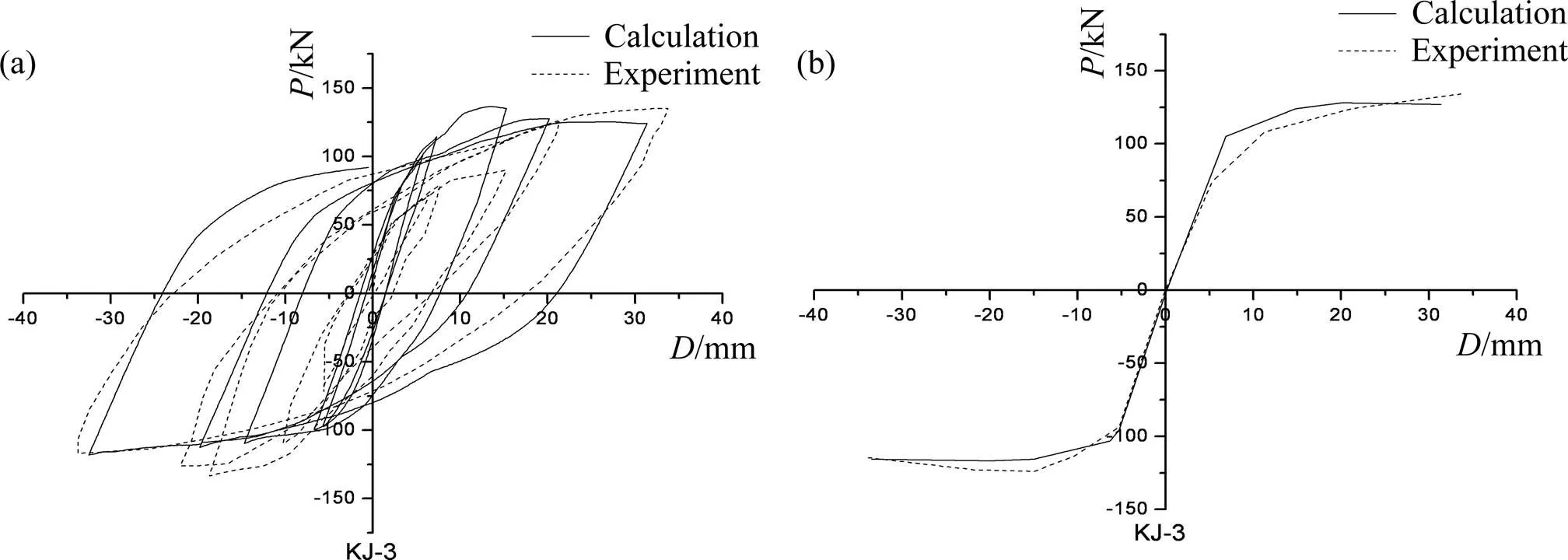
(a) KJ-3的荷载−位移滞回曲线；(b) KJ-3的荷载−位移骨架曲线

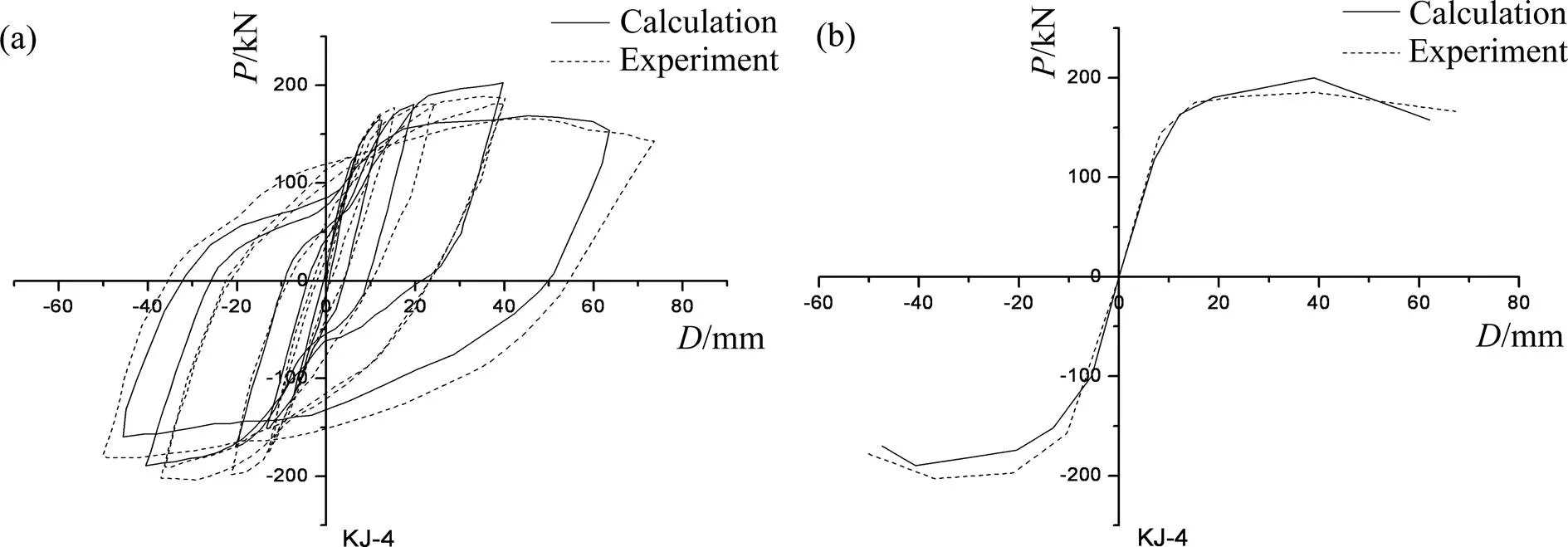
(a) KJ-4的荷载−位移滞回曲线；(b) KJ-4的荷载−位移骨架曲线

4 结论

1) 基于OpenSEES软件，对两榀钢筋混凝土框架以及三榀型钢混凝土框架分别建立了考虑宏观柔性节点的计算模型。

2) 模拟结果表明，考虑宏观柔性节点模型计算的钢筋混凝土框架以及型钢混凝土框架荷载−位移滞回曲线以及骨架曲线与试验测得的滞回曲线和骨架曲线吻合良好，在卸载和反向加载时，较好地体现了节点区混凝土的剪切变形和纵筋的黏结滑移特性引起的刚度退化和捏缩效应。

3) 基于混凝土框架有限元模型得到的钢筋混凝土框架及型钢混凝土框架抗侧承载力、位移延性以及耗能的计算值均与试验值吻合良好，说明Open SEES能够较好地模拟混凝土框架的受力全过程。

[1] 张强, 周德源, 伍永飞, 等. 钢筋混凝土框架结构非线性分析纤维模型研究[J]. 结构工程师, 2008, 24(1): 15−20. ZHANG Qiang, ZHOU Deyuan, WU Yongfei, et al. Research on nonlinear analysis fiber model of reinforced concrete frame structure[J]. Structural Engineer, 2008, 24(1): 15−20.

[2] 宁超列. 基于纤维铰模型的框架结构非线性地震反应分析[D]. 哈尔滨: 哈尔滨工业大学, 2008.NING Chaolie. Nonlinear seismic response analysis of frame structure based on fiber hinge model[D]. Harbin: Harbin Institute of Technology, 2008.

[3] 伍永飞, 周德源. 纤维模型在平面框架非线性静力分析中的应用[J]. 东南大学学报(自然科学版), 2005(增1): 129−132. WU Yongfei, ZHOU Deyuan. Application of fiber models in nonlinear static analysis of plane frames[J]. Journal of Southeast University (Natural Science Edition), 2005 (Suppl 1): 129−132.

[4] 伍永飞. 钢筋混凝土框架结构静力非线牲分析程序研制[D].上海: 同济大学, 2007.WU Yongfei. Development of analytical program for static non-linear accommodate of reinforced concrete frame structures[D]. Shanghai: Tongji University, 2007.

[5] Taucer F F, Spacone E, Fillippou F C. A fiber beam-column element for seismic response analysis of reinforced concrete structures[R]. Report No. UCB/ EERC-91/17, University of California at Berkeley, CA, 1991.

[6] 吕西林, 卢文生. 纤维杆元模型在框架结构非线性分析中的应用[J].力学季刊, 2006, 27(1): 14−22. LÜ Xilin, LU Wensheng. Application of fiber bar element model in nonlinear analysis of frame structures[J]. The Quarterly of Mechanics, 2006, 27(1): 14−22.

[7] 陈明政. 预应力混凝土框架塑性内力重分布与弯矩调幅的研究[D]. 重庆: 重庆大学, 2006. CHEN Mingzheng. Research on the redistribution of plasticity and bending moment in prestressed concrete frame[D]. Chongqing: Chongqing University, 2006.

[8] 徐伟良, 吴德伦. 钢筋混凝土框架全过程分析的非线性简化单元及其应用[J]. 建筑结构学报, 1995(3): 59− 65.XU Weiliang, WU Delun. Nonlinear simplified element analysis and application of entire process analysis of reinforced concrete frame[J]. Journal of Building Structures, 1995(3): 59−65.

[9] Biddah A, Ghobarah A. Modeling of shear deformation and bond slip in reinforced concrete joints[J]. Structural Engineering and Mechanics, 1999, 7(4): 413−432.

[10] Yousssef M, Ghobarah A. Modeling of RC beam-column joints and structural walls[J]. Journal of Earthquake Engineering, 2001, 5(1): 93−111.

[11] Lowe L N, Altoontash A. A beam-column joint element [R]. PEER Report, 2003.

[12] Mitra N, Lowes L. Evaluation, calibration and verification of a reinforced concrete beam-column joint model[J]. Journal of Structural Engineering, 2007, 133(1): 105−120.

[13] 傅剑平. 钢筋混凝土框架节点抗震性能与设计方法研究[D]. 重庆: 重庆大学, 2002. FU Jianping. Seismie behaviour and design of joints in a reinforeed conerete frame[D]. Chongqing: Chongqing University, 2002.

[14] 朱孝辉. 混凝土框架节点滞回性能研究[D]. 长沙: 湖南大学, 2017. ZHU Xiaohui. Research on hysteretic performance of concrete frame joints[D]. Changsha: Hunan University, 2017.

[15] Lowes L N, Altoontash A. Modeling reinforced concrete beam-column joints subjected to cyclic loading[J]. Journal of Structural Engineering, 2003, 129(12): 1686− 1697.

[16] Altoonrash A. Simulation and damage models for performance assessement of reinforced concrete beam- column joints[D]. California: Stanford University, 2004.

[17] Lowes L N. Finite element modeling of reinforced concrete beam-column bridge connections[D]. California: University of California, 1999.

[18] Mitra N. An analytical study of reinforced concrete beam-column joint behavior under seismic loading[D]. Washington: University of Washington, 2007.

[19] 张鹏. 再生混凝土结构抗震性能非线性分析[D]. 青岛: 山东科技大学, 2005. ZHANG Peng. Nonlinear analysis of seismic behavior of recycled concrete structures[D]. Qingdao: Shandong University of Science and Technology, 2005.

[20] 唐昌辉. 无粘结预应力混凝土梁和型钢混凝土柱的试验与研究[D]. 长沙: 湖南大学, 2003. TANG Changhui. Experiments and researches on unbond presrtressed concrete columns[D]. Changsha: Hunan University, 2003.

Research on hysteretic performance of concrete frame with beam-column joint bonding–slip model

TANG Changhui, HUANG Chaomiao

(School of Civil Engineering, Hunan University, Changsha 410082, China)

Utilizing the beam-column joints element and bond-slip model of OpenSEES, the author analyzed the hysteresis performance obtained from horizontal low cycle reciprocating load test of reinforced concrete frame and steel reinforced concrete frame that have been completed by domestic researchers, including the hysteresis curve, displacement ductility, hysteresis area and energy dissipation capacity, and compared simulation results with test results. Based on the simulation results, the author established the calculation model of concrete frame and steel reinforced concrete combine frame with macroscopic mechanical model, which provides a convenient way for the design and calculation of concrete frame and steel reinforced concrete combine frame.

steel reinforced concrete frame; macroscopic mechanical model of joints; OpenSEES; hysteresis curve; bond-slip

10.19713/j.cnki.43−1423/u.2019.03.022

TU375.4

1672 − 7029(2019)03 − 0729 − 08

2018−03−23

国家自然科学基金资助项目(51338004)

唐昌辉(1963−)，男，湖南新宁人，副教授，博士，从事预应力和组合结构研究；E−mail：2863472302@qq.com

(编辑蒋学东)