曲线地段钢弹簧浮置板轨道振动特性试验研究

王刘翀，刘冬娅，易强，赵才友，王平



曲线地段钢弹簧浮置板轨道振动特性试验研究

王刘翀1, 2，刘冬娅1, 2，易强1, 2，赵才友1, 2，王平1, 2

(1. 高速铁路线路工程教育部重点实验室，四川 成都 610031； 2. 西南交通大学 土木工程学院，四川 成都 610031)

为探究曲线地段钢弹簧浮置板轨道结构振动特性，分别在钢弹簧浮置板轨道和普通道床的曲线地段进行现场测试，采用短时傅里叶变换对测试数据进行时-频处理，分析轨道结构振动时频特性。相比普通道床，在钢弹簧浮置板轨道中，钢轨和道床板振动幅值增大，振动频率向高频移动；道床板时频分布的峰值频率与车辆类型和激励原因有关；浮置板轨道中，隧道壁垂向加速度级减小23 dB，横向加速度级则增大6 dB，主要表现在8~50 Hz；隧道壁振动受到轨道板横向振动激励和浮置板轨道振动传递特性两者的影响，通过这个角度解释了曲线地段地段浮置板轨道中隧道壁横向振动放大的原因。

钢弹簧浮置板；曲线地段；振动；时-频分析

近年来，我国城市轨道交通快速发展，给居民出行带来了便利，但同时也给周围环境带来振动噪声等不良影响[1−3]。尤其在曲线地段，列车经过时通常会引起地面较大的水平和垂向振动[4]。随着人们对轨道交通环境振动问题的重视，目前已有多种控制技术手段，如减振扣件[5]、橡胶隔振垫[6]和钢弹簧浮置板等[7−8]。其中钢弹簧浮置板轨道减振效果良好，在地铁线路中被广泛应用[9]。目前国内外对钢弹簧浮置板已有大量研究，但由于曲线地段轮轨相互作用关系复杂，给钢弹簧浮置板在曲线地段的动力特性研究带来一定困难。苏云[10]建立浮置板轨道横向运动的数值模型，分析浮置板轨道横向振动的谐响应特性，得到弹性支承横向刚度对钢轨横向位移的影响规律。李响等[11]对地铁小半径曲线段钢弹簧浮置板轨道上的钢轨波磨进行研究，推测曲线段钢弹簧浮置板钢轨磨耗主要原因是浮置板受到列车轮缘挤压，浮置板向下移动，导致曲线段钢弹簧浮置板上的钢轨波磨位于轨面中央。从以上研究可以看出，钢弹簧浮置板在曲线地段存在复杂的振动传递关系，且容易出现钢轨横向位移、倾斜、波磨等问题。针对以上问题，本文基于短时傅里叶变换方法，对列车荷载作用下的曲线地段钢弹簧浮置板振动响应信号做时频域联合分析，并解释钢弹簧浮置板在曲线地段的振动特性。对比2组断面的钢轨、道床板、隧道壁横向、隧道壁垂向的振动加速度级，分析钢弹簧浮置板对各结构的影响并探究振动在轨道结构中的传递规律。

1 试验概况

1.1 断面概况

为研究曲线地段钢弹簧浮置板的振动特性，在线路条件基本一致的浮置板道床和普通道床各选一个曲线地段断面，断面选择在圆曲线段曲中点位置，避免缓和曲线轮轨力变化的影响。选取断面曲线半径为600 m，测点断面平面位置如图1所示，具体参数如表1所示。

表1 测点断面线路概况

1.2 车辆参数

采用地铁Ｂ型车，6辆编组，设计轴重14 t，接触轨供电，最高行车速度80 km/h。车辆外型尺寸长19 000 mm，宽2 800 mm，高3 800 mm。列车总长(列车两端连接面间长度)117.2 m。

现场测试时为空车荷载，经过断面时的速度大约在60~65 km/h。

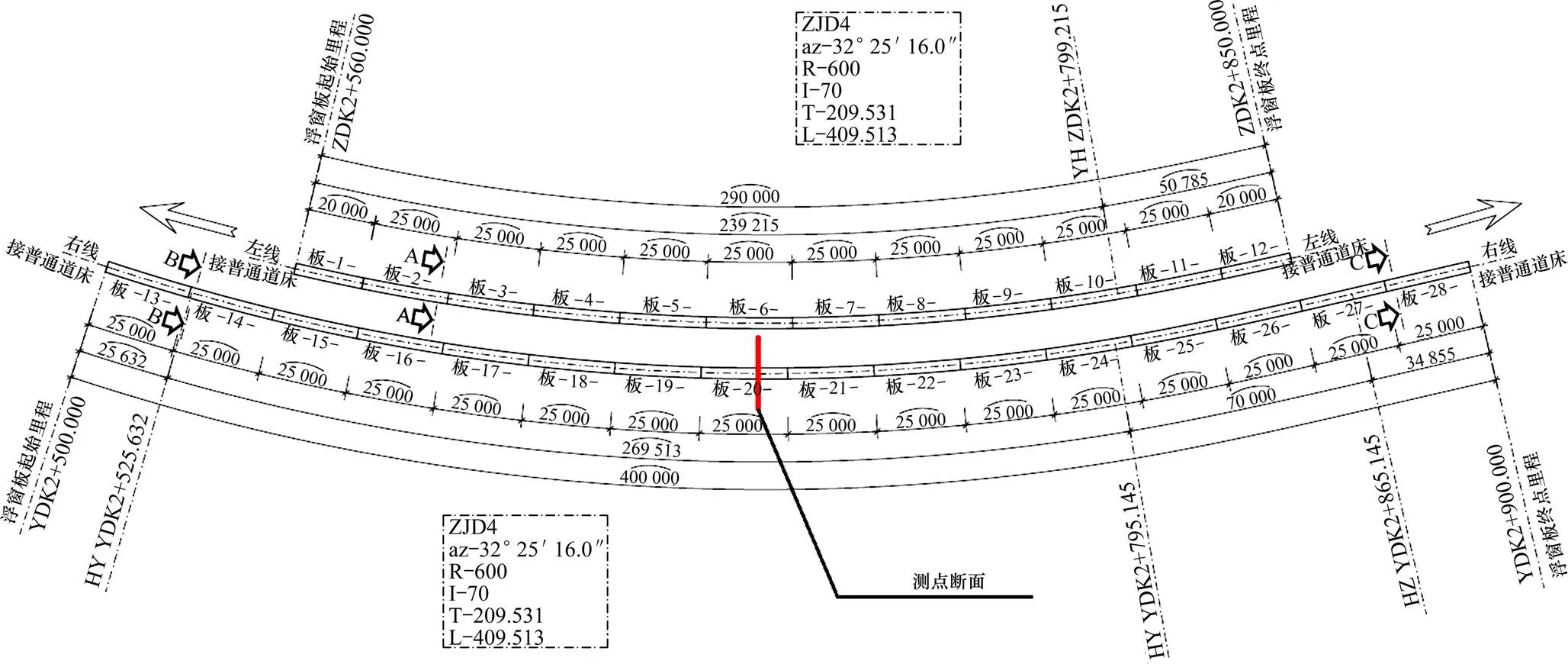
图1 钢弹簧浮置板测点平面示意图

1.3 测点布置

分别在钢轨(曲线内轨)垂向、道床板垂向、隧道壁垂向、隧道壁横向布置加速度传感器，实测列车通过时的振动加速度值(由于钢轨和道床板只布置了垂向测点，后文在描述时不再赘述其振动加速度方向)。图2为测点布置的横断面示意图，图中A测点布置在内侧钢轨轨底扣件之间跨中处，B测点布置在道床板处，C和D测点布置在距离轨顶高度1.25 m隧道壁处。A测点和B测点布置竖向加速度传感器，C测点布置了垂向加速度拾振器，D测点布置了横向(垂直于线路方向)的加速度拾振器。A，B，C和D 4个测点布置在同一隧道横断面。

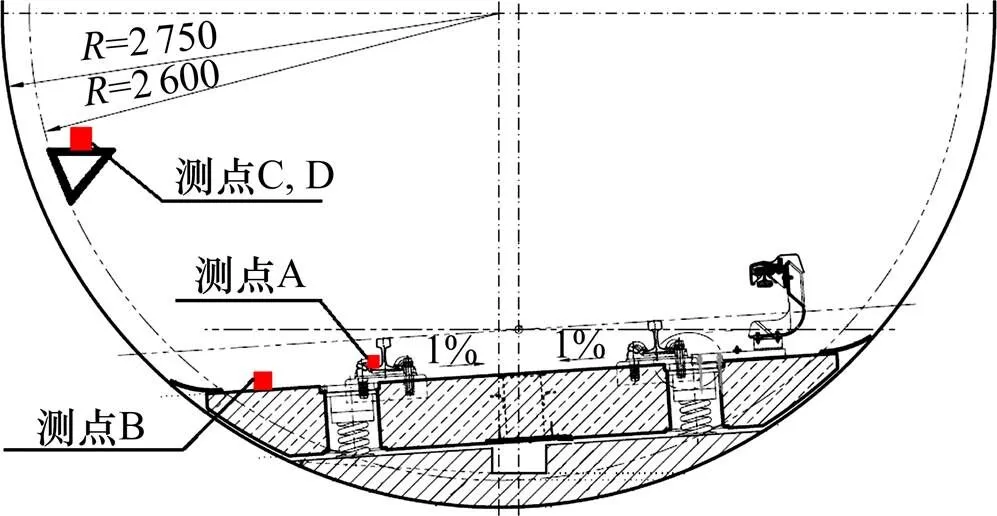
图2 测点布置横断面示意图

2 振动加速度时−频分析

对采集的时域振动信号进行筛选，选取波形完整、无明显畸变、信噪比高、无工频干扰或不严重的实测数据。采用短时傅里叶变换，得到2组断面各测点振动加速度的典型时−频分布。

2.1 钢轨

图3为普通道床段的钢轨振动加速度时频分布。图中A部分为钢轨振动加速度时程曲线，B部分为加速度频谱，C部分为振动加速度时频分布图，其中横坐标时间与时程曲线对应，纵坐标频率与频域谱对应，颜色代表的物理量为加速度在时间和频率的分布密度，单位为m/s2。

图4为钢弹簧浮置板道床钢轨振动加速度时频分布图。通过分析2组断面钢轨振动加速度在时频域中的分布规律，可以得到以下结论：

普通道床与钢弹簧浮置板2组断面中，6节编组列车的各转向架对应的钢轨振动加速度最大值分别为150 m/s2和300 m/s2，说明浮置板对钢轨振动有一定放大作用；其振动峰值出现频率分别在800 Hz和1 000 Hz，可知在钢弹簧浮置板段，钢轨振动频率向高频移动。

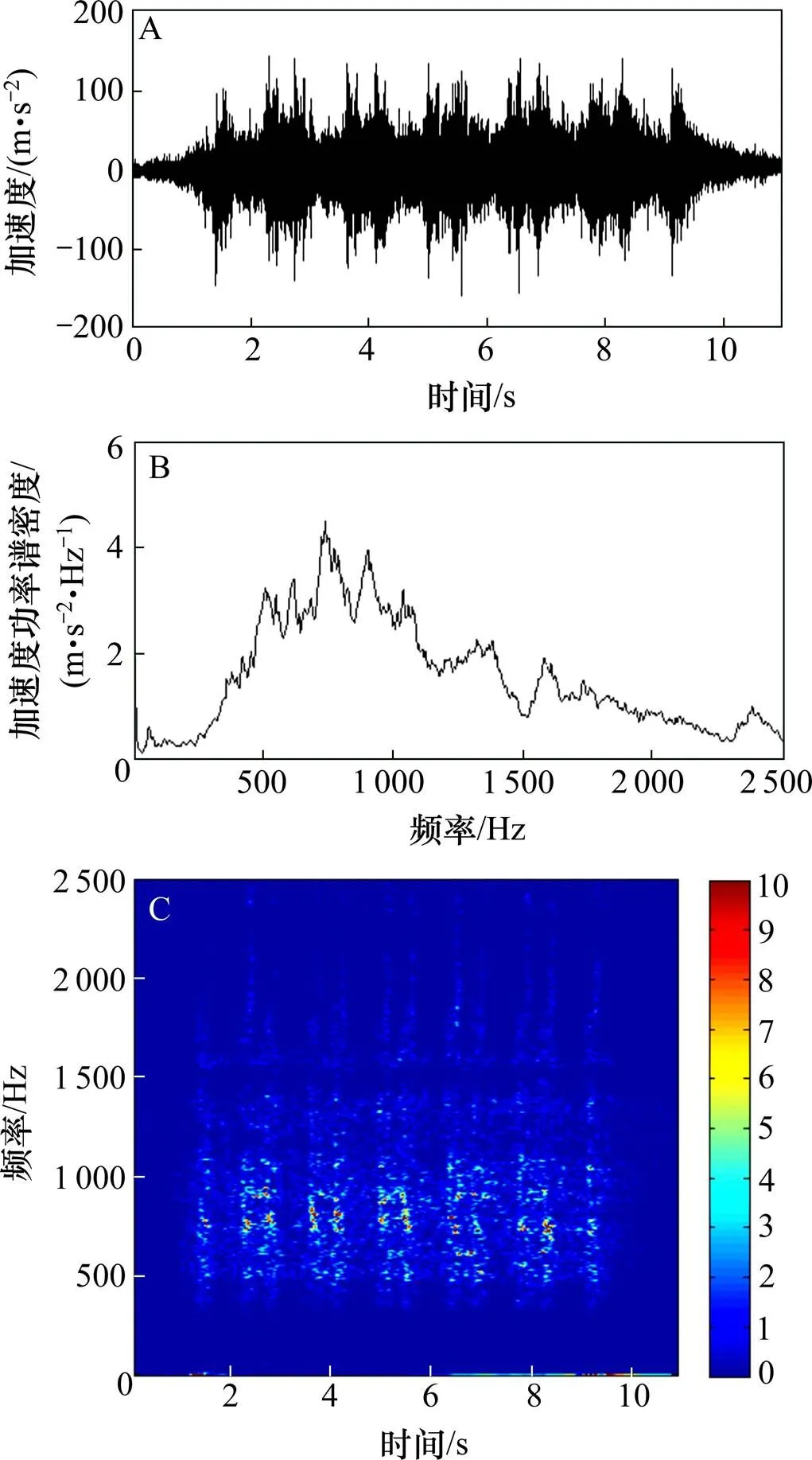
图3 普通道床钢轨振动加速度时频分布图

钢弹簧浮置板的钢轨加速度时频分布图中，1 000 Hz左右的亮斑在时程内连续，不能明显分辨出转向架对应的加速度峰值。推测是由于扣件离散支承引起的钢轨“pinned-pinned”共振模态[12]，钢轨产生驻波，相邻扣件中间位置(本文测点位置)的钢轨垂向导纳达到峰值，各个时域波峰相互叠加导致。

图4 钢弹簧浮置板轨道钢轨振动加速度时频分布图

2.2 道床板

图5和图6分别为普通道床地段与钢弹簧浮置板地段的道床板振动加速度时频分布。经分析得到以下结论：

加速度时程曲线中，普通道床地段可以较清楚看出列车各转向架对应的道床板振动加速度峰值，加速度最大值为1.5 m/s2；钢弹簧浮置板地段，较难辨认转向架对应的振动加速度波峰，振动加速度最大值为10 m/s2。钢弹簧浮置板会大大加剧道床板的振动。

加速度频谱中，普通道床地段道床板的最大峰值频率为75 Hz，优势频率集中在60~100 Hz；钢弹簧浮置板段的振动加速度优势频率在40~120 Hz均有分布，高频成分较多。

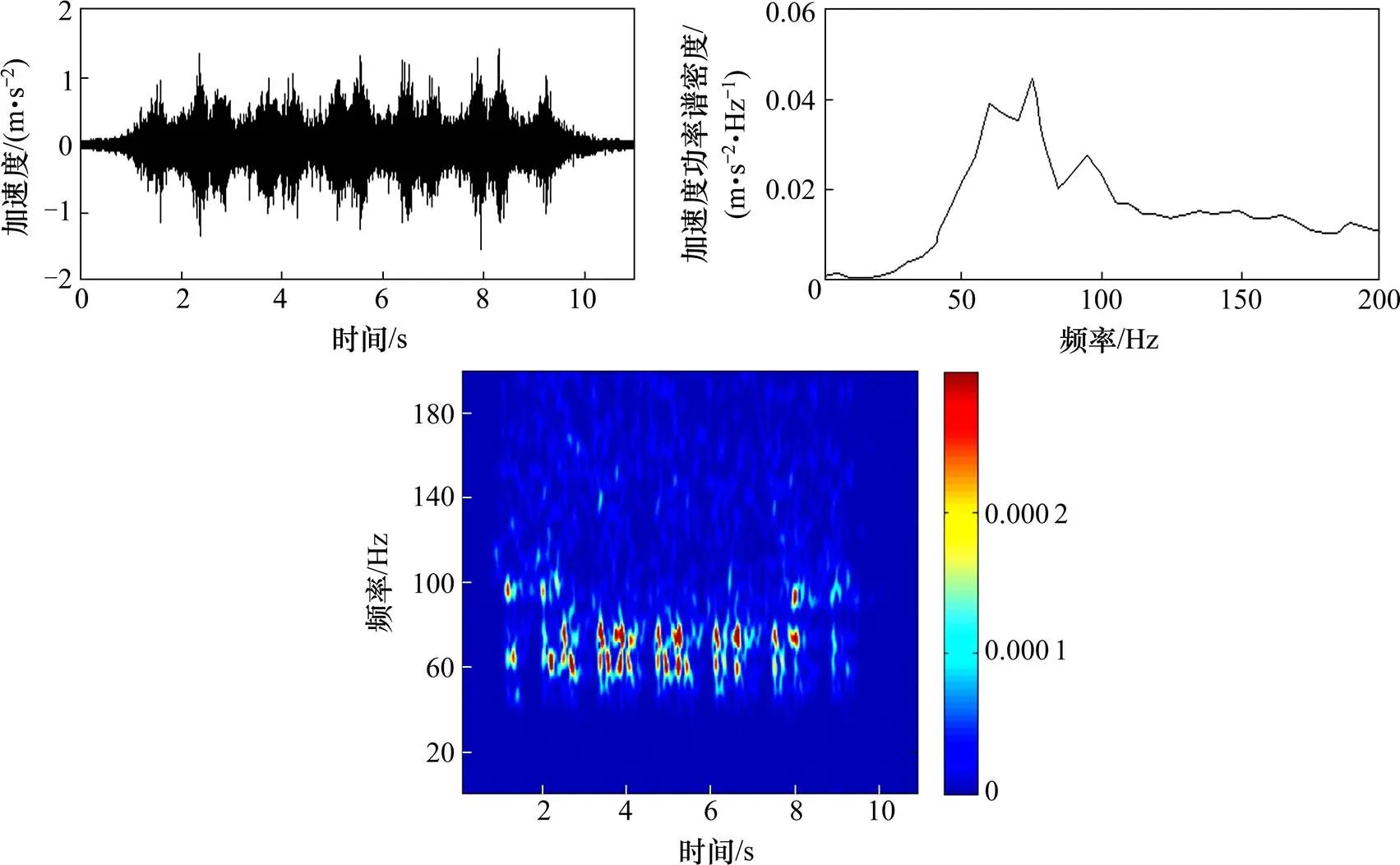
图5 普通道床道床板振动加速度时频分布

图6 钢弹簧浮置板轨道道床板振动加速度时频分布图

分析普通道床段时频分布图，用灰点在时频分布图中标记与转向架对应的亮斑，如图7所示。

图7(a)为转向架轮对经过测点位置的3种情况。从图7(b)中可以看到中间车厢转向架在经过测点断面时均激励60 Hz和75 Hz的振动，第1节车厢的转向架激励60 Hz和100 Hz的振动，第6节车厢的转向架可以激励75 Hz和100 Hz的振动。这与车辆自身轴重、车辆前后约束状态有关。

采用同样的方法，根据转向架对应位置对时频分布图作一定整理，如图8所示。

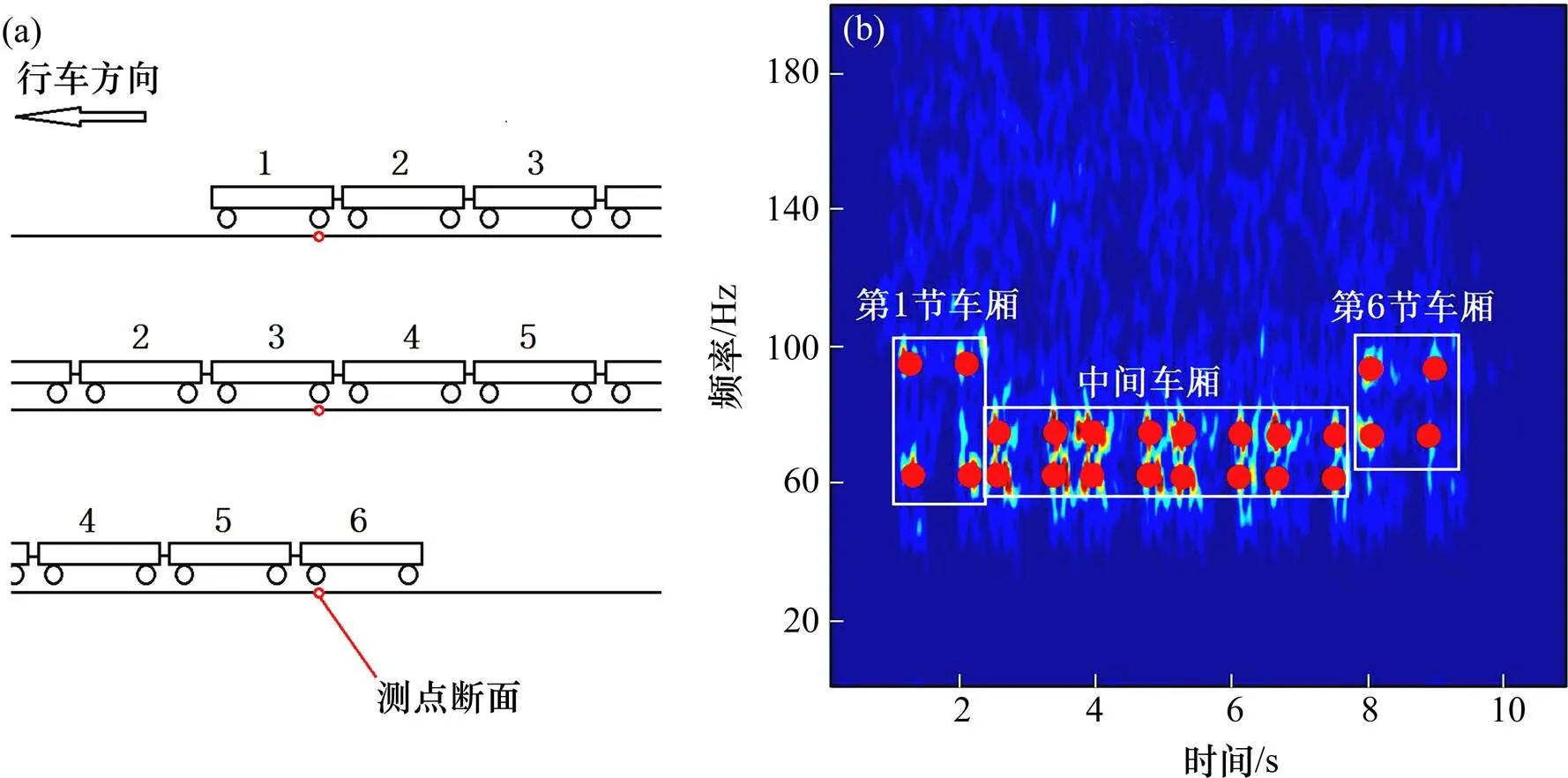
(a) 转向架相对测点位置示意图；(b) 道床板振动加速度时频分布图

图8 列车经过钢弹簧浮置板轨道测点情况示意

由图8可知，转向架经过测点时主要会激励90 Hz和120 Hz的振动，相较普通道床中60 Hz和75 Hz，频率有所升高；在40 Hz左右出现的一组亮斑，发生在转向架经过测点位置之前，通过车速与相隔时间计算，振动发生间距与浮置板一半长度接近。推测是由于转向架经过浮置板间隙时引起的浮置板整体振动。

2.3 隧道壁

2.3.1 隧道壁垂向

图9和图10分别为普通道床与钢弹簧浮置板轨道的隧道壁垂向振动加速度时频分布。经分析得到以下结论：

普通道床中，隧道壁垂向加速度时程曲线最大值为0.15 m/s2，仍可以分辨对应转向架的尖锐峰值；加速度频域分布的优势频率为60 Hz和75 Hz。

钢弹簧浮置板轨道中，隧道壁垂向加速度时程曲线最大值为0.01 m/s2，且已经无法辨认转向架对应的峰值。说明钢弹簧浮置板能够有效减小隧道壁的垂向振动幅值，且对冲击荷载有较好的抑制；加速度频谱中可以看到10 Hz的峰值，这是由于浮置板减振系统对器固有频率附近的振动减振效果不佳导致的。

时频分布图中，普通道床段隧道壁垂向振动峰值与道床板的振动峰值分布规律基本一致，振动从道床板传播到隧道壁垂向时，幅值减小，频率不变。钢弹簧浮置板段隧道壁垂向振动在40，90和120 Hz的亮斑与道床板振动峰值对应。75 Hz左右的亮斑与浮置板垂向振动传递特性有关。

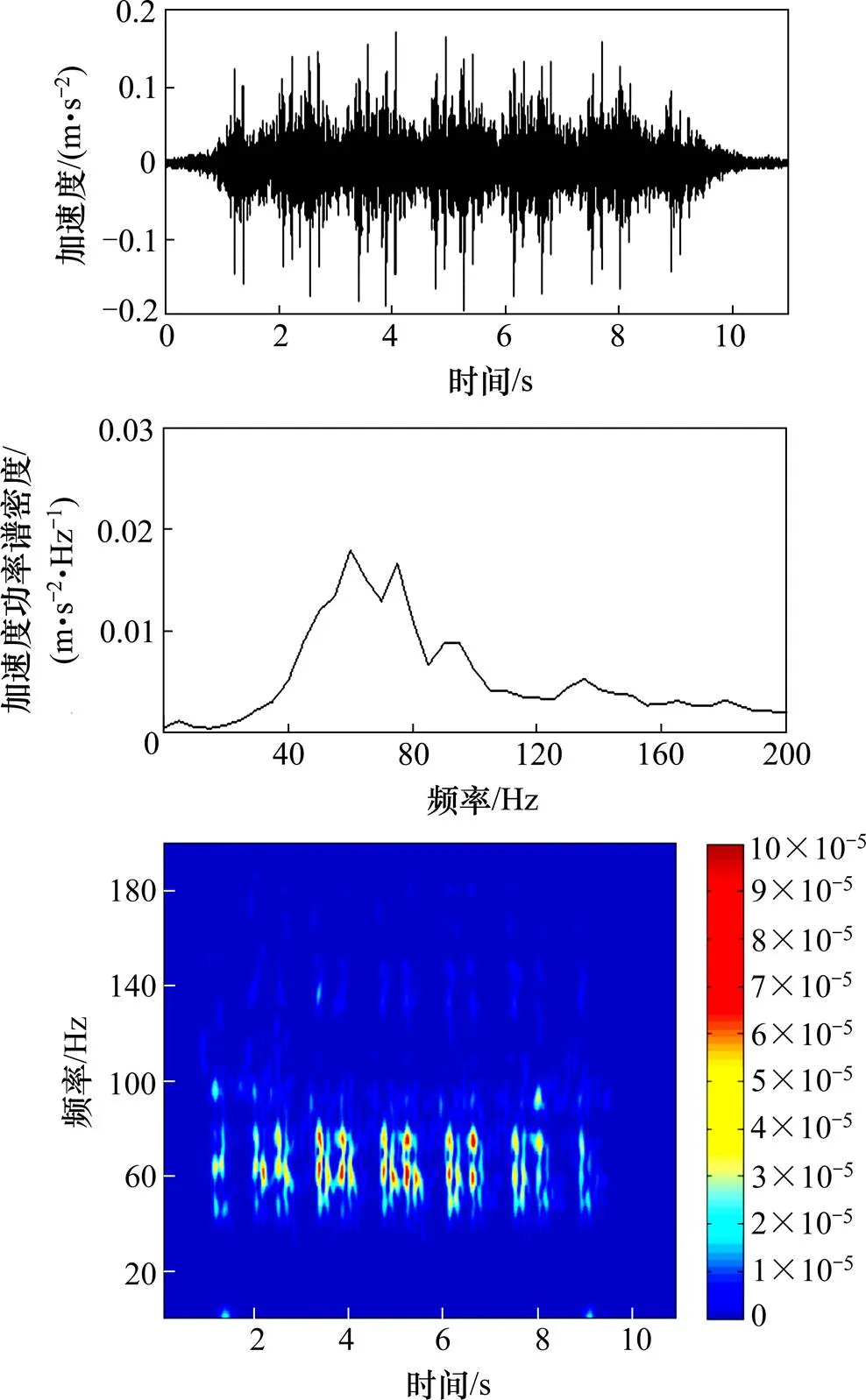
图9 普通道床道隧道壁垂向振动加速度时频分布

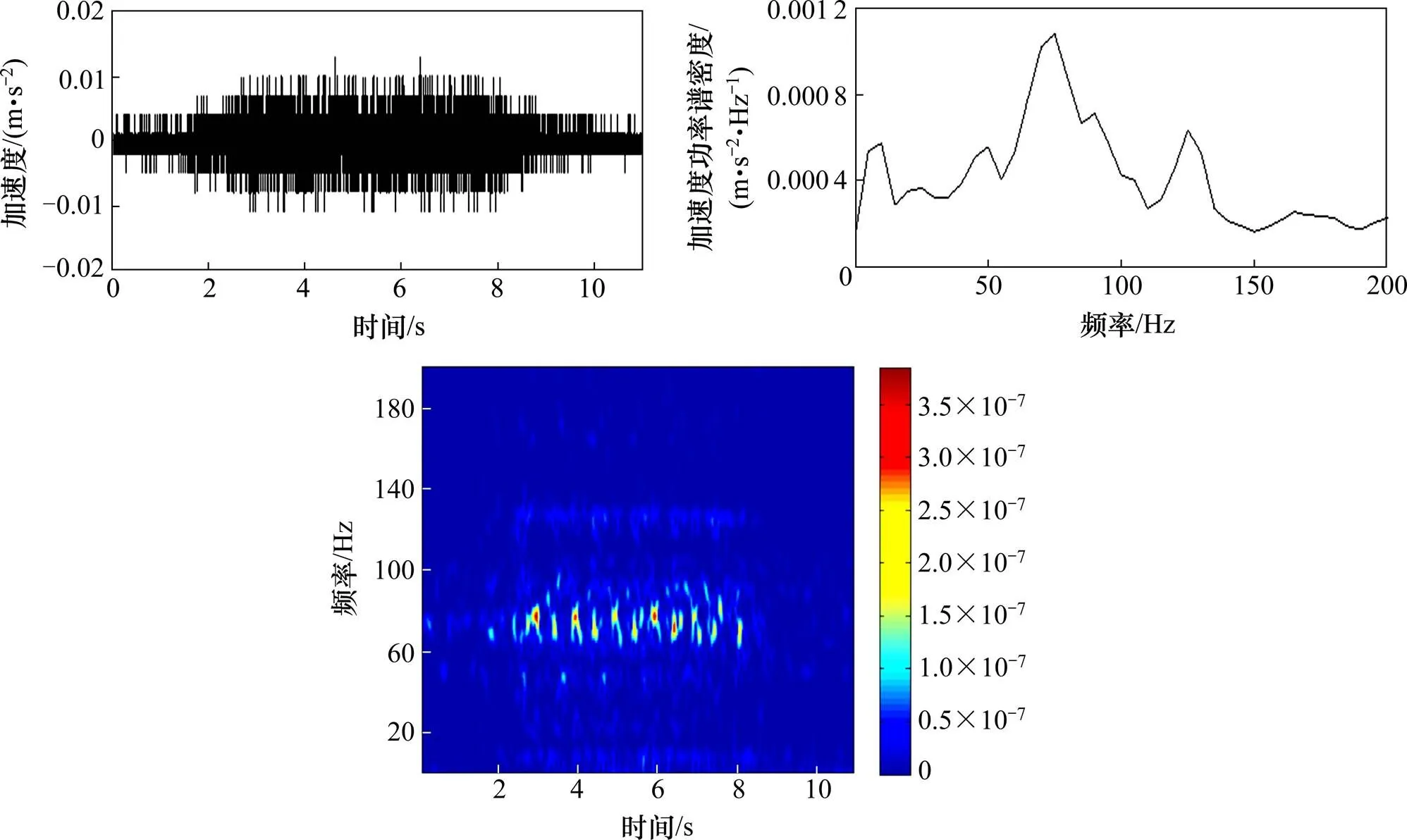
图10 钢弹簧浮置板隧道壁垂向振动加速度时频分布

2.3.2 隧道壁横向

图11和图12分别为普通道床与钢弹簧浮置板轨道的隧道壁垂向振动加速度时频分布。经分析得到以下结论：

普通道床和浮置板轨道中，隧道壁横向加速度时程曲线最大值分别为0.3 m/s2和0.2 m/s2。与垂向加速度一样，转向架对应的毛刺峰值在浮置板轨道中被消去。

图11 普通道床道隧道壁横向振动加速度时频分布图

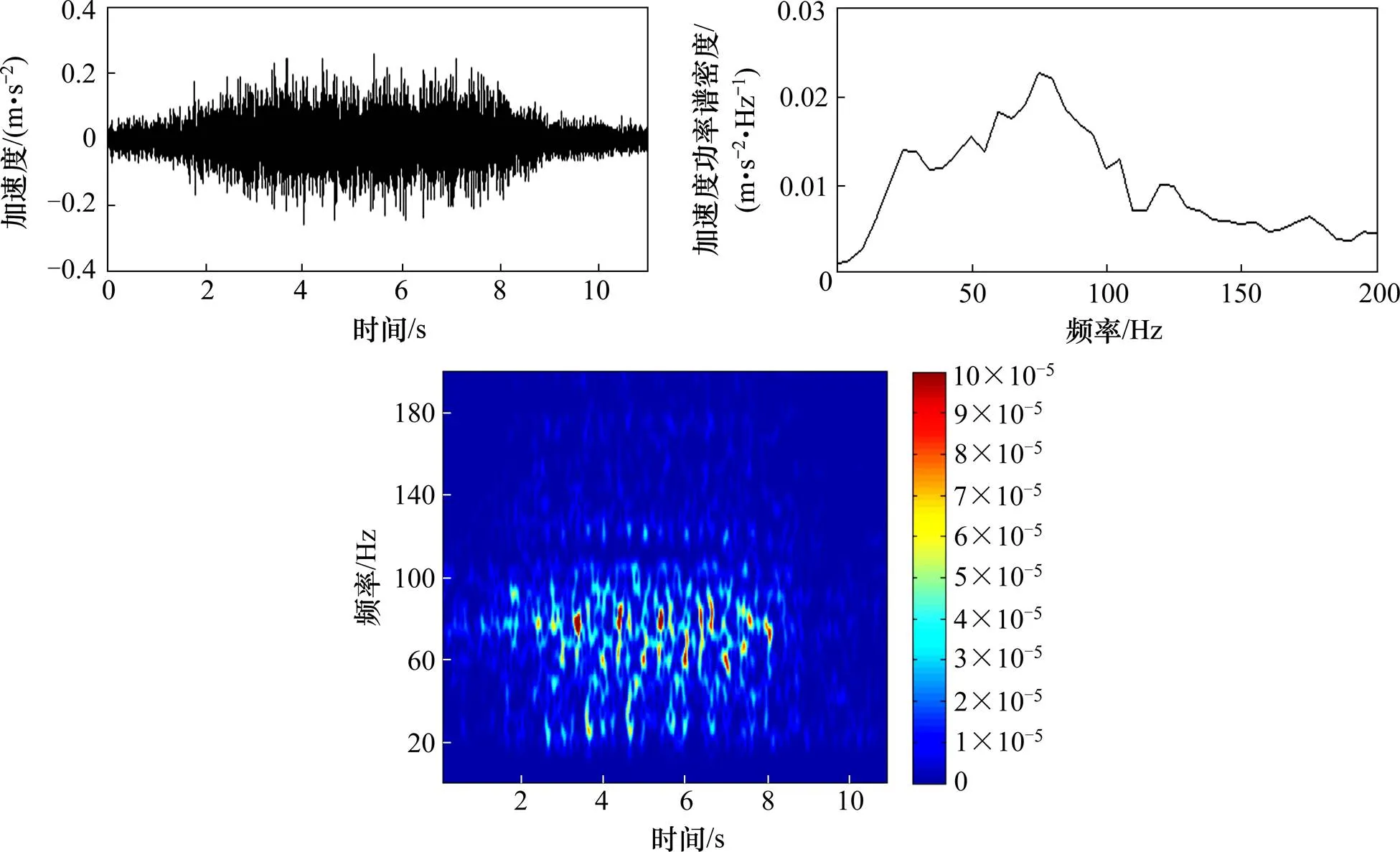
图12 钢弹簧浮置板轨道隧道壁横向振动加速度时频分布图

普通道床地段隧道壁横向振动的优势峰值频率为60 Hz和75 Hz，与隧道壁垂向振动一致；钢弹簧浮置板地段，隧道壁横向振动在20~120 Hz均有较大幅值，低频成分增加。

时频分布图中，普通道床中隧道壁横向振动规律与隧道壁垂向基本一致。浮置板轨道中隧道壁横向振动时频分布在60 Hz和75 Hz处可以分辨出转向架对应的振动亮斑，与普通道床段横向振动亮斑相似，又有自身振动特性导致的亮斑混杂。其中20 Hz的振动峰值，与钢弹簧浮置板的横向振动模态有关。

3 振动加速度级分析

本文只讨论轨道和隧道壁的振动，不涉及振动环评，因此采用不计权的振动加速度级进行分析。图13(a)~13(c)整理了2组断面钢轨、道床板、隧道壁振动加速度级1/3倍频程图。

图13(a)中浮置板轨道中的钢轨的加速度级在0~80 Hz低频范围略小。插入损失最大值发生在10 Hz达13 dB。插入损失表示普通道床与钢弹簧浮置板轨道中各个轨道结构振动加速度级差值。

图13(b)中，浮置板段道床板加速度级在全频段都有明显的放大。其中在12.5 Hz加速度动放大最剧烈，插入损失为−43 dB。

图13(c)中，钢弹簧浮置板能有效减小隧道壁垂向振动，主要体现在20 Hz以上的频段。插入损失最大值发生在63 Hz达27 dB，全频段加速度级插入损失为23 dB。

通过以上垂向振动在各结构振动加速度级分布可知，钢轨、道床板和隧道壁振动加速度级依次递减，钢弹簧浮置板在振动传递过程中起到动力吸振器的作用，振动能量在道床板中聚集。

由图13(d)分析可知，列车在曲线段钢弹簧浮置板轨道运行时，隧道壁横向振动加速度级在8~50 Hz存在一定放大，在16 Hz左右存在−28 dB的插入损失谷值。80 Hz以上分频振动加速度级大小与普通道床相当。全频段加速度级插入损失为−6 dB。

综合以上时−频分布和1/3倍频程振动加速度级，分析隧道壁横向加速度峰值小却振动加速度级增大原因：钢弹簧浮置板对冲击振动有一定缓冲作用，因此加速度时程曲线的毛刺峰值被消除。但钢弹簧浮置板地段钢轨和道床板振动加剧，线路几何形位保持能力弱，轮轨相互作用增强，因此导致了隧道壁横向振动加速度级增大。

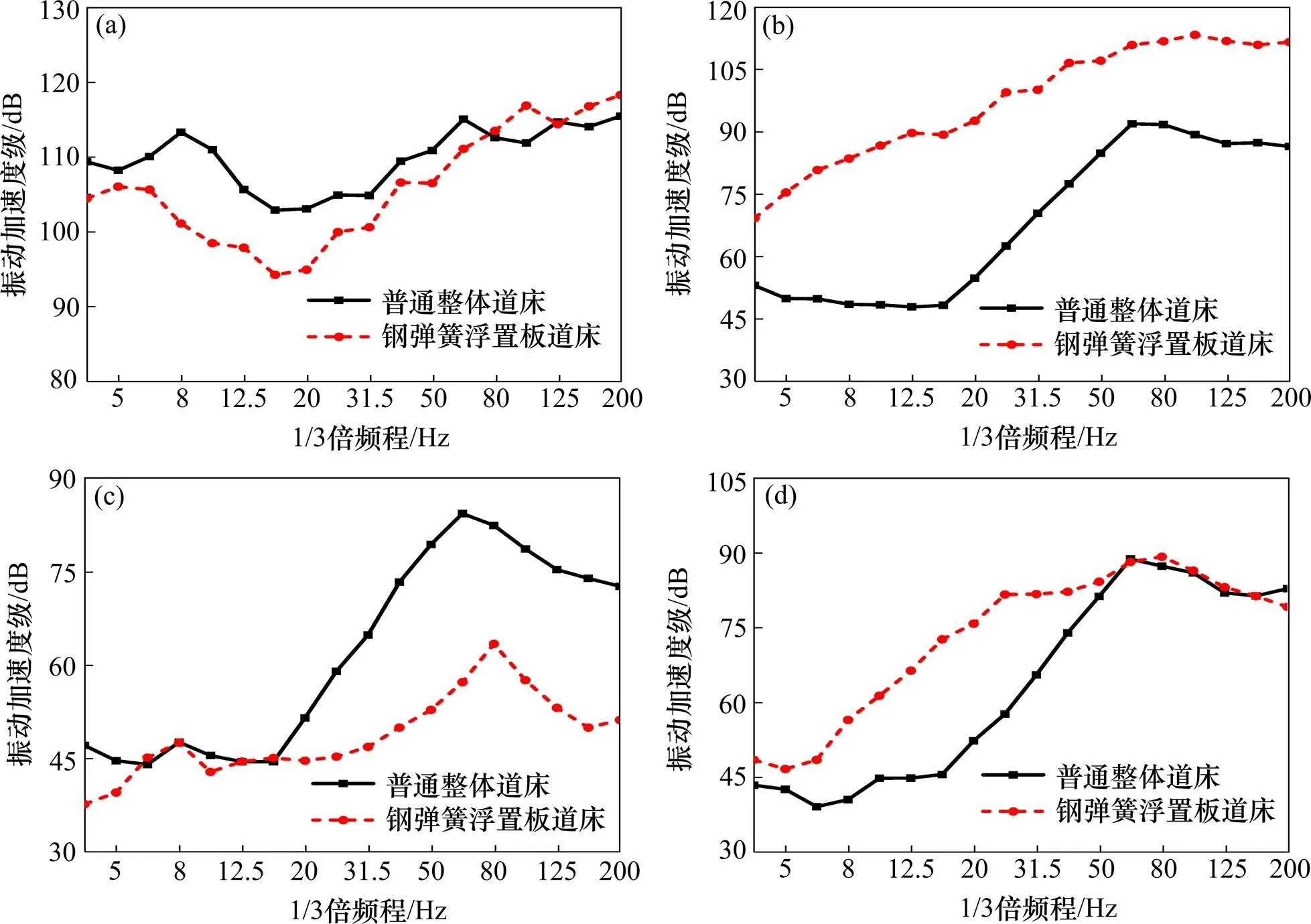
(a) 钢轨；(b) 道床板；(c) 隧道壁垂向；(d) 隧道壁横向

4 结论

1) 在钢弹簧浮置板地段，钢轨振动幅值增大，频率向高频移动，在1 000 Hz出现振动加速最大值。在80 Hz以下低频范围，道床板振动幅值显著增大，优势频率分布广，高频成分增加。

2) 转向架引起道床板的振动频率与转向架对应的车辆类型和激励原因有关。在普通道床地段，车头和车尾的转向架经过测点位置时会激励100 Hz的振动峰值，中间车厢主要激励60 Hz和75 Hz的振动峰值；在钢弹簧浮置板地段，转向架经过测点断面主要激励90 Hz和120 Hz的振动峰值。转向架经过浮置板间隙时会引起道床板40 Hz的整体振动。

3) 在普通道床地段，隧道壁垂向振动峰值与道床板的振动峰值分布规律基本一致；在钢弹簧浮置板地段，隧道壁垂向振动峰值分布与浮置板振动传递特性和固有频率两者有关。浮置板的10 Hz的垂向振动模态和20 Hz的横向振动模态，导致在隧道壁垂向和横向振动频谱中出现相应峰值。

4) 钢弹簧浮置板可以减少隧道壁垂向加速度级23 dB，横向振动加速度级则增大6 dB，主要表现在8~50 Hz。推测在曲线地段浮置板轨道中轮轨相互作用增强，浮置板对横向振动的减振作用不大，导致隧道壁横向振动加速度级增大。

[1] Bata M. Effects on buildings of vibration caused by traffic[J]. Journal of Building Science, 1971, 6(4): 221− 246.

[2] 夏禾, 曹艳梅. 轨道交通引起的环境振动问题[J]. 铁道科学与工程学报, 2004, 1(1): 44−51. XIA He, CAO Yanmei. Problem of railway traffic induced vibrations of environments[J]. Journal of Railway Science and Engineering, 2004, 1(1): 44−51.

[3] Rafał B, Bogusław N. Identification of the Vibration Environment of Railway Infrastructure[J]. Procedia Engineering, 2017(187): 556−561.

[4] 张燕. 曲线地段地铁诱发的大地振动规律探讨[J]. 铁道建筑, 2015(8): 76−79. ZHANG Yan. Exploring on regularity of ground vibration induced by metro train running at curved section[J]. Railway Engineering, 2015(8): 76−79.

[5] 王文斌, 刘维宁, 贾颖绚, 等. 更换减振扣件前后地铁运营引起地面振动的研究[J]. 中国铁道科学, 2010, 31(1): 87−92. WANG Wenbin, LIU Weining, JIA Yingxuan, et al. Research on the vibration of the ground caused by metro train operation before and after changing the damping fasteners[J]. China Railway Science, 2010, 31(1): 87−92.

[6] 赵才友, 王平. 桥上无砟轨道橡胶减振垫减振性能试验研究[J]. 中国铁道科学, 2013, 34(4): 8−13. ZHAO Caiyou, WANG Ping. Experimental study on the vibration damping performance of rubber absorbers for ballastless tracks on viaduct[J]. China Railway Science, 2013, 34(4): 8−13.

[7] LEI Xiaoyan, JIANG Chongda. Analysis of vibration reduction effect of steel spring floating slab track with finite elements[J]. Journal of Vibration and Control, 2016, 22(6): 1462−1471.

[8] 耿传智, 楼梦麟. 浮置板轨道结构系统振动模态分析[J]. 同济大学学报(自然科学版), 2006, 34(9): 1201− 1205. GENG Chuanzhi, LOU Menglin. Vibration model analysis of floating slab track system[J]. Journal of Tongji University (Natural Science), 2006, 34(9): 1201−1205.

[9] 吴宗臻, 刘维宁, 马龙祥, 等. 地铁浮置式轨道引起地表振动响应解析预测模型研究[J]. 振动与冲击, 2014, 33(17): 132−137. WU Zongzhen, LIU Weining, MA Longxiang, et al. Analytical prediction model of ground vibration response induced by metro floating-type track[J]. Journal of Vibration and Shock, 2014, 33(17): 132−137.

[10] 苏云. 浮置板轨道横向动力学特性研究[D]. 上海: 上海交通大学, 2012. SU Yun. Research on lateral dynamic characteristics of floating slab track[D]. Shanghai: Shanghai Jiaotong University, 2012.

[11] 李响, 任尊松, 徐宁. 地铁小半径曲线段钢弹簧浮置板轨道的钢轨波磨研究[J]. 铁道学报, 2017, 39(8): 70−76. LI Xiang, REN Zunsong, XU Ning. Study on rail corrugation of steel spring floating slab track on subway with small radius curve track.[J]. Journal of the China Railway Society, 2017, 39(8): 70−76.

[12] David T, Chris J. Reply to comments on Chapter 12 of “Railway Noise and Vibration: Mechanisms, Modelling and Means of Control”, by D. Thompson (with contributions from C. Jones and P.-E. Gautier), Elsevier, 2009[J]. Applied Acoustics, 2011, 72(10): 787−788.

Field test on vibration characteristic of steel-spring floating slab track in curve section

WANG Liuchong1, 2, LIU Dongya1, 2, YI Qiang1, 2, ZHAO Caiyou1, 2, WANG Ping1, 2

(1. Key Laboratory of High-speed Railway Engineering, Ministry of Education, Chengdu 610031, China; 2. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China)

To study the vibration characteristics of the steel-spring floating slab track on metro curve section, the field test on dynamic response of steel-spring floating slab track and normal track was conducted in the curve section. Short- time Fourier transform (STFT) was applied to analyze time-frequency vibration characteristics of the rail (vertical), slab (vertical), tunnel wall (vertical and lateral). Comparing to vibration characteristics of normal track, the results show as follows: in the steel-spring floating slab track, the vibration amplitude of the rail is increased and more high frequency component is produced. The vibration amplitude of the slab is increased and the dominant frequency is widely distributed at 40~120 Hz. The peak frequency of the time-frequency distribution of the slab vibration is related to vehicle type and the cause of the incentive. The degree of Z direction vibration of the tunnel wall (vertical) is reduced by 19 dB, and the vibration acceleration level of tunnel wall (lateral) is enlarged by 6 dB, which is mainly increased at 8~50 Hz. The tunnel wall vibration is affected by the vibration of the slab and the vibration characteristics of the floating slab track.

steel-spring floating slab; curve section; vibration; time-frequency analysis

10.19713/j.cnki.43−1423/u.2019.03.008

U231；TB53

A

1672 − 7029(2019)03 − 0610 − 10

2018−04−26

国家重点研发计划资助项目(2016YFE0205200)；国家杰出青年科学基金资助项目(51425804)；青年科学基金资助项目(51508479)；四川省重点研发项目(2017GZ0373)

王平(1969−)，男，湖北宜昌人，教授，博士，从事无砟轨道结构及轨道动力学研究；E−mail：wping@home.swjtu.edu.cn

(编辑 涂鹏)