大洋中涌浪对风浪能量的影响❋
2019-04-16赵栋梁
贾 楠, 赵栋梁, 2❋❋
(1.中国海洋大学海洋与大气学院, 山东 青岛 266100; 2.中国海洋大学物理海洋实验室, 山东 青岛 266100)
海洋中风浪、涌浪往往相依相伴,共同出现。风浪直接从风摄取能量,涌浪不直接从风摄取能量,甚至会将能量传递给风[1]。涌浪与风浪在波长、波速、频率等特征物理参量上显著不同,二者的成长、衰亡过程也不一样[2]。因此,研究二者之间的相互作用,对海浪预报、防灾减灾等有重要的意义。
由于风浪、涌浪二者之间相互作用颇为复杂,实验室和海上观测得出了不相同的结论,并且提出了多种解释方法。Longuet-Higgins 和Stewart[3]利用stokes二阶近似,指出长短波之间通过辐射应力做功传递能量,使短波在长波波峰处波长变短,波陡变大,在波谷处波长变长,波陡变小。Phillip等[4]加入风生漂流的作用,指出:在流的作用下,短波更易破碎,波峰处短波振幅被削减,从而改变风浪谱。Hatori等[5]研究表明,风浪会通过非线性过程向叠加的长波传递能量。Dobson等[6]通过现场观测发现有限风区的风浪成长不受反向涌浪影响。Mitsuyasu[7]实验室实验发现,风浪能量会因反向涌浪加强。Chu等[8]实验室观测到风浪会被同向涌浪衰减。Chen和Belcher[9]通过实验室实验,观测了风浪、涌浪单独存在及风涌浪同时存在时的谱形状,指出在特定水深、风速下,影响风能输入的主要因素是涌浪是否达到风速对应无限风区下的最大波高,而与风速、涌浪的波陡、波速、风涌浪频率等关系不大。他同时指出,实验室涌浪表面非常光滑,与外海条件不符。Yue等[10]指出,当长波为小波陡,且长短波频率之间相差较大时,Longuet-Higgins和Stewart[3]调制机制与波浪破碎共同作用,决定了长波(涌浪)对短波(风浪)的影响。截止目前,并没有统一理论解释不同作者的实验结果。由于海上实测因素很复杂,受观测手段、航海技术等限制,前人所做实验大多是在实验室进行,外海观测几乎没有。而实验室的观测能否直接应用于外海还未可知。近年进行了海湾的观测[11],以及外海高风速下[12]观测。前者数据量少且同实验室一样,海湾内波高处于1 m以下,不符合外海通常1~3 m条件,代表性不足。后者为高风速下数据,不符合中低风速情况。诸多的理论验证都存在很大的难度,需要进一步研究。
1 数据来源
本文的数据于2013-12-05—2014-01-04和2015-11-07—2016-01-07两个时间段走航观测得到。风速数据来源于船载自动气象站,该气象站装载于驾驶室上方船舶的最高处,高度为18 m。驾驶室位于船首,周围无障碍物遮挡,从而使船体对气象站的影响最小,保证风速的准确性。在进行数据分析之前根据风速廓线转换为10 m风速,波浪及流的数据来源于船载WaMoSⅡ 测波雷达,测波雷达在走航期间全天不间断工作,默认每隔两分钟输出一次数据,数据包括极坐标数据、谱数据以及前20 min的平均数据。2013年科考地点在南海,经纬度范围为102°E~115°E, 1°S~21°N。2015年科考地点在西太平洋,经纬度范围为135°E~161°E, 1°S~36°N。赤道无风带地区无风、浪小甚至无浪。随着纬度增大风速增大,浪高增大。南海夏季多发台风,海况多为3~5级,有效波高多处于1.5~3.5 m,最大有效波高为4.5 m。风速范围为0.5~17.5 m/s,风向多为东北方向。西太海况多为2~4级,有效波高多处于1~3 m,最大有效波高为4.5 m,涌浪较为显著,风速范围为0.5~18 m/s,风向多为东北风向,间或西南风。
2 测波雷达工作原理
测波雷达向海洋表面发射电磁波,电磁波回波信号作为雷达图像。一个采样周期包含32次连续采样,形成一个采样序列,对采样序列进行数据分析得到该次采样的波浪信息。具体处理过程如下:
(1) 雷达极坐标图像序列采样:测波雷达的硬件采集海面表的一系列雷达数字图像存储在硬盘里。
(2) 笛卡尔变换:测波雷达从整个极坐标图像中提取矩形次级区域,也叫分析区域进行坐标变换,从极坐标系转换到笛卡尔坐标系下。分析区域的大小、位置、时间长度可以在安装模式下进入控制/配置菜单进行设置。
(3) 离散傅里叶变换:使用离散傅里叶变换,将笛卡尔坐标系下的雷达图像序列转换为3D的波数频率谱。
(4) 3D图像谱的过滤机海表面流的确定:用频散关系做为带通滤波器,将波浪能量从背景噪音中分离出来,并且确定表面流。
(5) 确定清晰的2D图像谱:将3D谱在频域上进行积分,采用调制传递函数(MTF)得到清晰的2D波数谱。
(6) 计算波数方向谱。将2D波数谱转换成频率方向谱。
(7) 确定频谱和所有其他海浪参数:一系列统计波参数,例如波高、波长、波向等,从1D频率普中导出。
(8) 确定指定时间间隔的平均波浪参数:用谱平均发确定平均的2D谱。
3 测波雷达数据矫正
本文拟根据测波雷达所测风涌浪进行风涌浪相互作用的研究,因此在进行研究之前对测波雷达的数据做了分析矫正。
为了检验测波雷达的准确性,本文把测波雷达所得风浪数据与PM充分成长谱[13]作了对比分析。根据PM充分成长谱,可以计算出有效波高与风速的关系:
(1)
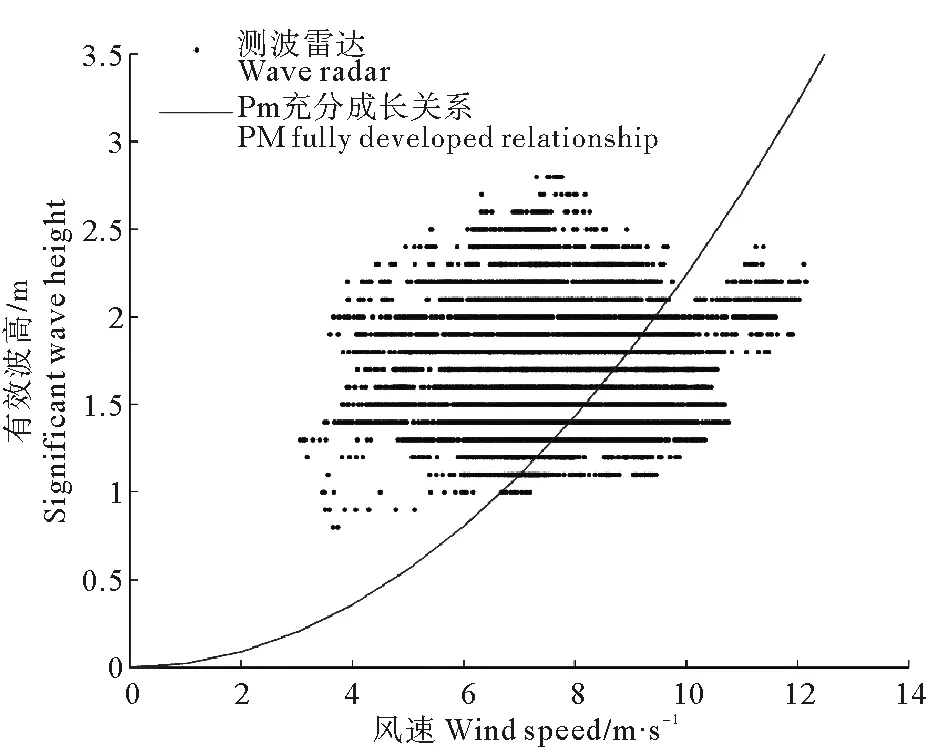
(点为测波雷达数据,曲线为由PM谱所给出的有效波高。The dots are the radar data, and the linerepresents is the significant wave height given by PM spectrum.)
图1 测波雷达所测风浪有效波高 与PM谱得到有效波高对比结果
Fig.1 The comparation of significant wave height between radar and the PM spectrum
图1为测波雷达观测所得风浪有效波高与PM充分成长谱得到有效波高对比结果。图1显示,风浪有效波高的的数值远远大于充分成长有效波高,最大可达1.5 m。且有超过一半的数据都处在PM充分成长关系上方。测波雷达所给出的风浪有效波高要普遍大于PM充分成长关系。这显然不符合实际结果。
对此,本文翻阅了测波雷达使用手册,发现测波雷达在将二维谱方向转换成一维频率谱时,只采用了周期作为分离标准,即分离出二维谱系统后,有效周期大于9 s的视为涌浪,小于9 s的视为风浪,风速、风向、波向等信息都被忽视,该分离标准显然不够精准。
国内外有很多文章都研究了风、涌浪的划分问题。分离判据可归纳为波型、波要素及谱分析三类。主要的波要素包括波高、波陡、波龄[14]。郭佩芳等[15]提出谱分析法,依据海浪谱的零阶矩,提出混合浪成分因子作为划分风、涌浪的方法。Li和Zhao[16]通过与实测资料对比得出,不同的判据所得分离结果有一定差异,2D法所得结果相较更为可靠。但是若把一维法与二维法相结合,将会得到更加准确的分离结果。
本文结合了二维法和一维法的判据,依照测波雷达数据特征,给出如下的风涌分离方案:
(1) 根据文献[17]把二维谱划分为不同的海浪系统。
(2) 计算各个海浪系统的有效波高,谱峰周期等波浪要素。
(3) 根据判据Tp=β×(2π/g)×U×cosθ,判断波浪类型为风浪或者涌浪。其中:Tp为该系统的谱峰周期;β为波龄判据;g为重力加速度;U为风速;θ是波浪平均方向与风向夹角。
(4) 把涌浪之外的波浪系统合并成一个风浪,计算风浪波浪要素。
(5) 判断剩余涌浪系统是否合并,合并判据是:分离角度小于30°,两谱峰距离小于任一分量谱宽度的2倍。计算合并之后各个涌浪分量波浪要素。
(6) 考虑到测波雷达的精确度,去掉风浪及涌浪分量中有效波高小于0.4 m的部分。

图2 使用不同波龄判据所得风浪有效波高与PM充分成长关系谱对比Fig.2 The comparation of significant wave height using different wave age criteria with the PM spectrum
图2对测波雷达谱数据进行分析,使用不同波龄作为判据得到风浪有效波高与PM谱对比,(a)、(b)、(c)波龄分别取为2、1.7、1.5。波龄取2时有大约三分之一的数据处于PM谱上方,有效波高相差最大可达1.5 m。波龄取1.7时有少部分数据处于PM谱上方,有效波高相差最大接近1 m。波龄取1.5时,只有个别数据处于PM谱上方,并且都在PM谱附近,因此,本文最终选取波龄判据为1.5。
4 大洋中风涌浪之间能量传递
Toba[18]根据无量纲法,从能量输入角度提出了3/2指数律,其中系数由实测数据确定。该定律反应了风浪成长关系,并为大量的实验观测所证实。赵栋梁[19]指出,Toba-3/2指数律不仅仅适用于风浪,同时对波龄远远大于1.4的海浪也适用。本文将以Toba-3/2指数律作为基础,对风涌浪之间的能量传递做初步探讨。
Toba-3/2指数律给出的无因次波高与无因次周期的关系为:
(2)
其中:H*为无因次波高;T*为无因次周期;B=0.062。二者计算公式如下:
(3)
T*=gTs/u*。
(4)
其中:Hs为有效波高;Ts为有效波周期;u*为摩擦风速。
不同作者给出的拖曳系数不同[20-21],本文取Wu[22]给出的拖曳系数公式:
Cd=(0.8+0.065U10)×10-3。
(5)
图3为纯风浪,纯涌浪与Toba-3/2指数律指数率对比图。蓝色曲线为Toba-3/2指数律,红色点及曲线为纯涌浪情形,黑色点及曲线为纯风浪情形。二者分别有5 456、852个数据。曲线由最小二乘法拟合得到。纯风浪及纯涌浪能量都比Toba偏小[18],且涌浪处在风浪上方,二者分别为:
(6)
(7)
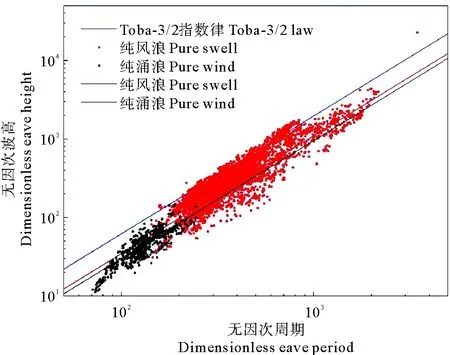
(蓝色曲线为Toba-3/2指数律;红色点及曲线为纯涌浪情形;黑色点及曲线为纯风浪情形。Blue line is Toba-3/2 law, Red line and dots represent the case of pure swell; Black line and dots represent the case of pure wind.)
图3 纯风浪,纯涌浪与Toba-3/2指数律对比
Fig.3 The comparation of pure swell, pure wind and Toba-3/2 law
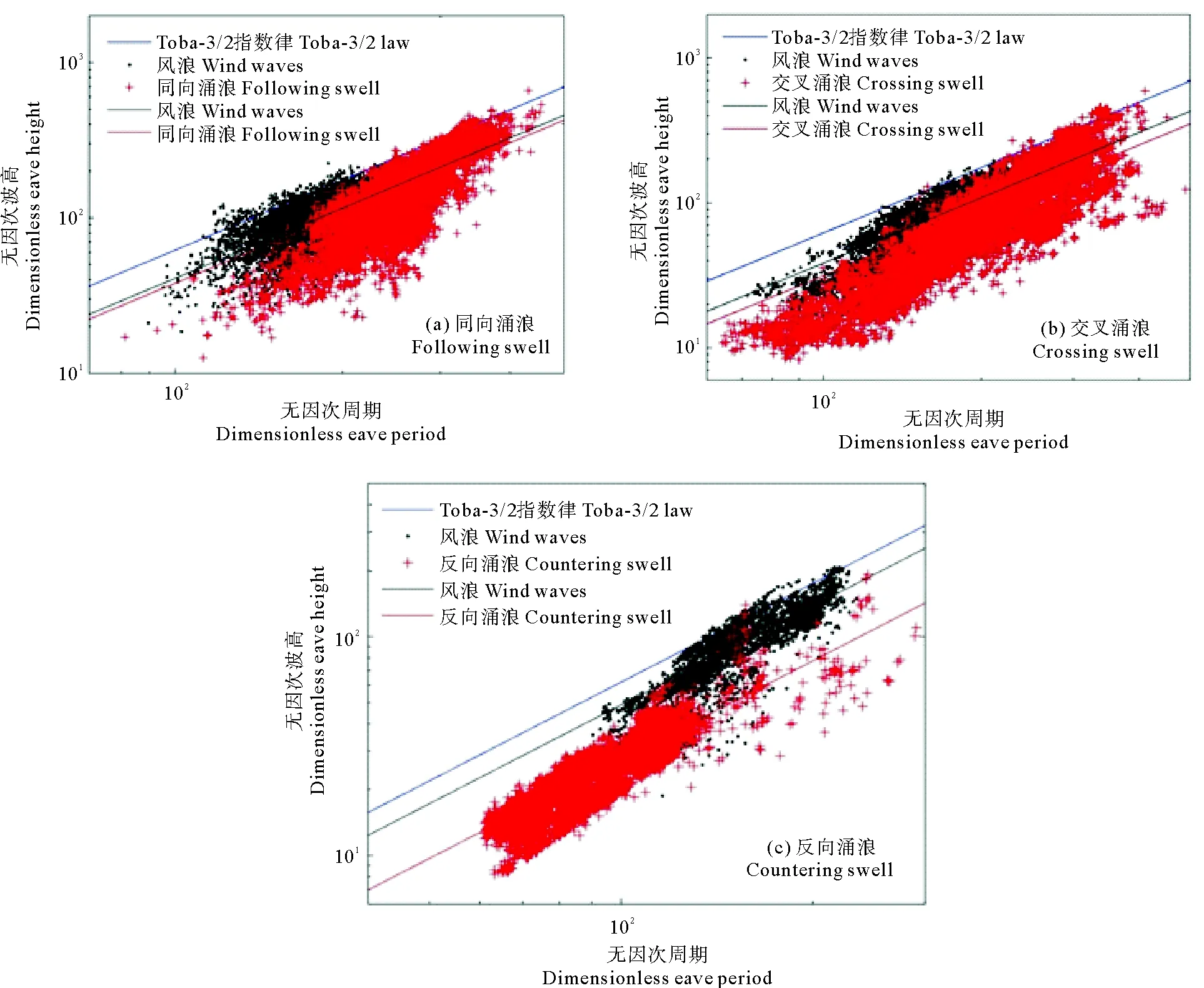
(蓝色曲线为Toba-3/2指数律;红色点及曲线为涌浪情形;黑色点及曲线为风浪情形。Blue line is Toba-3/2 law, Red line and dots represent swell; Black line and dots represent wind waves.)
图4 不同类型涌浪对风浪的影响
Fig.4 The effect of deflection angles between wind waves and swells on wind-wave
根据Sugihara等[23]分类方法,把混合海浪分为三类,风涌浪夹角小于45 ℃为同向涌浪(Following swell),大于135 ℃为反向涌浪(Countering swell),角度在二者之间为交叉涌浪(Crossing swell)。图4为按照Sugihara等[23]划分标准得到的不同类型涌浪对风浪的影响。三种情况分别有5 755、4 295、8 958个数据。图中曲线由最小二乘法拟合所得。不同类型风、涌浪结果分别为:
同向涌浪存在时,风、涌浪无因次波高与无因次周期关系分别为:
(8)
(9)
交叉涌浪存在时,风、涌浪无因次波高与无因次周期关系分别为:
(10)
(11)
反向涌浪存在时,风、涌浪无因次波高与无因次周期关系分别为:
(12)
(13)
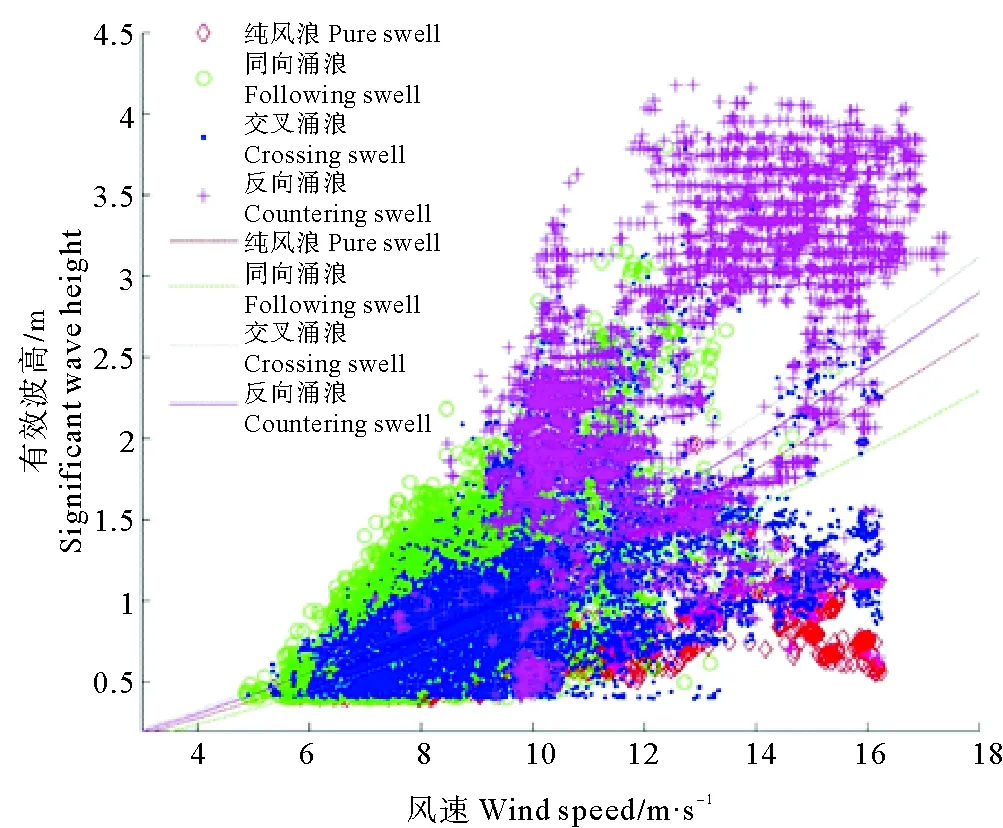
(红色菱形及虚线为纯风浪情况;绿色原型及点划线为同向涌浪;蓝色点及点线为交叉涌浪;玫红色加号及实线为反向涌浪。Red line and diamonds represent the case of pure wind; Green line and circles represent the case of following swell; Blue line and dots represent the case of crossing swell;Magenta line and plus represent the case ofcountering swell.)
图5 不同类型涌浪对风浪有效波高的影响
Fig.5 The effect of deflection angles between wind waves and swells on wind-wave significant wave height
图5为不同类型涌浪对风浪有效波高的影响。三种类型涌浪存在时,风浪有效波高都有所增加,其中尤其以反向涌浪增加最多。相应的,反向涌浪的能量也最小。与图4相一致。这与白冠覆盖率的结果相一致。在涌浪对白冠覆盖率影响的研究中,涌浪的存在抑制波浪破碎,且这种抑制与涌浪的类型没有关系[23]。众所周知,风向海洋输入能浪,驱动波浪成长,波浪成长到临界值破碎,则风输入能量主要是由波浪能量及波浪破碎构成,相同条件下,波浪破碎越小,耗散掉的能量越小,波高越大。据近年研究,涌浪主要通过两个可能机制影响风浪能量。首先,涌浪通过影响风应力输入从而影响风浪能量。风应力依赖海面粗糙度,海面粗糙度与波浪状态有关,涌浪通过调节粗糙度从而调节风应力。高风速风浪呈年轻状态时,风应力会因为涌浪存在而减小[12]。而在较低风速下,涌浪会增大粗糙度从而增加风应力,风输入能量增加,促进波浪成长[11]。其次,根据Longuet-Higgins和Stewart[3]理论,二阶近似情况下,涌浪会调节风浪振幅以及相位,造成频移。从而增大风浪能量,拓宽风浪谱。本次观测获得了大量的外海中低风速下的波浪观测数据,观测结果显示,大洋当中,普遍有涌浪存在,并且风涌浪波高较大,整体来说,涌浪向风浪传递能量。
5 结语
本文首先根据PM充分成长关系发现了测波雷达风浪的有效波高偏大,进一步发现了是由于测波雷达选择的分离判据为1D法,只使用了周期作为风、涌分离标准,风、涌浪分离判据不准确。因此,本文根据测波雷达的谱数据特征,采用2D法与1D法结合的判据,重新对风、涌浪进行了分离。通过对比不同的波龄判据,发现当波龄取1.5时,所得结果与PM谱吻合良好,因此最终采取1.5作为分离判据。
本文根据上述分离判据,计算了测波雷达共25 316个频率方向谱。以Toba-3/2定律为基础,探讨了涌浪对风浪能量的影响。发现大洋当中,涌浪的存在整体上使风浪能量增加,这种增加与涌浪的类型无关,只是在反向涌浪存在时,风浪的能量增加更多,这与破碎所得结果一致。
