广义CN环
2019-04-16魏俊潮
韩 悦,马 丽,魏俊潮
(扬州大学数学科学学院,江苏 扬州 225002)
本文中R表示有单位元的结合环,E(R),N(R),Z(R),J(R)和Lmax(R)分别表示R的幂等元集合、幂零元集合、R的中心、Jacobson根及R的全体极大左理想的集合.为研究Von Neumann正则环的强正则性,Drazin[1]引入 CN环的概念;Ungor等[2]证明CN环是中心幂零环,并讨论了 CN环与相关环类的关系;笔者[3-5]由环的交换性条件给出了CN环许多有趣的刻画,有关CN环推广的研究也较多[6-7].若环R的每个极大左理想都是R的理想,则称R是左quasi-duo环[8],文献[9-10]中给出了左quasi-duo环的很多刻画,并探讨了左quasi-duo环与相关环类之间的关系.本文拟研究广义CN环的性质,并将CN环和左quasi-duo环的相关性质推广到广义CN环上.
1 主要结论
定理1R为左quasi-duo环当且仅当对任意x,y∈R,任意M∈Lmax(R),且xy∈M,则yx∈M.
证明 (必要性) 假设xy∈M,yx∉M,则Ryx+M=R.记ayx+m=1,其中a∈R,m∈M,y=(ayx+m)y=(ay)(xy)+my. 因R为左quasi-duo环,故M为R的理想;又因xy∈M,m∈M,有(ay)(xy)∈M,my∈M,则y∈M,从而yx∈M,矛盾;故yx∈M.
(充分性) 设M是R的一个极大左理想,任取y∈R,若My⊄M,则R=My+M,记ny+m=1,其中n,m∈M.由于n∈M且M是R左理想,故yn∈M.由充分性条件知ny∈M,有1=ny+m∈M,M=R,矛盾;因此My⊆M,M是R理想,从而R为左quasi-duo环.
定理2一个环R为广义CN环当且仅当对任意a∈N(R),任意M∈Lmax(R),有Ma⊆M.
证明 (必要性) 若a∈N(R),M∈Lmax(R),使Ma⊄M,则Ma+M=R,记1=ma+n,其中m,n∈M.由于a∈N(R),存在正整数t使at=0,则ma·at-1=mat=0∈M;又因R为广义CN环,故at-1∈M或at-1ma∈M.若at-1ma∈M,有at-1=at-1(ma+n)=at-1ma+at-1n∈M,故总有at-1∈M.因ma·at-2=mat-1∈M,同理可得at-2∈M,如此重复,得a∈M,故Ma⊆M,矛盾;因此对任意a∈N(R),任意M∈Lmax(R),有Ma⊆M.
(充分性) 设x∈R,a∈N(R),M∈Lmax(R)满足xa∈M.若ax∈M,得证. 若ax∉M,则Rax+M=R,记rax+m=1,其中r∈R,m∈M,则a=(rax+m)a=(ra)(xa)+ma.由xa∈M,得(ra)(xa)∈M,因ma∈Ma⊆M,故a∈M;因此R为广义CN环.
众所周知,一个环R是左quasi-duo环当且仅当R/J(R)是左quasi-duo环.关于广义 CN环,由定理2可得推论3.
推论3若R/J(R)是广义CN环,则R为广义CN环.
尚不清楚推论3的逆命题是否成立.
定理4广义CN环R为直接有限环.
证明 设a,b∈R,满足ab=1.记e=ba,h=(1-e)a,则ae=aba=a,h2=0.下证h∈J(R),否则存在M∈Lmax(R)使得h∉M,则Rh+M=R.记xh+m=1,其中x∈R,m∈M,有h=(xh+m)h=xh2+mh=mh∈Mh.由R为广义CN环及定理2知,Mh⊆M,则h∈M,矛盾;故h∈J(R),hb∈J(R).又hb=(1-e)ab=1-e,得1-e∈J(R),则e=1-(1-e)是R的可逆元;由(1-e)e=0,得1-e=0,故ba=e=1,从而R为直接有限环.
定理5R为广义CN环当且仅当N(R)⊆J(R).
证明 (必要性) 若N(R)⊄J(R),则有a∈N(R),使得a∉J(R),故有R的极大左理想M,使a∉M,则Ra+M=R,记ba+m=1,其中b∈R,m∈M.设n≥1,使an=0,有an-1=(ba+m)an-1=ban+man-1=man-1,由R为广义CN环和定理2知man-1∈Man-1⊆M,则an-1∈M;又因an-2=(ba+m)an-2,同理得an-2∈M,如此重复,得a∈M,矛盾,故N(R)⊆J(R).
(充分性) 对任意a∈N(R),任意M∈Lmax(R),有Ma⊆MJ(R)⊆J(R)⊆M,由定理2可知R为广义CN环.
文献[11]中将N(R)⊆J(R)的环R称为J-约化的,由定理5知J-约化环就是广义CN环.
推论6设R为广义CN环,e2=e∈R,则eRe为广义CN环.
推论7设e是环R的中心幂等元,若eRe,(1-e)R(1-e)为广义CN环,则R为广义CN环.
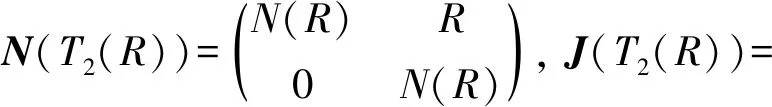
定理9R为广义CN环当且仅当T2(R)为广义CN环.
证明 (必要性) 由R为广义CN环和定理5知N(R)⊆J(R),由引理8知N(T2(R))⊆J(T2(R)),则T2(R)为广义CN环.
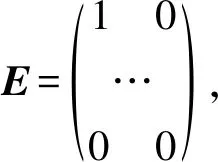
利用定理9及数学归纳法,可得下列推论.
推论10R为广义CN环当且仅当R上的n阶上三角矩阵环Tn(R)为广义CN环.
引理11设S是环R的子环,则J(R)∩S⊆J(S).
命题12设S是环R的子环,若R为广义CN环,则S为广义CN环.
推论13R为广义CN环当且仅当V2(R)为广义CN环.
证明 (必要性) 这是定理9和命题12的直接推论.

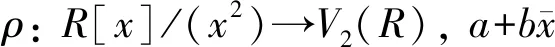
推论14R为广义CN环当且仅当R[x]/(x2)为广义CN环.
推论15R为广义CN环当且仅当GT3(R)为广义CN环.
定理16R为直接有限环当且仅当对任意a∈Ur(R),M∈Lmax(R),有a∉M.
命题17设I是环R的理想且I⊆J(R),若R/I为广义CN环,则R为广义CN环.
推论18设I是环R的幂零理想,则R为广义CN环当且仅当R/I为广义CN环.
推论19设I是环R的理想,则R/I为广义CN环当且仅当R/I2为广义CN环.
