一种基于极化码APC-SCL的译码算法
2019-04-15李君玉王淑琴刘东海
李君玉, 王淑琴, 刘东海
(1. 中北大学 电子测试技术国家重点实验室, 山西 太原 030051;2. 中北大学 仪器科学与动态测试教育部重点实验室, 山西 太原 030051)
0 引 言
2008年, 土耳其教授Erdal Arikan最先提出极化码这一概念, 它是第一种被证明了能够在二进制离散无记忆信道下达到香农限的码, 同时也被确定为5G eMBB场景下控制信道编码, 被广泛应用于各个领域, 尤其是通信领域[1].
对于通信系统来说, 编码和译码算法都是其研究的核心的内容. 极化码编码选择质量好的信道传输信息比特, 选择质量差的信道传输固定比特, 其编码方案依照信道极化的规则来进行变换. 在译码方面, Arikan给出了极化码的串行抵消(Successive Cancellation)译码算法[2]. I.Tal提出了基于SC译码算法的list算法[3], 也就是SCL算法, SCL算法具有接近最大似然的性能, 所以被广泛使用, 但由于继承了SC算法的思想, 延迟高的问题并没有得到解决, 并且复杂度较高[4]. 本设计在CRC-SCL算法的基础上进行改进, 形成一种新的译码算法, 即APC-SCL(Adaptive Partitioned CRC-SC List)译码算法, 极化码编码时, 对信息比特分组, 并在每组信息比特的后面增加监督位. 译码时, 先进行SC译码, 再根据校验信息选择, 得到最后的译码结果.
1 CRC-SCL译码算法
CRC是常见的辅助校验手段, 广泛用于数据通信与网络中. CRC-SCL译码即为在极化码的SCL译码算法中加入 CRC监督位, 改进的SCL译码算法性能大大提升[5], 同时编码速率并没有减少太多, 两者处于一种比较平衡的状态. CRC-SCL编译流程如图 1 所示.

图 1 CRC-SCL算法通信框图Fig.1 Communication diagram of CRC-SCL algorithm
算法的基本思想为: 输入k比特的信息位, 然后添加m位CRC码, 将K=k+m比特输入编码器[6], 对信息位进行极化码编码, 得到N位信道输入, 经过添加噪声后的信道(例如高斯白噪声信道等)传输进入译码器. 该译码器包含SCL译码器和解CRC码单元. SCL译码器译出L个候选序列之后, 将其对应的路径度量值进行由大到小的排序, 输出最有效的路径结果. 发端和收端使用一致的CRC多项式g(X), 根据CRC校验和是否为0判断传输过程有无发生错误[7]. CRC-24条件下
g(x)=x24+x23+x18+x17+x14+x11+x10+
x7+x6+x5+x4+x3+x+1.
(1)
选取MATLAB平台对CRC-SCL译码算法进行仿真, 仿真条件如表 1 所示,
图 2 所示为极化码在不同列表长度CRC-SCL算法下的误帧率比较, 表 2 为CRC-SCL译码算法平均搜索宽度.

表 1 仿真条件Tab.1 Simulation condition

表 2 CRC-SCL译码算法平均搜索宽度Tab.2 The mean of search width of the CRC-SCL decoding algorithm
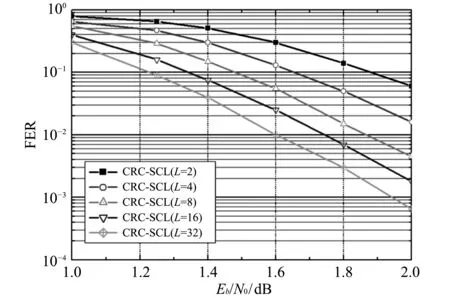
图 2 极化码在不同列表长度CRC-SCL算法下 的误帧率性能对比图Fig.2 Frame error rate comparison of CRC-SCL algorithm under diffent list length
仿真表明, 极化码的CRC-SCL译码算法可以通过增大列表长度的方式获得译码性能的持续提升, 而且列表长度越大, 所获得的性能增益也越大[8]. 例如, 当FER性能为10-2时, 列表长度为32和8所需的信噪比分别为1.60 dB和1.87 dB, 性能增益提升了0.27 dB. 由表 2 可看出: CRC-SCL译码平均搜索宽度随着信噪比的增大而减小, 可见, CRC-SCL译码算法在高信噪比区间性能较好、 译码复杂度较低; 在低信噪比区间性能较差、 译码复杂度较高.
2 APC-SCL译码算法
通过分析CRC-SCL译码算法, 发现其译码复杂度随信噪比减小而增大, 在低信噪比区间的性能不理想, 所以提出自适应性分段循环冗余校验辅助串行抵消列表(APC-SCL)译码算法[9].
图 3 所示为算法编译框图.

图 3 APC-SCL算法编译框图Fig.3 Compilation diagram of APC-SCL algorithm
2.1 编码结构
APC-SCL算法在编码时采用分段编码[10], 不仅在性能上与CRC校验能实现同样的效果, 而且在结构上易于实现.
算法的基本思想是: 首先确定分段的数量, 然后根据信息位和监督位的制约关系, 确定监督位位数, 在每个子段信息比特后增加监督位, 最后将子段序列拼接起来再进行极化码的编码[11].
在确定分段P时, 需要考虑如下的制约关系:
假设码长为N, 其中K个位置上传输来自信源的消息比特, 剩余的N-K的位置传输不含信息量的固定比特, 码率R=K/N,K为有用比特数, 分为P组, 则每组K/P个比特,K/P=k+C.k和C必须满足2C≥k+C+1,k是信息比特的位数,C是CRC监督位的位数. 随着P的增加, CRC-SCL译码算法的编码效率会变小, 为保证传输的码率不变, 应考虑每段CRC的位数CP, 也就是C/P的关系,CP越小, 校验性能越差, 漏检率越高, 译码性能降低[12].
2.2 译码结构
译码时对该段先采用SC译码, 如果校验成功则进行下一段译码; 如果校验失败, 则对该段进行SCL译码, 同时将搜索宽度直接赋值为最大搜索宽度, 减少译码时间. 如果可以通过CRC校验, 则进行下一段译码, 否则校验失败.
以P=1为例, 假如每个时钟为1个周期, CRC-SCL译码算法完成译码需要2N-2+RN个时钟, 但SC译码算法完成译码仅需要2N-2个时钟周期[13].
改进后的译码算法, 初始化时i=1,L=1, 先走SC算法译码, 进行CRC校验, 当译码不成功时不再逐渐增大L, 而是直接令L=Lmax, 走SCL译码算法, 进行CRC校验, 完成译码[14]. 改进后的译码算法最大搜索宽度不变, 译码性能不受影响. 译码器在SC和SCL两种译码模式下切换, 完成译码工作. 大部分码字可以用2N-2个时钟完成译码, 很少一部分会需要(2N-2)+(2N-2+RN)=4N-4+RN个时钟, 随着信噪比的增高, 译码周期平均值趋于2N-2. 具体译码流程如图 4 所示.

图 4 APC-SCL译码算法流程图Fig.4 The flow chart of APC-SCL decoding algorithm
3 仿真结果与分析
仿真基于MATLAB平台, 取码长为1 024, 列表长度统一设置为32, 分别对P取不同值的APC-SCL算法译码性能进行分析, 仿真配置见表 3. 由于在码长为1 024时, 分成32组和64组, 编码效率η分别为68.75%和50%, 由于这两种分段方式的编码效率太低, 因此这两种分组不予考虑.
由图 5 的仿真结果可看出, 在码长为1 024条件下, 误帧率为10-2,P=16时APC-SCL译码算法相比CRC-SCL译码获得了0.1 dB的增益, 随着信噪比的增加, 误帧率逐渐降低, 在大信噪比下, 优异性更加明显. 由于过多的分组会导致编码效率降低, 大量的监督比特会占用可靠信道, 降低信息比特数量[15]. 综合硬件条件, 取P=2或P=4都是不错的选择. 由于CRC-SCL算法编码效率为95%, 所以本译码算法选择P=2,
图 6 为APC-SCL算法和CRC-SCL算法在不同列表长度下的误帧率比较. 表 4 为APC-SCL译码算法平均宽度.

表 3 仿真参数Tab.3 Simulation parameterR

图 5 不同P值下的FER比较Fig.5 Comparison of FER under different P values
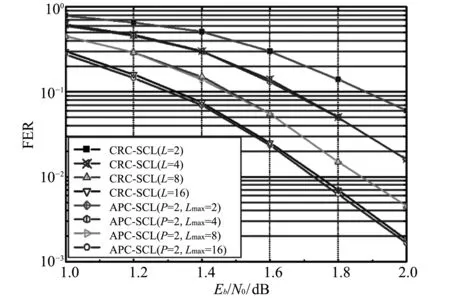
图 6 极化码在APC-SCL和CRC-SCL算法下的FER比较Fig.6 Comparison of FER of polarization codes under APC-SCL and CRC-SCL algorithms
从图 6 的对比中可以看出: APC-SCL译码算法相对于CRC-SCL译码算法基本无性能损失, 曲线走向一致, 随着搜索宽度L的增加, 分两段APC-SCL译码逐渐和CRC-SCL译码拉开差距, 而且在不同误帧率的情况下, 均获得了0.05~0.1 dB 的增益. 对比表 2 和表 4 中的数据, 可以得到改进的算法相对于之前的译码算法平均搜索宽度减少的百分比,
图 7 所示为不同信噪比之下两种译码算法的平均搜索宽度减少的百分比. 结合图表可以分析出APC-SCL译码算法在低信噪比区间平均搜索宽度减小了26.8%, 译码复杂度减小.
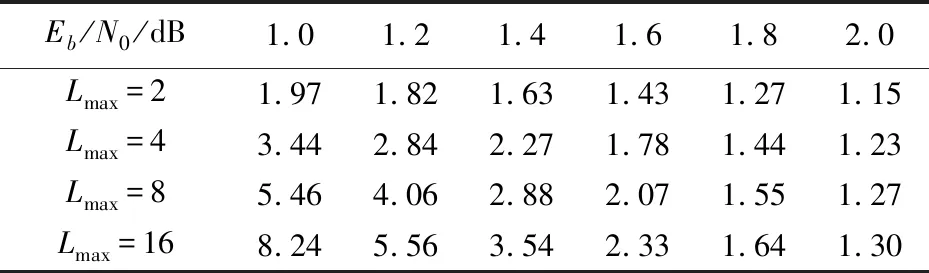
表 4 APC-SCL译码算法平均搜索宽度Tab.4 The mean of Search width of the APC-SCL decoding algorithm

图 7 APC-SCL算法相对于CRC-SCL算法平均 搜索宽度减少百分比Fig.7 The average search width reduction of APC-SCL algorithm compared to CRC-SCL algorithm
着眼于译码复杂度, 本文的设计比现有技术更加的简便. 使用所提出的分段编码, 降低了译码的空间复杂度, 而自适应的译码算法则降低了原有译码的时间复杂度.
4 结束语
本文提出的APC-SCL极化码译码算法, 通过仿真分析, 在降低译码复杂度上明显优于CRC-SCL译码算法, 在同等条件下, 能够降低算法在低信噪比区间的平均搜索宽度. 关于列表长度与监督位, 增加监督位比特的确会使纠错能力增强, 但同时也会降低极化码的编码效率; 增加列表长度的确会使算法性能更加优良, 但是过大的列表长度会带来更大的复杂度以及延迟等问题, 如何在两者之间取得平衡也是接下来需要研究的问题.
