SPMT双纵列车板运输稳定性及运输能力分析

徐学军

(海洋石油工程(青岛)有限公司，山东 青岛 266520)

SPMT(Self-propelled modular transporter)模块车作为特种运输设备，具有载重量大、运动灵活的优势，主要应用于重型和超大型结构物的运输，在港口码头大件滚装、装备制造业、海洋石油、化工、桥梁建造等工程领域应用广泛[1-4]。一般情况下，SPMT通过车板的横向及纵向拼接形成车组用于大件货物的运输。但在某些情况下，也会用到双纵列(单挂)车板进行运输作业。区别于大规模车组作业，单挂车运输的稳定性及车板运输能力需要特别留意。本文通过稳定性计算及车货系统力学计算对SPMT模块车双纵列车板的运输稳定性及运输能力进行了分析。

1 运输稳定性

1.1 支撑方式的选择

三点支撑方式能保证形成一个确定的支撑系统，且对被运输货物的整体结构强度要求相对较低，所以多挂车运输时优先使用三点支撑方式。双纵列(单挂)车板在三点支撑与四点支撑方式下的稳定性对比见图1，可见在被运物重心发生相同偏移的情况下，四点支撑方式下重心距离倾覆线的距离要比三点支撑方式大得多。所以对于双纵列车板的运输作业宜采用四点支撑的编点方式。

1.2 静态稳定性计算原理

由于货物在运行中已与车体牢固捆扎，在SPMT车货系统受到外部因素影响而发生横向失稳时，车货系统是以挂车悬挂摆臂纵轴为侧翻支点的(见图2)。因此稳定性计算中的重心应是车辆和货物的组合重心。车货系统组合重心与悬挂摆臂纵轴的连线与垂直线的夹角即为静态稳定角[5]，静态稳定角越大，运输稳定性越好。静态稳定角的计算公式为：

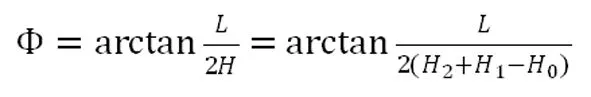
(1)

其中，L为悬挂摆臂纵轴间距，为定值；H0为悬挂摆臂纵轴离地高度，为定值；H1为SPMT车板上表面离地高度，该值可在1250mm～1750mm之间变化；H2为车货系统重心与SPMT车板上表面的垂直高度，此处按定值考虑；H为计算重心高度，H=H1+H2-H0。

通过公式(1)可以发现，计算重心高度H是影响车货系统行驶稳定性的主要因素，车货系统重心高度越低，运输稳定性越好。同时，在形式过程中车板高度是变化的，车板高度越大，运输稳定性越差。在校核双纵列车板运输稳定性时，保守起见应在车板高度最高的情况下计算运输稳定性。

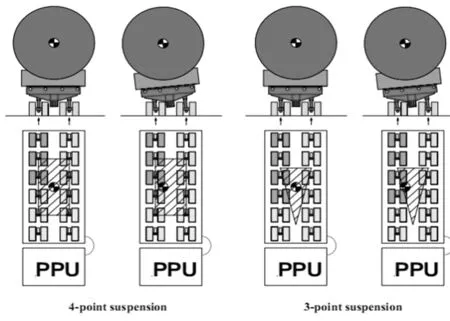
图1 三点支撑与四点支撑稳定性对比

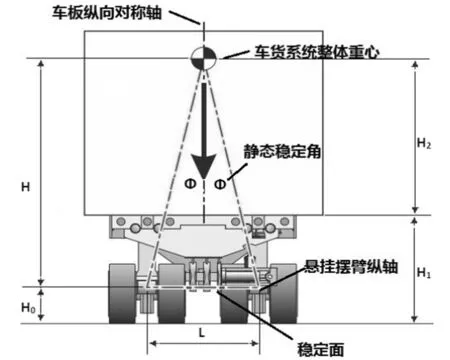
图2 车货系统静态稳定角计算原理

2 货物重量与货物载荷作用位置的关系

2.1 车货系统力学计算模型

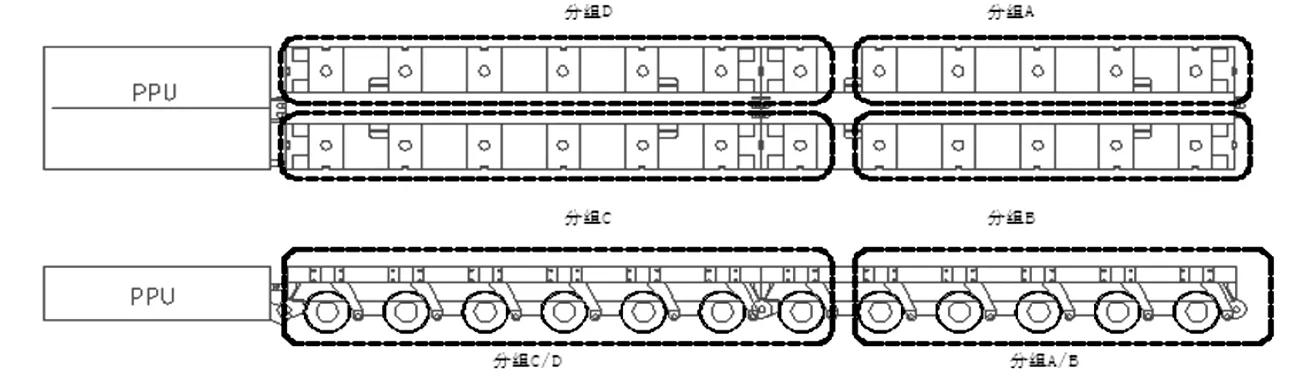
图3 m=12，n=5时的编点分组方式

假定地面基本平整，忽略压力沿地面方向的分量，仅考虑垂向分量。按矩形四点支撑进行编点分组，对于m轴线车板，若分组A/B中轴线数量为n，则分组C/D中轴线数量为m-n，n取1～(m-1)。图3为m=12，n=5时的编点分组示意图。

取SPMT车板上表面最前端位置为坐标原点，建立如图4所示坐标系。其中，分组A/B中地面对轴线的反力为P1、分组C/D中地面对轴线的反力为P2、货物重量G与车板前端距离为L、PPU重量为f1，其与车板后部边缘的距离为L’。

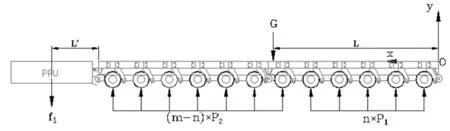
图4 以m=12为例，车板地面反力计算简图

车板轴线间距尺寸参见图5。

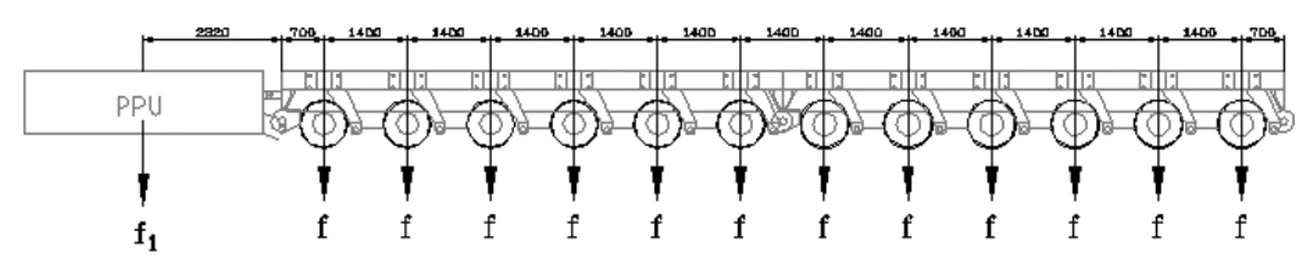
图5 以m=12为例，车板自重及尺寸

将分组A/B承受的地面反力与车板自重之差记为F ’1，分组C/D承受的地面反力与车板自重之差记为F2，可知，

(2)

并将PPU载荷移至车板的末端，得到图6所示的计算模型。

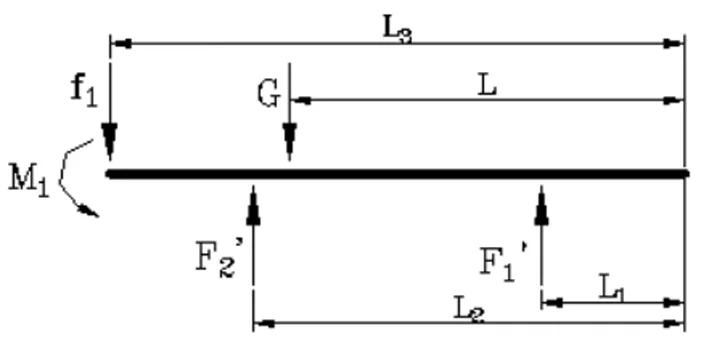
图6 车板举升力学计算模型

分别在车板前后两端取矩，得到力矩平衡方程如下：

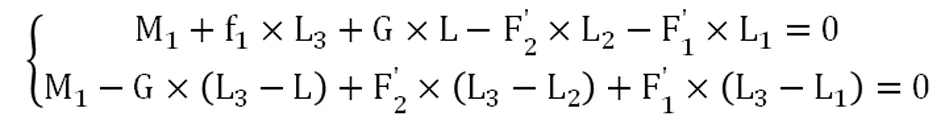
(3)

分组A/B几何中心与车前部距离L1、分组C/D几何中心与车前部距离L2、车板总长度L3分别为：

(4)

将(4)带入(3)，并求解可得：

(5)

由(2)及(5)可得地面对分组A/B轴线的反力P1、地面对对分组C/D轴线的反力P2分别为：

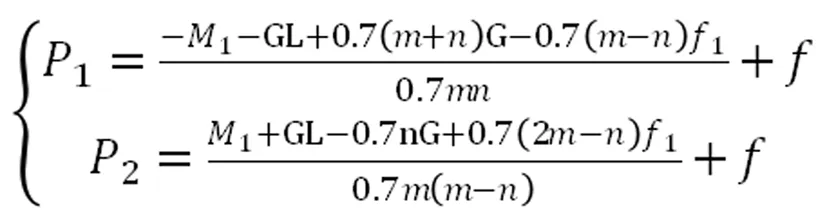
(6)

其中，PPU的自重：f1=7.2吨，PPU重心与车板尾端距离：L’=2.32米，PPU施加于车板尾端的力矩：M1=f1L’=7.2×2.32=16.704吨米，车板折算到每个轴线上的自重：f=4.3吨，四者均为定值，带入(6)可得：

(7)

由(7)可知，不同分组车板轴线承受的地面反力取决于车板数量m、编点方式n、货物重量G和货物在车板上的位置L。

2.2 车货系统满足要求的判定准则

SPMT每个轴线可承受的载荷是有上限的，对于德国索埃勒公司生产的实心轮胎SPMT车板，每轴线最大可承受48t的载荷。同时，不同分组之间的支撑液压差最大不超过50bar，即不同分组之间轴线载荷之差最大不超过9t。

同时，地面对轮胎的反力P1、P2均需大于0t。这是因为假若其中一个参数等于0，则说明此时车板中只有两个分组承受载荷，而两点支撑是不稳定的，车板必定发生纵向的倾斜。

据此，可以得到车板举升能力满足要求的判定准则：

(8)

其中μ为安全系数，此处取为0.7。

2.3 不同编点方式下许可的货物载荷作用范围

对于6轴线车板，分别令公式(7)中的，可得到6轴线车板全部5种编点方式下不同分组内轴线承受的地面反力P1、P2，之后将该两数值带入判别准则(8)中，即可得到不同编点方式下许可的货物载荷范围及大小。考虑6轴线车板仅在n=3、n=4两种编点方式下满足空载行驶的要求，所以此处进分析在该两种编点方式下许可的货物作用范围及大小。

n=3时判别准则形式为：

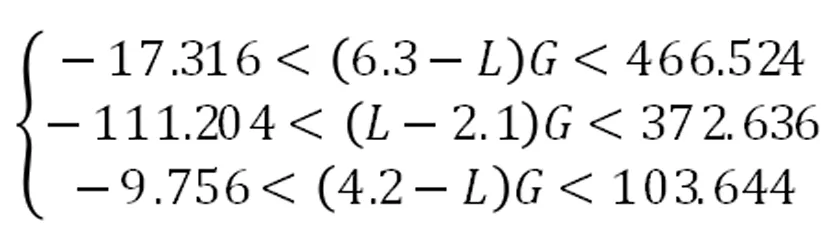
(9)

n=4时判别准则形式为：

(10)

上两式实际为含有G和L两个变量的不等式组，在货物重量G和作用位置L均满足该3个不等式的情况下，满足6轴线车板运输稳定性要求。

图7为6轴线车板在n=3、n=4两种编点方式下G和L两个变量的关系，其中阴影区域为许可的货物载荷大小及作用范围。可见判定准则中的0<│P1-P2│<9对货物载荷大小及作用范围起到主要影响。同时，当货物重心与车板前端距离在3.7～4.2m之间时，车板承载能力较强，达到170T以上，为最佳放置位置；当货物重心与车板前端距离超过4.2米或小于3.7米时，车板承载能力急剧减小，装载时应避免该种情况。

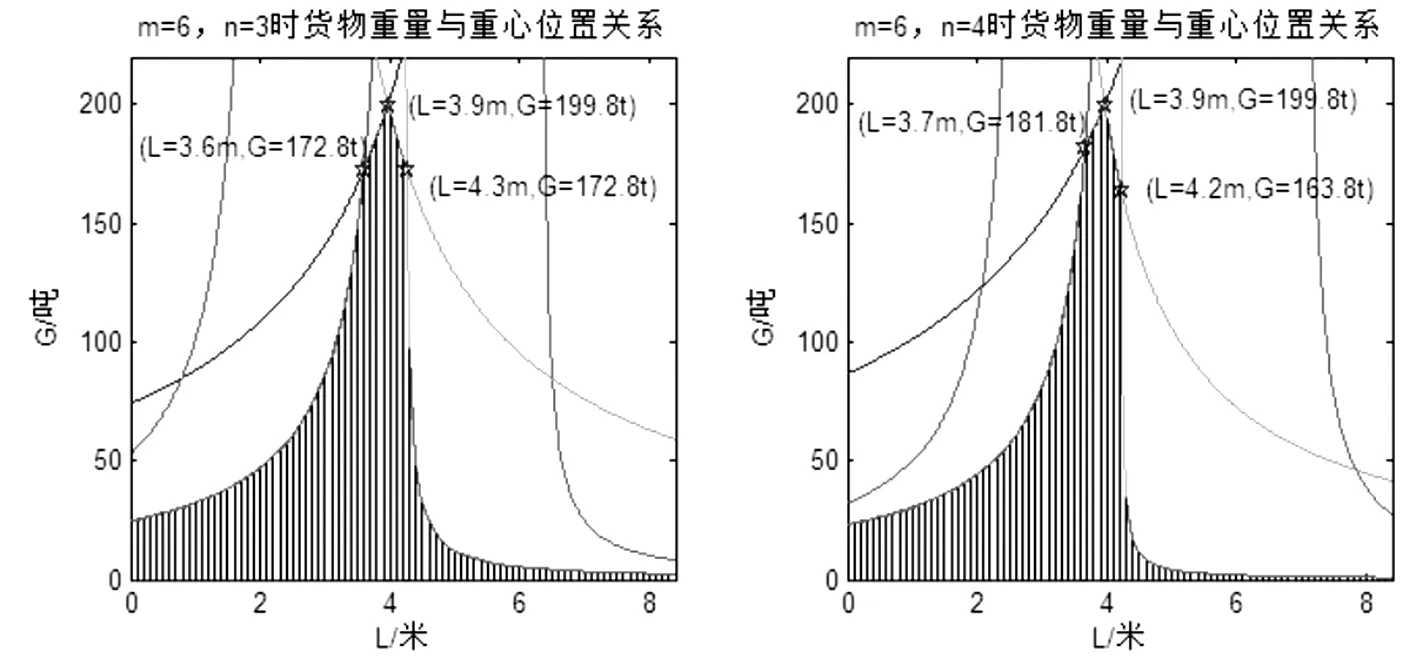
图7 6轴线车板n=3及n=4时G与L的关系

采用相同的方法，可得到如图8所示的12轴线车板在n=5(5-5-7-7)及n=7(7-7-5-5)两种编点方式下货物重量与货物载荷作用位置的关系。同样18轴线车板在n=8(8-8-10-10)、n=9(9-9-9-9)、n=10(10-10-8-8)三种编点方式下货物重量与货物载荷作用位置的关系，见图9。

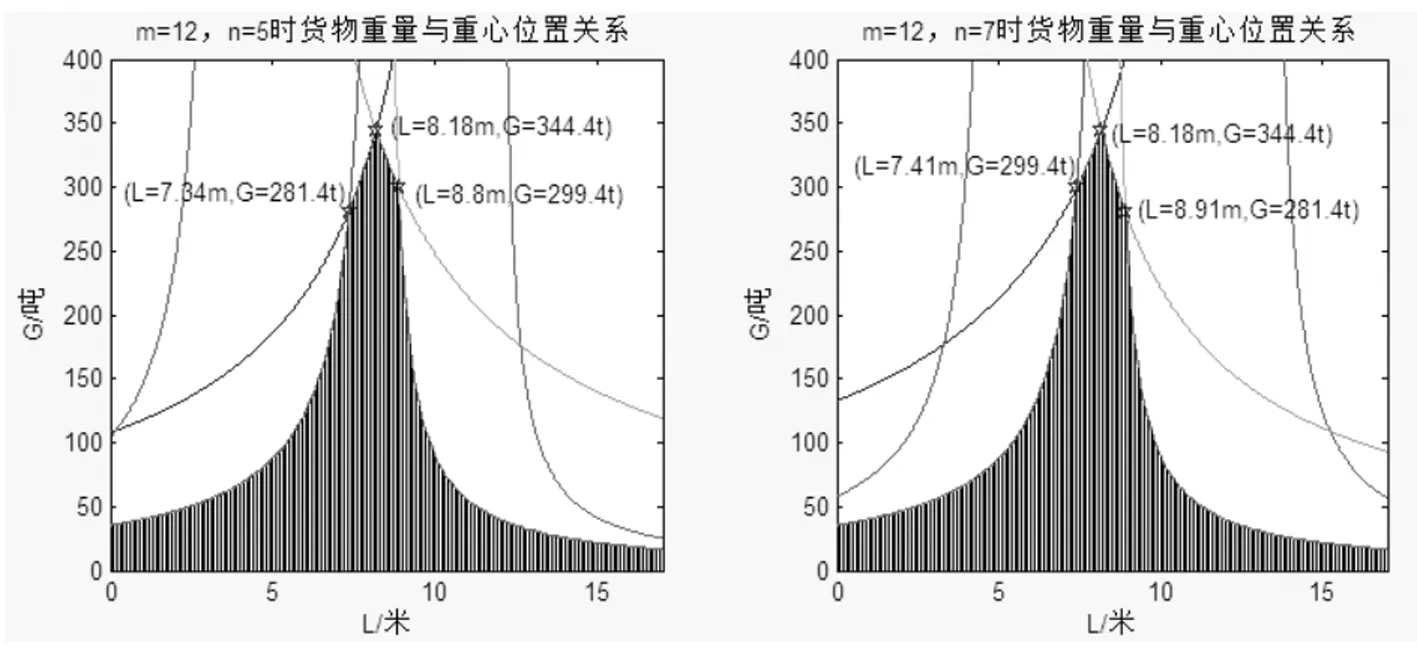
图8 12轴线车板n=5及n=7时G与L的关系

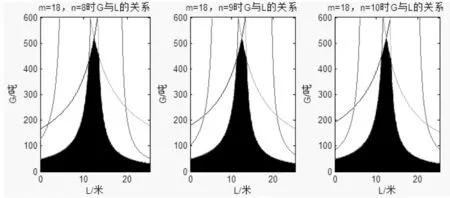
图9 18轴线车板n=8、9、10时G与L的关系

可见，对于12轴线车板，在n=5(5-5-7-7)及n=7(7-7-5-5)两种编点方式下，货物重心与车板前端距离在7.4～8.8m之间时，车板承载能力最强，为货物最佳放置位置，当货物重心超出该范围内时，车板承载能力急剧减小；对于18轴线车板，在n=8(8-8-10-10)、n=9(9-9-9-9)、n=10(10-10-8-8)三种编点方式下，许可的货物载荷位置及重量大小区别不大，货物重心距离车板前端最佳范围为11.1～13.5m。

3 结论

针对SPMT双纵列车板运输稳定性差，对货物摆放位置敏感的问题，建立了双纵列车板运输稳定性计算及车货系统力学计算模型，得到了横向稳定性计算方法及货物重量与货物载荷作用位置的关系。指出车货系统重心高度越低，运输稳定性越好，同时应在车板高度最高的情况下计算运输稳定性；SPMT车板承载能力受货物摆放位置影响较大，尽量采用均分的编点方式，货物应尽量放置在车板居中位置。