混合链式液压调平机构的动力学特性

康辉梅，朱建新，王石林



混合链式液压调平机构的动力学特性

康辉梅1，朱建新2，王石林2

(1. 湖南师范大学 工程与设计学院，湖南 长沙，410081；2. 中南大学 机电工程学院，湖南 长沙，410083)

为了研究混合链式液压调平机构的举升能力和调平能力等动力学性能，对举升过程中作平动的工作平台的欧拉角微分表达式和变分表达式进行改写，基于拉格朗日法建立调平机构的动力学数学模型，其过程包括采用复数矢量法建立各刚体质心速度方程、推导调平机构的动能方程、基于虚功原理推导调平机构的广义力方程、推导各液压油缸驱动力的动力学解析解。利用MATLAB软件对所建数学模型进行工程实例仿真，分析不同负载下3个液压油缸的驱动力，并对仿真结果进行试验验证。研究结果表明：自动液压油缸驱动力和从动液压油缸驱动力与变幅液压油缸驱动力相比对负载变化更敏感；自动液压油缸驱动力和从动液压油缸驱动力的相对大小由两者的缸筒内径和活塞杆直径决定，所建立的各液压油缸驱动力的解析解既可用于工程设计计算和分析，也可用于机构优化设计。

调平机构；动力学分析；拉格朗日法；混合链；MATLAB软件

液压调平机构是广泛应用于电力、通信、机场和消防等领域的高空作业机械[1]和主要应用于物流领域的伸缩臂叉装车[2]关键机构，其主要功能是在举升人或重物的同时保证载人或重物的工作平台恒水平，其举升能力和调平能力直接决定了整机的安全性、精确性、快速响应性等工作性能。根据不同的运动链，液压调平机构分为开链式[3]和混合链式[4]共2种，其中混合链式液压调平机构(简称为调平机构)因能提供更好的运动学和动力学性能而获得广泛应用。调平机构的举升和调平性能直接取决于各液压油缸的驱动力。王石林等[5−6]基于牛顿—欧拉法建立了调平机构的数学模型，采用MATLAB软件对各油缸驱动力进行了仿真分析；闫洪峰等[7−9]利用ADAMS软件建立了调平机构的动力学仿真模型，对各油缸驱动力进行了仿真分析。但这2种方法均只能获得各液压油缸驱动力的数值解，为了推导其解析解，必须基于拉格朗日法进行动力学数学建模。目前，基于拉格朗日法的机构动力学建模与分析主要集中在闭链机构[10−13]和开链机构[14−15]两方面，而针对混合链机构进行的动力学建模与分析较少。为了获得调平机构各液压油缸驱动力的解析解，以用于工程设计计算和分析以及进一步对机构进行优化设计，本文作者基于拉格朗日法建立调平机构的动力学数学模型，推导各液压油缸驱动力的解析解，利用MATLAB软件进行工程实例仿真分析，并与试验结果进行对比验证。

1 调平机构的结构组成及工作原理

调平机构是1个由5个构件组成的自由度为2的机构，其示意图如图1所示。机架和臂架构成1个开链机构，其中的臂架又与摇杆、连杆、工作平台一起构成1个闭链机构，以上5个构件一起构成1个自由度为2的混合链五杆机构，2个原动件分别为臂架和摇杆。调平机构工作原理如下：臂架在变幅液压油缸作用下绕点转动，带动摇杆、连杆和工作平台一起转动，实现工作平台举升；安装在臂架和摇杆之间的从动液压油缸动作，带动摇杆绕点摆动，通过连杆带动工作平台转动，使工作平台调平。当臂架转动以调节工作平台高度时，工作平台水平角度将随之改变。因此，在举升过程中，为了保持工作平台恒水平，在机架和臂架之间安装1个自动液压油缸，自动液压油缸和从动液压油缸的无杆腔与无杆腔相连、有杆腔和有杆腔相连，形成2个封闭液压回路。当臂架在变幅液压油缸的作用下绕点逆时针方向旋转时，自动液压油缸受拉伸长，其有杆腔的液压油被压缩至从动液压油缸的有杆腔中，从动液压油缸受压缩回，通过摇杆、连杆带动工作平台绕点顺时针方向旋转，自动调节工作平台至水平状态，从而保证工作平台恒水平。

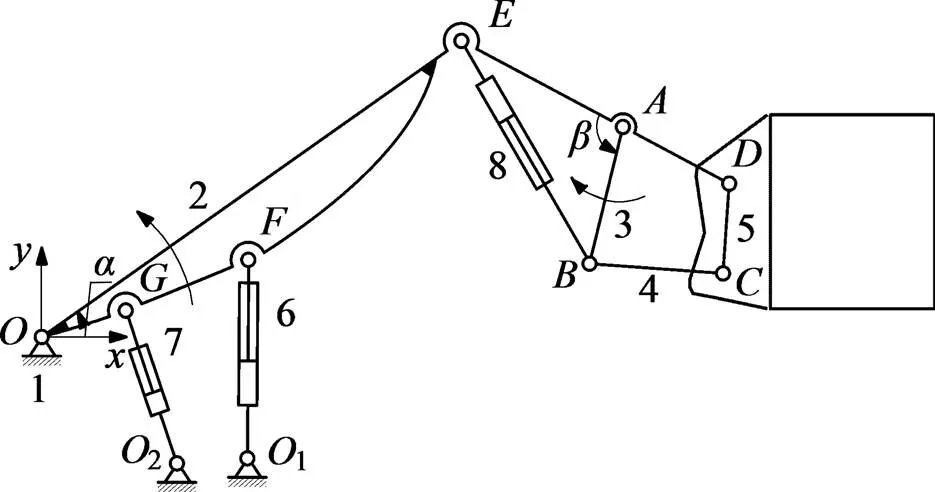
1—机架；2—臂架；3—摇杆；4—连杆；5—工作平台；6—变幅液压油缸；7—自动液压油缸；8—从动液压油缸。

2 调平机构动力学数学模型的建立

调平机构与一般混合链式机构相比具有特殊性。为了保持工作平台恒水平，在举升过程中工作平台需作平动，则工作平台的欧拉角始终保持为某一常值。采用拉格朗日法建立动力学模型时，需对各运动构件的欧拉角进行微分和变分计算。工作平台欧拉角为常值，其微分和变分均等于0，这对动力学建模产生以下2个方面的影响：1) 工作平台欧拉角的微分等于0，导致工作平台及加之于其上的重载荷的动能对各液压油缸驱动力的影响无法正确计算；2) 工作平台欧拉角的变分等于0，导致工作平台及加之于其上的重载荷重力对各液压油缸驱动力的影响无法正确计算。调平机构在举升过程中，工作平台欧拉角为常值，但从机构的运动传递来看，该常值是2个原动件共同作用的结果。因此，为了正确建立调平机构的动力学数学模型，将工作平台欧拉角的微分和变分分别改写为2个广义坐标的微分和变分的函数。

2.1 各刚体质心速度方程的建立

调平机构的自由度为2，分别选取臂架和水平面之间的夹角(称为臂架转角)以及摇杆和臂架之间的夹角(称为摇杆转角)为广义坐标。臂架、摇杆、连杆和工作平台一起构成1个封闭矢量多边形(见图2)，可得

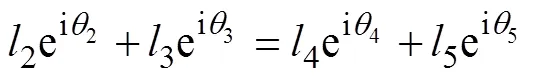
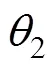
对调平机构进行运动学分析[16]可分别求得摇杆质心3、连杆质心4和工作平台质心5的速度：

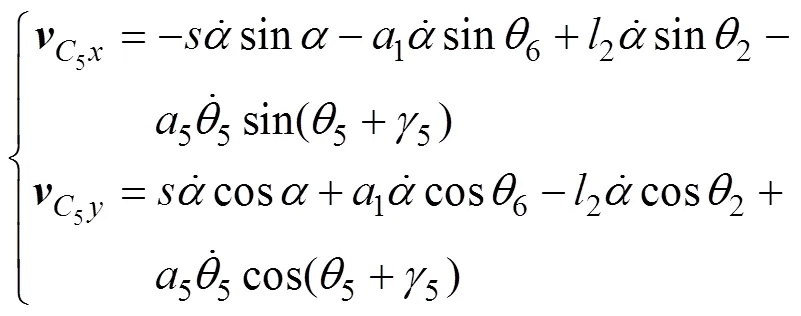
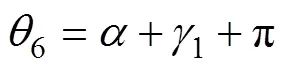
2.2 调平机构动能方程的建立

调平机构共有4个活动构件，除了臂架绕定轴转动外，其余3个活动构件(摇杆、连杆和工作平台)均作平面运动。调平机构的动能为

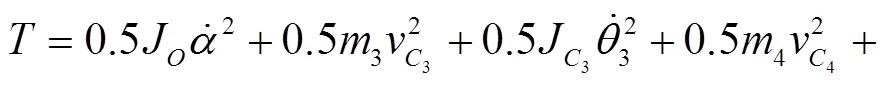
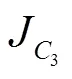
式中：

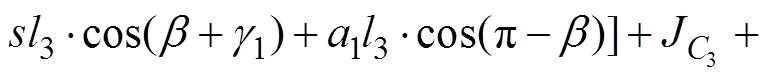
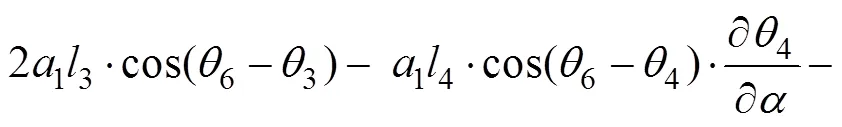
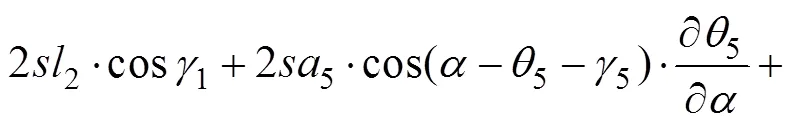
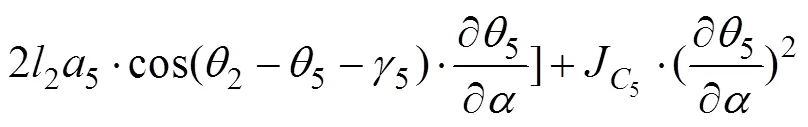
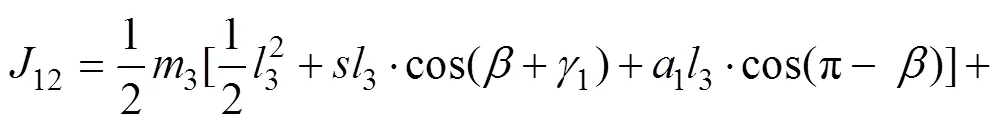
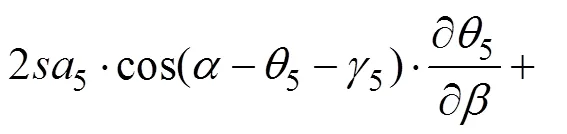
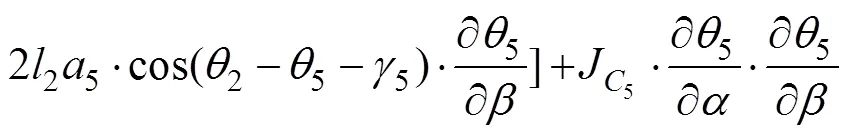
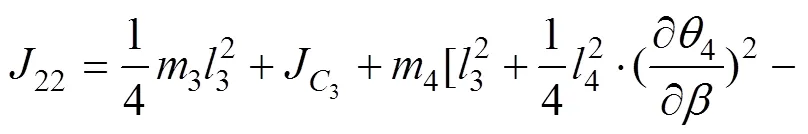
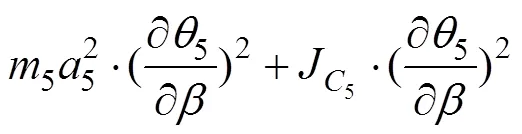
2.3 广义力方程的推导

调平机构受力情况如图3所示。

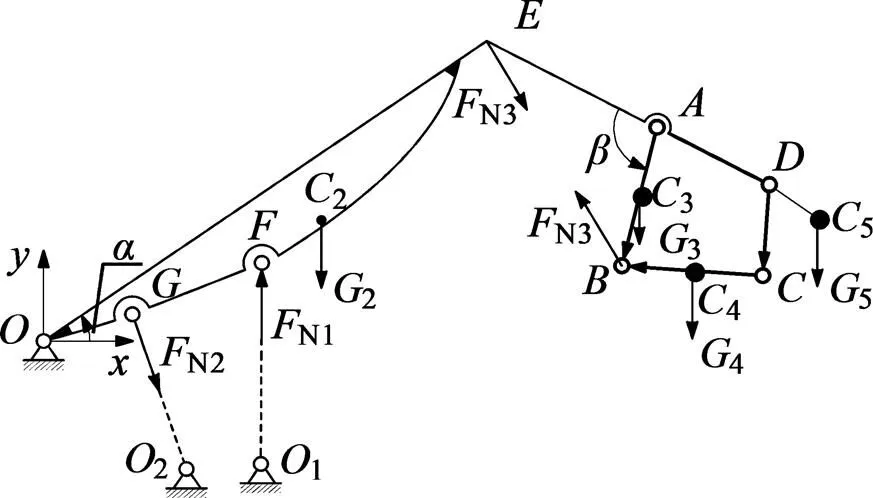
图3 调平机构受力图

调平机构中所有主动力在相应的虚位移中所作虚功的和为

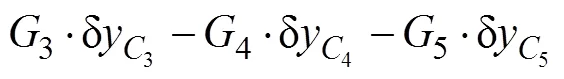
由式(10)可求得2个广义力分别为：

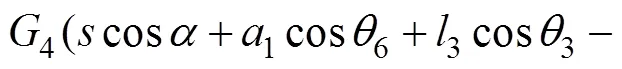
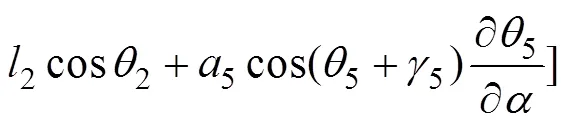
(12)

2.4 各液压油缸驱动力解析解的推导

将式(6)代入拉格朗日方程可得：

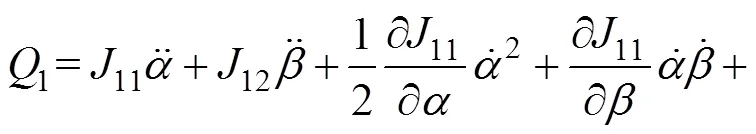
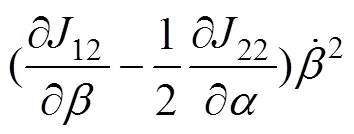
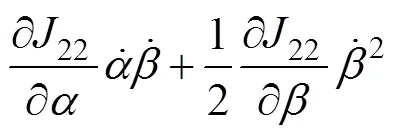
如前所述，调平机构的自动液压油缸和从动液压油缸的无杆腔与无杆腔相连、有杆腔与有杆腔相连，形成2个封闭回路。假设无杆腔的油压为1，有杆腔的油压为2，当变幅油缸伸出带动臂架绕点逆时针方向旋转时，自动液压油缸的无杆腔受拉，因此，1=0。经推导可得自动液压油缸和从动液压油缸的驱动力之间存在如下关系：

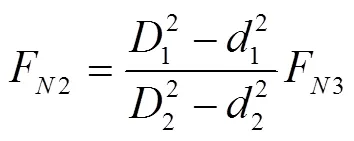
式中：1和1分别为自动液压油缸的缸筒内径和活塞杆直径；2和2分别为从动液压油缸的缸筒内径和活塞杆直径。

结合式(11)~(15)，可分别求得调平机构的3个液压油缸的驱动力分别为：

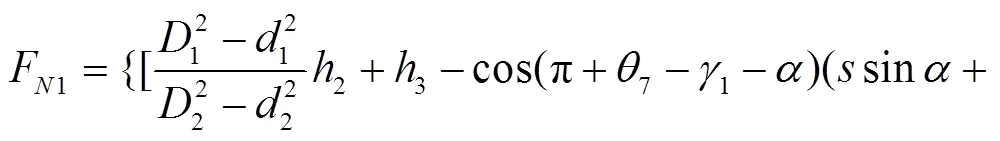
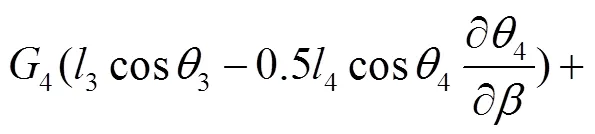
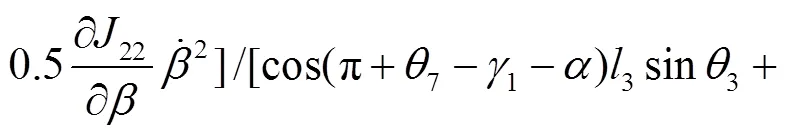
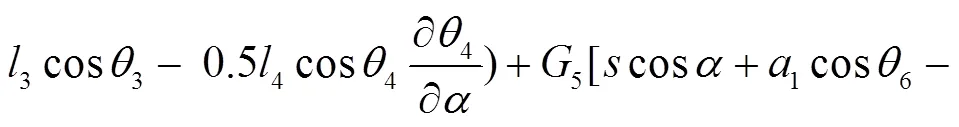
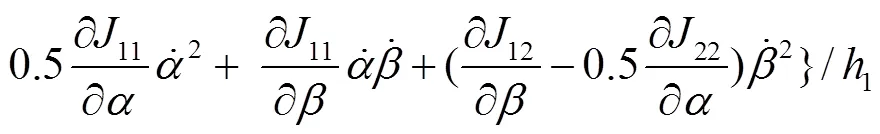
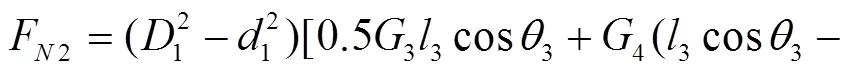
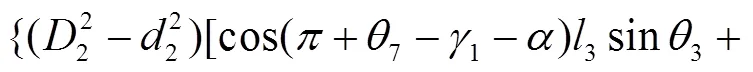
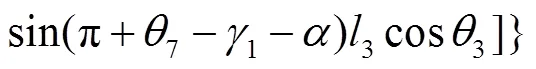
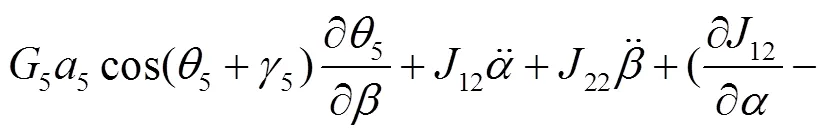
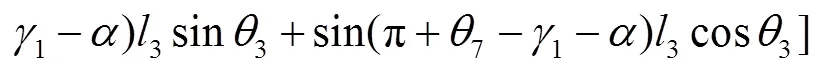
式(16)~(18)分别为调平结构的3个液压油缸驱动力的动力学解析解，直观揭示了哪些参数与各液压油缸驱动力相关联，可用于动力学分析以及机构进一步优化设计。若在工程设计中进行简化处理，则只需令式(16)~(18)中的各角速度和角加速度为0，即可获得3个液压油缸驱动力的静力学解析解。

3 工程实例仿真分析

图6表明：调平机构的负载越大，所需的各液压油缸驱动力越大；在3个液压油缸驱动力中，自动液压油缸和从动液压油缸的驱动力对负载变化更敏感：当负载由空载增大至1 500 kg时，变幅液压油缸驱动力只增大至原来的1.7倍左右，而自动液压油缸和从动液压油缸的驱动力均增大至原来的3.2倍。

由图6还可知：在同样的负载作用下，随着臂架转角不断增大，3个液压油缸的驱动力均不断减小，且这3个油缸驱动力中变幅液压油缸的驱动力始终最大；随着臂架转角不断增大，这种差距逐渐缩小。自动液压油缸和从动液压油缸这两者的驱动力中，自动液压油缸的驱动力更小，由式(15)可知这是由2个液压油缸的缸筒内径和活塞杆直径决定的。总体上，自动液压油缸驱动力和从动液压油缸驱动力与变幅液压油缸驱动力相比都低1个数量级，因此，在工业设计中，可根据实际安装空间选择这2个液压油缸的型号。

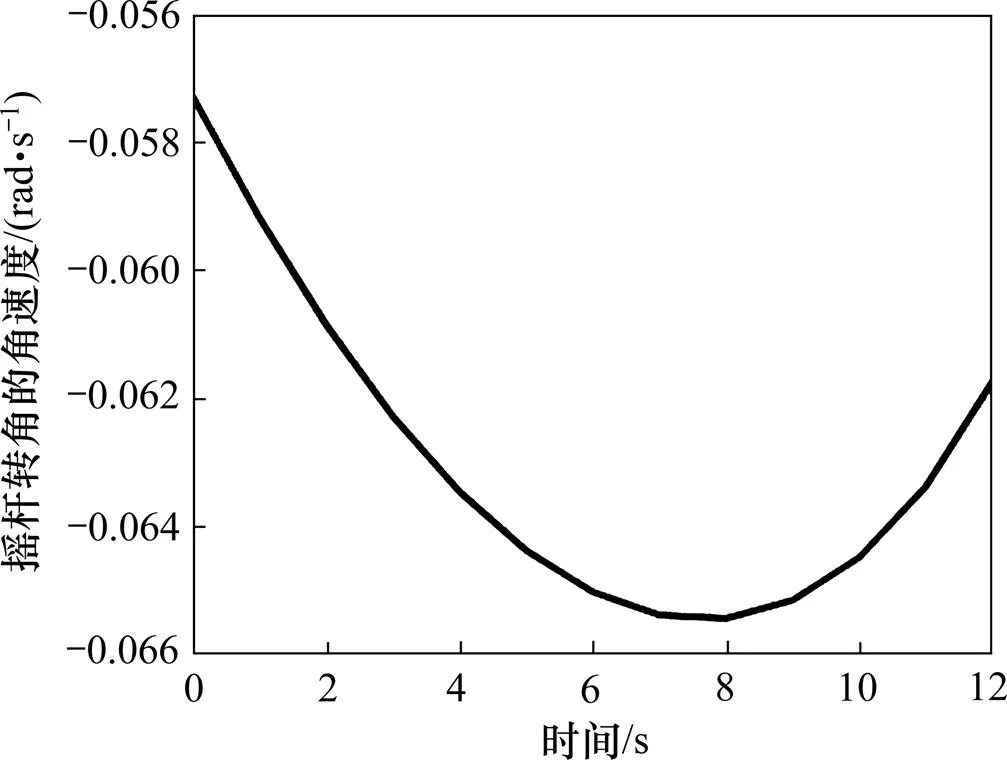
图4 摇杆转角的角速度

图5 摇杆转角的角加速度

1—1 500 kg负载时的变幅液压油缸驱动力曲线；2—空载时的变幅液压油缸驱动力曲线；3—1 500 kg负载时的从动液压油缸驱动力曲线；4—1 500 kg负载时的自动液压油缸驱动力曲线；5—空载时的从动液压油缸驱动力曲线；6—空载时的自动液压油缸驱动力曲线。

图6 3个液压油缸的驱动力曲线

Fig. 6 Driving force curve of three hydraulic cylinders

此外，还对各液压油缸驱动力的静力学解析解和动力学解析解进行仿真对比分析，仿真结果表明：当臂架匀速转动举升工作平台时，惯性力和惯性力矩对各液压油缸驱动力的影响较小，各液压油缸的驱动力主要用于克服机构自身重力和负载。

4 试验验证

以山河智能装备集团研制的SWTH3514型伸缩臂叉装车为试验对象，调平机构的负载为1 500 kg。2个压力传感器分别安装在多路阀至变幅液压油缸有杆腔和无杆腔的出口处，将压力传感器的另一端连接至手持式液压测试仪，即可分别测得举升过程中变幅液压油缸的有杆腔和无杆腔的压力变化情况。已知变幅液压油缸缸筒内径和活塞杆直径，即可由试验测得的有杆腔和无杆腔的压力曲线获得变幅液压油缸的驱动力曲线。仿真和试验所得变幅液压油缸的驱动力曲线如图7所示。对比图7中的变幅液压油缸驱动力仿真结果和试验结果可知：两者具有相同的变化趋势，且吻合度较高，由此可判断所采用的数学模型及仿真模型是正确的，说明该动力学模型能够较真实地反映调平机构的动力学特性。

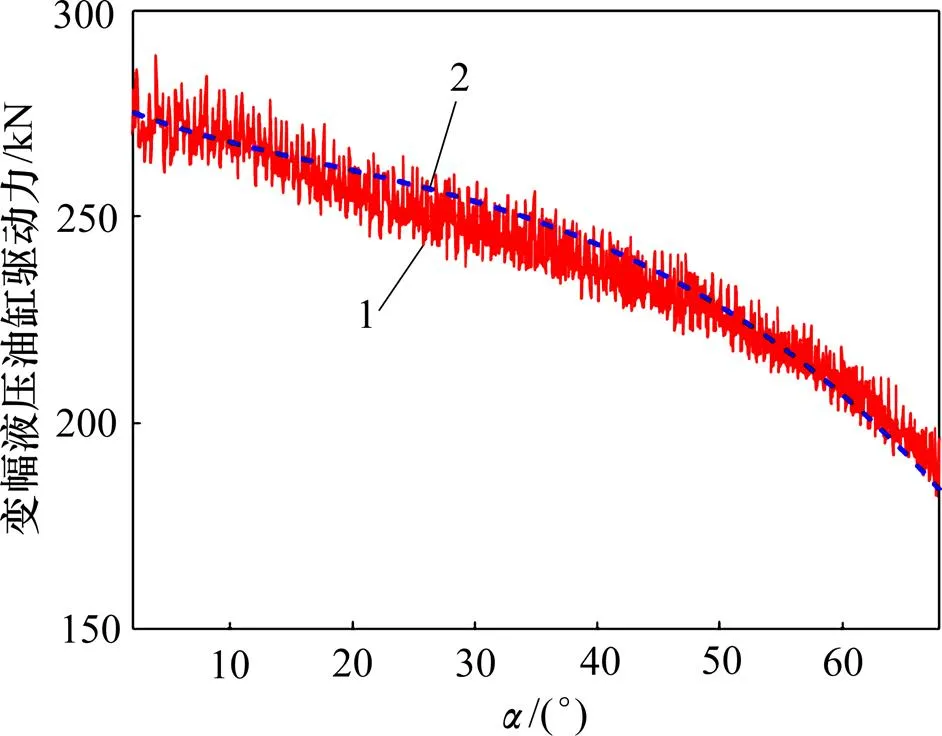
1—试验结果；2—仿真结果。

5 结论

1) 分别推导了调平结构3个液压油缸驱动力的动力学解析解，直观揭示了与各液压油缸驱动力直接关联的参数，可用于工程设计计算和分析，也可用于进一步机构优化设计。

2) 通过3个液压油缸驱动力的动力学解析解可以获得对应的静力学解析解，适用于工程设计中的简化处理情况。

3) 自动液压油缸驱动力、从动液压油缸驱动力和变幅液压油缸驱动力三者中，前两者对负载变化更 敏感。

4) 自动液压油缸驱动力和从动液压油缸驱动力的相对大小由两者的缸筒内径和活塞杆直径决定。在工程设计中，可主要根据安装空间选择自动液压油缸和从动液压油缸的型号。

[1] 张磊庆. 国内高空作业平台及市场发展分析[J]. 建筑机械化, 2017, 38(8): 11−13. ZHANG Leiqing. Analysis on the domestic aerial work platform and market development[J]. Construction Mechanization, 2017, 38(8): 11−13.

[2] 闫洪峰, 王志, 邹卓然, 等. 基于 ADAMS 的伸缩臂叉装车属具调平机构设计[J]. 建筑机械, 2016(9): 62−65. YAN Hongfeng, WANG Zhi, ZOU Zhuoran, et al. Leveling mechanism design for attachment of telescopic handler based on ADAMS[J]. Construction Machinery, 2016(9): 62−65.

[3] DERLUKIEWICZ D, PRZYBYLEK G. Chosen aspects of FEM strength analysis of telescopic jib mounted on mobile platform[J]. Automation in Construction, 2008, 17(3): 278−283.

[4] 何清华, 朱俊霖, 王石林, 等. 伸缩臂叉装车变幅机构的铰点位置优化[J]. 华中科技大学学报(自然科学版), 2011, 39(11): 423−429. HE Qinghua, ZHU Junlin, WANG Shilin, et al. The optimization of the hinge point position of leveling mechanism for the telescopic handler[J]. Journal of Huazhong University of Science and Technology(Nature Science), 2011, 39(11): 423−429.

[5] 王石林. 伸缩臂叉装车工作装置动力学特性研究及优化设计[D]. 长沙: 中南大学机电工程学院, 2011: 23−28. WANG Shilin. Dynamical characteristic analysis and optimal design of the work device of the telescopic handler[D]. Changsha: Central South University. School of Mechanical and Electrical Engineering, 2011: 23−28.

[6] 李联勇, 辛宏彦, 白日. 高空作业平台调平机构力学分析[J]. 建筑机械化, 2010, 31(8): 44−46. LI Lianyong, XIN Hongyan, BAI Ri. Mechanics analysis of leveling mechanism of aerial work platform[J]. Construction Mechanization, 2010, 31(8): 44−46.

[7] 闫洪峰, 王伟平, 王志, 等. 基于ADAMS的伸缩臂叉装车工作装置运动学与动力学仿真[J]. 起重运输机械, 2013(9): 57−62. YAN Hongfeng, WANG Weiping, WANG Zhi, et al. ADAMS based Kinematics and dynamics simulation of telescopic handler working device[J]. Hoisting and Conveying Machinery, 2013(9): 57−62.

[8] 张鹏. 伸缩臂式高空作业平台调平机构仿真与优化[D]. 南京: 南京林业大学机械电子工程学院, 2010: 23−29. ZHANG Peng. Simulation and optimization of telescopic boom aerial work platform leveling mechanism[D]. Nanjing: Nanjing Forestry University. Institute of Mechanical and Electric Engineering, 2010: 23−29.

[9] 赵伟, 李洪彪. 基于ADAMS的飞机除冰车臂架调平机构仿真分析[J]. 工程机械, 2010, 41(2): 20−23. ZHAO Wei, LI Hongbiao. ADAMS based simulation analysis of the leveling mechanism for boom frame of airplane ice removing vehicle[J]. Construction Machinery, 2010, 41(2): 20−23.

[10] GUPTA A, RATTAN S S, MUKHERJEE S. Dynamic analysis of compliant−based slider crank mechanism using the environments like ANSYS[J]. International Journal of Mechanisms and Robotic Systems, 2016, 3(4): 317−332.

[11] 程靖, 陈力. 闭链双臂空间机器人动力学建模及力矩受限情况下载荷运动自适应控制[J]. 工程力学, 2017, 34(2): 235−241. CHENG Jing, CHEN Li. Dynamics for dual-arm floating space robot with closed chain and adaptive control for object motion with limited torque[J]. Engineering Mechanics, 2017, 34(2): 235−241.

[12] 于红英, 唐德威, 王建宇. 平面五杆机构运动学和动力学特性分析[J]. 哈尔滨工业大学学报, 2007, 39(6): 940−943. YU Hongying, TANG Dewei, WANG Jianyu. Analysis of the kinematic and dynamic characteristics of a planar five-bar mechanism[J]. Journal of Harbin Institute of Technology, 2007, 39(6): 940−943.

[13] 刘乃军, 牛军川. 2-PRC-FP(C)并联机构减振平台及其动力学特性[J]. 中南大学学报(自然科学版), 2017, 48(4): 925−935. LIU Naijun, NIU Junchuan. 2-PRC-PR(C) parallel mechanism platform for vibration isolation and its dynamics[J]. Journal of Central South University(Science and Technology), 2017, 48(4): 925−935.

[14] 熊小琴，何广平. 仿袋鼠单腿跳跃机器人动力学建模与仿真[J]. 北方工业大学学报, 2009, 21(3): 36−41. XIONG Xiaoqin, HE Guangping. Dynamics Modelling and numerical simulation of one-leg hopping kangaroo robot[J]. Journal of North China University of Technology, 2009, 21(3): 36−41.

[15] 丁华锋, 刘征, 刘帅, 等. 一种新型正铲液压挖掘装置的运动学和动力学分析[J]. 机械工程学报, 2015, 51(1): 60−68. DING Huafeng, LIU Zheng, LIU Shuai, et al. Kinematics and dynamics analysis of an innovative face-shovel hydraulic excavator in mining[J]. Journal of Mechanical Engineering, 2015, 51(1): 60−68.

[16] 康辉梅, 许怡赦, 金耀. 伸缩臂叉装车工作装置运动学分析[J]. 机械设计, 2015, 32(5): 39−42. KANG Huimei, XU Yishe, JIN Yao. Kinematic analysis of working device in telehandler[J]. Journal of Machine Design, 2015, 32(5): 39−42.

Dynamic characteristic of hydraulic leveling mechanism with a hybrid kinematic chain

KANG Huimei1, ZHU Jianxin2, WANG Shilin2

(1. School of Engineering and Design, Hunan Normal University, Changsha 410081, China;2. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)

To research the dynamic performance of the hydraulic leveling mechanism with a hybrid kinematic chain, such as lifting capacity and leveling ability, a dynamic mathematical model was established based on the Lagrange approach after rewriting the differential expression and the variational expression for the Euler angle of the working platform in the lifting process. The process were as follows: the complex vector method was used to establish the mass center velocity equations of the rigid bodies; the kinetic energy equation of the leveling mechanism was derived; the generalized force equations of the leveling mechanism were derived based on the principle of virtual work, and the dynamic analytical solutions of the driving forces of each hydraulic cylinder were deduced. The MATLAB software was used to simulate the mathematical model, and the driving forces of three hydraulic cylinders under different loads were analyzed. The simulation results were tested and verified by experiments. The results show that both loads of automatic hydraulic cylinder and driven hydraulic cylinder are more sensitive than the load of luffing hydraulic cylinder when different loads are applied in the working platform. The relative size of the load of automatic hydraulic cylinder and that of the driven hydraulic cylinder is determined by the diameters of the non-rod chamber and the piston rod. The analytic solutions of the loads of hydraulic cylinders can be used both in engineering design calculation and mechanism optimization design.

leveling mechanism; dynamic analysis; Lagrange approach; hybrid kinematic chain; MATLAB software

TH112

A

1672−7207(2019)03−0557−07

10.11817/j.issn.1672-7207.2019.03.008

2018−08−10；

2018−10−12

湖南省教育厅优秀青年科研基金资助项目(15B136)；国家自然科学基金资助项目(51775185) (Project(15B136) supported by the Scientific Research Fund of Education Department of Hunan Province; Project(51775185) supported by the National Natural Science Foundation of China)

康辉梅，博士，副教授，从事机构动力学分析及优化设计研究；E-mail: plum_007@sina.com.cn

(编辑 陈灿华)