一种新的基于椭圆曲线码的子域子码的McEliece密码系统
2019-04-15赵鸿伯钱路雁金玲飞
赵鸿伯 钱路雁 金玲飞,2
1(复旦大学计算机科学技术学院 上海 201203) 2(东南大学移动通信国家重点实验室 江苏 南京 210096)
0 引 言
1994年,Shor提出了能够在多项式时间复杂度内解决整数分解问题和离散对数问题的量子算法[1],这意味着在可实用的量子计算机出现的背景下,现今被广泛使用的RSA公钥密码系统及椭圆曲线公钥密码系统将不再安全。因此,密码学界开始研究能够抵抗量子计算机攻击的后量子密码系统,基于编码理论的密码系统便是后量子密码系统中的一类。
第一个基于编码理论的密码系统是由McEliece在1978年提出的基于二元Goppa码的McEliece公钥密码系统[2]。这一密码系统与现今使用的公钥密码系统相比拥有更快的加解密速度。到目前为止,尚没有有效的针对基于Goppa码的密码系统的攻击方法。
在后续的研究中,学者们尝试使用其他的纠错码来构造新的McEliece密码系统。2005年,Gaborit提出使用QC-BCH码来构造新的McEliece密码系统[3]。2007年,Baldi等[4]提出了基于QC-LDPC码的McEliece密码方案。2009年,Berger等[5]介绍了使用QC-alternant码构造的McEliece密码方案。2013年,Misoczki等[6]构造了基于QC-MDPC码的McEliece密码系统。2018年,NIST举行的后量子密码学标准竞赛上,多个基于编码理论的密码系统进入第一轮竞争,Aragon等[7]提出了基于QC-MDPC码的BIKE密码系统,Melchor等[8]学者提出的基于QC码的HQC密码系统等。
上述的部分密码方案被证明存在弱点。2010年,Otmani等[9]提出了针对Gaborit和Baldi提出的基于QC-BCH码和QC-LDPC码的McEliece密码系统的攻击方法。同一年,Faugère等[10]提出了针对Berger等人设计的基于QC-alternant码的McEliece密码方案的攻击方法。2016年,Guo等[11]提出了针对Misoczki等人构造的基于QC-MDPC码的McEliece密码方案的攻击方法。
除了上述方案外,1996年,Janwa和Moreno提出代数几何码及其子码可以作为构造McEliece密码系统的一种选择[12]。虽然基于代数几何码及其子码的McEliece密码系统已经被证明不安全[13]。但目前尚没有针对基于代数几何码的子域子码的McEliece密码系统的有效的攻击方法,代数几何码的子域子码仍然可以作为构造McEliece公钥密码方案的一个选择。
本文的主要贡献在于构造了一个新的基于椭圆曲线码的子域子码的McEliece公钥密码系统。
1 预备知识
1.1 线性码基础知识
1.2 代数几何码
Goppa于1977年发现了编码理论与代数几何之间的理论联系,并在1981年提出了代数几何码的构造方法[14]。

(1)
这个赋值映射的像就是一个从曲线X上构造的代数几何码,记为CL(X,P,E)。CL(X,P,E)的码长n等于有理点的个数,即n=|P|。CL(X,P,E)维数k等于L(E)的维数,即k=dim(L(E))。CL(X,P,E)的码距d由曲线X的亏格g决定,满足条件n-k-g+1≤d≤n-k+1[16]。
1989年,Justesen等学者提出了构造基于有限域上的光滑不可约仿射曲线的代数几何码的简易方法[17]。根据单项式基底F(x)和曲线的一个有理点集P,可以构造出曲线上的代数几何码的生成矩阵:
(2)
1.3 McEliece密码系统
初始的McEliece密码系统是基于Goppa码构建的。该密码系统由密钥生成、加密算法和解密算法三个部分构成。
1.3.1 密钥生成
1) 在有限域F2m上随机选取一个度数为t的不可约多项式。根据这一多项式构造一个参数[n,k,d]Goppa码的生成矩阵G,其中n=2m,d=2t+1。
2) 随机选择一个k×k的可逆矩阵S和一个n×n的置换矩阵P。
3) 计算公钥Gpub=SGP。
4) 将集合(S,φ,P)作为私钥保存,其中φ代表二元Goppa码的快速译码算法。
1.3.2 加密算法
令m代表一个长度为k的消息向量。加密算法的执行过程如下:
1) 随机生成一个长度为n的错误向量e,满足wt(e)≤t。
2) 计算密文c=mGpub+e。
1.3.3 解密算法
对于获得的密文c,解密算法的执行过程如下:
1) 消除置换矩阵的影响:计算x=cP-1=mSG+eP-1。
2) 使用译码算法φ清除错误向量:u=φ(x)。
3) 计算消息向量:m=uS-1。
2 基于椭圆曲线码的子域子码的McEliece公钥密码系统
2.1 基本思路
与其他代数几何码的子域子码相比,椭圆曲线码的子域子码拥有更长的码距。同时,2.4节中介绍了针对椭圆曲线码的子域子码的快速译码算法。这使得椭圆曲线码的子域子码成为构造McEliece公钥密码系统的一个选择。
本节将介绍基于椭圆曲线码的子域子码的McEliece公钥密码系统。与初始的McEliece公钥密码系统类似,基于椭圆曲线码的子域子码的McEliece公钥密码系统也由密钥生成、加密算法和解密算法三个部分组成。
2.2 密钥生成
2.2.1 构造椭圆曲线码
2) 随机选择X上的n个有理点P(α,β)构成有理点集P={P1,P2,…,Pn}。

4) 将F(x,y)按照V(f1)≤V(f2)≤…≤V(fn-t-1)顺序排列,其中V(f)=2i+3j。
5) 使用F(x,y)的前k个单项式Fk(x,y)和有理点集P构造椭圆曲线码的生成矩阵Ge。构造的椭圆曲线码的参数为[n,k,d],其中d=n-k。
2.2.2 构造椭圆曲线码的子域子码
1) 根据Ge计算椭圆曲线码的校验矩阵He。
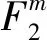
3) 椭圆曲线码的子域子码的生成矩阵G是H2的零空间的一个基底。构造的子域子码的参数为[N,K,D],其中N=n,K≥mk-(m-1)n,D≥d。
2.2.3 生成密钥
1) 随机挑选一个F2上的k×k可逆矩阵S,一个n×n转置矩阵P。
2) 计算公钥Gpub=SGP。
3) 将有理点集P,可逆矩阵S和转置矩阵P作为私钥保存。
2.3 加密算法
对一个消息向量m的加密过程如下:
1) 随机生成一个长度为n的错误向量e且wt(e)≤t。
2) 生成密文r=mGpub+e。
2.4 解密算法
2.4.1 椭圆曲线码的子域子码的快速译码算法

1) 构造两个多项式A(x,y)、B(x,y):
A(x,y)=a1f1+a2f2+…+an-t-1fn-t-1
(3)
B(x,y)=b1f1+b2f2+…+bn-t-k-1fn-t-k-1
(4)
其中,ai,bi∈q,fi∈F(x,y)。
2) 构造方程组A(Pi)+B(Pi)f(Pi)=0,找到A、B的一个非零解:
(5)
4) 纠错后的码字为{d(P1),d(P2),…,d(PPn)}。
2.4.2 快速译码算法证明
本节将证明椭圆曲线码的子域子码的快速译码算法的正确性。
1) 证明多项式A(x,y)、B(x,y)的存在性:将ai、bj看作是未知数,则式(5)是一个包含n个齐次线性方程的齐次方程组。其中未知数的个数为2(n-t-1)-k 2) 证明纠错后的码字等于{d(P1),d(P2),…,d(Pn)}。不妨设收到的码字mGpub等于(f(P1),f(P2),…,f(Pn)),其中V(f)≤k。由1)知,至少有n-t个有理点Pi使得A(Pi)+B(Pi)f(Pi)=0。又由V(A+Bf) 2.4.3 解密算法 根据上文介绍的椭圆曲线码的子域子码的快速译码算法,对收到的密文r=mSGP+e={r1,r2,…,rn},解密算法过程如下: 1) 消除置换矩阵P的影响:r′=rP-1=mSG+e′。 2) 清除错误位:m′=Φ(r′)=mS。 3) 恢复消息向量:m=m′S-1。 目前,针对McEliece密码系统主要存在两类攻击方法。第一类攻击尝试从密文中恢复明文信息的信息恢复攻击,信息集译码攻击算法是这一类攻击算法的代表,3.2节中讨论了信息集译码攻击算法对提出的密码方案的安全性的影响。第二类是根据选取的编码的性质,试图从公钥中恢复私钥的密钥恢复攻击。目前,尚没有直接针对基于椭圆曲线码的子域子码的McEliece密码系统的密钥恢复攻击方法。由于椭圆曲线码是构建在亏格为1的代数曲线上的代数几何码,因此3.4节中讨论了针对基于代数几何码的McEliece密码系统的密钥恢复攻击对提出的密码系统的影响。最终证明,在现有的攻击方法下,本文中提出的密码系统是安全的。 穷搜攻击的基本思路是根据公钥矩阵的信息,通过遍历搜索所有可能的k×k可逆矩阵,n×n置换矩阵以及使用的有理点集的方法,恢复出私钥(S,P,P)。在2上,k×k可逆矩阵的个数为置换矩阵的个数为在q上,不同构的椭圆曲线的个数约为|X|≈2q[19]。椭圆曲线上的有理点的数量区间为椭圆曲线上基数为n的有理点集|P|的数量区间为 基于上述分析,攻击者成功实施穷搜攻击的可能性为1/|S||P||P||X|。当n、k取较大值时,设计的密码系统能够有效抵御穷搜攻击。 1962年,Prange针对一般线性码的译码问题提出了信息集译码算法[20]。 定义1令G代表一个[n,k]线性码C的生成矩阵,I代表{1,2,…,n}的一个基数为k的子集。选择G中以I为索引的列构成一个k×k矩阵GI。若GI可逆,则称I为G的一个信息集。 下面是信息集译码算法的一个简单例子。 令I代表q上的一个线性码C的生成矩阵G的一个信息集,y代表上的一个向量,c代表C的一个码字,且d(y,c)=w,w≠0。令yI和cI代表按I索引的y和c的子集。若yI=cI,则可以计算码字 表1 信息集译码攻击算法的时间复杂度 1997年,Berson和Thomas证明McEliece公钥密码系统在消息重传场景下是不安全的[26]。 令m代表一个明文向量。假设存在两个由m生成的密文c1=mGpub+e1和c2=mGpub+e2其中e1≠e2。由McEliece密钥方案的初始定义可知c1-c2=e1-e2。根据这一关系,攻击者可以快速的找到一个信息集I使得cI=mI,从而恢复出明文m。 和初始的McEliece密钥方案相同,基于椭圆曲线码的子域子码的McEliece密钥方案在消息重传场景下也是不安全的。 为了使McEliece密码系统达到CCA-2安全级别。有学者提出了可用于基于编码理论的密码系统的具有CCA-2安全级别的加密方案[27-28]。 目前,尚没有针对基于代数几何码的子域子码的McEliece密码系统的攻击方法。由于选择的编码是代数几何码的一类子码,本节将分析针对基于代数几何码的McEliece密钥系统的攻击方法对提出的密钥系统的安全性能的影响。 3.4.1 Faure的攻击算法 2007年,Faure和Minder提出了针对基于椭圆曲线码的McEliece密钥系统的攻击算法[29]。这一算法的基本思路是,根据椭圆曲线上所有有理点构成的阿贝尔群,攻击者能够找到一条与选择的曲线同构的椭圆曲线,并最终根据两条曲线间的映射来恢复所选用的椭圆曲线。 为了从公开信息中构造所选用的椭圆曲线的所有有理点构成的阿贝尔群,攻击者需要找到所选用的椭圆曲线码的一个具有最小汉明重量的码字。 定义2对于一个[n,k,d]椭圆曲线码,其码字的最小汉明重量等于它的码距d=n-k。 椭圆曲线码的子域子码的码距大于等于其原码的码距。在实际构造中,当椭圆曲线码所在的有限域大于26时,总能构造出码距大于原码码距的子域子码。比如,参数为[64,54,10]的椭圆曲线码的子域子码的参数为[64,10,16],参数为[128,113,15]的椭圆曲线码的子域子码的参数为[128,23,36]。 无法从子域子码中获得原码的一个具有最小汉明重量的码字使得Faure的攻击算法对提出的密码方案无效。 3.4.2 Couvreur的攻击算法 2017年,Couvreur等人提出了针对基于代数几何码及其子码的McEliece系统的攻击算法。但Couvreur等在论文中阐明,这一攻击算法并不适用于基于代数几何码的子域子码的McEliece密码系统[13]。 与最初的McEliece密码方案相同。提出的基于椭圆曲线码的子域子码的McEliece密码系统的公钥是一个大小为n×k比特的矩阵。合适的具有CCA-2安全级别的加密方案能够在保持安全性能的同时,将密钥方案的公钥转变为一个大小为(n-k)×k比特的标准形式矩阵[30]。 本文的主要贡献在于构造了一个新的基于椭圆曲线码的子域子码的McEliece公钥密码系统。并使用针对McEliece公钥密码系统的攻击算法及针对基于代数几何码的McEliece密码系统的攻击算法对提出系统的安全性能进行分析。分析证明,在现有的攻击下,本文提出的基于椭圆曲线码的子域子码的公钥密码系统是安全的。 未来该方案可作为基于编码理论的密码系统的一个备选方案,在数字签名、零知识证明等方面展开进一步的研究。3 安全性能分析
3.1 穷搜攻击
3.2 信息集译码攻击
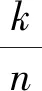

3.3 消息重传攻击
3.4 针对基于代数几何码的McEliece公钥系统的密钥恢复攻击
3.5 公钥体积及推荐参数
4 结 语
