基于深度神经网络和局部描述符的大规模蛋白质互作预测方法

桂元苗 王儒敬 王 雪,3 魏圆圆

1(中国科学院合肥物质科学研究院智能机械研究所 安徽 合肥 230031) 2(中国科学技术大学信息技术学院 安徽 合肥 230026) 3(中国科学院合肥物质科学研究院技术生物与农业工程研究所 安徽 合肥 230031)

0 引 言

蛋白质相互作用PPI是生物体中众多生命活动过程的重要组成部分，在许多细胞生物学过程中起着重要的作用。新陈代谢、信号转导、细胞周期调控、新陈代谢、细胞凋亡及免疫应答等一系列生命活动都是通过蛋白质相互作用实现的。蛋白质互作预测是研究蛋白质互作的重要途径。近几年涌现了诸多预测蛋白质相互作用的高通量实验方法，例如：酵母双杂交方法[1]、质谱蛋白质复合物鉴别[2]、质谱分析[3]以及蛋白质芯片方法[4]等。然而，这些使用化学实验的方法，需要耗费大量的人力、财力和时间，难以应用于大规模的蛋白互作预测。机器学习的出现，使大规模的蛋白互作预测成为可能。到目前为止，已经出现的大量机器学习模型，包括支持向量SVM[5]、神经网络NN(Neural Networks)[6]、朴素贝叶斯[7]、K-最近邻[8]等已经被用来预测PPI。 尽管上述PPI预测方法很流行，但仍然存在一定的局限性，一般的机器学习模型无法很好地处理蛋白序列噪声输入中的隐性关联[9-11]。深度神经网络的出现，为这类问题提供了强有力的解决方案。

深度神经网络(DNN)是机器学习中最活跃的领域之一，可自动从数据中提取高层抽象信息，用于复杂预测任务，如语音和图像识别[12]、自然语言理解[13]、决策制定[14]以及最近的计算生物学[15-17]。Leung等[16]利用深度神经网络和rna-seq数据，建立了一个预测个体组织和组织间剪接模式差异的模型；Zhou等[17]使用深度神经网络开发了深度学习框架(DeepSEA http://deepsea.princeton.edu/)。该框架可以从染色质谱分析序列中学习调控序列代码，并且可以改进功能变体的优先级。与基于序列的其他机器学习方法相比，深度神经网络具有几个优点：(1) Bengio等[18]证明深度神经网络能够减少噪声对原始数据的影响，并学习真正隐藏的高层特征；(2) Alipanahi等[19]发现，深度神经网络可以使用各种实验数据和评估指标自动学习蛋白质的特定序列基序；(3) Krizhevsky等[20]人为地将噪声引入基于深度神经网络的方法来减少过度拟合，并且揭示深度神经网络可以增强模型泛化。最近，深度神经网络用于蛋白网络互作也取得了良好的结果[15,21]，Tian等[21]提出了一种称为DL-CPI(复合蛋白质相互作用预测的深度学习的缩写)的方法。该方法使用深度神经网络通过分层提取来学习复合蛋白对的有用特征，从而在平衡数据集和不平衡数据集上取得了比现有方法更好的预测性能，有效地提高复合蛋白互作的预测性能。Du等[15]使用深度神经网络基于氨基酸序列来研究蛋白互作预测，并分别获得了92.50%的准确率和90.50%的召回率。尽管深度神经网络算法在蛋白质互作预测中取得了成功的结果，但基于深度神经网络和局部描述符的蛋白互作预测的研究很少见。

本文首先采用局部描述符将蛋白质序列编码成固定长度的向量，并随机分成训练集和测试集；然后将训练集输入深度神经网络，调整并优化网络结构和学习率、丢弃率等模型参数，训练蛋白互作预测模型DPPI；最后DPPI模型经过测试和验证用于蛋白质互作预测，并将预测的结果和前人的蛋白质互作预测方法进行比较。

1 基础方法

1.1 局部描述符

深度学习等机器学习方法的输入均为某一维数空间中的向量。为使深度学习方法学习并预测蛋白互作关系成为可能，必然要求将长度不统一的蛋白序列编码成某一维数空间中的向量。为了将蛋白质序列编码成维数相同的空间向量，Yang等[22]首次将局部描述符LD(Local Descriptor)应用于蛋白互作预测，在酒酿酵母数据集上达到86.15%的准确率。LD[23]是一种无需序列比对的方法，其效果在很大程度上取决于潜在的氨基酸分类。首先，依据氨基酸侧链的偶极性和体积将20种氨基酸分成7组(见表1)，并将蛋白序列中的所有氨基酸替换成对应的分组编码。例如，蛋白序列“MESSKKMDSPGALQTNP”转换成“363355363211

24342”。

表1 基于侧链的偶极子和体积的氨基酸分类

然后，依据氨基酸官能团在蛋白质初级序列中发生的变化计算Composition(C)、Transition(T)和Distribution(D)。其中：Composition为各组氨基酸在整条蛋白序列中所占的比例；Transition指一组氨基酸中的氨基酸残基和另外一组氨基酸中的氨基酸残基相邻的频率；Distribution指在一条蛋白质序列中每组氨基酸的氨基酸残基数目的第一个、25%、50%、75%和100%在整个蛋白质序列中所占位置的比例。所以一个氨基酸片段可以用63维的向量表示：7(计算C得到的)+21(计算T得到的(7×6)/2)+35(计算D得到的7×5)。

为了更好地从蛋白质的氨基酸片段中捕捉蛋白质相互作用信息，本实验将每条蛋白质序列划分为10个局部区域(A-J)，见图1。区域(A-D)是把一条蛋白质序列分成四个相等的区域；区域(E-F)是把一条蛋白质序列分成二个相等的区域；区域G表示位于蛋白质序列中间的50%氨基酸片段；区域H表示整条蛋白质序列的前75%的氨基酸片段；区域I表示整条蛋白质序列的后75%的氨基酸片段；区域J表示整条蛋白质序列的中间75%的氨基酸片段。一条蛋白质序列的所有局部区域氨基酸片段的编码，串联在一起就形成了一条蛋白质序列的编码，得到630维向量。因此，本文构造了一个1 260维向量来表示每个蛋白质对，并将其作为DPPI模型的输入向量。

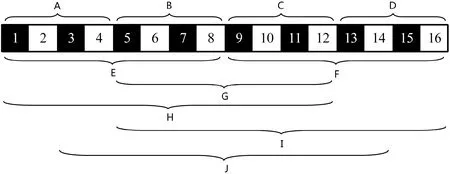
图1 一条蛋白质划分为10个区域的划分方法示意图

1.2 深度神经网络

DNN是指一组模仿人类大脑设计的，旨在识别模式的算法。DNN由输入层、一个或多个隐藏层以及输出层三部分组成，如图2所示。一般来说，第一层是输入层，最后一层是输出层，而中间的层都是隐藏层。相邻层之间全连接，即第i层的任意一个神经元与第i+1层的任意一个神经元相连。DNN类似于一般的人工神经网络，然而，隐藏层的数量和训练过程是不同的。Hinton等[24]利用预训练方法缓解了局部最优解问题，将隐含层推动到了7层后，DNN才有了真正意义上的“深度”。DNN在输入层接收数据，在各个节点中将输入数据与权重相结合以非线性方式转换这些数据，通过计算平均梯度并相应地调整权重和激活函数，最后在输出层计算最终输出。

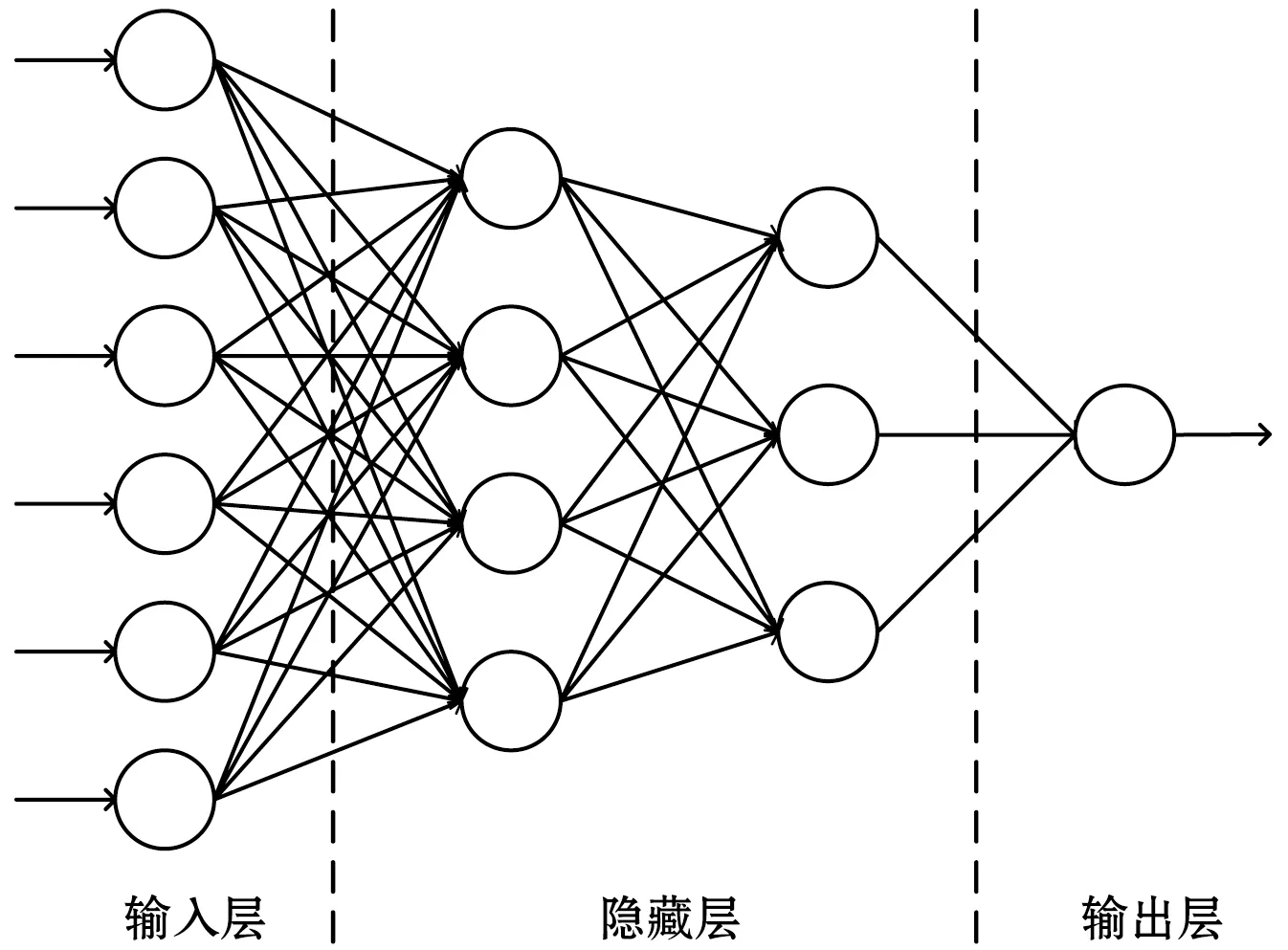
图2 深度神经网络结构

虽然DNN很复杂，但是从局部模型来说，还是和感知机一样，由一个线性关系加上一个非线性激活函数组成，用矩阵法表示，第l层的输出为：

al=δ(Zi)=δ(wlal-1+bl)

(1)

式中：l=1,2,…,N；al-1是第l层的输入数据；wl是第(l-1)层和第l层之间的连接权重矩阵；bl是第l层的偏置，δ表示第l层的激活函数。

目前，在DNN中，通常使用ReLU(Rectified linear unit)作为神经元的激活函数。如式(2)所示，ReLU具有单侧抑制特性，把所有的负值都变为0，而正值不变。这种单侧抑制会使神经网络中的神经元具有稀疏激活性，实现稀疏后的模型能够更好地挖掘相关特征和拟合训练数据。

δ(z)=max(0,z)

(2)

2 模型构建

2.1 数据集

本实验采用由Pan等[30]发布于http://www.csbio.sjtu.edu.cn/bioinf/LR_PPI/Data.htm的人类蛋白序列对数据集。该数据集包含36 630条阳性样本(有互作关系蛋白质序列对)和36 480条阴性样本(无互作关系蛋白质序列对)。其中：阳性样本取自人类蛋白质参考数据库(HPRD)2007版；阴性样本取自瑞士Swiss-Prot数据库57.3版。

实验侧重20种常见氨基酸组成的蛋白质序列，并且蛋白质序列编码方法要求蛋白质序列的长度不易太短。所以，实验过程中除去蛋白质序列长度少于50及含有B、J、O、U、X、Z的蛋白质序列对，得到36 591对阳性样本和36 324对阴性样本，分别从阳性样本和阴性样本随机选取30 000条蛋白质序列对组成训练集，剩下的12 915条蛋白质序列对作为测试集。

2.2 性能评价指标

实验采用准确率(Accuracy)、召回率(Recall)、损失率(Loss)和受试者工作特征曲线下面积AUC四个指标来评价模型性能。其中准确率和召回率计算公式如下：

(3)

(4)

式中：TP、TN、FP和FN分别代表真正、真负、假正和假负。AUC通过开源代码计算[37]。损失率是用来衡量模型的实际输出与期望输出的距离，损失函数越小，表示两个概率分布就越接近，模型的拟合性和鲁棒性就越好。损失率通过交叉熵函数计算公式如下：

(5)

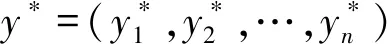
2.3 构建流程

DPPI模型是基于Tensorflow平台在Python环境下构建的，其构建流程如图3所示。主要包括以下几步：首先，使用LD分别对有关序列对和无关序列对的氨基酸序列进行编码，生成有关序列集和无关序列集；其次，使用随机选择的60 000条训练集数据对模型进行训练，生成DPPI模型；接着，使用剩下的12 915条测试集数据对DPPI模型进行测试；最后，对DPPI模型的预测性能进行评价，并根据评价结果调整参数，优化DPPI模型。

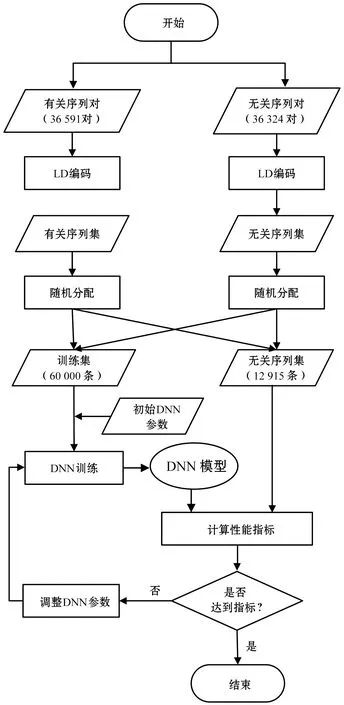
图3 DPPI模型构建流程图

2.4 参数调整

参数调整是模型训练过程中很重要的一步，是训练出健壮模型的关键要素之一。实验中，激活函数使用ReLU、优化器选择Adam、代价函数使用交叉熵。在优化器方面，目前已经开发了诸如RMSprop，Adagrad[27]和Adam[28]等优化方法，其中，Adam集合了RMSprop和Adagrad两个算法的优点，能够较好地处理噪声样本。交叉熵代价函数是用来衡量深度神经网络的预测值与实际值的一种方式，可以弥补sigmoid型函数的导数形式易发生饱和的缺陷，使训练更快收敛。

学习率决定了权值更新的速度，设置得太大易越过最优值，出现振荡现象；太小会使下降速度过慢，长时间无法收敛。因此，学习率直接决定着算法的性能表现。Bengio[29]认为一般常用的学习率有0.000 01、0.000 1、0.001、0.01、0.1，推荐使用的是0.01，同时Bengio也指出，学习率的选择要根据数据集的大小、特征提取方法等实际情况来确定。实验中，设定隐含层节点数为64、激活函数为ReLU、优化算法为Adam、批处理大小为128、迭代次数为300 000次，调整学习率的结果如表2所示。可以看出，学习率为0.001时的准确率最高、平均损失最小。

表2 DPPI模型学习率的调整

为了确定模型的宽度，设定激活函数为ReLU、优化算法为Adam、学习率为0.001、批处理大小为128、迭代次数为300 000次，调整模型宽度的结果如表3所示。可以看出，宽度为512时，模型的准确率最高，同时训练时间比宽度为256时增加了近一倍，而准确率、平均损失分别比宽度为256时仅仅提高了0.003 1、0.001 3，考虑到时间复杂度，本模型宽度选择256。

表3 DPPI模型宽度的调整

模型的宽度、激活函数、优化算法、学习率等确定之后，本文通过调整隐含层层数来确定模型的深度，调整深度的结果如表4所示。根据表4，可知网络深度为[256-128-64-32]时的准确率较高、平均损失较低，训练时间较短。

表4 DPPI模型深度的调整

丢弃率是DNN中防止过拟合、提高性能的一个很重要的参数。为了优化DPPI模型，本文通过调整丢弃率得到7个预测模型，各预测模型的最优结果如表5所示。从表5可知，丢弃率为0.025时准确率最高，达到96.81%，平均损失为15.72%；丢弃率为0.05时，准确率比丢弃率为0.025时的准确率降低了0.08%，同时平均损失降低了2.52%；不使用丢弃率时，准确率、AUC、Recall、平均损失分别为95.84%、97.44%、98.25%、45.38%。虽然不使用丢弃率时准确率和使用丢弃率时准确率差别不大，但不使用丢弃率的平均损失较高，所以不推荐使用。由此，DPPI-2和DPPI-3的性能较好，可以作为DPPI的最终预测模型。

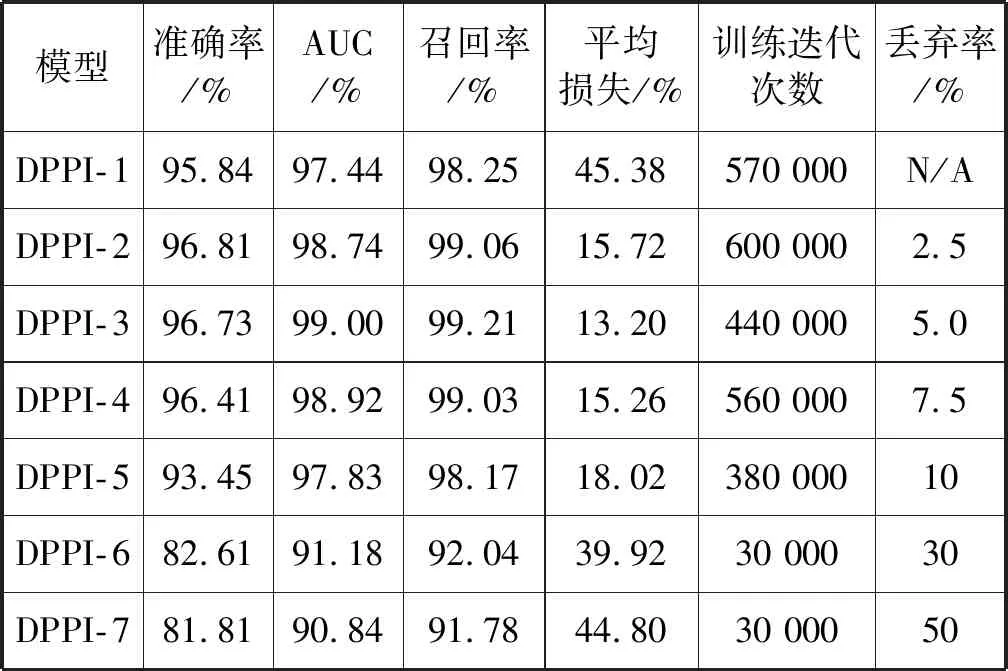
表5 DPPI模型的最优预测性能

经过超参数调整后，本文构建了一个包含4个隐藏层，各隐藏层节点数分别为256、128、64、32的DPPI模型。经过大量实验和调试，总结了本实验采用的参数，如表6所示。

表6 DPPI模型参数表

3 实 验

3.1 DPPI模型实验

参照表6的DPPI模型参数，根据使用和不使用丢弃率以及不同的丢弃率值，使用7个不同的DPPI模型进行计算。每个模型各迭代60万次，每1万次输出一个测试结果，各输出60个实验结果。所有实验结果的统计值见表7。可以看到，DPPI-2的准确率最高，DPPI-1和DPPI-3稍微次之。DPPI-3的AUC、召回率和平均损失这三个指标比其他6组表现更优异。特别地，DPPI-3的平均损失(15.34%)比DPPI-2的平均损失(16.99%)降低了1.65%。

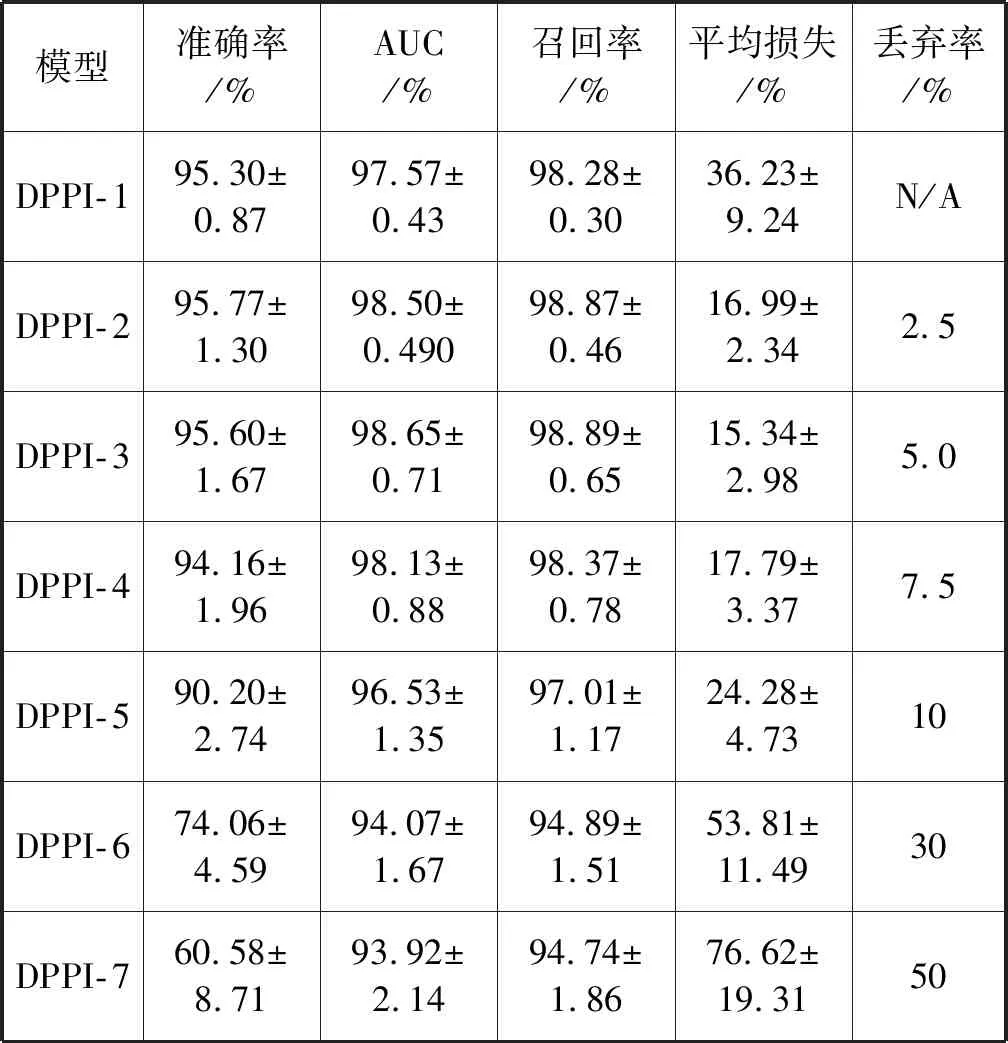
表7 DPPI模型预测性能平均值

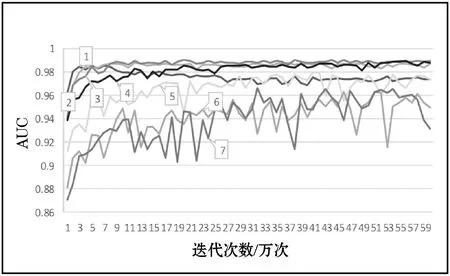
图4为7个DPPI预测模型不同评价指标的趋势图。其中：1代表DPPI-1预测指标趋势图；2代表DPPI-2预测指标趋势图；3代表DPPI-3预测指标趋势图；4代表DPPI-4预测指标趋势图；5代表DPPI-5预测指标趋势图；6代表DPPI-6预测指标趋势图；7代表DPPI-7预测指标趋势图。从图4(a)中可以看出，模型DPPI-6和DPPI-7随着迭代次数的增加，准确率呈下降趋势。DPPI-5的准确率虽然比DPPI-6和DPPI-3好，但DPPI-5准确率不稳定，振荡幅度稍大。从准确率来看，模型DPPI-1、DPPI-2、DPPI-3和DPPI-4准确率后期都比较稳定，DPPI-2的准确率最好。(b)是7个DPPI模型AUC趋势图，可以看出，模型DPPI-2、DPPI-3和DPPI-4后期结果比较平稳，虽然DPPI-1的结果开始较好，但后期较差。(c)是7个模型的召回率趋势图，DPPI-3的召回率性能较好，DPPI-5、DPPI-6和DPPI-7召回率较低，不平稳且振荡幅度较大。(d)是7个模型平均损失的趋势图，趋势图显示模型DPPI-2、DPPI-3和DPPI-4结果较好，但DPPI-2振荡幅度比DPPI-3稍大。

(a)

(b)

(c)

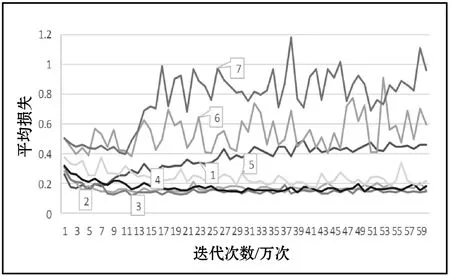
(d)图4 DPPI模型各个指标预测趋势图

综合表7和图4得到最终的预测模型DPPI-3，其准确率为95.6%，平均损失为15.34%。

3.2 方法比较

近几年，已经有许多研究者对人蛋白互作预测提出了不同的计算方法。这些人蛋白互作预测方法以及DPPI的性能比较结果见表8。可以看出，所列方法获得的精度均在83.90%和97.19%之间，同时，除了Sun[34]使用SAE+AC方法获得97.19%的准确率以外，DPPI模型获得了最好的准确率。和Sun的结果相比，虽然DPPI的准确率不算突出，但是Sun使用SAE+CT的准确率没有DPPI模型的准确率高。从表9可见，在酒酿酵母数据集上，DPPI模型和其他采用LD编码的方法比较，也取得最高准确率。

表8 不同方法的预测性能的比较

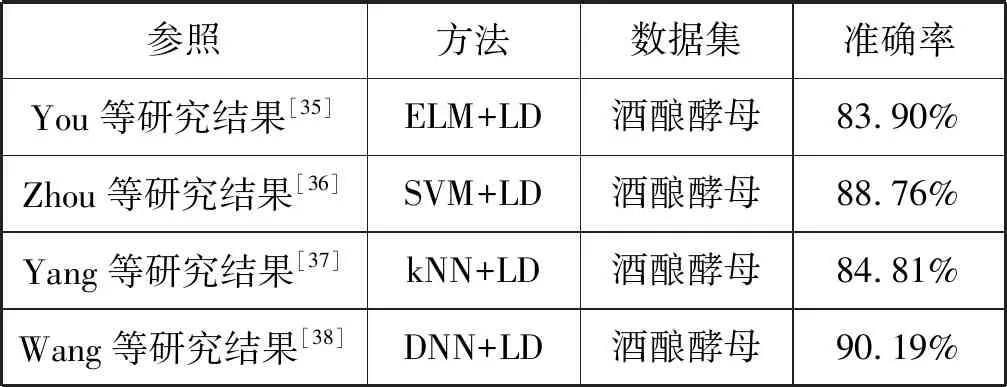
表9 不同算法采用LD编码方式结果比较

SAE+AC结果优于DPPI的原因可能在于特征提取方法的不同。AC编码是通过选择物理化学性质，解释了氨基酸与序列中相隔一定数量的氨基酸之间的相互作用，该方法考虑了最长序列30 bp的邻近效应[32]。LD为了更好地从蛋白质的氨基酸片段中捕捉蛋白质相互作用信息，将一条蛋白质序列划分为10个局部区域，这样分组，局部信息突出不明显，致使丢失某些关键信息[37]。LD的这种缺陷在以后的研究中，可以通过增加局部区域的划分等方法来减少特征信息的丢失。

虽然DPPI模型准确率和SAE+AC方法相比不算突出，但在蛋白互作预测方面也取得了良好的结果，且DNN去噪能力优于SAE，代码也比SAE简洁，LD编码简单、速度快。特别地，由表10可知，LD和AC编码72 915对人蛋白质的时间可见在相同软硬件计算环境下LD编码速度比AC编码速度快3.5倍以上。通过上面的比较可知，本文的DPPI模型与其他方法相比可以显著提高大规模蛋白互作预测性能。

表10 AC和LD编码时间的比较

4 结 语

深度学习算法已经涉足许多领域，但是在蛋白互作的研究中还没有被广泛的应用。因此，本文采用深度神经网络DNN和LD蛋白质序列编码方法相结合的方法构建了蛋白互作预测模型DPPI。DPPI模型获得准确率96.73%、AUC 99.00%、召回率99.21%和平均损失13.2%的最优性能，以及95.60%准确率、98.65%AUC、98.89%召回率和15.34%平均损失的平均性能。和其他研究者提出的人蛋白互作预测方法比较，DPPI模型的准确率优于Shen、You、Guo、Du、Pan等结果，但DPPI的结果没有Sun采用的SAE+AC方法预测结果性能好。LD的这种缺陷在以后的研究中，可以通过增加局部区域等方法来减少特征信息的丢失。

本文首次采用DNN结合LD对人蛋白互作数据集构建的，用于蛋白互作预测的模型DPPI。该模型具有较强的去噪能力、编码简单、代码简洁、计算速度快、运行时间段等优点，可以通过分层抽象学习蛋白质对的有用特征，从数据中自动学习内部分布式特征表示。鉴于以上优点，DPPI模型可以作为蛋白互作预测的有益补充。