南水北调东线泵站机组站内叶片全调节优化研究

邵明猛

南水北调东线山东干线有限责任公司 山东济南 250013

泵站是南水北调工程的重要组成部分。而大型泵站大多是由多台水泵机组组成，运行时能耗较大，在实际运行中，若不采用变工况调节，仅在额定工况下运行，则泵站机组在大部分时间内未能在其效率较高的区间内运行，会造成电能的浪费，运行费用也将随之增加[1]。

1 问题研究

1.1 淮安四站机组情况

淮安四站是中国南水北调东线工程泵站之一，设有相同的立式轴流泵4台，其中包括3台常用机组，1台备用机组。泵站单台机组电机额定功率2500kW，机组扬程2-5m，设计工况4.18m。机组的叶片角度可调，调节范围是[-4°，+4°]，额定安放角为0°。Q-H采用二次多项式拟合，Q-η采用三次多项式拟合，Q为流速，H为扬程，η为水泵效率。Q-H关系曲线图如图1所示，Q-η关系曲线如图2所示。

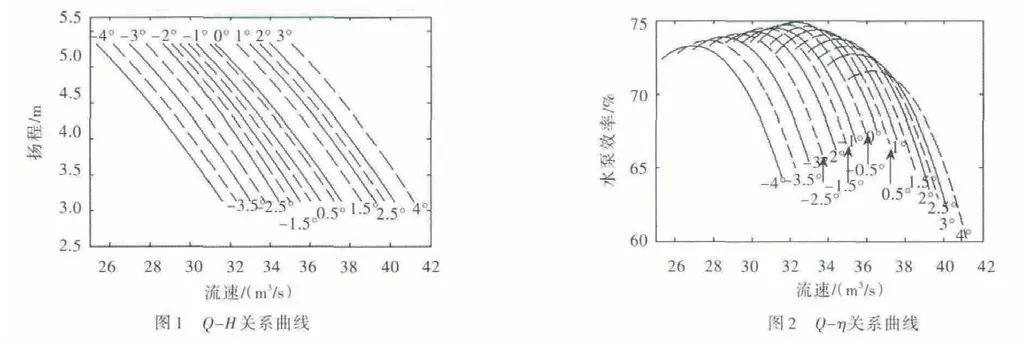
叶片角为额定安放角0°时，拟合结果如下：

大型泵站机组不宜频繁开机停机，因此以17∶00作为起始时刻，将全天分为12个时段，每个时段时长2h。

1.2 优化模型

泵站机组优化调度为满足日需水量的前提下，机组运行能耗费用最小。考虑到淮安四站有1台机组是备用机组，因此在该优化问题中只考虑3台机组。对应的数学模型如下：

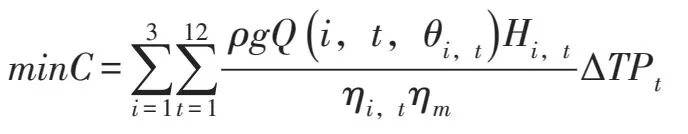
式中：i表示机组编号；t对应表1中的时段编号；ρ为水的密度；g为重力加速度；θi，t为时间段t内第i台机组的叶片角；Q（i，t，θi，t）为在时间段t内第i台机组叶片角为θi，t时的流量。叶片角的变化如图1所示。假设叶片角θ=-10表示机组停机状态，此时Q（i，t，-10）=0。ηi，t为第i台机组在时间段t时的水泵效率，ηm为电动机效率，当电机负荷大于60%时，可以认为效率保持在94%不变。△T为时段长度，Pt为时段t对应的电价。Hi，t为时间段t内第i台机组的扬程。

1.3 问题简化分析

泵站机组扬程主要取决于水渠每天的流入流出。淮安四站位于南水北调第二级泵站，水渠每天的流入流出基本维持平衡，可认为机组的扬程在一天中基本保持不变。在该问题研究中，扬程H选取每天的平均扬程Hav。为了减少计算量采用动态规划求解，并且不影响最后的结果，可以对泵站机组的流量作如下假设：

因此需求量约束条件为：

由于Qi≤QM，QM是泵站单台机组最大日流量，可对Qi的可行域如下分析：对于给定扬程H，每个时段包括停机在内共有S（S＜18）个不同的状态，包括S-1个可以调节的叶片角。全天划分为12个时间段，共有S12种组合。在不同的时间段内，即使叶片角一样，但由于电价不同，其费用也可能不同。因此要选择总费用最少的运行方式，机组要优先运行在电价最低的阶段。泵站单台机组在每个时间段内的总流量为Q（Si），i=1，2，…，S，S≤17。其中Q（S1）=0表示泵站机组关闭，此时S=1；S=2，3，…，17依次对应图1中[-4°，4°]中的叶片角。每一个QS值，对应着一个能耗，费用受能耗和分时电价影响。为了后续计算以及分析，可以将时间段顺序按照电价由低谷、平段、高峰排序。重新排序后的电价不影响最后的结果。后续分析如无特别说明，均采用重新排序后的时段编号。在上述假设的前提下，计算量的简化分为以下4个方面。

1.3.1 功率约束

在给定扬程H后，根据泵站机组性能拟合结果，计算出每个叶片角的泵站机组总流量和能耗以及功率。当功率不满足功率约束时，则后续计算均不考虑该叶片角。例如H=5.00m时，叶片角3°和4°的情形不满足要求，S=15，减少了两个不可能的状态[2]。

1.3.2 部分枚举法

枚举组合Sj∈N，j=1，2，…，12表示机组在时间段j的叶片角：Sj=1表示机组停机，Sj=2，3，…，17分别对应图1中的叶片角。泵站机组只在一个时间段内运行，则应在电价最低时刻运行，对应时段编号1。泵站机组在两个时间段内运行，则应在时段1和时段2内运行，组合情况满足如下条件：

2≤S1≤S，2≤S2≤S1，Sj=1，j=3，4，…，12

泵站机组在k个时间段内运行，则应在前k个时段运行，组合情况应该满足如下条件：

2≤S1≤S，2≤S2≤S1，…，2≤Sk≤Sk-1，Sj=1，j=k+1，k+2，…，12

基于如上分析，可以将原来的组合数目S12大大减少。当S=17时，采用上述分析法，组合情况有30421755，是1712的1（/1.9×107）。

1.3.3 组合的可行性判定

在上述枚举的组合中，组合对每种组合计算其日流量与对应的能耗费用组合（Q，C），并对计算结果进行可行性检查。QT、CT为符合规则的日流量序列以及其对应的费用序列，初始为空集。检查规则如下：针对QT-CT序列中的所有点，只要存在某点k使得其日流量大于Q且对应的能耗费用小于C，则该组合不可行，否则该组合满足可行性。当计算出的（Q，C）满足可行性时，将其存储入QT-CT序列，并删除原QT-CT序列中满足下述要求的点：某点其日流量小于Q，但其费用大于C。经过QT-CT算法处理后，其组合情况将大大较少，H=3.13m时，S=17，满足QT-CT条件的组合数目为3897，仅为枚举组合数量30421755的1（/7.7×103）。

1.3.4 单台机组提水量与需求量关系分析

日需水量QD满足如下要求QD≤3QM，QM为QT序列中最大值。考虑到0≤Q1≤Q2≤Q3，且Q1+Q2+Q3≥QD，可分为以下3种情形。

情形一：QD≤QM，则Q1、Q2、Q3应该满足如下条件：

情形二：QM＜QD≤2QM，则Q1、Q2、Q3应该满足如下条件：

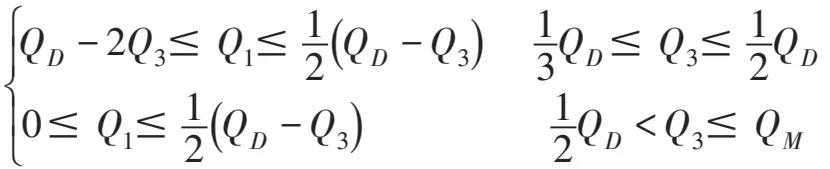
情形三：2QM＜QD≤3QM，则Q1、Q2、Q3应该满足如下条件：

1.4 算法实现

基于上述分析，设计出解决该问题的算法总体框架如图3所示。其中每一步详细算法如下所示：

（1）计算Qs、P。对于给定的日均扬程Hav以及文献中拟合的Q-H、η-Q关系，对于每个叶片角计算出对应时段的流量Qs，能耗P。其中Q（s1）=0，P（1）=0表示机组处于停机状态；Q（Si）、P（i），i≥2依次对应图1中的角度[-4°，+4°]。计算过程中把不满足功率要求的叶片角对应的数据从Qs、P序列中删除。计算公式如下：

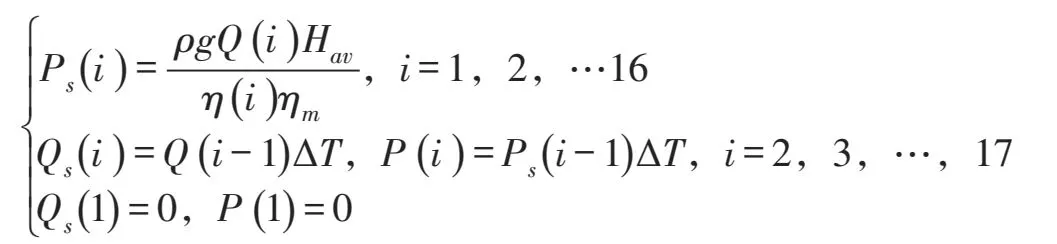
对应的功率约束：Ps（i）≤Pmax，i=1，2，…，16

（2）根据Q（Si）和P（i）序列计算QT-CT。

（3）根据前一小节Q1、Q2、Q3和QD关系，给定日需求量QD，采用动态规划求解Q1、Q2、Q3。

（4）输出控制序列。根据最优的（Q1、Q2、Q3）以及重新排序电价后的控制序列，输出正常时间顺序下的控制序列[3]。

2 结语

机组运行费用是泵站机组管理的重要标准之一。为了提高淮安四站的能源经济效率，在分时电价情况下，建立淮安四站3台机组叶片角全调节的优化调度数学模型。针对该模型特点，提出一种改进算法以减少计算量。